たとえば、有向グラフGを考えます。
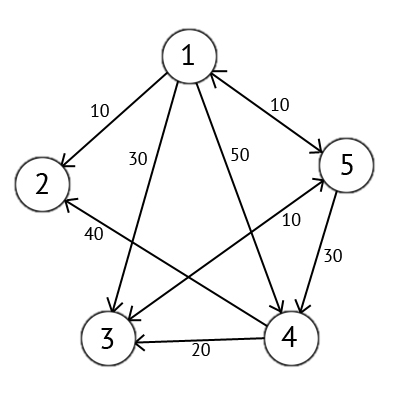
このグラフを行列Cの形式で表すことができます。
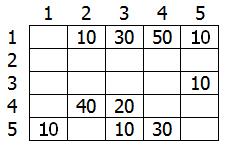
頂点1をソースとして使用すると、頂点1から頂点2、3、4、5までの最短ルートが検索されます。
このアルゴリズムは、グラフのすべての頂点を段階的に繰り返し、ラベルを割り当てます。ラベルは、ソース頂点から特定の頂点までの既知の最小距離です。 このアルゴリズムを例として考えてください。
この頂点がソースであるため、最初の頂点に0に等しいラベルを割り当てます。 残りの頂点には、無限に等しいラベルが割り当てられます。
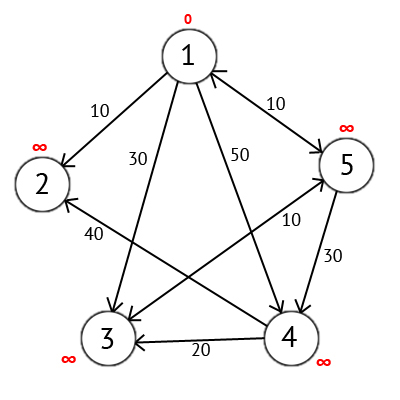
次に、最小ラベル(現在は頂点1)を持つ頂点Wを選択し、頂点Wから中間の頂点を含まないパスがあるすべての頂点を検討します。 取得した合計が前のラベル値よりも小さい場合にのみ、ラベルWと問題の頂点までのパスの長さの合計に等しいと見なされる各頂点にラベルを割り当てます。 量が少なくない場合は、前のラベルを変更しないでください。
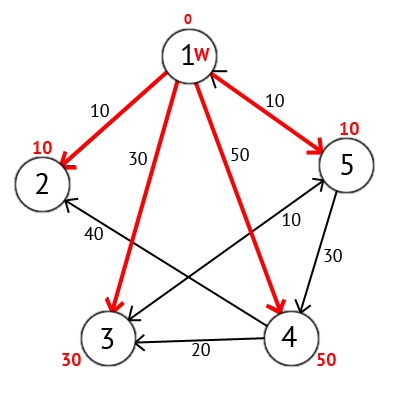
Wからの直接パスがあるすべての頂点を調べた後、頂点Wを訪問済みとしてマークし、最小ラベル値を持つ未訪問のものから選択します。次の頂点Wになります。この場合、これは頂点2です。または5.同じラベルの頂点が複数ある場合、どちらをWとして選択してもかまいません。
頂点2を選択します。ただし、そこから単一の出力パスはありません。そのため、この頂点をすぐに訪問済みとしてマークし、最小マークで次の頂点に移動します。 今回は、頂点5のみに最小ラベルがあります。 5本の直線があるが、まだ訪問済みとしてマークされていないすべてのピークを検討します。 繰り返しますが、頂点WのラベルとWから現在の頂点までのエッジの重みの合計を見つけ、この合計が前のラベルよりも小さい場合、ラベル値を受信した合計に置き換えます。
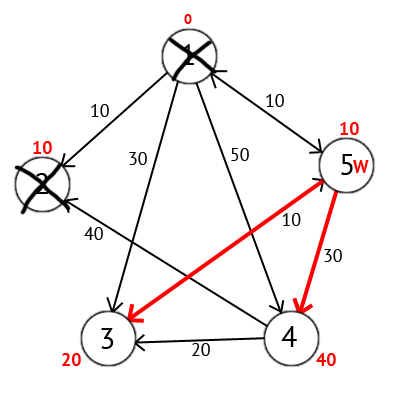
写真に基づいて、3番目と4番目のピークのラベルが小さくなったことがわかります。つまり、ソースの上部からこれらのピークへの短いルートが見つかりました。 次に、5番目の頂点を訪問済みとしてマークし、最小ラベルを持つ次の頂点を選択します。 未訪問のピークが現れるまで、上記のすべてのアクションを繰り返します。
すべてのアクションを完了すると、次の結果が得られます。
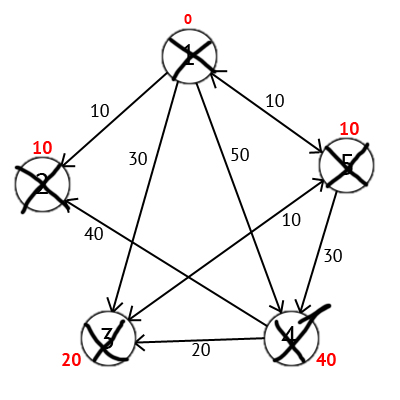
ベクトルPもあり、そこから最短ルートを構築できます。 要素の数だけ、このベクトルはグラフ内の頂点の数に等しくなり、各要素には、ソース頂点と最終頂点の間の最短パス上の最後の中間頂点が含まれます。 アルゴリズムの開始時に、ベクトルPのすべての要素はソースの頂点に等しくなります(この場合、P = {1、1、1、1、1})。 次に、検討中の頂点のラベル値を再計算する段階で、検討中の頂点のラベルがより小さいものに変更された場合、現在の頂点Wの値を配列Pに書き込みます。たとえば、3番目の頂点の値は30 さらに、W = 5で、3番目の頂点のラベルが「20」に変更されたため、値をベクトルP-P [3] = 5に書き込みます。 また、W = 5では、4番目の頂点のラベル値が変更され(「50」、「40」になった)、ベクトルPの4番目の要素をW-P [4] = 5に設定する必要があります。 その結果、ベクトルP = {1、1、5、5、1}が得られます。
ベクトルPの各要素で、最後の中間頂点がソースと最終頂点の間のパスに記録されることを知っているので、最短ルート自体を取得できます。