कैलटेक में साइनसोइडल मॉडलिंग और टाइपोस

यह पोस्ट लेख में वर्णित अपेक्षाकृत नई सिग्नल प्रोसेसिंग विधि के बारे में है जो कि विरल समय-आवृत्ति प्रतिनिधित्व के माध्यम से अनुकूली डेटा विश्लेषण , साथ ही साथ एक छोटी सी गलती है जो मुझे व्यक्तिगत रूप से भ्रमित करती है। यह लेख 2011 में कैलिफोर्निया इंस्टीट्यूट ऑफ टेक्नोलॉजी, थॉमस आई। होवे और शी ज़ॉत्ज़्यान में लागू गणित के प्रोफेसरों द्वारा प्रकाशित किया गया था, और, संभवत: जब आप इसे पढ़ते हैं, तब तक वे पहले ही इसे ठीक कर चुके होते हैं।

मैं इस लेख में गैर-रैखिक और गैर-स्थिर संकेतों के समय-आवृत्ति विश्लेषण के विभिन्न तरीकों की खोज में आया था - मेरे मामले में, मानव जहाजों में समान रक्त तत्वों को स्थानांतरित करने से अल्ट्रासोनिक संकेत। इस विश्लेषण का सार संकेत की विशेषताओं में परिवर्तन को ट्रैक करना है, दूसरे शब्दों में, हम समय पर संकेत की आवृत्तियों की निर्भरता जानना चाहते हैं। व्यापक तरीकों को छोड़कर - वर्णक्रमीय और तरंगिका विश्लेषण - EMD (अनुभवजन्य मोड में अपघटन) और साइनसोइडल मॉडलिंग जैसे तरीकों, जो बाद में चर्चा की जाएगी, पाए गए।

अनुभवजन्य विधियों की विधि उपयोग करने के लिए काफी सरल है, लेकिन यह विशेष रूप से परिणामों की वैधता के संदर्भ में विकसित नहीं है। थॉमस हो और शी ज़ुओक्यांग गणितीय तंत्र के विकास में आगे बढ़े और साइनसोइडल सिग्नल मॉडलिंग की अपनी पद्धति का प्रस्ताव रखा। उनका विचार सुगम आयामों के साथ हार्मोनिक्स में संकेत के अपघटन को विरल करना है। हम जो परिणाम प्राप्त करने की उम्मीद करते हैं वह ऊपर की तस्वीर में है। इस स्थिति में, फ़ंक्शन f (t) = 6t + cos (8 )t) + 0.5 cos (40 dect) द्वारा प्राप्त सिग्नल विघटित हो गया था। संकेत का अपघटन, ज़ाहिर है, अद्वितीय नहीं है, इसलिए, घटक हार्मोनिक्स की न्यूनतम की कसौटी पेश की गई थी, और समस्या निम्नानुसार बनाई गई थी:









P0 की समस्या का समाधान एम्पलीट्यूड ए और फेज फंक्शन थीटा के साथ सामंजस्य होगा, जिसका डेरिवेटिव सिग्नल फ्रिक्वेंसी के अनुरूप होगा। लेखक इस समस्या को पुनरावर्ती रूप से हल करने का प्रस्ताव देते हैं: हम एक हार्मोनिक घटक को निकालते हैं, हम शेष (माध्यिका) प्राप्त करते हैं - हम इसके साथ काम करते हैं, हम अगले हार्मोनिक को इसमें से निकालते हैं, हम शेष और इसी तरह प्राप्त करते हैं। चूंकि संकेत की तुलना में माध्य अधिक चिकना होना चाहिए, इसलिए हार्मोनिक ढूंढना निम्न समस्या को हल करने के लिए कम हो जाता है:







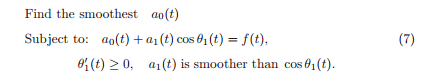
जहाँ a1 * cos (थीटा 1 (t)) प्राप्त हार्मोनिक है, a0 माध्यिका है। आयाम की चिकनाई कुल भिन्नता से निर्धारित होती है:









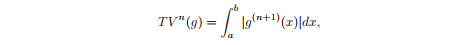
फ़ंक्शन जी की चिकनाई जितनी अधिक होगी, उसके शून्य (n + 1) व्युत्पन्न के करीब, तदनुसार, nth ऑर्डर की समग्र भिन्नता। हम यह भी कह सकते हैं: बहुपद का छोटा क्रम जिसके साथ हम प्रक्षेप कर सकते हैं, फ़ंक्शन को सुचारू कर सकते हैं। यह मानना ​​तर्कसंगत है कि कम से कम शून्य-क्रम भिन्नता की तलाश करना सबसे अच्छा है, हालांकि, इस मामले में हम एक टुकड़ा करने योग्य निरंतर कार्य (सीढ़ी प्रभाव) प्राप्त करने और उच्च आदेश की कुछ जानकारी खोने का जोखिम चलाते हैं जो हमें चाहिए (उदाहरण के लिए, वक्रता)। लेख के लेखकों ने तीसरे क्रम के बदलाव को कम करने का प्रस्ताव किया है, जो चौथे डेरिवेटिव को शून्य तक ले जाता है, जिससे क्यूबिक स्प्लिन द्वारा सन्निकटन के समान कुछ होता है। नतीजतन, हम मिनट टीवी ^ 3 (a0) की तलाश कर रहे हैं। लेकिन हमारे लिए यह भी महत्वपूर्ण है कि a1 पर्याप्त रूप से सुचारू है, इसलिए सर्वोत्तम स्थिति में, हमें min TV ^ 3 (a0) + मिनट λ * TV ^ 3 (a1) ढूंढना चाहिए, जहां λ लेगरेंज गुणक है, इस मामले में भार गुणांक की भूमिका निभाते हैं। । सरलता के लिए, लेखक λ = 1 को छोड़ कर निम्नलिखित समस्या पर पहुंचे:

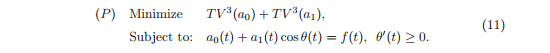
एल्गोरिथ्म

इस समस्या को हल करने के लिए एक पुनरावृत्ति एल्गोरिथ्म प्रस्तावित है। हालत में, एक और हार्मोनिक जोड़ा जाता है - बी 1 * पाप (थीटा 1 (टी)), इसकी चिकनाई भी हमारा लक्ष्य बन जाती है। हम चरण फ़ंक्शन थीटा ^ 0 को इस तरह से प्रारंभ करते हैं कि यह एक बढ़ती हुई क्रिया है जो कि स्थिति cos (थीटा ^ 0) = f (t) को संतुष्ट करती है, और मुख्य पुनरावृत्ति प्रारंभ करें:







पहले चरण में, हम समग्र आयाम भिन्नता को कम करते हैं। अगले पर - हम थीटा को उपरोक्त सूत्र के अनुसार अपडेट करते हैं, फिर जांचें कि यह कितना बदल गया है। एल्गोरिथ्म के अंत तक, यह माना जाता है कि आयाम बी 1 नगण्य होगा, तदनुसार, आर्टकग (बी 1 / ए 1) छोटा होगा, और थीटा कुछ मूल्य में परिवर्तित हो जाएगा। यह हमारा फेज फंक्शन होगा। थीटा ^ एन प्राप्त करने के बाद, हम पहले हार्मोनिक ए 1 * कॉस (थीटा 1 (टी)) को भेद करते हैं, जहां थीटा 1 = थीटा ^ एन। अगला, शेष पर इस एल्गोरिथ्म को चलाएं, अर्थात, हम मानों के साथ काम करते हैं f (t) = a0 + b1 * sin (theta1 (t))। निम्नलिखित हार्मोनिक a2 * cos (थीटा 2 (t)) का चयन करें, शेष के साथ जारी रखें। और इसलिए जब तक शेष का मान नगण्य है। मैंने पहला आदर्श लिया। उन लोगों के लिए जिन्हें इसकी परिभाषा याद नहीं है:









कुल भिन्नता को न्यूनतम खोजने की समस्या को लागू करने के लिए, लेखकों ने एल 1-न्यूनतमकरण की समस्या को कम किया, अंतर समीकरण को एक अंतर से बदल दिया। हमारे पास एक संकेत है, या एन बिंदुओं (नोड्स) का एक आदेशित सेट है जिसे हम विस्तार करना चाहते हैं, अर्थात, वैक्टर a0, a1 * cos (theta1 (t)) और b1 * sin (theta1 (t)) के योग के रूप में मौजूद है। और सुधार की समस्या में, एक दुर्भाग्यपूर्ण टाइपो देखा गया था:







मान लें कि a0 ^ n, a1 ^ n, b1 ^ n ग्रिड फ़ंक्शंस हैं, हम उनके चौथे डेरिवेटिव को मैट्रिक्स D ^ 4 द्वारा गुणा करके अनुमानित करते हैं। फिर, प्राप्त मूल्यों के मॉड्यूल के योग को कम करते हुए, हम संबंधित भिन्नताओं को कम करते हैं। सब कुछ तार्किक और विश्वसनीय है, लेकिन, इस एल्गोरिथ्म को लागू करने के बाद, मैं परिणामों को देखने के लिए भयभीत था - यह पूरी तरह से अराजक हो गया। लंबे समय तक कोड में एक त्रुटि खोजने की कोशिश करते हुए, मैंने अंततः महसूस किया कि त्रुटि लेख में थी।

तथ्य यह है कि Phi को x से गुणा करके हम एक वेक्टर प्राप्त करते हैं जहां तत्व a0 ^ n, a1 ^ n, b1 ^ n से संबंधित बिंदुओं पर व्युत्पन्न के योग हैं। यही है, हम तीन भिन्नताओं के योग के बजाय कुल भिन्नता (a0 ^ n + a1 ^ n + b1 ^ n) से घटाते हैं, जैसा कि ऊपर बताया गया है।

त्रुटि एक त्रुटि है, पाया गया, ठीक किया गया और कई महीनों तक भूल गया। और मई की छुट्टियों में, मैंने अभी भी प्रोफेसरों को एक पत्र लिखने के लिए एक प्रस्ताव के साथ लेख मिनट में बदलने के लिए तैयार किया। Phi * x || मिनट पर || D ^ 4 * a0 ^ n || + || D ^ 4 * a1 ^ n || + || D ^ 4 * b1 ^ n || हैरानी की बात है कि एक घंटे बाद प्रोफेसर हॉवे से एक जवाब आया, “आपके ईमेल के लिए धन्यवाद। हम आपके नोट का अध्ययन करेंगे और जल्द ही आपसे वापस मिलेंगे ”और एक सरल“ टॉम ”हस्ताक्षर के साथ।



एक और 6 घंटे के बाद, प्रोफेसर शी से एक पत्र आया:

प्रिय हांग्जो,



आपके ईमेल के लिए बहुत बहुत धन्यवाद। हमने यहां एक टाइपो बनाया।

\ Phi डायग (D4, D4, D4) होना चाहिए जो कि हम में भी इस्तेमाल किया गया था

एल्गोरिथ्म। धन्यवाद।



बेस्ट,

ज़ुओक्यांग शि

स्वाभाविक रूप से, मेरा संशोधन और जो वे लिखना चाहते थे, समान हैं। केवल एक चीज मुझे ध्यान देनी चाहिए कि यदि आप Phi मैट्रिक्स को इस धारणा के तहत स्टोर नहीं करते हैं कि यह विरल है, अर्थात, शून्य तत्वों का एक गुच्छा स्टोर करें, तो स्मृति जल्द ही समाप्त हो सकती है।

L1-न्यूनकरण समस्या को कैसे हल करें

उनके एल्गोरिथ्म के लिए, प्रोफेसरों ने विभाजन के तरीकों का प्रस्ताव किया है ब्रैगमैन पुनरावृत्ति और एल 1-नियमित-कम से कम वर्ग विधि। हालांकि, ये विधियां काफी हाल ही में हैं और शायद सभी पैकेज वायर्ड नहीं हैं। यह किसी के लिए भी उपयोगी है जो आलसी (मेरे जैसा) है, किसी भी एल्गोरिदम को लागू करने के लिए पहले मानदंड का न्यूनतम पता लगाने के लिए कि यह समस्या अधिक सामान्य रैखिक प्रोग्रामिंग समस्या को कैसे कम करती है। मूल कार्य इस प्रकार है:









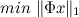
के अधीन है







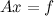
जहां A मैट्रिक्स NxM है, Phi मैट्रिक्स KxM है, x आयाम M का वेक्टर है।



यह निम्नलिखित रैखिक प्रोग्रामिंग कार्य के बराबर है:









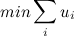
शर्तों के तहत



















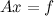
जहां phi (i, j) मैट्रिक्स Phi के तत्व हैं।



औपचारिक रूप से, संक्रमण निम्नानुसार किया जा सकता है। K वैरिएबल को वेक्टर x में जोड़ा जाता है, जिससे यह आयाम बन जाता है K + M:







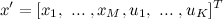
मैट्रिक्स A के आयाम NxK को मैट्रिक्स A में जोड़ा जाता है:









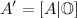
वेक्टर सी (एलपी समस्या में गुणांक) में एम शून्य और के इकाइयां शामिल हैं:









मैट्रिक्स F मैट्रिक्स Phi और पहचान मैट्रिक्स I से बना है। आयाम F - (2 * K) x (M + K):











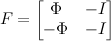
इस प्रकार, एक औपचारिक कार्य इस तरह दिखता है:







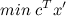
शर्तों के तहत

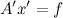
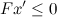
परिणाम

यहाँ पहले से वर्णित उदाहरण f (t) = 6t + cos (8πt) + 0.5 cos (40 )t) के लिए एल्गोरिथ्म के परिणाम दिए गए हैं। रेखांकन में, इस एल्गोरिथ्म (नीला) द्वारा प्राप्त मूल्यों की तुलना विश्लेषणात्मक मूल्यों (लाल) और अनुभवजन्य मोड (काला) में विघटित करके प्राप्त मूल्यों के साथ की जाती है।







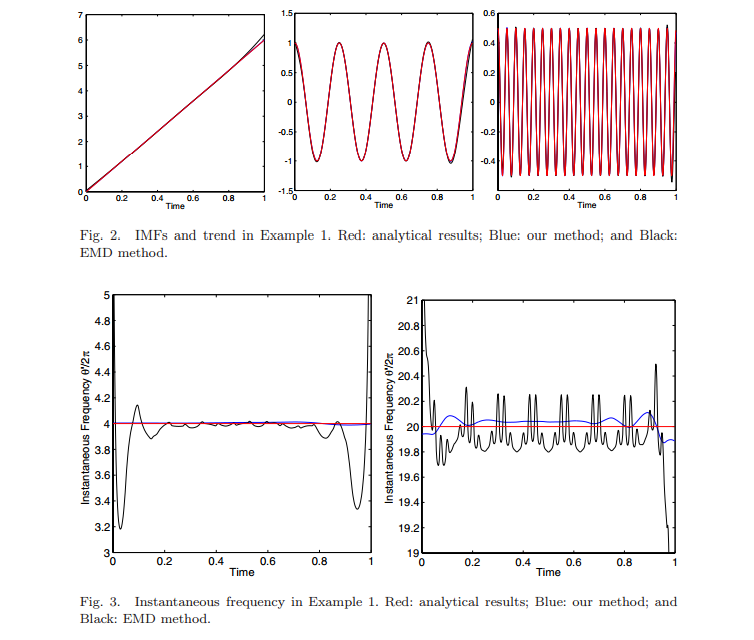
निम्न उदाहरण दिखाता है कि यह विधि सिग्नल में आवृत्ति परिवर्तनों को ट्रैक करने में कैसे मदद करती है।















अन्य उदाहरण लेख में इंगित किए गए हैं, साथ ही साथ वास्तविक डेटा पर काम करने वाले एल्गोरिदम के परिणाम भी।

परिणाम

एल्गोरिथ्म बहुत दिलचस्प है और, मेरी राय में, आगे के विश्लेषण की आवश्यकता है, क्योंकि यहां विचार के लिए बहुत जगह है। इसके स्पष्ट नुकसान महान कम्प्यूटेशनल जटिलता हैं, साथ ही शोर के प्रति संवेदनशीलता और, परिणामस्वरूप, शोर डेटा के साथ अस्थिर संचालन। लेखक लो-पास फ़िल्टरिंग और फूरियर रूपांतरण का उपयोग करके संवेदनशीलता समस्या को हल करने का प्रस्ताव करते हैं। लेकिन उस समय के बारे में अधिक।

अंत में, मैं एक बार फिर से घमंड करना चाहूंगा और कहना चाहूंगा कि, जाहिर है, यह भी होता है कि कालटेक में प्रोफेसर बेहूदा, गलतियां करते हैं, और एक रूसी छात्र जिनके पास अभी तक कुंवारा नहीं है, वे उन्हें इस ओर इशारा कर सकते हैं।