
The number of more or less different sorts from each other is guaranteed to be more than a hundred. Among them there are subgroups of algorithms that are minimally different from each other, coinciding in some general main idea. In fact, in different years, different people come up with the same sortings anew, differing in not very fundamental details.
Such an algorithmic idea is found more often than others.
Each element is entered approximately in that place of the array where it should be located. It turns out an almost ordered array. To which sorting by inserts is applied (it is most effective for processing almost ordered arrays) or local unordered areas are processed recursively by the same algorithm.
To estimate approximately where you want to put the element, you need to find out how much it differs from the average element of the array. To do this, you need to know the values of the minimum and maximum elements, well, and the size of the array.
This article was written with the support of EDISON Software, which develops a wide range of solutions for a variety of tasks: from programs for online trying on multi-brand clothing stores to LED transmission systems between river and sea vessels .
We love the theory of algorithms! ;-)
The sorted array is supposed to have really random data. All inventors of this method come to the same formula:
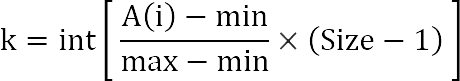
k is the approximate place in the array where the element A ( i ) should be
min , max - values of the minimum and maximum elements in array A
Size - the number of elements in array A
Here is such a general idea. Let's see in what variations this algorithm was born again and again.
Sorting King Solomon :: Solomon sort

This method (and its beautiful name) was proposed by the user of V2008n about 5 years ago. Everything has its time, “the time to scatter stones and the time to collect stones” (the words of King Solomon from the book of Ecclesiastes) - and in the algorithm, this is exactly what happens. First, with the help of the formula, we scatter the elements at the desired places in the array. Since the formula gives not an exact, but an approximate place, several elements that are close to each other in value pretend to some positions at once. These local element groups are sorted by inserts and then assembled in the final order.
Interpolation sort
“There is nothing new under the sun,” to quote the same author again. Wikipedia describes sorting by interpolation, suspiciously reminiscent of Solomon sorting. Each “pile of stones” is a small additional dynamic array, where elements of similar importance are located. The main difference is that after “scattering stones”, these local unsorted groups of elements are sorted not by inserts, but by sorting themselves by interpolation (recursively or in a loop).
An ordered array is a discrete data set that can be considered as a finite set of known values of a certain unknown function. Actually, the approximate distribution from the point of view of computational mathematics - this is interpolation.
JavaScript Interpolation Sort - Loopback
Array.prototype.interpolationSort = function() { var divideSize = new Array(); var end = this.length; divideSize[0] = end; while(divideSize.length > 0) {divide(this);} function divide(A) { var size = divideSize.pop(); var start = end - size; var min = A[start]; var max = A[start]; var temp = 0; for(var i = start + 1; i < end; i++) { if(A[i] < min) { min = A[i]; } else { if(A[i] > max) {max = A[i];} } } if(min == max) { end = end - size; } else { var p = 0; var bucket = new Array(size); for(var i = 0; i < size; i++) {bucket[i] = new Array();} for(var i = start; i < end; i++) { p = Math.floor(((A[i] - min) / (max - min)) * (size - 1)); bucket[p].push(A[i]); } for(var i = 0; i < size; i++) { if(bucket[i].length > 0) { for(var j = 0; j < bucket[i].length; j++) {A[start++] = bucket[i][j];} divideSize.push(bucket[i].length); } } } } };
JavaScript interpolation sort - recursive version
Array.prototype.bucketSort = function() { var start = 0; var size = this.length; var min = this[0]; var max = this[0]; for(var i = 1; i < size; i++) { if (this[i] < min) { min = this[i]; } else { if(this[i] > max) {max = this[i];} } } if(min != max) { var bucket = new Array(size); for(var i = 0; i < size; i++) {bucket[i] = new Array();} var interpolation = 0; for(var i = 0; i < size; i++){ interpolation = Math.floor(((this[i] - min) / (max - min)) * (size - 1)); bucket[interpolation].push(this[i]); } for(var i = 0; i < size; i++) { if(bucket[i].length > 1) {bucket[i].bucketSort();} //Recursion for(var j = 0; j < bucket[i].length; j++) {this[start++] = bucket[i][j];} } } };
Histogram sort :: Histogram sort
This is an optimization of sorting by interpolation, which counts the number of elements belonging to local unsorted groups. This count allows you to insert unsorted items directly into the resulting array (instead of grouping them into separate small arrays).
JavaScript Bar Sort
Array.prototype.histogramSort = function() { var end = this.length; var sortedArray = new Array(end); var interpolation = new Array(end); var hitCount = new Array(end); var divideSize = new Array(); divideSize[0] = end; while(divideSize.length > 0) {distribute(this);} function distribute(A) { var size = divideSize.pop(); var start = end - size; var min = A[start]; var max = A[start]; for(var i = start + 1; i < end; i++) { if (A[i] < min) { min = A[i]; } else { if (A[i] > max) {max = A[i];} } } if (min == max) { end = end - size; } else { for(var i = start; i < end; i++){hitCount[i] = 0;} for(var i = start; i < end; i++) { interpolation[i] = start + Math.floor(((A[i] - min) / (max - min)) * (size - 1)); hitCount[interpolation[i]]++; } for(var i = start; i < end; i++) { if(hitCount[i] > 0){divideSize.push(hitCount[i]);} } hitCount[end - 1] = end - hitCount[end - 1]; for(var i = end - 1; i > start; i--) { hitCount[i - 1] = hitCount[i] - hitCount[i - 1]; } for(var i = start; i < end; i++) { sortedArray[hitCount[interpolation[i]]] = A[i]; hitCount[interpolation[i]]++; } for(var i = start; i < end; i++) {A[i] = sortedArray[i];} } } };
Interpolation tag sort
In order to further optimize the overhead, it is proposed here to remember not the number of similar elements in unsorted groups, but simply mark the beginning of these groups with True / False flags. True means that the subgroup is already sorted, and False means that it is not yet.
JavaScript tagged interpolation sort
Array.prototype.InterpolaionTagSort = function() { var end = this.length; if(end > 1) { var start = 0 ; var Tag = new Array(end); //Algorithm step-1 for(var i = 0; i < end; i++) {Tag[i] = false;} Divide(this); } //Algorithm step-2 while(end > 1) { while(Tag[--start] == false){} //Find the next bucket's start Divide(this); } function Divide(A) { var min = A[start]; var max = A[start]; for(var i = start + 1; i < end; i++) { if(A[i] < min) { min = A[i]; } else { if(A[i] > max ) {max = A[i];} } } if(min == max) { end = start; } else { //Algorithm step-3 Start to be the next bucket's end var interpolation = 0; var size = end - start; var Bucket = new Array(size);//Algorithm step-4 for(var i = 0; i < size; i++) {Bucket[i] = new Array();} for(var i = start; i < end; i++) { interpolation = Math.floor(((A[i] - min) / (max - min)) * (size - 1)); Bucket[interpolation].push(A[i]); } for(var i = 0; i < size; i++) { if(Bucket[i].length > 0) {//Algorithm step-5 Tag[start] = true; for(var j = 0; j < Bucket[i].length; j++) {A[start++] = Bucket[i][j];} } } } }//Algorithm step-6 };
Interpolation tag sort (in-place)
If the values of the elements in the array are not repeated and evenly distributed (roughly speaking - if the data in sorted form is something like an arithmetic progression), then you can sort in one pass, sorting right in place, without moving the elements to intermediate arrays.
Sort by interpolation with labels (in place) in JavaScript
Array.prototype.InPlaceTagSort = function() { var n = this.length; var Tag = new Array(n); for(i = 0; i < n; i++) {Tag[i] = false;} var min = this[0]; var max = this[0]; for(i = 1; i < n; i++) { if(this[i] < min) { min = this[i]; } else { if(this[i] > max) {max = this[i];} } } var p = 0; var temp = 0; for(i = 0; i < n; i++) { while(Tag[i] == false) { p = Math.floor(((this[i] - min) / (max - min)) * (n - 1)); temp = this[i]; this[i] = this[p]; this[p] = temp; Tag[p] = true; } } };
Flash Sort :: Flashsort
Once upon a time, I wrote about sorting, which was invented by professor of biophysics Neubert in 1998.
The professor suggested distributing the elements into several separate classes (class membership is determined by the size of the element). With this in mind, the formula looks like this:
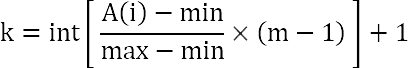
Instead of Size (array size), the formula indicates m - the number of classes by which we distribute the elements of the array. The formula does not calculate the key in the array where the element should be thrown, but the class number to which the element belongs.
This sorting is not bad in that it is more economical about additional memory. The redistribution of elements occurs in place. Only localization of classes is stored separately (well, if you look from a different angle, the number of elements belonging to a particular class is stored separately).
Well, the rest is the same song.
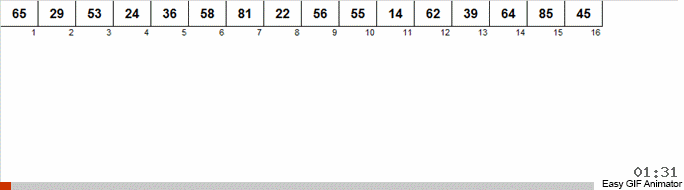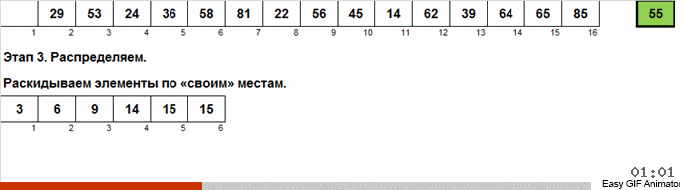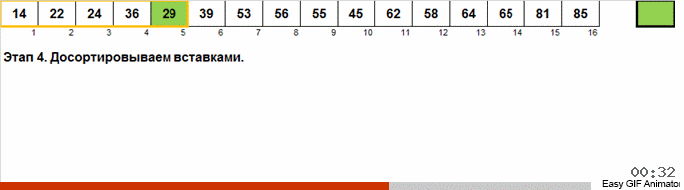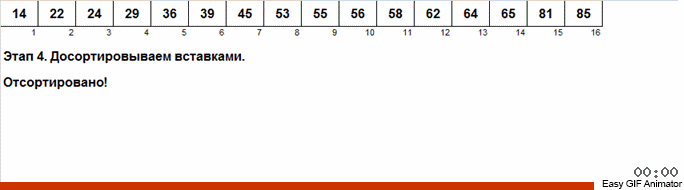
Flash Sort in Java
/** * FlashSort.java - integer version * Translation of Karl-Dietrich Neubert's algorithm into Java by * Rosanne Zhang */ class FlashSort { static int n; static int m; static int[] a; static int[] l; /* constructor @param size of the array to be sorted */ public static void flashSort(int size) { n = size; generateRandomArray(); long start = System.currentTimeMillis(); partialFlashSort(); long mid = System.currentTimeMillis(); insertionSort(); long end = System.currentTimeMillis(); // print the time result System.out.println("Partial flash sort time : " + (mid - start)); System.out.println("Straight insertion sort time: " + (end - mid)); } /* Entry point */ public static void main(String[] args) { int size = 0; if (args.length == 0) { usage(); System.exit(1); } try { size = Integer.parseInt(args[0]); } catch (NumberFormatException nfe) { usage(); System.exit(1); } FlashSort.flashSort(size); } /* Print usage */ private static void usage() { System.out.println(); System.out.println("Usage: java FlashSort n "); System.out.println(" n is size of array to sort"); } /* Generate the random array */ private static void generateRandomArray() { a = new int[n]; for(int i=0; i < n; i++) { a[i] = (int)(Math.random() * 5 * n); } m = n / 20; l = new int[m]; } /* Partial flash sort */ private static void partialFlashSort() { int i = 0, j = 0, k = 0; int anmin = a[0]; int nmax = 0; for(i=1; i < n; i++) { if (a[i] < anmin) anmin=a[i]; if (a[i] > a[nmax]) nmax=i; } if(anmin == a[nmax]) return; double c1 = ((double)m - 1) / (a[nmax] - anmin); for(i=0; i < n; i++) { k= (int) (c1 * (a[i] - anmin)); l[k]++; } for(k=1; k < m; k++) { l[k] += l[k - 1]; } int hold = a[nmax]; a[nmax] = a[0]; a[0] = hold; int nmove = 0; int flash; j = 0; k = m - 1; while(nmove < n - 1) { while(j > (l[k] - 1)) { j++; k = (int) (c1 * (a[j] - anmin)); } flash = a[j]; while(!(j == l[k])) { k = (int) (c1 * (flash - anmin)); hold = a[l[k] - 1]; a[l[k] - 1] = flash; flash = hold; l[k]--; nmove++; } } } /* Straight insertion sort */ private static void insertionSort() { int i, j, hold; for(i = a.length - 3; i >= 0; i--) { if(a[i + 1] < a[i]) { hold = a[i]; j = i; while (a[j + 1] < hold) { a[j] = a[j + 1]; j++; } a[j] = hold; } } } /* For checking sorting result and the distribution */ private static void printArray(int[] ary) { for(int i=0; i < ary.length; i++) { if((i + 1) % 10 ==0) { System.out.println(ary[i]); } else { System.out.print(ary[i] + " "); } System.out.println(); } } }
Approximate Sort :: Proxmap sort
This sort is the oldest of those mentioned here, it was introduced in 1980 by Professor Thomas Standish of the University of California. In appearance, it seems to be significantly different, but if you look closely, everything is the same.
The algorithm operates with such a concept as a hit - a certain number that is close in value to some element of the array.
To determine whether an array element is a hit, an approximating function is applied to the element.
Professor Standish sorted arrays of real numbers. The approximating function was to round down the real numbers down to an integer.
That is, for example, if the array contains elements 2.8, 2, 2.1, 2.6, etc. then a hit for these numbers will be deuce.

General procedure:
- We apply an approximating function to each element, determining which hit corresponds to the next element.
- Thus, for each hit, we can calculate the number of elements corresponding to this hit.
- Knowing the number of elements for all hits, we determine the localization of hits (borders on the left) in the array.
- Knowing the localization of hits, we determine the localization of each element.
- Having determined the localization of the element, we try to insert it in its place in the array. If the place is already taken, then we move the neighbors to the right (if the element is smaller than them) to make room for the element. Or to the right we insert the element itself (if it is more than neighbors).
As an approximating function, you can assign any one based on the general nature of the data in the array. In modern implementations of this sorting, hits are usually determined not by nibbling off the fractional part, but using our favorite formula.
JavaScript approximation sort
Array.prototype.ProxmapSort = function() { var start = 0; var end = this.length; var A2 = new Array(end); var MapKey = new Array(end); var hitCount = new Array(end); for(var i = start; i < end; i++) {hitCount[i] = 0;} var min = this[start]; var max = this[start]; for (var i = start+1; i < end; i++){ if (this[i] < min) { min = this[i]; } else { if(this[i] > max) {max = this[i];} } } //Optimization 1.Save the MapKey[i]. for (var i = start; i < end; i++) { MapKey[i] = Math.floor(((this[i] - min ) / (max - min)) * (end - 1)); hitCount[MapKey[i]]++; } //Optimization 2.ProxMaps store in the hitCount. hitCount[end-1] = end - hitCount[end - 1]; for(var i = end-1; i > start; i--){ hitCount[i-1] = hitCount[i] - hitCount[i - 1]; } //insert A[i]=this[i] to A2 correct position var insertIndex = 0; var insertStart = 0; for(var i = start; i < end; i++){ insertIndex = hitCount[MapKey[i]]; insertStart = insertIndex; while(A2[insertIndex] != null) {insertIndex++;} while(insertIndex > insertStart && this[i] < A2[insertIndex - 1]) { A2[insertIndex] = A2[insertIndex - 1]; insertIndex--; } A2[insertIndex] = this[i]; } for(var i = start; i < end; i++) {this[i] = A2[i];} };
Hash sort insertion sorting :: Hash sort
Well, we finish our review with the algorithm that the bobbyKdas habraiser suggested 6 years ago. This is a hybrid algorithm in which, in addition to distribution and insertions, merging is also added.
- The array is recursively divided in half, until at some step the sizes of the half-subarrays reach the minimum size (the author has no more than 500 elements).
- At the lowest level of recursion, a familiar algorithm is applied to each half-subarray - using the same formula, an approximate distribution occurs inside the subarray, with sorting by inserts of local unsorted sections.
- After ordering the two halves of the subarrays, they merge.
- Point 3 (merging of sorted halves of subarrays) is repeated when lifting along recursion levels to the very top, when the original array is combined from two halves.
Sort by hash insertion in Java
import java.util.Arrays; import java.util.Date; import java.util.Random; public class HashSort { // static int SOURCELEN = 1000000; int source[] = new int[SOURCELEN]; // int quick[] = new int[SOURCELEN]; // static int SORTBLOCK = 500; static int k = 3; // static int TMPLEN = (SOURCELEN < SORTBLOCK * k) ? SORTBLOCK * k : SOURCELEN; int tmp[] = new int[TMPLEN]; // static int MIN_VAL = 10; static int MAX_VAL = 1000000; int minValue = 0; int maxValue = 0; double hashKoef = 0; // public void randomize() { int i; Random rnd = new Random(); for(i=0; i<SOURCELEN; i++) { int rndValue = MIN_VAL + ((int)(rnd.nextDouble()*((double)MAX_VAL-MIN_VAL))); source[i] = rndValue; } } // - public void findMinMax(int startIndex, int endIndex) { int i; minValue = source[startIndex]; maxValue = source[startIndex]; for(i=startIndex+1; i<=endIndex; i++) { if( source[i] > maxValue) { maxValue = source[i]; } if( source[i] < minValue) { minValue = source[i]; } } hashKoef = ((double)(k-1)*0.9)*((double)(endIndex-startIndex)/((double)maxValue-(double)minValue)); } // ( - ) public void stickParts(int startIndex, int mediana, int endIndex) { int i=startIndex; int j=mediana+1; int k=0; // - while(i<=mediana && j<=endIndex) { if(source[i]<source[j]) { tmp[k] = source[i]; i++; } else { tmp[k] = source[j]; j++; } k++; } // - if( i>mediana ) { while(j<=endIndex) { tmp[k] = source[j]; j++; k++; } } // - if(j>endIndex) { while(i<=mediana) { tmp[k] = source[i]; i++; k++; } } System.arraycopy(tmp, 0, source, startIndex, endIndex-startIndex+1); } // // boolean shiftRight(int index) { int endpos = index; while( tmp[endpos] != 0) { endpos++; if(endpos == TMPLEN) return false; } while(endpos != index ) { tmp[endpos] = tmp[endpos-1]; endpos--; } tmp[endpos] = 0; return true; } //- public int hash(int value) { return (int)(((double)value - (double)minValue)*hashKoef); } // public void insertValue(int index, int value) { int _index = index; // , // - while(tmp[_index] != 0 && tmp[_index] <= value) { _index++; } // , if( tmp[_index] != 0) { shiftRight(_index);// } tmp[_index] = value;// - } // public void extract(int startIndex, int endIndex) { int j=startIndex; for(int i=0; i<(SORTBLOCK*k); i++) { if(tmp[i] != 0) { source[j] = tmp[i]; j++; } } } // public void clearTMP() { if( tmp.length < SORTBLOCK*k) { Arrays.fill(tmp, 0); } else { Arrays.fill(tmp, 0, SORTBLOCK*k, 0); } } // public void hashingSort(int startIndex, int endIndex) { //1. findMinMax(startIndex, endIndex); //2. clearTMP(); //3. - for(int i=startIndex; i<=endIndex; i++) { insertValue(hash(source[i]), source[i]); } //4. extract(startIndex, endIndex); } // public void sortPart(int startIndex, int endIndex) { // 500, - if((endIndex - startIndex) <= SORTBLOCK ) { hashingSort(startIndex, endIndex); return; } // > 500 int mediana = startIndex + (endIndex - startIndex) / 2; sortPart(startIndex, mediana);// sortPart(mediana+1, endIndex);// stickParts(startIndex, mediana, endIndex);// - } // public void sort() { sortPart(0, SOURCELEN-1); } public static void main(String[] args) { HashSort hs = new HashSort(); hs.randomize(); hs.sort(); } }
The formula itself is called a hash function, and the auxiliary array for approximate distribution is called a hash table.
References
 Interpolation & Histogram , Flash , Proxmap
Interpolation & Histogram , Flash , Proxmap
 Solomon , Hash Table , Flash
Solomon , Hash Table , Flash
Series Articles:
- Excel application AlgoLab.xlsm
- Exchange Sorts
- Insertion Sorts
- Sort by selection
- Merge Sorts
- Sort by distribution
- Counting sorts with approximate distribution
- American Flag Sort
- Suffix tree in bitwise sorting
- Comparing Distribution Sorts