The Russian edition of the Guide to Competitive Programming (Springer International Publishing AG) was published with the support of the Moscow Institute of Physics and Technology and its head Alexei Maleev, Mail.Ru Group, as well as the Moscow Workshops ICPC project.

“Olympiad programming is becoming more and more popular every year among students and students. An excellent example of this was the fact that in 2019, we, the Moscow Workshops ICPC, in November we will hold the tenth training camp preparations for the World Cup in various parts of the globe, they have already passed in Singapore, and Europe and South America, and Russia - from Vladivostok to Moscow. At the beginning of October, the Moscow Programming Contest took place in Moscow, in which 2284 people took part at 18 venues of Moscow universities - this is an absolute record for the scale of the competition, which was held with the support of Rosmolodezh.“Guide to Competitive Programming” was translated into Russian from English. In addition to English and Russian, the publication in Korean was released.
We are very happy about the lively interest of the guys, and are ready to support it in every way - for example, for students of Moscow universities we conduct free training for ICPC with the participation of the best trainers. And, of course, consolidating the material, disassembling the tasks, and drawing up their knowledge to the participants is always useful. Therefore, I am very glad that your book has appeared, and I congratulate all of us on this. We hope that at the ICPC finals in Moscow in June 2020 there will already be those guys who read it and become the heroes of the second, supplemented edition. ”
Alexey Maleev, Director of the final of the ICPC 2020 World Championship in Moscow, Vice-Rector of MIPT, founder of the Moscow Workshops ICPC project.
The author of the book is Antti Laaxsonen, a teacher and researcher from the University of Helsinki Aalto (Finland) [3] with extensive experience in teaching programming and algorithms, and the coach of the Finland team at international programming competitions. He has a high rating of 2347 and the status of “international master” on the Codeforces portal under the nickname “pllk” [4]. In 2008, he A. Laaxsonen became one of the organizers of the Informatics Olympiad in his country. In 2016 - scientific supervisor of the Baltic Olympiad in Informatics.
The target audience of the book are all interested and / or working in the field of Olympiad programming. But, for the full assimilation of the material, knowledge of the basics of programming is required, while the author does not require the reader to have experience in designing algorithms or participating in competitions. All this allows us to recommend this work to a wide range of interested readers. For beginners, it will become an introduction to modern olympiad programming, experienced specialists will help to systematize knowledge, will become a reference tool for them.
Submission of material in the book is carried out from simple to complex. At first he gets acquainted with the goals and objectives of the book, with the Olympiad programming, the collection of tasks CSES [5] and other relevant books on Olympiad programming.
Having received the necessary theoretical base, the reader will be ready to move on to practice. Programming technique is the next topic. In it, the author included the basics of the C ++ language (C11 standard), which implements all the examples in the book; analysis of recursive algorithms and bitwise operations.
In the chapters of the book, the reader will be able to find information on most of the “standard” topics and examples of implementation of algorithms that are offered to participants in programming olympiads: data structures, dynamic programming, graph algorithms and tree algorithms, range queries, and work with strings.
Separately, I would like to highlight a number of chapters of the book. For example, the chapter “Selected Design Issues for Algorithms”. It included algorithms with parallel viewing of discharges, depreciation analysis, and finding the minimum values. The reader is offered algorithms for finding the Hamming distance, the solution of the reachability problem in graphs, the two-pointer method, ternary search, minimization of sums and other interesting topics for the “Olympiad” and their trainers.
As an example, I will give an example of tasks from the chapter “Selected questions of designing algorithms”.
Let's consider algorithms with parallel viewing of digits in which bitwise operations are used for efficient data processing. In a typical case, we can replace the for loop with bitwise operations, which significantly reduces the running time of the algorithm.
Parallel Browsing Algorithms
Algorithms with parallel viewing of digits are based on the fact that individual digits of a number can be manipulated in parallel using bitwise operations. Therefore, one of the methods for designing algorithms is to present the steps of the algorithm in such a way that they can be effectively implemented using bitwise operations.
Hamming Distance Hamming Distance
hamming (a, b) between lines a and b of the same length is the number of positions at which these lines differ. For example:
hamming (01101, 11001) = 2.
Consider the following task: given n bit strings of length k, calculate the minimum Hamming distance between two strings. For example, for lines [00111, 01101, 11110], the answer is 2, because
- hamming (00111, 01101) = 2;
- hamming (00111, 11110) = 3;
- hamming (01101, 11110) = 3.
The problem can be solved “head-on” by calculating the Hamming distance between every two lines. The time complexity of such an algorithm is (n
k). To calculate the distance between lines a and b, use the following function:
int hamming(string a, string b) { int d = 0 for (int i = 0; i < k; i++) { if (a[i] != b[i]) d++; } return d; }
But since the strings consist of bits, the solution can be optimized by storing the strings as integers and calculating the distance between them using bitwise operations. In particular, if k ≤ 32, then the strings can be stored as int values and to calculate the distance use this function:
int hamming(int a, int b) { return __builtin_popcount(a^b); }
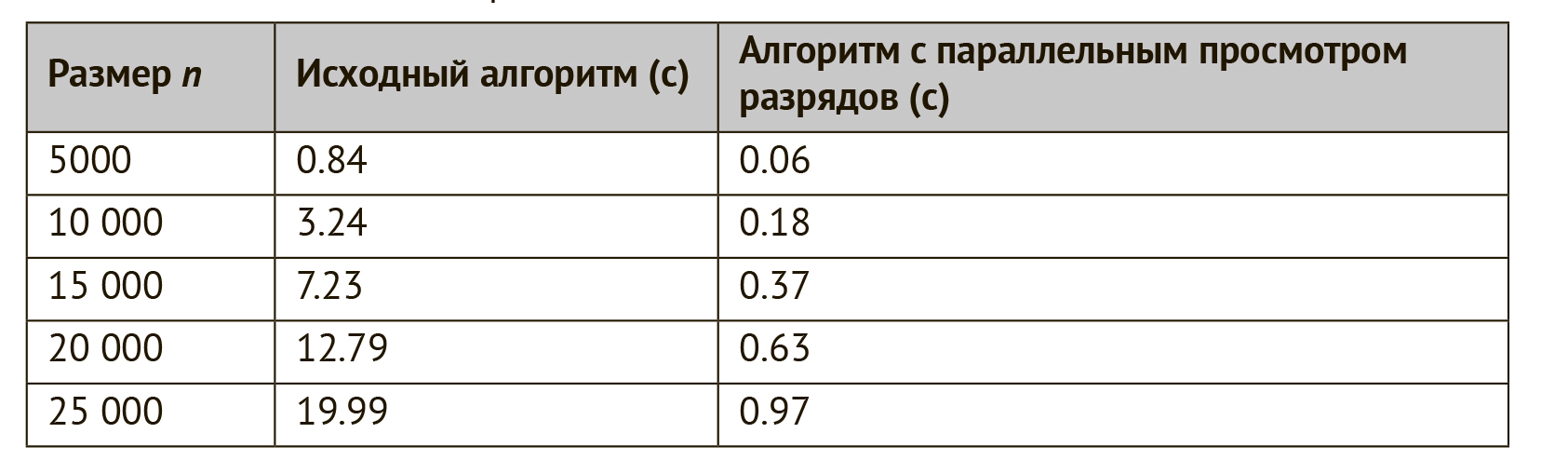
Here the EXCLUSIVE OR operation builds a line in which the units are in those positions where a and b differ. Then the number of unit digits is calculated by the __builtin_popcount function. The table shows the results of comparing the original algorithm and the algorithm with a parallel view of the bits in terms of run time on a modern computer. The algorithm with parallel viewing of bits turned out to be about 20 times faster.
Table: Running time of algorithms calculating the minimum Hamming distance for n bit strings of length k = 30
The chapters “Mathematics” and “Geometry” deserve no less attention. As the reader already guessed, they are devoted to solving mathematical and geometric problems by means of the C ++ programming language and the construction of appropriate algorithms. In the “mathematical” chapter, five big topics await us: “Number Theory”, “Combinatorics”, “Matrices”, “Probability” and “Game Theory”. And in the “geometric”: “Technical means in geometry”, “Algorithms based on the sweeping line”. Thus, the complex presentation of the construction of algorithms for solving mathematical and geometric problems makes the book a “find” for the “olympiadniki”, because against the background of a shortage of books on this subject, this is a rarity.
A number of problems, the author decided to put in the chapter “Additional topics”. Their development “sometimes can help in solving the most difficult olympiad problems”. This is “The square root in the algorithms”, “And again about the segment trees”, “Duchi”, “Optimization of dynamic programming” and “Miscellaneous”. Proceeding from the name of the additional explanation, they require subheading about trees of segments and about different things.
As for the trees of segments, the reader will get acquainted with lazy propagation, dynamic trees, data structures at the vertices, two-dimensional trees. And in “Miscellaneous” he is waiting for: a meeting in the middle (dividing the search space into two parts, approximately equal, performing a search in each part, and then combining the results), counting sets, parallel binary search, dynamic connectivity.
Complete the book reference information on mathematics and an extensive bibliography (32 sources).
So, the book “Olympiad programming” by Antti Laaxsonen is an excellent introduction to the world of sports programming. At the same time, a wonderful reference guide. The book is suitable for beginners "olympiadnikov" and will help in organizing knowledge experienced. It will be useful for coaches.
Once again, we note that all the examples in the book are implemented in the C ++ programming language. He is most in demand at the Olympics. But someone may find this a drawback of the book, because other languages are popular - Python, Java. Those who prefer these programming languages can solve the proposed problems in a book in their favorite language. This will be a good workout. Ultimately, it is precisely in the search for the optimal solution that the Olympiad tasks are completed.
The article was prepared by: Igor Shtompel, author and presenter of the section "Career \ Education" in the journal "System Administrator"