Recently, the ranges that should be included in the C ++ 20 standard have been discussed quite a lot, including on Habré ( an example where there are many examples ). There are enough critics of the intervals, they say that
- they are too abstract and only needed for very abstract code
- the readability of the code with them only worsens
- intervals slow down code
Let's see completely worker-peasant practical task, in order to understand whether this criticism is valid and is it true that Eric Nibler was bitten by Bartosz Milewski and writes range-v3 only with the full moon .
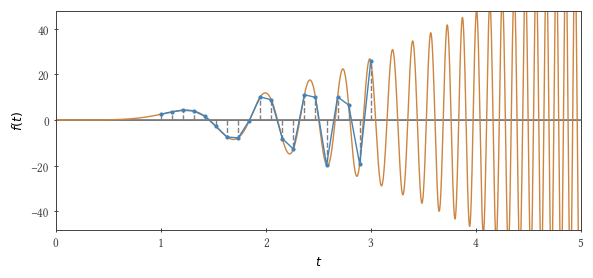
We will integrate the following function using the trapezoid method: $ inline $ f (t) = 3 t ^ 2 \ sin t ^ 3 $ inline $ ranging from zero to $ inline $ \ tau $ inline $ . If a $ inline $ \ tau ^ 3 / \ pi $ inline $ equals an odd number, then the integral is 2.
So, the problem: we write a prototype of a function that calculates the integral by the trapezoid method . It seems, at first glance, that abstractions are not needed here, but speed is important. Actually this is not true. For work, I often have to write “number crushers”, the main user of which is myself. So I also have to support and deal with their bugs (unfortunately my colleagues - not always just me). And it also happens that some code is not used, say, a year, and then ... In general, documentation and tests also need to be written.
What arguments should an integrator function have? Integrable function and grid (set of points $ inline $ t_1, t_2, t_3 ... $ inline $ used to calculate the integral). And if everything is clear with the integrated function ( std::function
will be just right here), then in what form should the grid be transmitted? Let's get a look.
Options
To begin with - to have something to compare performance with - we will write a simple for
loop with a constant time step:
// trapezoidal rule of integration with fixed time step; // dt_fixed is the timestep; n_fixed is the number of steps double integrate() { double acc = 0; for(long long i = 1; i < n_fixed - 1; ++i) { double t = dt_fixed * static_cast<double>(i); acc += dt_fixed * f(t); } acc += 0.5 * dt_fixed * f(0); acc += 0.5 * dt_fixed * f(tau); return acc; }
When using this cycle, you can pass as the arguments to the function the beginning and end of the integration interval, as well as the number of points for this integration itself. Stop - the trapezoid method also happens with a variable step, and our integrable function simply asks to use a variable step! So be it, let us have one more parameter ( $ inline $ b $ inline $ ) to control the "nonlinearity" and let our steps be, for example, as follows: $ inline $ \ Delta t (t) = \ Delta t_0 + bt $ inline $ . This approach (introduce one additional numerical parameter) is probably used in a million places, although, it would seem, its flaw should be obvious to everyone. And if we have a different function? And if we need a small step somewhere in the middle of our numerical interval? But what if an integrable function has a couple of features? In general, we must be able to convey any grid. (Nevertheless, in the examples, until the very end, we will “forget” about the real trapezoidal method and for simplicity we will consider its version with a constant step, keeping in mind that the grid can be arbitrary).
Since the grid can be any, let’s pass its values $ inline $ t_1, t_2, ... $ inline $ wrapped in std::vector
.
// trapezoidal rule of integration with fixed time step double integrate(vector<double> t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; }
There are more than enough communities in this approach, but what about performance? With memory consumption? If before we had everything summed up on the processor, now we have to first fill up a piece of memory, and then read from it. And communication with memory is a rather slow thing. And the memory is still not rubber ( and silicone )
Let's look at the root of the problem. What does a person need to be happy? More precisely, what does our cycle (range-based for loop) need? Any container with begin()
and end()
iterators, and ++
, *
and !=
Operators for iterators. So we will write.
// , , template <typename T> double integrate(T t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; } // ... // class lazy_container { public: long long int n_nodes; lazy_container() { n_nodes = n_fixed; } ~lazy_container() {} class iterator { public: long long int i; // index of the current node iterator() { i = 0; } ~iterator() {} iterator& operator++() { i+= 1; return *this; } // ! bool operator!=(const iterator& rhs) const { return i != rhs.i; } double operator* () const { return dt_fixed * static_cast<double>(i); } }; iterator begin() { return iterator(); } iterator end() { iterator it; it.i = n_nodes; return it; } }; // ... // lazy_container t_nodes; double res = integrate(t_nodes);
We are calculating a new value here. $ inline $ t_i $ inline $ on demand, just as we did in a simple for
loop. There are no memory accesses, and one can hope that modern compilers will simplify the code very efficiently. At the same time, the code of the integrating function has not changed much, and it can still digest std::vector
.
Where is the flexibility? In fact, we can now write any function in the ++
operator. That is, this approach allows, in fact, to transfer a function instead of a single numerical parameter. The grid generated on the fly can be any, and we also (probably) do not lose performance. However, writing a new lazy_container
each time just to somehow distort the grid in a new way doesn’t want to lazy_container
at all (it's the same 27 lines!). Of course, you can make the function responsible for generating the grid a parameter of our integrating function, and lazy_container
too, that is, excuse me, encapsulate it.
You ask - then something will be wrong again? Yes! Firstly, it will be necessary to separately transmit the number of points for integration, which can cause an error. Secondly, the created non-standard bicycle will have to be supported and possibly developed by someone. For example, can you immediately imagine how, with this approach, to compose a combinator for functions in the ++
operator?
C ++ for over 30 years. Many at this age already have children, and C ++ does not even have standard lazy containers / iterators. Nightmare! But everything (in the sense of iterators, not children) will change as early as next year - the standard (possibly partially) will include the range-v3 library, which has been developed by Eric Nibler for several years. We will use the works of its fruits. The code says it all for itself:
#include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... auto t_nodes = ranges::v3::iota_view(0, n_fixed) | ranges::v3::views::transform( [](long long i){ return dt_fixed * static_cast<double>(i); } ); double res = integrate(t_nodes);
The integrating function remains the same. That is, only 3 lines to solve our problem! Here iota_view(0, n)
generates a lazy interval (range, an object that encapsulates the generic begin and end; lazy range is view), which, when iterated at each step, calculates the next number in the range [0, n). It's funny that the name ι (the Greek letter iota) refers 50 years ago to the APL language. Stick |
allows you to write pipelines of interval modifiers, and transform
, in fact, is such a modifier that, using a simple lambda function, turns a sequence of integers into a series $ inline $ t_1, t_2, ... $ inline $ . Everything is simple, as in a fairy tale Haskell.
But how to make a variable step? Everything is just as simple:
As a fixed step, we took a tenth of the period of our function near the upper limit of integration $ inline $ \ Delta t_ {fixed} = 0.1 \ times 2 \ pi / 3 \ tau ^ 2 $ inline $ . Now the step will be variable: you will notice that if you take $ inline $ t_i = \ tau (i / n) ^ {1/3} $ inline $ , (where $ inline $ n $ inline $ Is the total number of points), then the step will be $ inline $ \ Delta t (t) \ approx dt_i / di = \ tau ^ 3 / (3 nt ^ 2) $ inline $ , which is a tenth of the period of an integrable function for a given $ inline $ t $ inline $ , if a $ inline $ n = \ tau ^ 3 / (0.1 \ times 2 \ pi) $ inline $ . It remains to “hem” this to some reasonable partition for small values $ inline $ i $ inline $ .
#include <range/v3/view/drop.hpp> #include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... // trapezoidal rule of integration; step size is not fixed template <typename T> double integrate(T t_nodes) { double acc = 0; double t_prev = *(t_nodes.begin()); double f_prev = f(t_prev); for (auto t: t_nodes | ranges::v3::views::drop(1)) { double f_curr = f(t); acc += 0.5 * (t - t_prev) * (f_curr + f_prev); t_prev = t; f_prev = f_curr; } return acc; } //... auto step_f = [](long long i) { if (static_cast<double>(i) <= 1 / a) { return pow(2 * M_PI, 1/3.0) * a * static_cast<double>(i); } else { return tau * pow(static_cast<double>(i) / static_cast<double>(n), 1/3.0); } }; auto t_nodes = ranges::v3::iota_view(0, n) | ranges::v3::views::transform(step_f); double res = integrate(t_nodes);
An attentive reader noted that in our example, the variable step allowed us to reduce the number of grid points by a factor of three, while there are additional noticeable expenses for computing $ inline $ t_i $ inline $ . But if we take another $ inline $ f (t) $ inline $ , the number of points can change much more ... (but here the author is already becoming lazy).
So timings
We have the following options:
- v1 - simple loop
- v2 - $ inline $ t_i $ inline $ lie in
std::vector
- v3 - makeshift
lazy_container
with makeshift iterator - v4 - intervals from C ++ 20 (ranges)
- v5 - ranges again, but only here the trapezoid method is written using a variable pitch
Here's what it turns out (in seconds) for $ inline $ \ tau = (10 \, 000 \, 001 \ times \ pi) ^ {1/3} $ inline $ , for g ++ 8.3.0 and clang ++ 8.0.0 on the Intel® Xeon® CPU® X5550 (the number of steps is about $ inline $ 1.5 \ times 10 ^ 8 $ inline $ , except for v5, where the steps are three times less (the result of calculations by all methods differs from the two by no more than 0.07):
| v1 | v2 | v3 | v4 | v5 | |
| g ++ | 4.7 | 6.7 | 4.6 | 3.7 | 4.3 |
| clang ++ | 5.0 | 7.2 | 4.6 | 4.8 | 4.1 |
g ++ -O3 -ffast-math -std = c ++ 2a -Wall -Wpedantic -I range-v3 / include
clang ++ -Ofast -std = c ++ 2a -Wall -Wpedantic -I range-v3 / include
In general, the fly went across the field, the fly found a coin!
It may be important to someone
| v1 | v2 | v3 | v4 | v5 | |
| g ++ | 5.9 | 17.8 | 7.2 | 33.6 | 14.3 |
Total
Even in a very simple task, ranges turned out to be very useful: instead of code with self-made iterators on 20+ lines, we wrote 3 lines, while having no problems with the readability of the code or its performance.
Of course, if we needed (for) the ultimate performance in these tests, we would have to get the most out of the processor and from memory by writing parallel code (or writing a version for OpenCL) ... Also, I have no idea what will happen if I write very long modifier chains. Is it easy to debug and read compiler messages when using ranges in complex projects. Will compile time increase. I hope someone ever writes an article about this.
When I wrote these tests, I myself did not know what would happen. Now I know - ranges definitely deserve to be tested in a real project, in the conditions in which you intend to use them.
I went to the bazaar to buy a samovar.
useful links
Documentation and Case Studies v3
code from this article on github
lists in haskell, for comparison
Acknowledgments
Thanks fadey for helping writing this all!
PS
I hope someone comments on such oddities: i) If you take a 10-fold shorter integration interval, then on my Xeon example v2 is 10% faster than v1, and v4 is three times faster than v1. ii) The Intel compiler (icc 2019) sometimes in these examples makes code that is twice as fast as compiled g ++. Is vectorization to blame? Can g ++ be forced to do the same?