
In this article, we will give a definition, list the rules for placing elements in a red-black tree, consider a balancing algorithm, and consolidate what was said on an example. We study this topic in more detail, as well as other types of binary search trees in the course “Algorithms for Developers” .

The red-black tree is a self-balancing binary search tree that guarantees a logarithmic increase in the height of the tree from the number of nodes and the quick execution of the basic operations of the search tree: adding, deleting and searching for a node.
The red-black tree is not completely balanced, in some places its height can vary almost twice. Such an assumption does not asymptotically affect the speed of searching for elements, but significantly speeds up the placement of new elements, because you do not need to “shake” the tree every time you add elements, sometimes it’s enough to just add a red element without touching the others and without changing the “black height” .
Rules for placing elements in a red-black tree
- Each node is either red or black; NIL leaves are always black.
- The root of the tree is always black
- Both descendants of each red node are black
- The path down from any node to any descendant leaf contains the same number of black nodes.
When you insert a new element, it is assigned a red color. To fulfill the first two rules, simply repaint the new vertices in the desired color.
Consider the balancing rules for the implementation of 3 and 4 points.
In each figure, it is assumed that we have already added an element X that violates the 3 rule, we need to change the structure of the tree so that the 3 rule is executed, and 4 is not violated.
Legend of the vertices:
- X - an added element that violates 3 points of the rules.
- P - dad item X
- G - the grandfather of the element X, the father of the element P
- U is the uncle of the element X, the brother of the element P, the second son of the element G.
Case One - Red Uncle
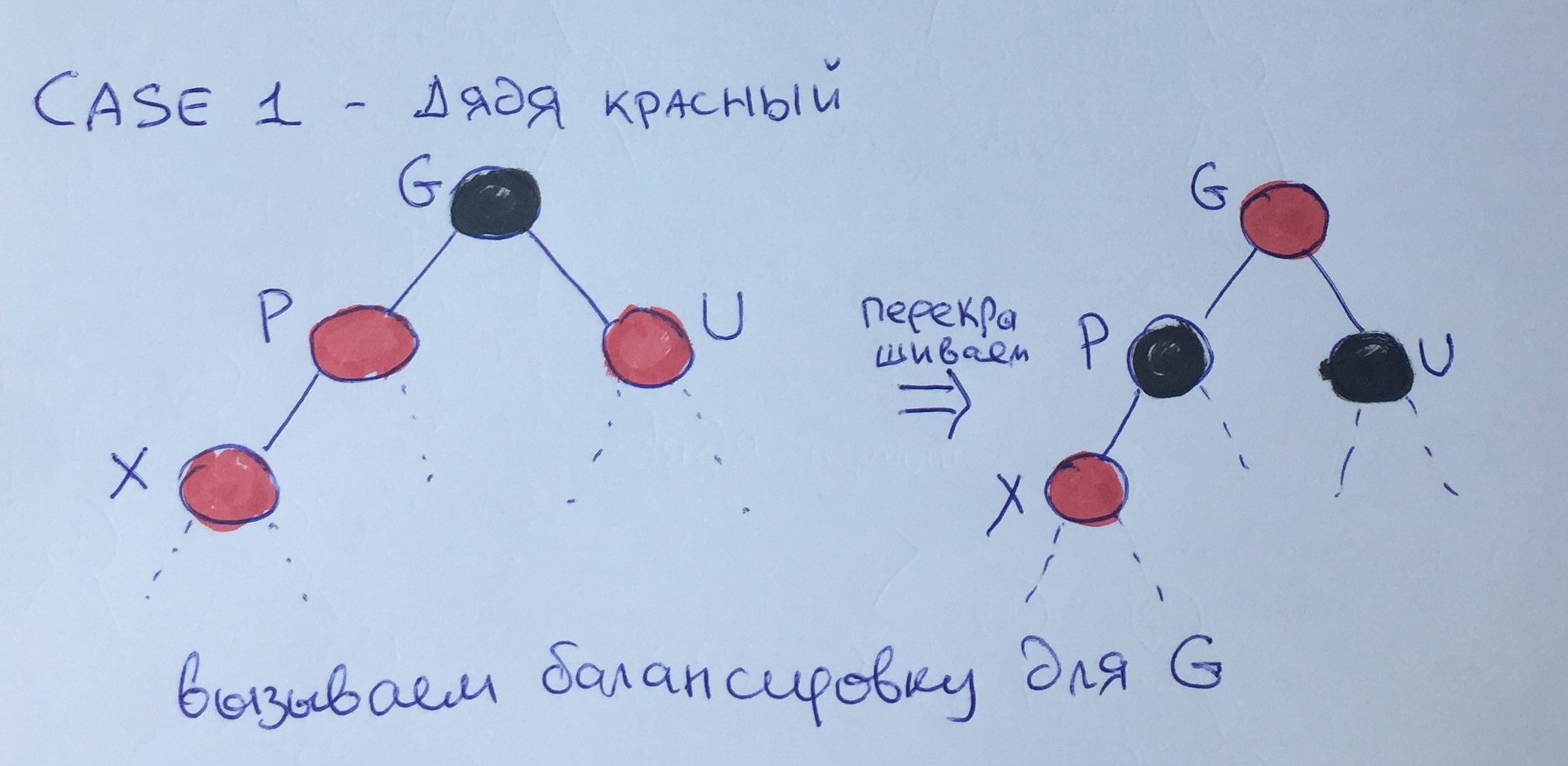
If both the father and uncle are red, then we can “lower” the black color from the level of the grandfather to the level of the father and repaint the nodes, as shown in the figure. In this case, the "black height" will remain the same, however, violation of rule 3 for element G is possible, therefore, it is necessary to recursively call further balancing for this node.
Case two - a black uncle - dad and grandfather in different directions.
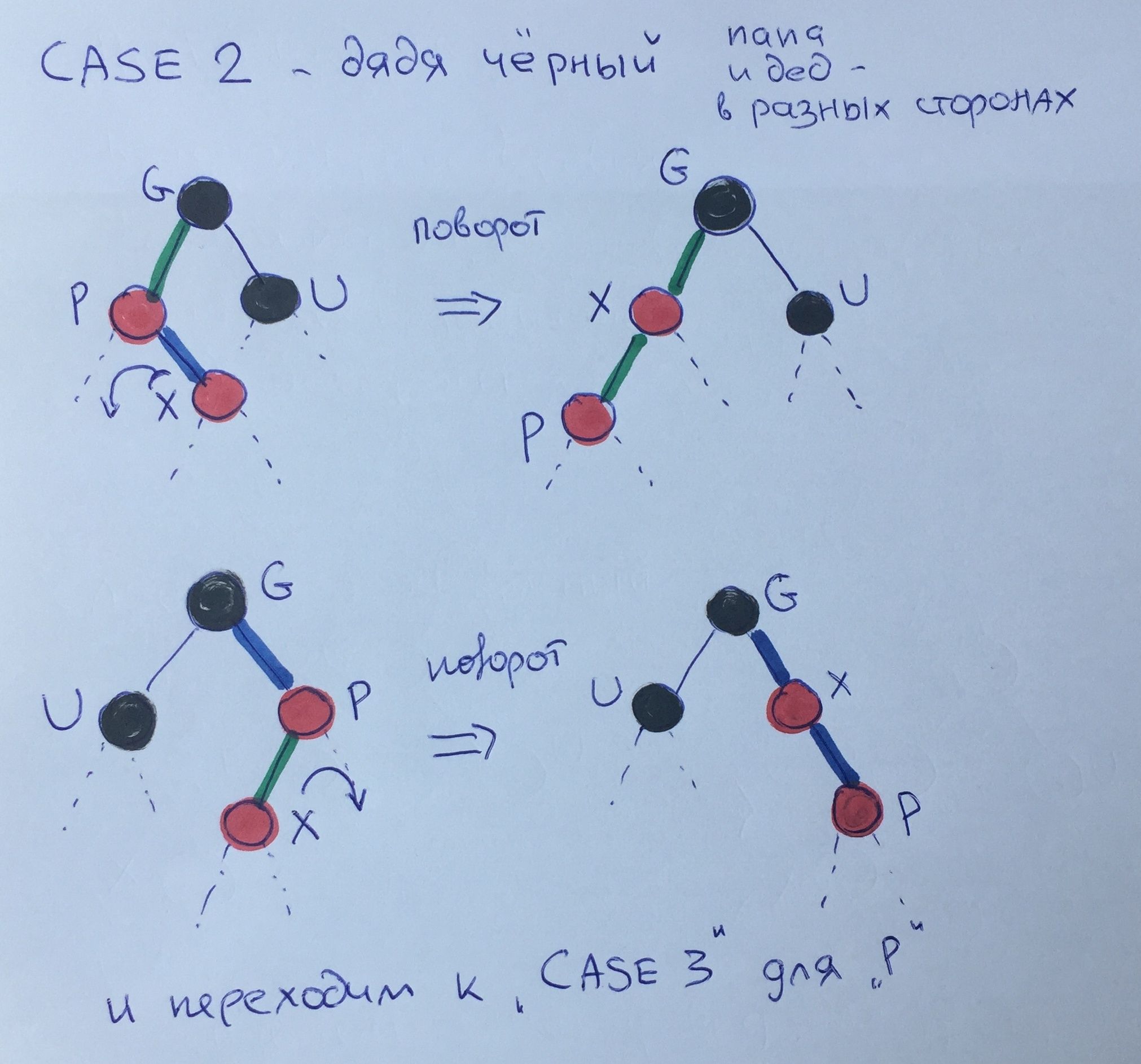
This structure must be brought to the third case, when dad and grandfather go in the same direction. To do this, you need to make a small turn from son X to his father (the rules of turns are not considered in this article) and call 3 cases for element R.
Case Three - Black Uncle - Dad and Grandfather on the Same Side
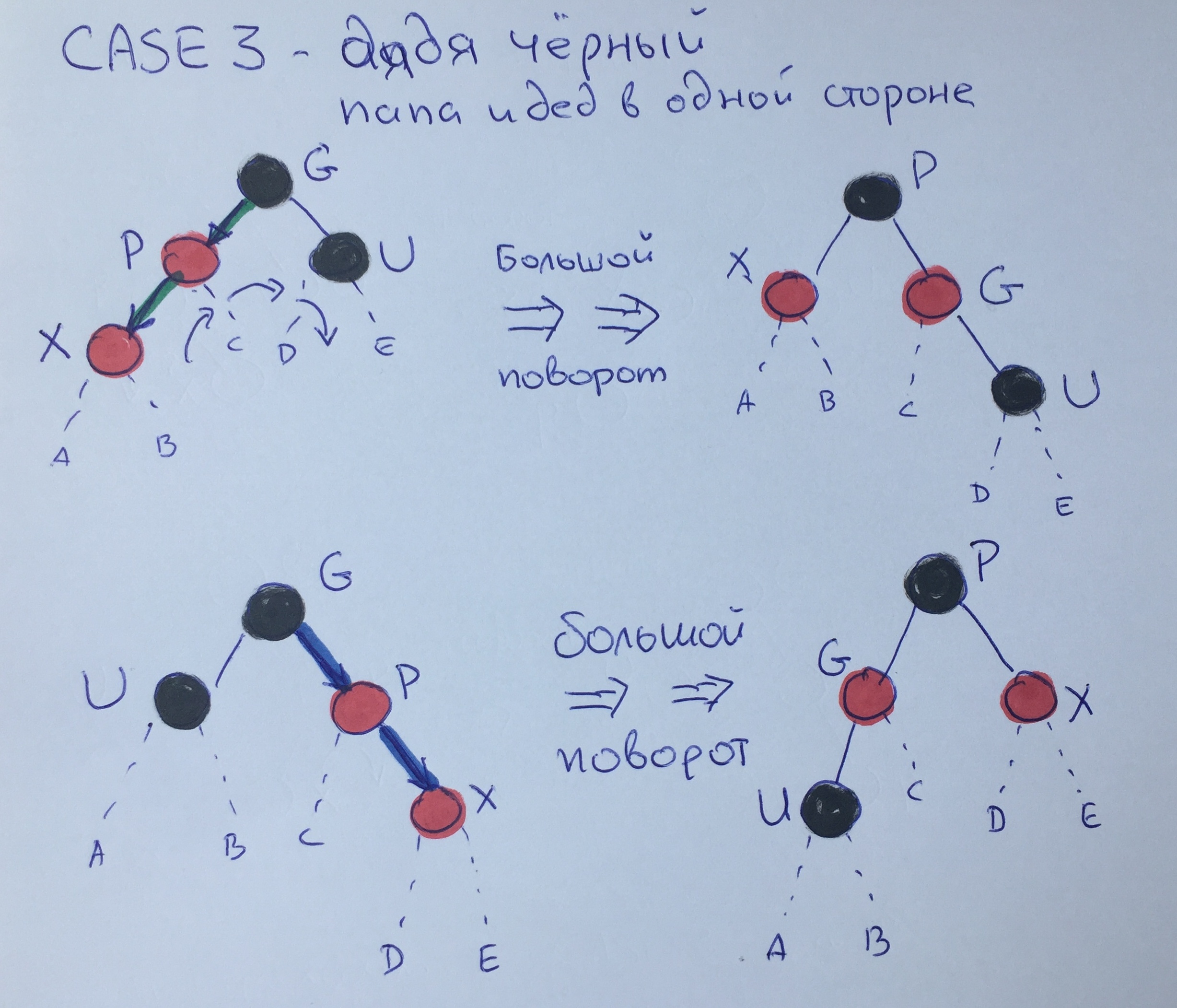
In this case, we can already make a big turn from father through grandfather to black uncle and repaint P in black and G in red. As a result of this rotation, the 3-rule will be satisfied.
Make sure that the 4th rule is also satisfied. Suppose that before the big turn, the black height of the element G was N + 2. Then the height of the "suspended" elements will be as follows:
A = N + 1,
B = N + 1,
C = N + 1,
D = N
E = N.
See for yourself that after rotation, the 4-rule is true for all elements.
Specific example
Now we will consider the process of forming a red-black tree with the sequential insertion of elements 1, 2, 3, 4, 5, and 6.
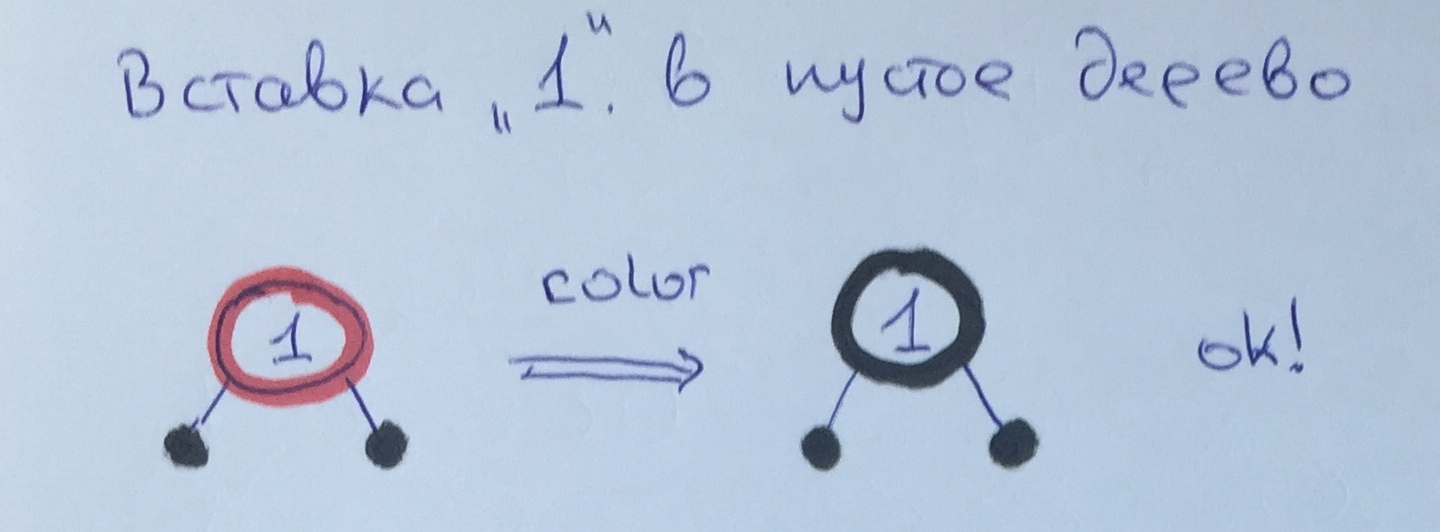
Since element 1 is the root, we simply repaint it to fulfill rule 1.
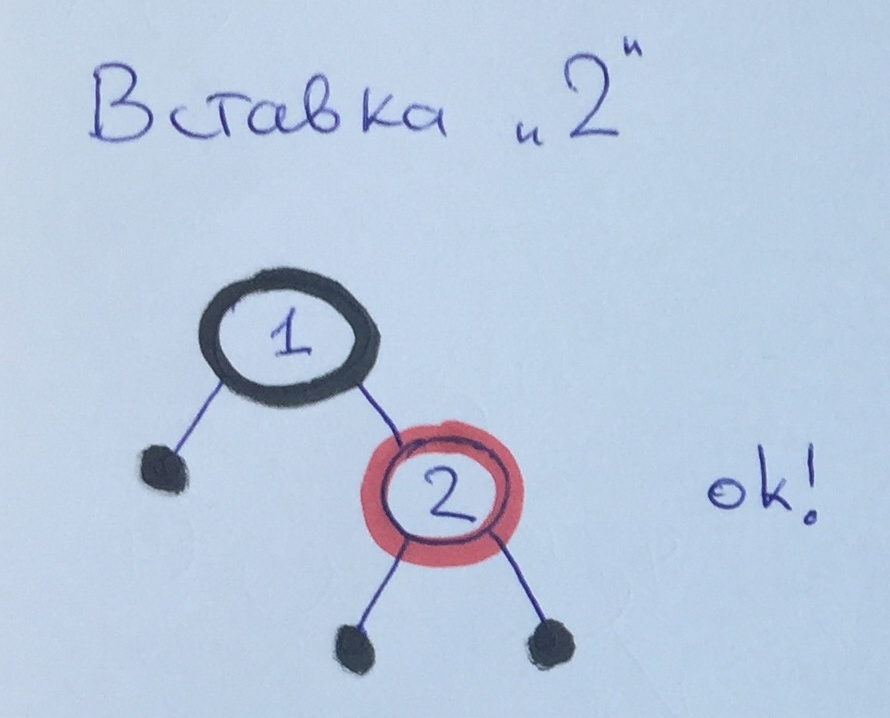
After adding element 2, all the rules are executed.
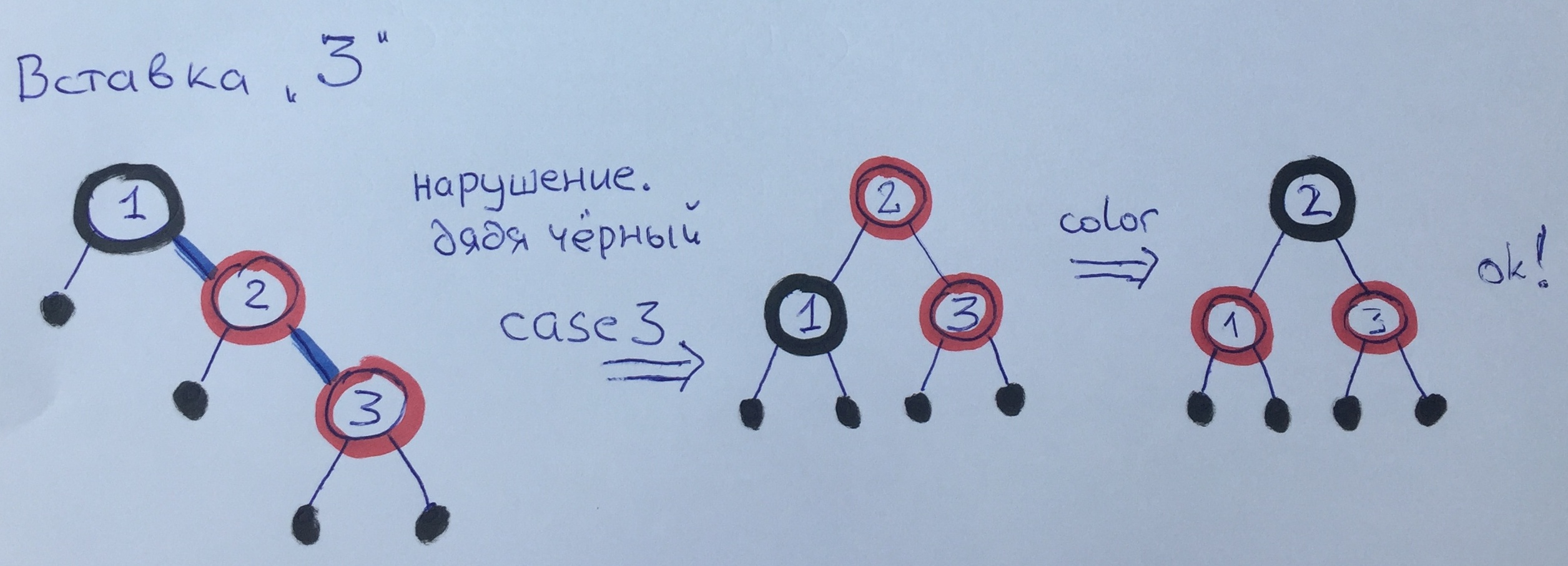
When adding element 3, we violated rule 3. Since we have a black uncle, and grandfather and father on the one hand, we use the third case - we make a turn and repaint.
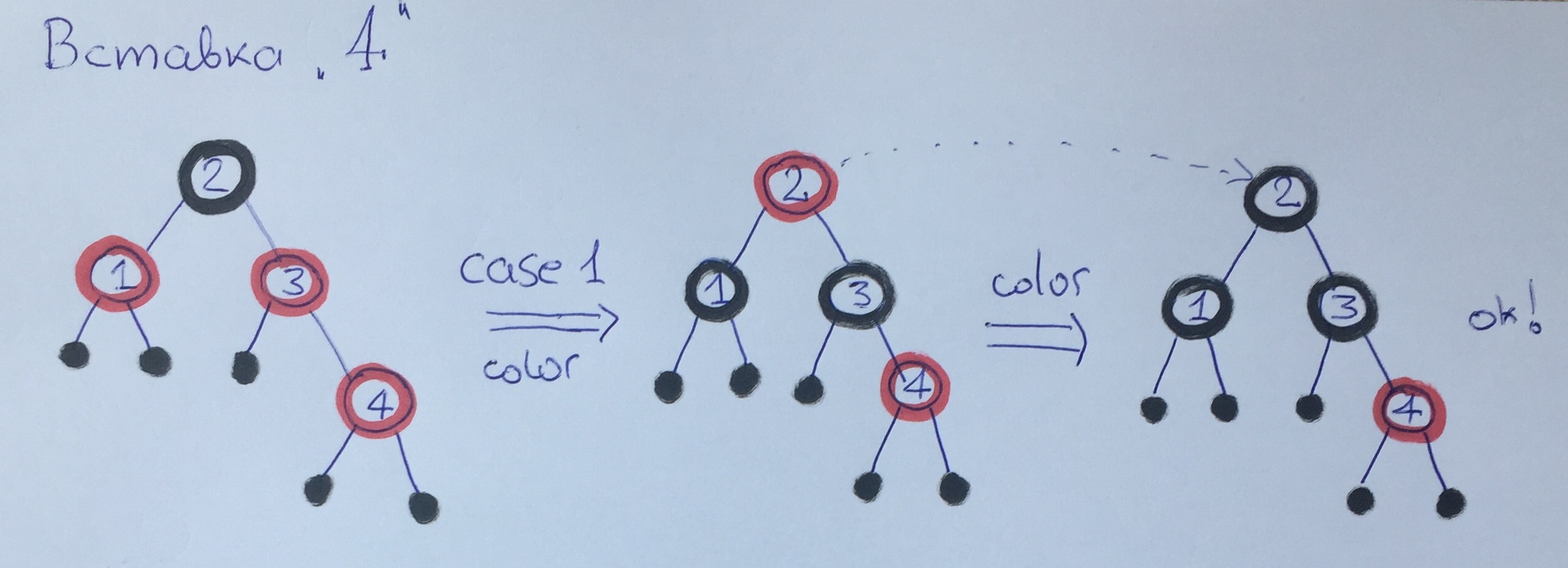
When adding element 4, we again violate rule 3. This time our uncle is red, so we apply the first case with repainting - the black height of the tree will increase by 1. Please note. that the balancing algorithm is launched additionally for the grandfather - element 2, which, like the root, is simply repainted in black.
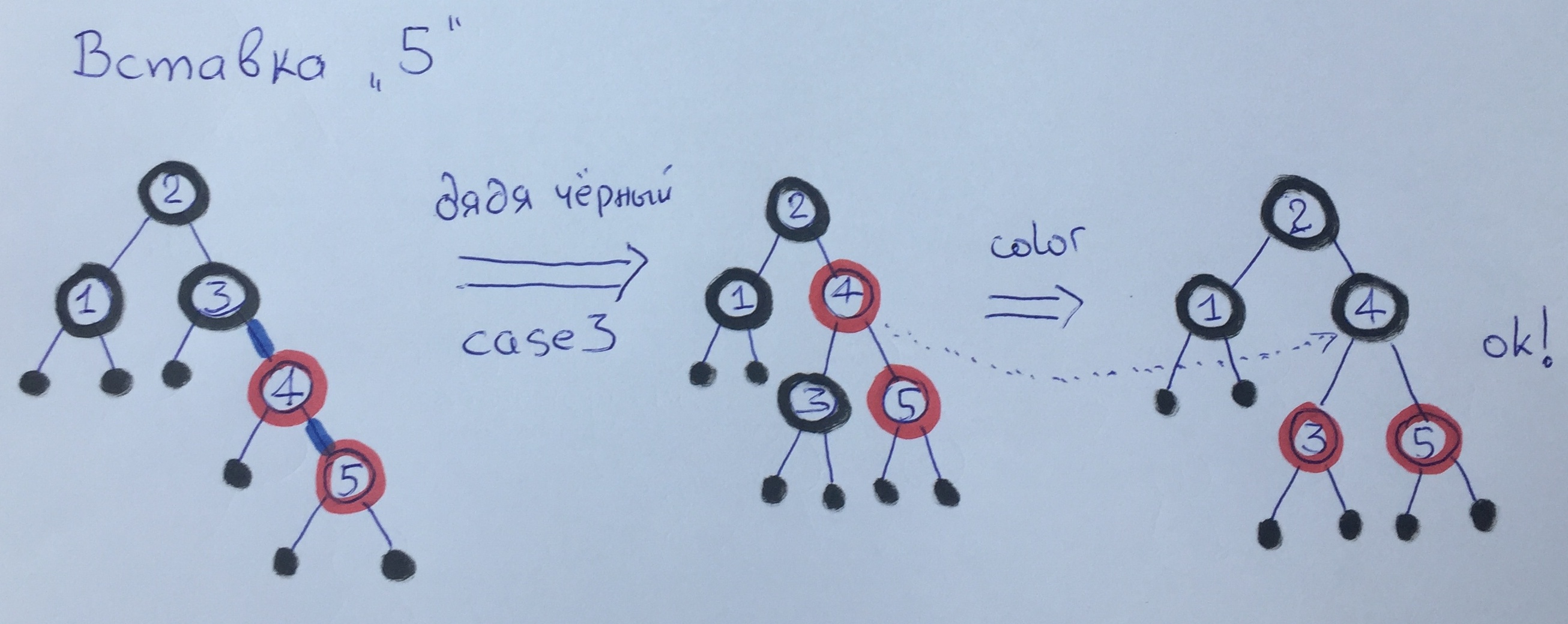
When inserting element 5, we again apply the 3 case - we make a big turn and repaint the vertices. Note that the black height has not changed.
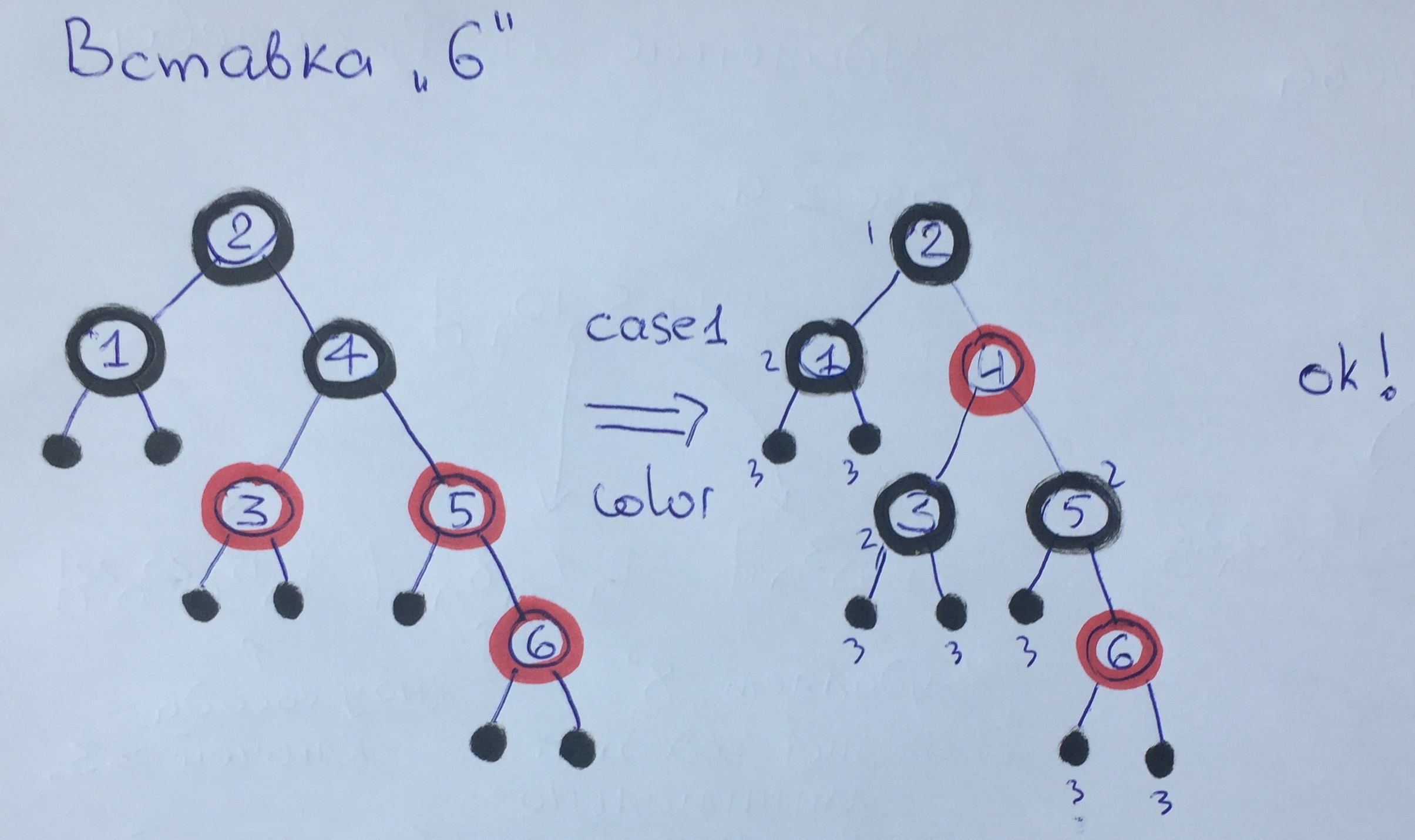
When adding element 6, we again violated rule 3. Since our uncle is red, we apply the first case with repainting, the black height has not changed. The balancing call for 4 elements did not change anything in the tree, since this element does not violate the rules.
So, we got acquainted with the issues of balancing red-black tree, in more detail and with examples of algorithms this topic, as well as varieties of other binary search trees, we consider in the course "Algorithms for Developers" .