Formula for calculating prime numbers and optimizing enumeration of divisors

Greetings! I decided at my leisure to research the problem of finding prime numbers. The topic is extensive and interesting. I want to share a couple of thoughts on it that came to mind. A search on the Internet did not reveal such, pointing to their originality.



Firstly, I have never found a mathematical formula for calculating primes in order. But after all, if there are algorithms, then it is certainly possible to compose formulas using logical functions or operators. I give below the most concise formula that turned out.



For some sequence of numbers $$$(x_ {m}) = {x_ {1}, x_ {2}, x_ {3}, ... x_ {max}}$ we introduce the operator of detection of the first number equal to a:

$$

$$\ mathbf {Dt_ {a} ^ {m}} (x_ {m}): = \ left \ {\ begin {matrix} m \ \ mathbf {if} \ \ forall \, k \ in [1, m) \ x_ {k} \ neq a \ \ mathbf {and} \ \ exists \, k \ in [m, max] \ x_ {k} = a \\ 0 \ \ mathbf {otherwise} \ \ \ \ \ \ \ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ \ \ \ \ \ \ \ \ \ end {matrix} \ right.$$

All primes, starting with 5, can be calculated by the formula:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} ((P_ {n-1} + 2i) \, mod \, P_ {j + 1})), \ \ \ \ forall \, n \ geqslant 3 \\ \ forall \, i_ {max} \ geqslant \ max \ frac {P _ {\ alpha} -P_ { \ alpha -1}} {2} +10 \ ,, \ \ \ alpha \ in [2, n-1]; \ \ j_ {max} = \ pi (\ sqrt {P_ {n-1} + 2i}) - 1$$

Operator $$$\ mathbf {Dt_ {0} ^ {j}}$ iterates over the remainder of dividing each candidate number by simplicity with $$$i$ number $$$(P_ {n-1} + 2i)$ to already found primes up to $$$P_ {j_ {max} +1}$ . Candidate numbers are selected in order from the set of odd numbers larger than the previous prime number $$$P_ {n-1}$ . $$$\ pi (\ sqrt {P_ {n-1} + 2i})$ Is a pi function showing the number of primes $$$\ leqslant \ sqrt {P_ {n-1} + 2i}$ .

Operator $$$\ mathbf {Dt_ {0} ^ {i}}$ iterates over the output values ​​of the operator $$$\ mathbf {Dt_ {0} ^ {j}}$ until it finds 0. Since the series of primes is infinite, this will happen sooner or later. At the exit of the operator $$$\ mathbf {Dt_ {0} ^ {i}}$ so there will always be some number i . Bottom line $$$i_ {max}$ is determined by the maximum difference of adjacent primes smaller than the desired one. The increase in this difference occurs logarithmically. The graph below shows the dependence of the maximum and average growth $$$\ Delta P _ {\ alpha}$ from n for the first 100,000 primes. The maximum value was sampled and averaged for each thousand numbers.

The maximum increase in the difference of primes $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ to previous maximum value $$$max (\ Delta P _ {\ alpha})$ equals 20 (for primes 3312 and 3384). It is in the region where the derivative of the envelope logarithm $$$\ Delta P _ {\ alpha}$ still large enough, and prime numbers are no longer too small. Based on this value, the condition for $$$i_ {max}$ . Schedule $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ for the first 50,000 primes given below. Values ​​were calculated for every thousand.

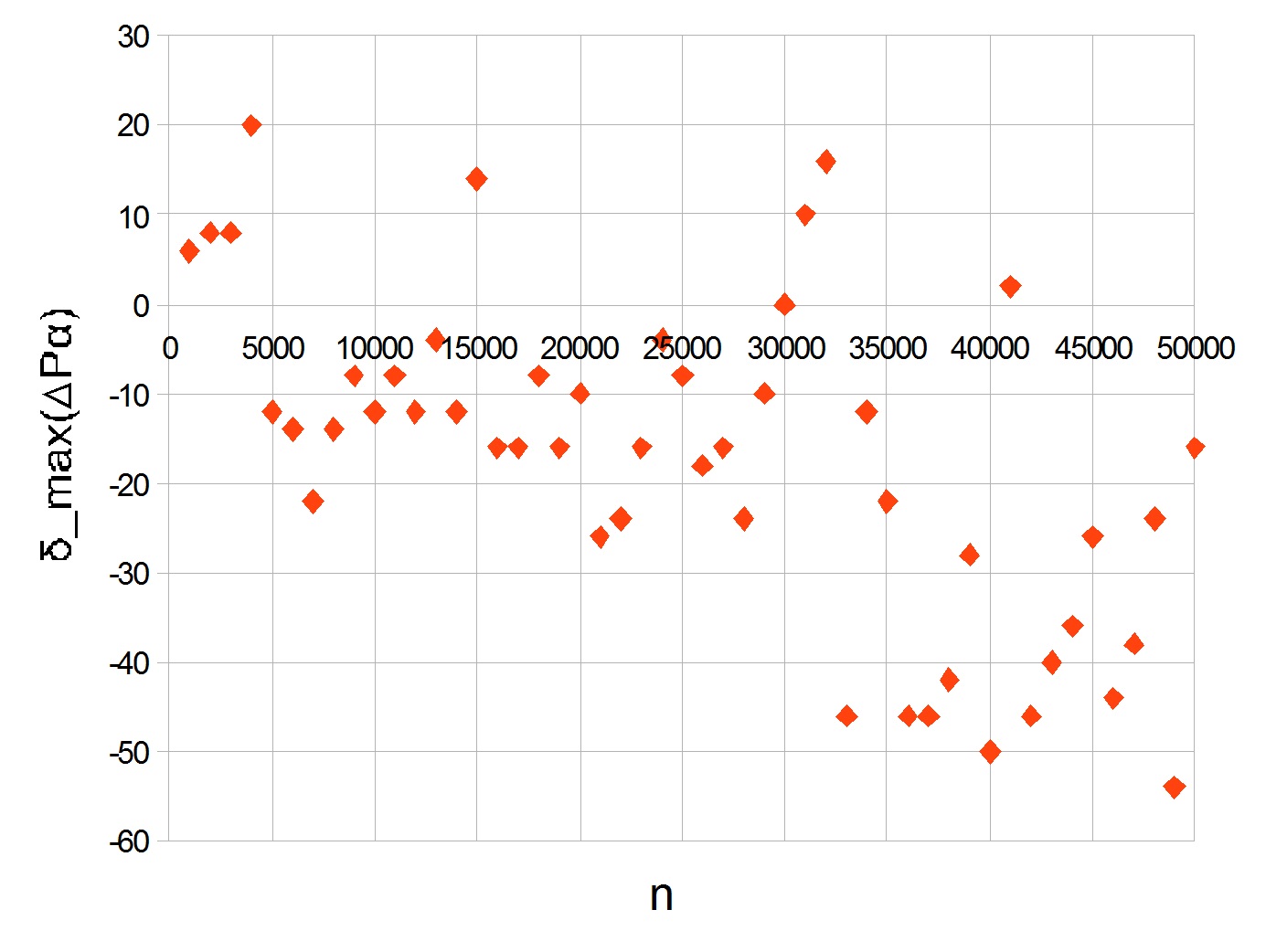
A peak is seen at 20. With increasing n, the graph goes to minus, showing a decrease in the growth rate of large primes.



The second consideration is to optimize the calculation of a sequence of primes.

The algorithm laid down in the formula above is an improved method for enumerating divisors. Improvements are to exclude even numbers from the consideration and check the divisibility of only primes smaller than sq. the roots of the candidate numbers. The most difficult part of the algorithm is the calculation of the set of remainder mod functions. The complexity can be reduced by optimizing this function. However, there is an even more effective way. Let be $$$(r_ {j + 1} ^ {n-1}) = {r_ {2}, r_ {3}, ... r _ {\ pi (\ sqrt {P_ {n-1}})}}$ Is a sequence of residues from dividing the last found prime number into primes from 3 to the root of it. We will make sequences of the form

$$

$$(r_ {i, j + 1} ^ {n}) = {(r_ {2} + 2i) \, mod \, P_2, (r_ {3} + 2i) \, mod \, P_3, ... \\ (r _ {\ pi (\ sqrt {P_ {n-1}})} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1}})}, (P_ {n -1} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1} + 2i})}}$$

in order starting from $$$i = 1$ . The last term is calculated if $$$\ pi (\ sqrt {P_ {n-1} + 2i}) \ neq \ pi (\ sqrt {P_ {n-1}})$ . When at some step of the calculation the remainder $$$r_ {i, j + 1} ^ {n}$ becomes equal to 0, go to the next sequence. This is done until i is found, at which all residues are nonzero. According to the recurrence formula above, this means finding the next prime number. Sequence $$$(r_ {j + 1} ^ {n})$ it must be saved until the next prime number is found.



In the described algorithm, the operation mod is facilitated: divisible by $$$(r_ {j + 1} + 2i) / P_ {j + 1}$ times more dividers. The only exceptions are the occurrence of new simple divisors. When implementing the algorithm, it is necessary to store in the computer memory an array of primes to the root of the sought-for one, as well as a variable array of residuals. The complexity of the algorithm in the general sense (the amount of work) may be less than that of other known methods. The most complex operations in it are the extraction of the square root, the calculation of residues and multiplication. The root can be extracted to the nearest integer. To obtain residues, you can use an effective algorithm based on the general rule of divisibility. Multiplication is used only by 2 relatively small numbers i . The time complexity of the algorithm can be reduced by distributing the work according to the values ​​of i . The segmented sieve obtained in this way should work faster on multi-threaded computers. However, the work performed will be larger due to the increase in dividends. You can also “screw” wheel factorization onto the algorithm. With the optimal size of the wheels, this can reduce complexity in a certain range of n - until the hardware "wilds" slow it down.



Perhaps someone will come in handy my thoughts.