I believed harmony in algebra ...
My friend’s theory is dry, but the tree of life is always green ...
Who just did not fight about this "problem" .... It was dismantled in ancient Greek tragedies, the great Shakespeare told us the story of Romeo and Juliet, Andrzej Wajda dismantled it from both sides in the Anatomy of Love. But people never got to the bottom of the truth until scientists took up the decision. True, not everything seems quite convincing to psychologists. They themselves sometimes even after their own divorce begin to analyze the history of their departed love. Well, write books that sometimes go like hot cakes. They are written by experts! What can I say? Almost nothing personal - just business ...
And finally, not poets with writers and psychologists took love by the throat. Mathematics is the queen of sciences. Is she able to cope with an eternal problem? Books are published, for example, by John Gotman, “The Mathematics of Marriage,” and other authors. Mathematicians consider the development of romantic relationships as a dynamic process ...
And it all starts, as expected, with definitions. How to identify love qualitatively and quantitatively? Researchers classify the problem by type: love affair, passion, fidelity. Moreover, each species has a complex set of feelings. But in addition to love for another person, there is love for oneself, for life, for humanity ...
At the same time, the opposite of love - in the mathematical model - cannot be hatred, since both of these feelings can coexist at the same time. For example, someone may like some manifestations of a partner, but others may be nasty. Therefore, it is unrealistic to assume that the love of an individual is influenced only by his own feelings, and the feelings of the other partner are independent of other influences, and that the parameters characterizing the interaction of two people remain unchanged and thus exclude the possibility of learning and adaptation.
Complexity even in a minimal restricted model increases dramatically when three or more variables are introduced into the equations of nonlinearity and / or.
* Note: translator. In my opinion, such studies can also revive mathematics itself, attract the attention of the public, usually estranged from this abstract science.
Simple linear model
The love story of Romeo and Juliet in time (t) can be represented using the functions * R (t) - Romeo's love for Juliet and J (t) - Juliet's love for Romeo.
Then a simple linear model of their relationship is expressed by equations (1)

a and b - parameters of the romantic style of Romeo
c and d - Juliet style options
a - characterizes how Romeo is enveloped in his own feelings
b - how much Romeo is embraced by Juliet's feelings
One of the articles (Gotman et al., 2002) uses the term “behavioral inertia” for the first and the “influence function” for the second parameter. Although at a = 0, the inertia becomes greatest. The dynamic model under such conditions is two-dimensional and controllable by the initial conditions and four parameters, which can be positive or negative.
A simple linear model was proposed by Rinaldi, 1998a. At the same time, a free term is added to each derivative in order to take into account the attractiveness (or antipathy with a negative value), which each of the partners shows to the other in the absence of other feelings. Such a model is more realistic because it allows feelings to grow from a state of indifference and provides a balance that is not characterized by complete apathy. All this is described in this way only by entering two additional parameters. While the state of non-apathetic equilibrium can be very important for the individuals in question, this does not change the dynamics otherwise than by moving the state space RJ.
Romantic styles
Romeo can exhibit one of four romantic styles depending on the signs a and b, with the notation given by the author of the work (Strogatz, 1994) and his students:
- Passionate desire: a> 0, b> 0 (Romeo is enveloped in Juliet's own feelings and feelings.)
- Narcissistic type: a> 0, b <0 (Romeo is more enveloped in his own feelings, he is detached from Juliet's feelings.)
- Cautious (or reliable lover): a <0, b> 0 (Romeo moves away from his own feelings, but he is overcome by Juliet's feelings.)
- Hermit: a <0, b <0 (Romeo detaches himself from Juliet's own feelings and feelings.)
Since four styles of behavior are also possible for Juliet, there are 16 possible combinations of pairs, each with its own dynamics, although half of them correspond to a permutation of R and J.
Equations (1) determine a single equilibrium point for R = J = 0, which corresponds to a mutually indifferent relationship, or the so-called “plateau of love” (in the Rinaldi model, 1988), with a description of behavior through eigenvalues (2)
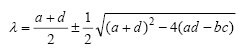

Focus Forking Saddle
Fig. 1. The dynamic situation near the equilibrium point in two-dimensional space, according to equation 1.
Triangle of love
A more mathematically rich model is obtained when a third person is added to a simple model, in particular because alliances may arise in which two individuals can unite against a third. Suppose Romeo has another lover, Genevieve, although the third person in question may be a child or another relative. In this case, the state space becomes more likely six-dimensional than two-dimensional, since each of the three has feelings for the other two, and twelve parameters arise if each can take different styles in relation to the other, even if the natural attraction is ignored, ( reviewed by Rinaldi, 1998a).
In the simplest case, Juliet and Genevieve may not know about each other's existence, and Romeo may show the same romantic style in relation to both. The resulting four-dimensional system is then transformed into two divided two-dimensional systems, until Romeo’s feelings for Juliet are somehow influenced by Genevieve’s feelings for him, and the same is true for Genevieve.
Nonlinear effects
There are an infinite number of ways to input non-linear effects. Imagine that Romeo responds positively to Juliet's love, but with an excessive manifestation of her love, he feels as if strangled and exhibits an adverse reaction. Conversely, if Juliet shows enough dislike, Romeo can try to become pleasant to her.
In this case, it is possible to replace bJ in equation 1 with the logistic function bJ (1 - | J |) corresponding to the measurement of J in units from the condition that J = 1 corresponds to the value at which her love becomes counterproductive. Qualitatively similar results follow from the function bJ (1 - J2), which is the case considered by Rinaldi (1998b) for the 14th-century Italian poet Platonic love model for beautiful Laura, bound by marriage. Assuming the same for Juliet, we get:
(four)

There are 4 equilibrium states, including one at the origin. Figure 3 shows the steady focus at which Juliet. as a “passionate longer” (c = d = 1) leads Romeo's “hermit” (a = b = –2) to a state of mutual love at R = J = 2. A similar model for cautious (reliable) lovers with sigmoidal nonlinearity also leads to stable equilibrium (Rinaldi and Gragnani 1998). Equations 4 obviously do not allow limit cycles, and chaos does not occur as long as the system is two-dimensional.
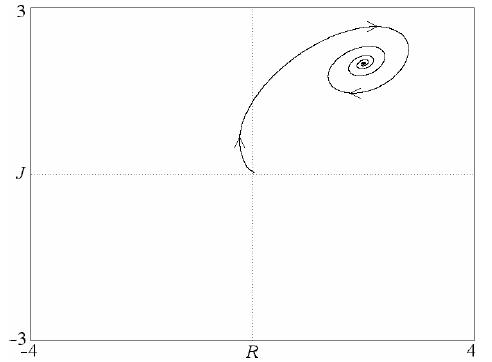
Fig. 3. One of the solutions for the nonlinear model according to equation 4.
Perhaps the application of nonlinear effects to triangles of love.
Afterword
Some of the linear dynamic models of love exhibit surprisingly complex dynamics, while much of them seems to be similar to the known experience in relationships. If there are three or more variables and even the simplest nonlinear effects are introduced, chaos can occur. An interesting extension of the model can be imagined when considering a group of interacting personalities, for example, for cases of a large family or commune. Such models, of course, are very simplified, since love is taken into account as a simple scalar variable, and the reactions of individuals in relation to their own love and the love of other personalities for them are consistent and mechanistic, without taking into account external influence factors.
PS Love will live without mathematics, but mathematics evokes the love of self for people who value true harmony.
Literature:
Julien Clinton Sprott. Dynamical models of love. Nonlinear Dynamics Psychology and Life Sciences • August 2004
Rinaldi, S. (1998a). Love dynamics: the case of linear couples. Applied Mathematics and Computation, 95, 181-192.
Rinaldi, S. & Gragnani, A. (1998). Love dynamics between secure individuals: A modeling approach. Nonlinear Dynamics, Psychology, and Life Sciences, 2, 283-301.
Rinaldi, S. (1998b). Laura and Petrarch: An intriguing case of cyclical love dynamics. SIAM Journal on Applied Mathematics, 58, 1205-1221