Grover Algorithm and Data Search

Hello, habrozhiteli! We recently handed over to Chris Bernhard’s book Quantum Computing for Real IT . Here they decided to share an excerpt from the book "Grover's Algorithm and Data Search"



We are entering the era of big data. Searching gigantic datasets efficiently is currently a burning concern for many large companies. Grover's algorithm is theoretically capable of speeding up data retrieval.



Love Grover invented his algorithm in 1996. Like the algorithms of Deutsch and Simon, it has a higher execution speed compared to classical algorithms in terms of query complexity. However, we will not be able to implement the current data retrieval algorithm without oracles who could ask their questions. We must construct an algorithm that performs the work of the oracle. But before we start talking about the implementation of the Grover algorithm, let's see what it does and how.

Grover Algorithm

Imagine you have four playing cards. They are turned shirts up. You know that one of them is an ace of worms and you need to find it. How many cards will you have to flip until you know where the ace of hearts lies?



If you are lucky, you will find the desired card on the first try, if you are not lucky, you can flip three cards, and not one of them will be an ace of worms. In the worst case, turning over three cards, you will know for sure that the last card is the ace of worm you are looking for. So, we can find out where the ace is by flipping from one to three cards. On average, you need to flip 2.25 cards.



This is one of the tasks that Grover's algorithm solves. Before starting the description of the algorithm, we reformulate the problem. We have four binary sequences: 00, 01, 10 and 11. We have a function f that returns 0 for three of these sequences and 1 for the fourth sequence. We need to find the binary sequence corresponding to the output value 1. For example, we can get the following results: f (00) = 0, f (01) = 0, f (10) = 1 and f (11) = 0. Now the problem is is to find out how many times the function should be calculated to get the result f (10) = 1. Here we simply reformulated the problem by replacing playing cards with functions, so the answer to this question is already known: as before, on average, it will be necessary to calculate the function 2.25 times.



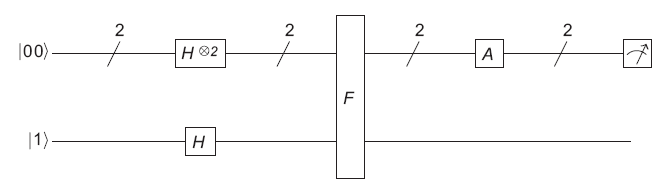
As with all complexity query algorithms, we will construct an oracle - a gate that encapsulates a function. The oracle for our example, where there are only four binary sequences, is shown in Fig. 9.1.



The chain for the Grover algorithm is shown in Fig. 9.2.



The algorithm performs two steps. At the first, the sign of the probability amplitude is turned over, associated with the place we are trying to find. The second reinforces this probability amplitude. Let's see how the chain does this.









After transmission through the Hadamard valves, the two upper qubits get the state









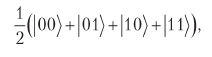
and the lower qubit has a state







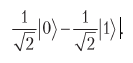
The combined state can be written as









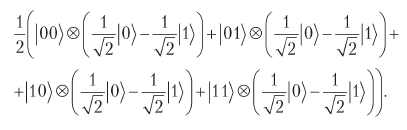
The qubits then pass through gate F. It inverts 0 and 1 in the third qubit to the location we are trying to find. For our case f (10) = 1 we get











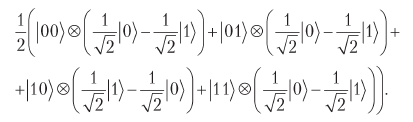
It can be rewritten as











As a result, we get two upper qubits, not confused with the lower, but the amplitude of probability 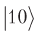will change sign, indicating the desired location.



If we measure the upper two qubits at this step, we get one of four locations, while all four possible answers are equally probable. We need to take another step - to increase the amplitude of probability. Amplification is carried out by reversing the sequence of numbers relative to their average. If the number is above average, it flips and becomes below average. If the number is below average, it flips and becomes above average. In each case, remoteness from the average is maintained. To illustrate, we use four numbers: 1, 1, 1, and –1. Their sum is 2, and the average is 2/4, or 1/2. Then we start sorting through the numbers in the sequence. The first number is 1. It is 1/2 above the average. After the coup, it should be 1/2 lower than average. In this case, it will turn to 0. The number –1 is 3/2 lower than the average. After the coup, it should become 3/2 above the average, that is, turn into 2.



Two upper qubits currently have a state









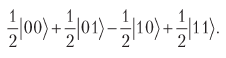
Turning the amplitudes relative to the average, we get .

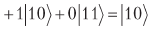Having completed the measurement, we will definitely get 10, that is, a revolution relative to the average gives us exactly what we need. All we have to do is make sure that there is a gate or, equivalently, an orthogonal matrix describing a revolution relative to the average. Such a matrix exists:









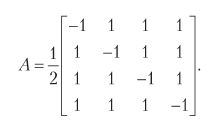
As a result of the action of the valve on the upper two qubits, we get









In this example, where we have only two qubits, we should use the oracle only once. It is enough for us to ask the only question. For the case n = 2, the Grover algorithm gives an exact answer after a single question, whereas in the classical case, on average, 2.25 questions need to be asked.



This idea extends to the case of an arbitrary number of n qubits. We begin by turning the sign of the probability amplitude, which corresponds to the desired location. Then we carry out a revolution relative to the average. However, in this case, the amplification of the amplitude does not occur as significantly as in the situation with two qubits. Take for example eight numbers, seven of which are 1 and one is -1. Their sum is 6, and the average is 6/8. After a flip, the average 1 will turn 1/2, and –1 will turn 10/4. As a result, in the presence of three qubits, measuring one qubit after amplification of the amplitude, we will obtain the desired location with a higher probability than the others. The problem is that there is a significant chance of getting the wrong answer. We need a higher probability of getting the right answer - we need to further amplify the amplitude before measuring. The solution is to transfer all qubits back through the chain. We again flip the sign of the probability amplitude associated with the desired location, and again flip relative to the average.



Consider the generalized case. We need to find something in one of the m possible locations. To find it in the classical way, in the worst case we have to ask m - 1 questions. The number of questions grows in proportion to m. Grover calculated a formula that determines how many times his chain needs to be used to get the maximum probability of a correct answer. The number that this formula gives grows proportionally 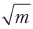. This is quadratic acceleration.

Grover Algorithm Applications

There are several problems with the implementation of the algorithm. First, quadratic acceleration is evaluated relative to the complexity request. To use the oracle, it must be created, and if you do not take this task with due care, the number of steps performed by the oracle will outweigh the number of steps that the algorithm saves, and as a result, the algorithm will become slower rather than faster than the classical one. Another problem is that, by determining acceleration, we assume that the data set is disordered. If the data set has a specific structure, you can often find a classic algorithm that uses this structure and searches for a solution much faster. The last problem is related to acceleration. Quadratic acceleration is nothing more than exponential acceleration, which we observed in other algorithms. Is it possible to achieve more? Let's look at these issues.



Both problems associated with the implementation of the oracle and the presence of the structure in the data set are justified and show that in most cases the Grover algorithm has no practical application for searching the database. But in some situations, having a structure in the data makes it possible to create an oracle that acts with high efficiency. In such situations, the algorithm can overtake classic algorithms. The answer to the question of the possibility of achieving greater success has already been given. It is proved that Grover's algorithm is optimal. There is no quantum algorithm capable of solving a problem with more than quadratic acceleration. Quadratic acceleration, although not as impressive as exponential, still provides some benefits. When working with large data sets, any speedup can be valuable.



Probably, the Grover algorithm will find the main application not for search, as was presented above, but for its variations. In particular, the idea of ​​amplifying the amplitude may come in handy.



We examined just a few algorithms, but the Shore and Grover algorithms are considered the most important. There are many other algorithms based on the ideas inherent in these two.1 Now let us turn our attention from quantum algorithms to other fields of application of quantum computing.