Clever Geek Handbook

RESHI.RU - a robot solves and explains school text problems in mathematics

Introduction



When I explained to my child in the 4th grade how to solve a text problem in mathematics, I suddenly understood two things. Firstly, the decision explanation process can be automated. And secondly, for most school computing problems, a universal method is suitable through a system of equations, which for some reason has not yet been studied in the lower grades of the school. Moreover, the development of this method is quite affordable for the middle school student and will allow him to cope with previously inaccessible tasks. The result of this understanding was the RESHI.RU website with a robot explaining the tasks.



The difference from numerous sites with ready-made homework is that the problem can be solved theoretically by any, and not predetermined. But only theoretically, since in practice the robot understands only those types of tasks for which a software implementation has been made. On the tasks of textbooks for the 4th grade, the robot shows 65% of the correct solutions (and if it cannot or doubts, then honestly warns about it), for the 3rd grade - about 80%.

The problem to be solved should be formulated with error-free text, not have graphic information in the condition (pictures, diagrams) and be computational, that is, the answer should be one or more quantities. The values ​​in the condition of the problem can be either numbers or variables.



The robot tries to compose a system of simple equations for the problem and solve it. For some types of tasks, the robot can solve in a school way, which is offered as an additional one.



Nevertheless, the main goal of RESHI.RU is not to solve specific problems, but to explain by examples the universal method of solving through a system of simple equations.



Task example



Consider an example of a robot solving the following problem from the RESHI.RU website.



Two buses left the village and the city towards each other. One bus drove 100 km to the meeting at a speed of 25 km / h. How many kilometers before the meeting the second bus traveled if its speed is 50 km / h.



The robot realized that this is a task for the movement of two objects and he knows how to solve such. Left

correctly select all quantities, understand their types and correlate with these two objects.

As an explanation, the robot displays a sequence of sections, each of which describes one or another aspect, closer to receiving an answer. Here are screenshots of these sections.



















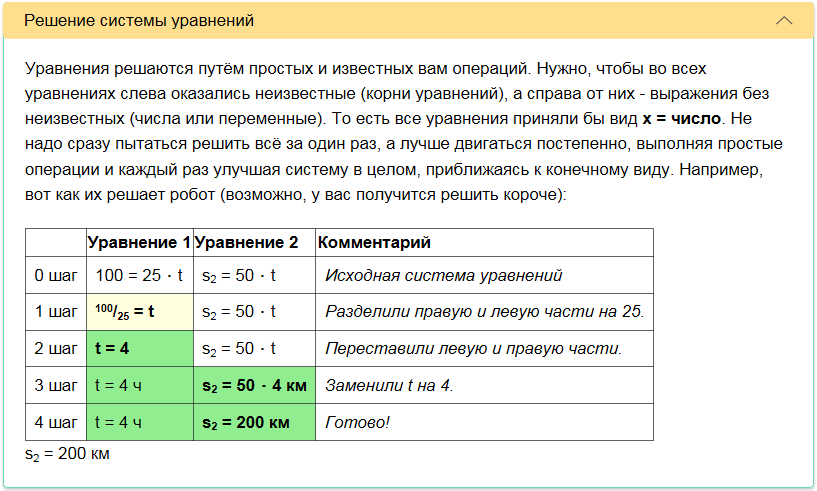
The robot also realized that in addition to the universal method, there is a school method of solution, which is shorter and simpler.







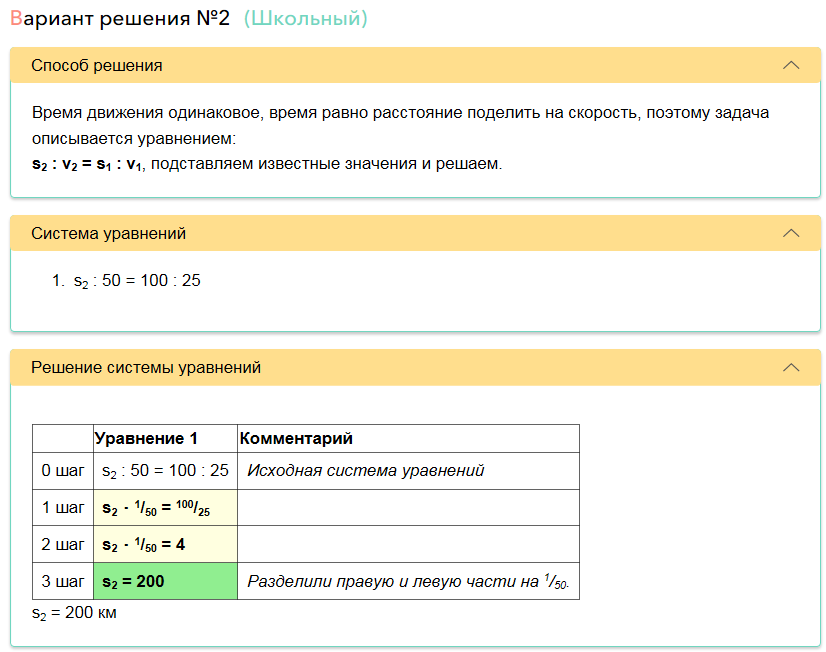
All this together with the scheme is automatically generated for each problem being solved, and not set initially.



The universal way to solve



Most school text problems can be solved by the universal method - through a system of simple equations. If the student learns this method, then he will in principle be able to solve any typical school math problem given by the text.



In the 1st grade, schoolchildren are taught to solve simple problems described by a single equation a = b + c or a = b - c. And in the 3rd grade, after mastering the operations of multiplication with division, simple problems appear on a = b ⋅ s or a = b / c. Compound tasks are those tasks that are not simple, that is, not described by a single equation with three quantities. Here, the student is invited to be smart to either make one complex equation, or reduce the problem to a number of simpler problems that are solved one after another. Compound and subtraction composite tasks are actively offered from the 2nd grade, and from the 3rd grade the complexity increases with the advent of new operations.



But there is another way to solve composite problems, and it consists in compiling a few simple equations (a system of equations), and then solving it in its entirety. Indeed, if a student can solve simple problems (that is, correctly compose a simple equation according to the text of the condition), then for a composite problem he can, in principle, compose his own simple equation for each individual condition. To do this, all occurring quantities must be denoted by their symbols (for example, x, y, z, ...), and the corresponding x = y + z, etc. should be formed for them. Then substitute specific numbers in the equation. And then solve this system by sequentially determining unknown values.



This method may turn out to be more time-consuming for solving a specific task, since some “highlight” usually simplifies the work. But it can not always be found, as it is a kind of art. But the universal method does not require this, being a technology such as "do it once, then do two, and here is the answer."



The robot uses it in a universal way and tries to explain in as much detail as possible on a specific task how it gets a solution. It is assumed that the student will spend some time understanding how the robot does it in order to repeat similar actions in other tasks in the future. However, the robot also offers a school solution if the robot is trained for it for this type of task ( now not for all types, but gradually learns ).



It is useful or not for students - a moot point. On the one hand, this can increase the percentage of tasks solved by students. On the other hand, in some of the students such technological effectiveness can suppress the tender shoots of mathematical savvy. I propose to send to the author or write down my reasonable thoughts and concerns here.



Task classifier



According to a system of simple equations, problems can be automatically classified. This can be useful, for example, in order to offer the student to solve a similar problem to consolidate the skill. Also, the robot can understand what class the task belongs to, because even in the textbooks of the 4th class there are problems of the level of the 1st class!



Currently, the site has downloaded more than 4000 tasks from real textbooks, and you can see this automatic classifier for these tasks.



Robot implementation



Of course, a reasonable question arises - how does this robot do it? I must say that this is a very complex implementation. I have been engaged in natural language text processing for about 10 years, and this is the most difficult task that I have encountered in this area. The difficulty lies in the fact that you need to correctly select numerical values, understand their type and relate to objects. Any inaccuracy in at least one aspect leads to an incorrect result.

I will list only some of the problems that I had to face.





But this is what lies on the surface. At the algorithmic level, these problems are much greater.

The main idea of ​​the algorithm is that specific task handlers that understand their types are implemented. The task is run by all handlers, and which one recognizes its type, that solves the problem. Each handler solves a fairly wide range of tasks of its type.



Now these types are:





When the robot understood the task, that is, attributed it to one of the supported types, having correctly set the values ​​and understanding what needs to be calculated, it can generate its understanding with its own language. By the way, on the site this understanding is displayed to the right of the texts of tasks for textbooks. We give examples from the site.



Condition : The quotient of the numbers 2082 and 6 is equal to the sum of the intended number and the number 48.

Understanding : Find the root of the equation: 2082: 6 = x + 48.



Condition : The play for children began at 11 o’clock and ended at 12 h 35 min. How long did this performance last?

Understanding : There is a time interval. The beginning of the interval is 11 hours. The end of the interval is 12 hours 35 minutes. How long is the interval?



Condition : Anya is 12 years old. She is 3 times older than her brother. How old is Anya older than her brother?

Understanding : There are 2 numerical values: Ani's age and brother's age. Ani's age is 12, he is 3 times more than his brother's age. How much more is Ani's age than her brother's?



Condition : One turner makes 8 parts every hour, and another - 7 parts. How many hours will they produce 90 parts together if their output per hour does not change?

Understanding : There are 2 objects: Turner No. 1 and Turner No. 2. The number of parts in hours of turner No. 1: 8 parts. The number of parts in hours of turner No. 2: 7 parts. The total number of parts together: 90 parts. All objects have the same time. What does time mean in hours?



Condition : Two comrades, Misha and Kolya, came out of two villages at the same time towards each other. Misha walked at a speed of 3 km / h, and Kolya - 5 km / h. At the same time as Misha, a dog ran to Kolya. She ran at a speed of 8 km / h. When she reached Kolya, she turned back to Misha, and ran between the guys until they met. How many kilometers did the dog run if the distance between villages is 16 km?

Understanding : Two objects (Misha and Kolya) simultaneously started moving towards each other from a distance of 16 km. Between them, the 3rd object (dog) moves back and forth at a speed of 8 km / h. The first object (Misha) moved at a speed of 3 km / h. The second object (wheel) moved at a speed of 5 km / h. Which path in km did the 3rd object overcome?



Condition : In the room, the length of which is 8 m, and the width is 2 m less than the length, the floor must be painted. How much paint will you need if you spend 150 g per 1 m2?

Understanding : A rectangle 8 meters long. Width 2 meters less than length. The area is filled with elements of 150 g per unit area. How many elements are there over the entire area?



What's next?



The following development directions are planned:





The implementation of these areas will depend on the actual relevance of the site.


More articles:


All Articles