Arend - HoTT-based dependent type language (part 1)
In this post, we’ll talk about the newly released JetBrains language with Arend dependent types (the language is named after Gating Rent ). This language has been developed by JetBrains Research over the past few years. Although the repositories a year ago were made publicly available on github.com/JetBrains , the full release of Arend only happened in July this year.
We will try to tell how Arend differs from existing systems of formalized mathematics based on dependent types, and what functionality is now available to its users. We assume that the reader of this article is generally familiar with dependent types and has heard at least one of the languages based on dependent types: Agda, Idris, Coq, or Lean. However, we do not expect the reader to possess dependent types at an advanced level.
For simplicity and concreteness, our story about Arend and homotopy types will be accompanied by the implementation on Arend of the simplest list sorting algorithm - even with this example you can feel the difference between Arend and Agda and Coq. There are already a number of articles on Habré devoted to dependent types. Let's say about the implementation of sorting lists using the QuickSort method on Agda there is such an article . We will implement a simpler insertion sorting algorithm. In this case, we will focus on the constructions of the Arend language, and not on the sorting algorithm itself.
So, the main difference between Arend and other languages with dependent types is the logical theory on which it is based. Arend uses as such the recently discovered V. Voevodsky homotopy type theory ( HoTT ). More specifically, Arend is based on a variation of HoTT called "interval theory of types." Recall that Coq is based on the so-called calculus of inductive constructions (Calculus of Inductive Constructions), while Agda and Idris are based on the Martin-Löf intensional theory of types . The fact that Arend is based on HoTT significantly affects its syntactic constructions and the operation of the type checking algorithm (typcheker). We are going to discuss these features in this article.
Let's try to briefly describe the state of the language infrastructure. For Arend, there is a plugin for IntelliJ IDEA that can be installed directly from the repository of IDEA plugins. In principle, installing the plugin is enough to fully work with Arend, you still do not need to download and install anything. In addition to type checking, the Arend plugin provides functionality familiar to IDEA users: there is highlighting and alignment of the code, various refactorings and tips. There is also the option of using the console version of Arend. A more detailed description of the installation process can be found here .
The code examples in this article are based on the Arend standard library, so we recommend downloading its source code from the repository . After downloading, the source directory must be imported as an IDEA project using the Import Project command. Arend has already managed to formalize some sections of the homotopy type theory and ring theory. For example, the standard library contains an implementation of the ring of rational numbers Q along with proofs of all the required ring-theoretic properties.
Detailed language documentation , in which many of the points covered in this article are explained in more detail, is also in the public domain. You can directly ask questions to Arend developers in the telegram channel .
Homotopy type theory (or, in short, HoTT) is a type of intensional type theory that differs from the classical Martin-Löf type theory (MLTT, on which Agda is based) and inductive construction calculus (CIC, on which Coq is based), in that, along with statements and sets contain the so-called types of a higher homotopy level.
In this article, we do not set ourselves the goal of explaining the foundations of HoTT in detail - for a detailed exposition of this theory, it would be necessary to retell the whole book (see this post ). We only note that a theory based on the axiomatics of HoTT is, in a sense, much more elegant and interesting than the classical Martin-Löf type theory. Thus, a number of axioms that previously had to be additionally postulated (for example, functional extensionality) are proved in HoTT as theorems. In addition, in HoTT, one can internally define multidimensional homotopy spheres and even count some of their homotopy groups .
However, these aspects of HoTT are primarily interesting to mathematicians, and the purpose of this article is to explain how the HoTT Arend based compares favorably with Agda / MLTT and Coq / CIC by the example of representing such simple and familiar to any programmer entities as ordered lists. When reading this article, it is enough to treat HoTT as a kind of intensional type theory with a more developed axiomatics, which gives convenience when working with universes and equalities.
Recall that languages with dependent types differ from ordinary functional programming languages in that in addition to the usual data types, such as lists or natural numbers, there are types that depend on the parameter value. The simplest examples of such types are vectors of a given length n or balanced trees of a given depth d. A few further examples of these types are mentioned here.
Recall that the Curry - Howard correspondence allows one to interpret statements of logic as dependent types. The main idea of this correspondence is that an empty type corresponds to a false statement, and populated types correspond to a true statement. Type elements can be thought of as evidence of a corresponding logical statement. For example, any element of the type of integers can be thought of as a proof of the fact that integers exist (that is, the type of integers is populated).
Different natural constructions over types correspond to different logical connectives:
Suppose now that we are given some type A and a family of types B parametrized by an element a of type A. Let us give examples of more complex constructions over dependent types.
At this point, we refer the reader to sources in which the Curry - Howard correspondence is examined in more detail (see, for example, a course of lectures or articles here or here ).
All expressions considered in type theory must have some type. Since expressions denoting types are also considered in the framework of this theory, they also need to be assigned a certain type. The question is, what kind of type should this be?
The first naive decision that comes to mind is to assign to all types a formal type
, called the universe (it is so called because it contains all types in general). If we use this universe, the sum constructions and type products mentioned above will receive the signature
, and more complex constructions of the dependent product and the dependent sum will receive the signature
.
At this point, the question arises, what type should the
universe itself have? A naive attempt to say that the type of the universe
, by definition, is
itself leads to the Girard paradox , so instead of a single universe
consider an infinite hierarchy of universes , i.e. the nested chain of universes
, whose levels are numbered by natural numbers, and the type of the universe
, by definition, is the universe
. For the type constructions mentioned above, more complex signatures also have to be introduced.
Thus, universes in type theory are needed so that any expression has a certain type. In some varieties of type theory, universes are used for another purpose: to distinguish between varieties of types. We have already seen that sets and statements are special cases of types. This shows that it might make sense to introduce into the theory a separate Prop universe for statements and a separate hierarchy of Set i universes for sets. This is exactly the approach used in Calculus of Inductive Constructions - the theory on which the Coq system is based.
Consider Arend's definitions of the simplest inductive data types: Boolean type, natural number type, and polymorphic lists. Arend uses the
keyword to introduce new inductive types.
As you can see from the examples above, after the
keyword, you need to specify the name of the inductive type and a list of its constructors. At the same time, the data type and constructors may have some parameters. Let's say in the example above the
type has one parameter
The
list constructor has no parameters, and the constructor: -: has two parameters (one of which is of type
, and the other is of type
). The
universe consists of types that are sets (the definition of sets will be given in the next section). The
allows you to use infix notation for the constructor: -: and, in addition, tells the Arend parser that the operator: -: is a right-associative operation with priority 5.
In Arend, all keywords begin with a backslash character (“\”), an implementation inspired by LaTeX. Just note that the lexical rules in Arend are very liberal:
and even
- all these literals are examples of valid identifiers in Arend. The final example shows how important it is for the Arend user to remember to put spaces between identifiers and colon characters . Note that in Arend identifiers it is not allowed to use Unicode characters (in particular, you cannot use Cyrillic).
Arend uses the
keyword to define functions. The syntax of this construction is as follows: after the
keyword, you need to specify the name of the function, its parameters and the type of the return value. The final element in defining a function is its body.
If it is possible to explicitly specify the expression in which the given function is to be calculated, then token => is used to indicate the body of the function. Consider, for example, the definition of a type negation function.
The return type of a function does not always have to be specified explicitly. In the example above, Arend would be able to independently infer the type
, and we could omit the expression “:
” after the brackets.
As in most formalized mathematics systems, the user does not have to indicate an explicit predictive level for the
universe, and definitions in which universes are used without explicitly specifying a predictive level are considered to be polymorphic .
Now let's try to define a function that calculates the length of the list. Such a function is easy to determine through pattern matching. Arend uses the
keyword for this. After it, you must specify the variables by which the comparison is performed (if there are more than one such variable, then they should be written with a comma). If the comparison is performed for all explicit parameters, then
along with the variables can be omitted. This is followed by a block of points of comparison, separated from each other by a vertical bar "|". Each item in this block is an expression of the form
.
In the example above, parameter A of the
function is surrounded by curly braces. These brackets in Arend are used to denote implicit arguments, i.e. arguments that the user can omit when calling a function or using a type. Note that in Arend you cannot use infix notation to designate constructors when matching with a pattern, so the prefix notation is used in the sample example.
As in Coq / Agda, in Arend all functions must be guaranteed to be completed (i.e., termination checking is present in Arend). In the definition of the length function, this check is successful, because a recursive call strictly reduces the first explicit argument. If such a reduction did not occur, Arend would issue an error message.
Arend allows circular dependencies and mutually recursive functions for which completion checks are also performed. The algorithm of this check is implemented based on the article by A. Abel. In it you will find a more detailed description of the conditions that mutually recursive functions must satisfy.
We previously wrote that examples of types are sets and statements. In addition, we used the keywords
and
to denote universes in Arend. In this section, we will try to explain in more detail how the statements differ from sets in terms of varieties of the intensional type theory (MLTT, CIC, HoTT), and at the same time explain what the meaning of the keywords
,
and
in Arend consists of.
Recall that in the classical Martin-Löf theory there is no separation of types into sets and statements. In particular, in theory there is only one cumulative universe (which is denoted either by Set in Agda, or Type in Idris, or Sort in Lean). This approach is the simplest, but there are situations in which its shortcomings are manifested. Suppose we are trying to implement the "ordered list" type as a dependent pair consisting of a list and proof of its ordering. It turns out that then, in the framework of the “pure” MLTT, it will not be possible to prove the equality of ordered lists consisting of identical elements, which at the same time differ in terms of proof of ordering. To have such equality would be very natural and desirable, so the impossibility of proving it can be considered as a theoretical flaw in MLTT.
In Agda, this problem is partially solved with the help of so-called annotations of immateriality (see the source , in which the list example is discussed in more detail). These annotations, however, are not a construct from the MLTT theory, nor are they complete constructs on types (it is impossible to mark with a type annotation that is not used in the function argument).
In CIC, based on CIC, there are two different universes nested into each other:
(the universe of statements) and
(the universe of sets), which are immersed in the comprehensive hierarchy of
universes. The main difference between
and
is that there are a number of restrictions on variables whose type belongs to
in Coq. For example, they cannot be used in calculations, and comparison with the sample for them is possible only inside the evidence of other statements. On the other hand, all elements of the type belonging to the
universe are equal in the axiom of inconsequential evidence, see the statement in Coq.Logic.ProofIrrelevance . Using this axiom, we could easily prove the equality of the ordered lists mentioned above.
Finally, consider Arend / HoTT's approach to statements and universes. The main difference is that HoTT dispenses with the axiom of inconsequential evidence. That is, there is no special axiom in HoTT that postulates that all elements of statements are equal. But in HoTT, a type, by definition , is a statement if it can be proved that all its elements are equal to each other. We can define a predicate on types that is true if the type is a statement:
The question arises: what types satisfy this predicate, that is, are statements? It is easy to verify that this is true for empty and singleton types. For types where there are at least two different elements, this will no longer be true.
Of course, we want all the necessary logical connectives to be defined over the statements. In Section 1.1, we already discussed how they could be determined using type-theoretic constructions. There is, however, the following problem: not all of the operations we have entered retain the
property. Constructions of the product of types and the (dependent) functional type preserve this property, while constructions of the sum of types and dependent pairs do not. Thus, we cannot use the disjunction and the quantifier of existence.
This problem can be solved using the new design, which is added to HoTT, the so-called propositional truncation . This design allows you to turn any type into a statement. It can be considered as a formal operation, making equal all terms that inhabit this type. This operation is somewhat similar to annotations of immateriality from Agda, however, unlike them, it is a full-fledged operation on types with signature
.
The last important example of statements is the equality of two elements of some type. It turns out that in the general case the type of equality
does not have to be a statement. The types for which it is one are called sets:
All types that are found in ordinary programming languages satisfy this predicate, that is, equality on them is a statement. For example, this is true for natural numbers, integers, products of sets, sums of sets, functions over sets, lists of sets, and other inductive data types constructed from sets. This means that if we are only interested in such familiar constructions, then we can not think about arbitrary types that do not satisfy this predicate. All types found in Coq are sets .
Types that are not sets become useful if you want to deal with the homotopy type theory. For now, we simply refer the reader to the standard library module containing the definition of an n-dimensional sphere , an example of a type that is not a set.
Arend has special universes
and
, consisting of statements and sets, respectively. If we already know that type A is contained in the
(or
) universe, then a proof of the corresponding
(or
)
in Arend can be obtained using
axiom built into the prelude (we give an example of using this axiom in section 2.3).
We have already noted that not all natural constructs on types retain the
property. For example, inductive data types with two or more constructors never satisfy it. As noted above, we can use the propositional truncation construct that turns any type into a statement.
In the Arend library, the standard implementation of propositional truncation is called
. We could define a type of logical “or” in Arend as truncating the sum of types:
In Arend, there is another, simpler and more convenient way to define a propositionally truncated inductive type. To do this, just add the
keyword before defining the data type. For example, the definition of a logical “or” in the Arend standard library is given as follows.
Further work with propositionally truncated types resembles that of types assigned to the
universe in Coq. For example, pattern matching of a variable whose type is a statement is allowed only in a situation where the type of the expression being defined is itself a statement. Thus, it is always easy to define the function
through comparison with the sample, but the inverse function to it, only if the type A
B is a statement (which is rare enough, for example, when types
and
are both statements and mutually exclusive of each other).
Recall also that the peculiarity of the mechanism of universes in Coq is that if some definition was assigned to the
universe, then in no way will it be possible to use it in the calculation. For this reason, Coq developers themselves do not recommend the use of propositional constructions, but advise to replace them with analogues from the universe of sets, if possible. The mechanism of Arend universes does not have this drawback, that is, in certain situations it is possible to use statements in calculations. We will give an example of such a situation when we discuss the implementation of the list sorting algorithm.
Since our goal is to implement the simplest sorting algorithm, it seems useful before that to familiarize yourself with the implementation of ordered sets available in the Arend standard library.
In Arend, classes are used to encapsulate operations and axioms that define mathematical structures, and also to highlight the relationships between these structures using inheritance. Classes are also namespaces, inside of which it is convenient to place constructions and theories that are appropriate in meaning.
The base class from which all order classes in Arend are inherited is the
class, which does not contain any members other than the designation
for the host set (that is, sets on which
descendant
already introduce various operations). Consider the definition of this class from the Arend standard library.
In the definition above, carrier
declared as a class parameter. One may ask, is there a difference in the above
definition from the following definition, in which media E is defined as a class field?
A slightly unexpected answer is that in Arend there is no difference between the two definitions in the sense that any class parameter (even implicit) in Arend is, in fact, its field. Thus, for both
implementations, one could use the
expression to access the field E.
still a difference between the above variants of the
definition, but it is more subtle, we will examine it in more detail in the next section when we discuss class instances ( class instances).
The operation of sorting a list makes sense only if a linear order is specified on the type of objects in the list, so we first consider the definitions of a strict partially ordered set and a linearly ordered set.
From the point of view of type theory, classes in Arend can be considered analogs of sigma types with a more convenient syntax for projections and constructors.More precisely, any Arend class can be considered as a sigma type, the components of which are all unrealized fields of the class.
If the field type is a statement, then such a field is called a property . Properties differ from fields in that their implementations are never evaluated. For example, in StrictPoset field
and
are properties and the field
, and
- no. Properties give a noticeable increase in productivity, since their implementations (which, in fact, are proofs of these properties) are often large, but it usually makes no sense to calculate them.
To implement the sorting algorithm, it is not enough to have an ordered set; you also need to know that this order is decidable. The fact is that Arend usesconstructive mathematics , which means that not all predicates in it are decidable. In particular, equality of elements is not solvable for any type. For example, this is true for integers, but not for many functions over integers, since it is impossible to algorithmically determine whether two functions are equal or not. We can define a class of sets with decidable equality as follows:
A predicate is
defined over statements in a way that
is true if and only if it is
decidable, that is, when either
or negation is true
.
Finally, consider the class
(from the word decidable) from the module
. The class Dec implements solvable linear orders, and, in particular, contains the axiom we need
, meaning that any two elements of the type
are comparable with respect to order <. Thus,
it can be considered as an analogue of the Comparable interface from Java.
The name of the class
coincides with the name of the data type already introduced above
, however, an apparent designation conflict does not actually occur, since the standard library contains this class in a different namespace. We will use
it to designate the class, and not the data type of the same name.
Axioms of linear order follow from the axioms of trichotomy, so it’s logical to immediately check these axioms inside the class
(in the listing above we omitted this evidence for brevity). The example
shows that in Arend multiple inheritance is allowed (
at the same time it is a descendant of
and
), moreover, even diamond inheritance is allowed.
For rhomboid inheritance, there is the following natural restriction: the same field can be implemented in two different ancestors only if these implementations coincide (or if the field is a property, since the implementation is ignored in this case).
If you select a class
in the module
and ask IDEA to show the class hierarchy (usually this is done by pressing [Ctrl] + [H]), you get a tree similar to the picture below.
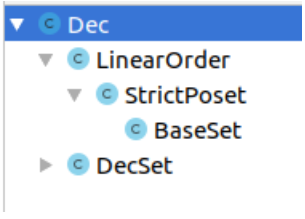
At this point, we suggest that you independently study the full class hierarchy of the Arend standard library (for this, just ask IDEA to show all subtypes
). As you can see, this hierarchy is now very extensive.
Now let's try to create an instance of a strict order class
for the type of natural numbers Nat. In Arend, you can create an instance of a class only for classes that have all the fields implemented. If we follow the analogy between classes and sigma types, then the class whose all fields are implemented corresponds to an empty sigma type (i.e., a singleton type), and creating an instance of the class corresponds to taking the only value of this singleton type.
We begin by defining the order and evidence of its simplest properties: antireflexivity and transitivity. Both of these properties are easily proved by induction by comparison with the sample.
In the examples above, instead of the keyword,
we used
. Lemmas relate to functions in the same way that class properties relate to class fields, that is, expressions for them are never evaluated, and this gives a performance boost. As with class properties, the keyword
can only be used if the type of the result of the function belongs to the universe
.
In the example above
- a clear name for the sample variable, which is a proof of inequality
. We will continue to use similar names for sample variables (i.e. names that match the record without spaces of statements, which these variables are proof of).
Now we can create an instance of the class
. Arend has several different syntax options for this. The first way to instantiate a class is to use a keyword
inside any expression. In this case, an “anonymous class instance” will be created.
An expression
also makes sense without a keyword
: in this case, it denotes an anonymous extension class
. It is not necessary to implement all fields in anonymous extension classes, however, as mentioned above, the operation
cannot be applied to an incompletely implemented class . A view expression
has a type
. Since this type is a descendant of C, it also has type C. Accordingly, in the example above it is true that it
is an instance of the class
.
We have already noted above that class fields are no different from class parameters. In particular, from the point of view of internal representation, expression
is no different from expression
. Note that we could indicate the type of function
as
, and this would not be considered a mistake due to the usual rules of subtyping (a class descendant can be used instead of a parent).
An alternative way to define an instance of a class
is to use a keyword
in the function header (in this case, the type of the function must be specified and be some kind of class).
Finally, let's look at another way to define an instance of a class using the keyword.
Arend implements an algorithm for finding class instances, similar to that in the Haskell language. The implementation of the function
through the keyword is
similar to the implementation through
and differs from it only in that this function will be used during the search for instances of the class
(we will discuss instances just below).
Recall that in the implementation
from the standard library, the carrier set E is defined as a class parameter (and not as a field), and in the last section we said that such an implementation has some difference from the implementation of E as a class field. Now we will comment on this difference in more detail.
We mentioned that class parameters from the point of view of Arend’s internal implementation are no different from class fields. However, Arend has an agreement that the first explicit class argument is not converted by default to a so-called class field, but to a so-called classifier field (this convention works if the " classifier field " is not explicitly selected by the user with a keyword
, a class in Arend may have only one classifier field). Classifying class fields have the following properties:
Let us first explain why instances are needed at all. Suppose that we have implemented through a construction with a keyword
several instances of the class
for various data types, for example, for natural numbers
and integers
(we will call constructed instances
and
).
It is argued that now it is possible to use notation
to indicate order, both in the case where x, y are natural numbers, and in the case where x, y are integers. In the first case, Arend will automatically determine what is meant
, and in the second -
.
We now explain in more detail how the instance search algorithm works. Arend determines that the <field is entered in the class
, in which the field E is declared as the classifying field. Next, Arend calculates the type of arguments of the expression
and tries to find in the current scope the instance of the class
(or its descendant) in which the classifying field E is of the desired type. If such an instance is found, then the implementation of the field
is taken from this instance.
Note that automatic conversion of a class to a type of its classifying field is just a special case of a more general type conversion mechanism in Arend. To allow implicitly casting one type to another, you need to use a special design
inside the associated module of this definition. In Arend, each definition has a so-called associated module.- some namespace used to place various auxiliary constructions in it. To add any other definitions to the associated definition module, the keyword is used
.
Consider the simplest example of using a type conversion mechanism. The function
will be used to implicitly convert natural numbers to integers.
The syntax for the declaration is
similar
with the difference that this function should have only one explicit argument. In this case, either the type of the result or the type of a single argument of the function must coincide with the definition with which the given module is associated (of course, this is possible only for modules associated with the definitions of classes or inductive data types).
Posted by Sergey Sinchuk, Senior Researcher , HoTT Group and Dependent Types at JetBrains Research.
We will try to tell how Arend differs from existing systems of formalized mathematics based on dependent types, and what functionality is now available to its users. We assume that the reader of this article is generally familiar with dependent types and has heard at least one of the languages based on dependent types: Agda, Idris, Coq, or Lean. However, we do not expect the reader to possess dependent types at an advanced level.
For simplicity and concreteness, our story about Arend and homotopy types will be accompanied by the implementation on Arend of the simplest list sorting algorithm - even with this example you can feel the difference between Arend and Agda and Coq. There are already a number of articles on Habré devoted to dependent types. Let's say about the implementation of sorting lists using the QuickSort method on Agda there is such an article . We will implement a simpler insertion sorting algorithm. In this case, we will focus on the constructions of the Arend language, and not on the sorting algorithm itself.
So, the main difference between Arend and other languages with dependent types is the logical theory on which it is based. Arend uses as such the recently discovered V. Voevodsky homotopy type theory ( HoTT ). More specifically, Arend is based on a variation of HoTT called "interval theory of types." Recall that Coq is based on the so-called calculus of inductive constructions (Calculus of Inductive Constructions), while Agda and Idris are based on the Martin-Löf intensional theory of types . The fact that Arend is based on HoTT significantly affects its syntactic constructions and the operation of the type checking algorithm (typcheker). We are going to discuss these features in this article.
Let's try to briefly describe the state of the language infrastructure. For Arend, there is a plugin for IntelliJ IDEA that can be installed directly from the repository of IDEA plugins. In principle, installing the plugin is enough to fully work with Arend, you still do not need to download and install anything. In addition to type checking, the Arend plugin provides functionality familiar to IDEA users: there is highlighting and alignment of the code, various refactorings and tips. There is also the option of using the console version of Arend. A more detailed description of the installation process can be found here .
The code examples in this article are based on the Arend standard library, so we recommend downloading its source code from the repository . After downloading, the source directory must be imported as an IDEA project using the Import Project command. Arend has already managed to formalize some sections of the homotopy type theory and ring theory. For example, the standard library contains an implementation of the ring of rational numbers Q along with proofs of all the required ring-theoretic properties.
Detailed language documentation , in which many of the points covered in this article are explained in more detail, is also in the public domain. You can directly ask questions to Arend developers in the telegram channel .
1. Overview of HoTT / Arend
Homotopy type theory (or, in short, HoTT) is a type of intensional type theory that differs from the classical Martin-Löf type theory (MLTT, on which Agda is based) and inductive construction calculus (CIC, on which Coq is based), in that, along with statements and sets contain the so-called types of a higher homotopy level.
In this article, we do not set ourselves the goal of explaining the foundations of HoTT in detail - for a detailed exposition of this theory, it would be necessary to retell the whole book (see this post ). We only note that a theory based on the axiomatics of HoTT is, in a sense, much more elegant and interesting than the classical Martin-Löf type theory. Thus, a number of axioms that previously had to be additionally postulated (for example, functional extensionality) are proved in HoTT as theorems. In addition, in HoTT, one can internally define multidimensional homotopy spheres and even count some of their homotopy groups .
However, these aspects of HoTT are primarily interesting to mathematicians, and the purpose of this article is to explain how the HoTT Arend based compares favorably with Agda / MLTT and Coq / CIC by the example of representing such simple and familiar to any programmer entities as ordered lists. When reading this article, it is enough to treat HoTT as a kind of intensional type theory with a more developed axiomatics, which gives convenience when working with universes and equalities.
1.1 Dependent types, Curry - Howard correspondence, universes
Recall that languages with dependent types differ from ordinary functional programming languages in that in addition to the usual data types, such as lists or natural numbers, there are types that depend on the parameter value. The simplest examples of such types are vectors of a given length n or balanced trees of a given depth d. A few further examples of these types are mentioned here.
Recall that the Curry - Howard correspondence allows one to interpret statements of logic as dependent types. The main idea of this correspondence is that an empty type corresponds to a false statement, and populated types correspond to a true statement. Type elements can be thought of as evidence of a corresponding logical statement. For example, any element of the type of integers can be thought of as a proof of the fact that integers exist (that is, the type of integers is populated).
Different natural constructions over types correspond to different logical connectives:
- The product of types A × B is sometimes called the type of the pair Pair A B. Since this type is populated if and only if both types A and B are populated, this construction corresponds to the logical “and”.
- The sum of types A + B. In Haskell, this type is called Either A B. Since this type is populated if and only if one of the types A or B is populated, this construction corresponds to a logical “or”.
- Functional type A → B. Any function of this type converts elements of A to elements of B. Thus, such a function exists exactly when the existence of an element of type A implies the existence of an element of type B. Therefore, this construction corresponds to implication.
Suppose now that we are given some type A and a family of types B parametrized by an element a of type A. Let us give examples of more complex constructions over dependent types.
- Dependent function type Π (a: A) (B a). This type coincides with the usual functional type A → B if B is independent of A. A function of type Π (a: A) (B a) converts any element a of type A to an element of type B a. Thus, such a function exists if and only if for any a : A there exists an element B a. Therefore, this construction corresponds to the universal quantifier ∀. For the dependent functional type, Arend uses the syntax
\Pi (x : A) -> B a
, and the term inhabiting this type can be constructed using the lambda expression\lam (a : A) => f a.
- The type of dependent pairs is Σ (a: A) (B a). This type coincides with the usual types of A × B pairs if B is independent of A. The type Σ (a: A) (B a) is populated exactly when there exists an element a: A and an element of type B a. Thus, this type corresponds to the existence quantifier
∃
. The type of dependent pairs in Arend is denoted by\Sigma (a : A) (B a)
, and the terms that inhabit it are constructed using the constructor of the (dependent) pair(a, b)
.
- The equality type is a = a ', where a and a' are two elements of some type A. Such a type is populated if a and a 'are equal, and is empty otherwise. Obviously, this type is an analogue of the equality predicate in logic.
At this point, we refer the reader to sources in which the Curry - Howard correspondence is examined in more detail (see, for example, a course of lectures or articles here or here ).
All expressions considered in type theory must have some type. Since expressions denoting types are also considered in the framework of this theory, they also need to be assigned a certain type. The question is, what kind of type should this be?
The first naive decision that comes to mind is to assign to all types a formal type
\Type
, called the universe (it is so called because it contains all types in general). If we use this universe, the sum constructions and type products mentioned above will receive the signature
\Type → \Type → \Type
, and more complex constructions of the dependent product and the dependent sum will receive the signature
Π (A : \Type) → ((A → \Type) → \Type)
.
At this point, the question arises, what type should the
\Type
universe itself have? A naive attempt to say that the type of the universe
\Type
, by definition, is
\Type
itself leads to the Girard paradox , so instead of a single universe
\Type
consider an infinite hierarchy of universes , i.e. the nested chain of universes
\Type 1 < \Type 2 < …
, whose levels are numbered by natural numbers, and the type of the universe
\Type i
, by definition, is the universe
\Type (i+1)
. For the type constructions mentioned above, more complex signatures also have to be introduced.
Thus, universes in type theory are needed so that any expression has a certain type. In some varieties of type theory, universes are used for another purpose: to distinguish between varieties of types. We have already seen that sets and statements are special cases of types. This shows that it might make sense to introduce into the theory a separate Prop universe for statements and a separate hierarchy of Set i universes for sets. This is exactly the approach used in Calculus of Inductive Constructions - the theory on which the Coq system is based.
1.2 Examples of simplest inductive types and recursive functions
Consider Arend's definitions of the simplest inductive data types: Boolean type, natural number type, and polymorphic lists. Arend uses the
\data
keyword to introduce new inductive types.
\data Empty -- ,
\data Bool
| true
| false
\data Nat
| zero
| suc Nat
\data List (A : \Set)
| nil
| \infixr 5 :-: A (List A)
As you can see from the examples above, after the
\data
keyword, you need to specify the name of the inductive type and a list of its constructors. At the same time, the data type and constructors may have some parameters. Let's say in the example above the
List
type has one parameter
A
The
nil
list constructor has no parameters, and the constructor: -: has two parameters (one of which is of type
A
, and the other is of type
List A
). The
\Set
universe consists of types that are sets (the definition of sets will be given in the next section). The
\infixr
allows you to use infix notation for the constructor: -: and, in addition, tells the Arend parser that the operator: -: is a right-associative operation with priority 5.
In Arend, all keywords begin with a backslash character (“\”), an implementation inspired by LaTeX. Just note that the lexical rules in Arend are very liberal:
Circle_HSpace, contrFibers=>Equiv, suc/=0, zro_*-left
and even
n:Nat
- all these literals are examples of valid identifiers in Arend. The final example shows how important it is for the Arend user to remember to put spaces between identifiers and colon characters . Note that in Arend identifiers it is not allowed to use Unicode characters (in particular, you cannot use Cyrillic).
Arend uses the
\func
keyword to define functions. The syntax of this construction is as follows: after the
\func
keyword, you need to specify the name of the function, its parameters and the type of the return value. The final element in defining a function is its body.
If it is possible to explicitly specify the expression in which the given function is to be calculated, then token => is used to indicate the body of the function. Consider, for example, the definition of a type negation function.
\func Not (A : \Type) : \Type => A -> Empty
The return type of a function does not always have to be specified explicitly. In the example above, Arend would be able to independently infer the type
Not
, and we could omit the expression “:
\Type
” after the brackets.
As in most formalized mathematics systems, the user does not have to indicate an explicit predictive level for the
\Type
universe, and definitions in which universes are used without explicitly specifying a predictive level are considered to be polymorphic .
Now let's try to define a function that calculates the length of the list. Such a function is easy to determine through pattern matching. Arend uses the
\elim
keyword for this. After it, you must specify the variables by which the comparison is performed (if there are more than one such variable, then they should be written with a comma). If the comparison is performed for all explicit parameters, then
\elim
along with the variables can be omitted. This is followed by a block of points of comparison, separated from each other by a vertical bar "|". Each item in this block is an expression of the form
«, » => «»
.
\func length {A : \Set} (l : List A) : Nat | nil => 0 | :-: x xs => suc (length xs)
In the example above, parameter A of the
length
function is surrounded by curly braces. These brackets in Arend are used to denote implicit arguments, i.e. arguments that the user can omit when calling a function or using a type. Note that in Arend you cannot use infix notation to designate constructors when matching with a pattern, so the prefix notation is used in the sample example.
As in Coq / Agda, in Arend all functions must be guaranteed to be completed (i.e., termination checking is present in Arend). In the definition of the length function, this check is successful, because a recursive call strictly reduces the first explicit argument. If such a reduction did not occur, Arend would issue an error message.
\func bad : Nat => bad [ERROR] Termination check failed for function 'bad' In: bad
Arend allows circular dependencies and mutually recursive functions for which completion checks are also performed. The algorithm of this check is implemented based on the article by A. Abel. In it you will find a more detailed description of the conditions that mutually recursive functions must satisfy.
1.3 How do sets differ from statements?
We previously wrote that examples of types are sets and statements. In addition, we used the keywords
\Type
and
\Set
to denote universes in Arend. In this section, we will try to explain in more detail how the statements differ from sets in terms of varieties of the intensional type theory (MLTT, CIC, HoTT), and at the same time explain what the meaning of the keywords
\Prop
,
\Set
and
\Type
in Arend consists of.
Recall that in the classical Martin-Löf theory there is no separation of types into sets and statements. In particular, in theory there is only one cumulative universe (which is denoted either by Set in Agda, or Type in Idris, or Sort in Lean). This approach is the simplest, but there are situations in which its shortcomings are manifested. Suppose we are trying to implement the "ordered list" type as a dependent pair consisting of a list and proof of its ordering. It turns out that then, in the framework of the “pure” MLTT, it will not be possible to prove the equality of ordered lists consisting of identical elements, which at the same time differ in terms of proof of ordering. To have such equality would be very natural and desirable, so the impossibility of proving it can be considered as a theoretical flaw in MLTT.
In Agda, this problem is partially solved with the help of so-called annotations of immateriality (see the source , in which the list example is discussed in more detail). These annotations, however, are not a construct from the MLTT theory, nor are they complete constructs on types (it is impossible to mark with a type annotation that is not used in the function argument).
In CIC, based on CIC, there are two different universes nested into each other:
Prop
(the universe of statements) and
Set
(the universe of sets), which are immersed in the comprehensive hierarchy of
Type
universes. The main difference between
Prop
and
Set
is that there are a number of restrictions on variables whose type belongs to
Prop
in Coq. For example, they cannot be used in calculations, and comparison with the sample for them is possible only inside the evidence of other statements. On the other hand, all elements of the type belonging to the
Prop
universe are equal in the axiom of inconsequential evidence, see the statement in Coq.Logic.ProofIrrelevance . Using this axiom, we could easily prove the equality of the ordered lists mentioned above.
Finally, consider Arend / HoTT's approach to statements and universes. The main difference is that HoTT dispenses with the axiom of inconsequential evidence. That is, there is no special axiom in HoTT that postulates that all elements of statements are equal. But in HoTT, a type, by definition , is a statement if it can be proved that all its elements are equal to each other. We can define a predicate on types that is true if the type is a statement:
\func isProp (A : \Type) => \Pi (aa' : A) -> a = a'
The question arises: what types satisfy this predicate, that is, are statements? It is easy to verify that this is true for empty and singleton types. For types where there are at least two different elements, this will no longer be true.
Of course, we want all the necessary logical connectives to be defined over the statements. In Section 1.1, we already discussed how they could be determined using type-theoretic constructions. There is, however, the following problem: not all of the operations we have entered retain the
isProp
property. Constructions of the product of types and the (dependent) functional type preserve this property, while constructions of the sum of types and dependent pairs do not. Thus, we cannot use the disjunction and the quantifier of existence.
This problem can be solved using the new design, which is added to HoTT, the so-called propositional truncation . This design allows you to turn any type into a statement. It can be considered as a formal operation, making equal all terms that inhabit this type. This operation is somewhat similar to annotations of immateriality from Agda, however, unlike them, it is a full-fledged operation on types with signature
\Type -> \Prop
.
The last important example of statements is the equality of two elements of some type. It turns out that in the general case the type of equality
a = a'
does not have to be a statement. The types for which it is one are called sets:
\func isSet (A : \Type) => \Pi (aa' : A) -> isProp (a = a')
All types that are found in ordinary programming languages satisfy this predicate, that is, equality on them is a statement. For example, this is true for natural numbers, integers, products of sets, sums of sets, functions over sets, lists of sets, and other inductive data types constructed from sets. This means that if we are only interested in such familiar constructions, then we can not think about arbitrary types that do not satisfy this predicate. All types found in Coq are sets .
Types that are not sets become useful if you want to deal with the homotopy type theory. For now, we simply refer the reader to the standard library module containing the definition of an n-dimensional sphere , an example of a type that is not a set.
Arend has special universes
\Prop
and
\Set
, consisting of statements and sets, respectively. If we already know that type A is contained in the
\Prop
(or
\Set
) universe, then a proof of the corresponding
isProp
(or
isSet
)
isSet
in Arend can be obtained using
Path.inProp
axiom built into the prelude (we give an example of using this axiom in section 2.3).
\func inProp {A : \Prop} : \Pi (aa' : A) -> a = a'
We have already noted that not all natural constructs on types retain the
isProp
property. For example, inductive data types with two or more constructors never satisfy it. As noted above, we can use the propositional truncation construct that turns any type into a statement.
In the Arend library, the standard implementation of propositional truncation is called
Logic.TruncP
. We could define a type of logical “or” in Arend as truncating the sum of types:
\data \fixr 2 Or (AB : \Type) -- Sum of types; analogue of Coq's type "sum" | inl A | inr B \func \infixr 2 || (AB : \Type) => TruncP (sum AB) -- Logical “or”, analogue of Coq's type "\/"
In Arend, there is another, simpler and more convenient way to define a propositionally truncated inductive type. To do this, just add the
\truncated
keyword before defining the data type. For example, the definition of a logical “or” in the Arend standard library is given as follows.
\truncated \data \infixr 2 || (AB : \Type) : \Prop -- Logical “or”, analogue of Coq's type "\/" | byLeft A | byRight B
Further work with propositionally truncated types resembles that of types assigned to the
Prop
universe in Coq. For example, pattern matching of a variable whose type is a statement is allowed only in a situation where the type of the expression being defined is itself a statement. Thus, it is always easy to define the function
Or-to-||
through comparison with the sample, but the inverse function to it, only if the type A
`Or`
B is a statement (which is rare enough, for example, when types
A
and
B
are both statements and mutually exclusive of each other).
\func Or-to-|| {AB : \Prop} (a-or-b : A `Or` B) : A || B | inl a => byLeft a | inr b => byRight
Recall also that the peculiarity of the mechanism of universes in Coq is that if some definition was assigned to the
Prop
universe, then in no way will it be possible to use it in the calculation. For this reason, Coq developers themselves do not recommend the use of propositional constructions, but advise to replace them with analogues from the universe of sets, if possible. The mechanism of Arend universes does not have this drawback, that is, in certain situations it is possible to use statements in calculations. We will give an example of such a situation when we discuss the implementation of the list sorting algorithm.
1.4 Classes in Arend
Since our goal is to implement the simplest sorting algorithm, it seems useful before that to familiarize yourself with the implementation of ordered sets available in the Arend standard library.
In Arend, classes are used to encapsulate operations and axioms that define mathematical structures, and also to highlight the relationships between these structures using inheritance. Classes are also namespaces, inside of which it is convenient to place constructions and theories that are appropriate in meaning.
The base class from which all order classes in Arend are inherited is the
BaseSet
class, which does not contain any members other than the designation
E
for the host set (that is, sets on which
BaseSet
descendant
BaseSet
already introduce various operations). Consider the definition of this class from the Arend standard library.
\class BaseSet (E : \Set) -- ,
In the definition above, carrier
E
declared as a class parameter. One may ask, is there a difference in the above
BaseSet
definition from the following definition, in which media E is defined as a class field?
\class BaseSet' -- | E : \Set
A slightly unexpected answer is that in Arend there is no difference between the two definitions in the sense that any class parameter (even implicit) in Arend is, in fact, its field. Thus, for both
BaseSet
implementations, one could use the
xE
expression to access the field E.
BaseSet
still a difference between the above variants of the
BaseSet
definition, but it is more subtle, we will examine it in more detail in the next section when we discuss class instances ( class instances).
The operation of sorting a list makes sense only if a linear order is specified on the type of objects in the list, so we first consider the definitions of a strict partially ordered set and a linearly ordered set.
\class StrictPoset \extends BaseSet { | \infix 4 < : E -> E -> \Prop | <-irreflexive (x : E) : Not (x < x) | <-transitive (xyz : E) : x < y -> y < z -> x < z } \class LinearOrder \extends StrictPoset { | <-comparison (xyz : E) : x < z -> x < y || y < z | <-connectedness (xy : E) : Not (x < y) -> Not (y < x) -> x = y }
From the point of view of type theory, classes in Arend can be considered analogs of sigma types with a more convenient syntax for projections and constructors.More precisely, any Arend class can be considered as a sigma type, the components of which are all unrealized fields of the class.
If the field type is a statement, then such a field is called a property . Properties differ from fields in that their implementations are never evaluated. For example, in StrictPoset field
<-irreflexive
and
<-transitive
are properties and the field
E
, and
<
- no. Properties give a noticeable increase in productivity, since their implementations (which, in fact, are proofs of these properties) are often large, but it usually makes no sense to calculate them.
To implement the sorting algorithm, it is not enough to have an ordered set; you also need to know that this order is decidable. The fact is that Arend usesconstructive mathematics , which means that not all predicates in it are decidable. In particular, equality of elements is not solvable for any type. For example, this is true for integers, but not for many functions over integers, since it is impossible to algorithmically determine whether two functions are equal or not. We can define a class of sets with decidable equality as follows:
\class DecSet \extends BaseSet | decideEq (xy : E) : Dec (x = y)
A predicate is
Dec
defined over statements in a way that
Dec E
is true if and only if it is
E
decidable, that is, when either
E
or negation is true
E
.
\data Dec (E : \Prop) | yes E | no (Not E)
Finally, consider the class
Dec
(from the word decidable) from the module
Order.LinearOrder
. The class Dec implements solvable linear orders, and, in particular, contains the axiom we need
trichotomy
, meaning that any two elements of the type
E
are comparable with respect to order <. Thus,
Dec
it can be considered as an analogue of the Comparable interface from Java.
\class Dec \extends LinearOrder, DecSet { | trichotomy (xy : E) : (x = y) || (x < y) || (y < x) | <-comparison xyz x<z => {?} -- | <-connectedness xyx/<yy/<x => {?} | decideEq xy => {?} }
The name of the class
Dec
coincides with the name of the data type already introduced above
Dec
, however, an apparent designation conflict does not actually occur, since the standard library contains this class in a different namespace. We will use
Dec
it to designate the class, and not the data type of the same name.
Axioms of linear order follow from the axioms of trichotomy, so it’s logical to immediately check these axioms inside the class
Dec
(in the listing above we omitted this evidence for brevity). The example
Dec
shows that in Arend multiple inheritance is allowed (
Dec
at the same time it is a descendant of
LinearOrder,
and
DecSet
), moreover, even diamond inheritance is allowed.
For rhomboid inheritance, there is the following natural restriction: the same field can be implemented in two different ancestors only if these implementations coincide (or if the field is a property, since the implementation is ignored in this case).
If you select a class
Dec
in the module
Order.LinearOrder
and ask IDEA to show the class hierarchy (usually this is done by pressing [Ctrl] + [H]), you get a tree similar to the picture below.

At this point, we suggest that you independently study the full class hierarchy of the Arend standard library (for this, just ask IDEA to show all subtypes
BaseSet
). As you can see, this hierarchy is now very extensive.
1.5 Class instances, type casts, classifier fields, and operator overloading.
Now let's try to create an instance of a strict order class
StrictPoset
for the type of natural numbers Nat. In Arend, you can create an instance of a class only for classes that have all the fields implemented. If we follow the analogy between classes and sigma types, then the class whose all fields are implemented corresponds to an empty sigma type (i.e., a singleton type), and creating an instance of the class corresponds to taking the only value of this singleton type.
We begin by defining the order and evidence of its simplest properties: antireflexivity and transitivity. Both of these properties are easily proved by induction by comparison with the sample.
data \infix 4 < (ab : Nat) \with | zero, suc _ => zero<suc_ | suc a, suc b => suc<suc (a < b) \lemma irreflexivity (x : Nat) (p : x < x) : Empty | suc a, suc<suc a<a => irreflexivity a a<a \lemma transitivity (xyz : Nat) (p : x < y) (q : y < z) : x < z | zero, suc y', suc z', zero<suc_, suc<suc y'<z' => zero<suc_ | suc x', suc y', suc z', suc<suc x'<y', suc<suc y'<z' => suc<suc (transitivity x' y' z' x'<y' y'<z')
In the examples above, instead of the keyword,
\func
we used
\lemma
. Lemmas relate to functions in the same way that class properties relate to class fields, that is, expressions for them are never evaluated, and this gives a performance boost. As with class properties, the keyword
\lemma
can only be used if the type of the result of the function belongs to the universe
\Prop
.
In the example above
x'<y'
- a clear name for the sample variable, which is a proof of inequality
x' < y'
. We will continue to use similar names for sample variables (i.e. names that match the record without spaces of statements, which these variables are proof of).
Now we can create an instance of the class
StrictPoset
. Arend has several different syntax options for this. The first way to instantiate a class is to use a keyword
\new
inside any expression. In this case, an “anonymous class instance” will be created.
\func NatOrder => \new StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity }
An expression
StrictPoset { … }
also makes sense without a keyword
\new
: in this case, it denotes an anonymous extension class
StrictPoset
. It is not necessary to implement all fields in anonymous extension classes, however, as mentioned above, the operation
\new
cannot be applied to an incompletely implemented class . A view expression
\new C { … }
has a type
C { … }
. Since this type is a descendant of C, it also has type C. Accordingly, in the example above it is true that it
NatOrder
is an instance of the class
StrictPoset
.
We have already noted above that class fields are no different from class parameters. In particular, from the point of view of internal representation, expression
StrictPoset Nat
is no different from expression
StrictPoset { | E => Nat }
. Note that we could indicate the type of function
NatOrder
as
StrictPoset
, and this would not be considered a mistake due to the usual rules of subtyping (a class descendant can be used instead of a parent).
An alternative way to define an instance of a class
NatOrder
is to use a keyword
\cowith
in the function header (in this case, the type of the function must be specified and be some kind of class).
\func NatOrder : StrictPoset \cowith { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity }
Finally, let's look at another way to define an instance of a class using the keyword.
\instance.
\instance NatOrder : StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity }
Arend implements an algorithm for finding class instances, similar to that in the Haskell language. The implementation of the function
NatOrder
through the keyword is
\instance
similar to the implementation through
\cowith
and differs from it only in that this function will be used during the search for instances of the class
StrictPoset
(we will discuss instances just below).
Recall that in the implementation
BaseSet
from the standard library, the carrier set E is defined as a class parameter (and not as a field), and in the last section we said that such an implementation has some difference from the implementation of E as a class field. Now we will comment on this difference in more detail.
We mentioned that class parameters from the point of view of Arend’s internal implementation are no different from class fields. However, Arend has an agreement that the first explicit class argument is not converted by default to a so-called class field, but to a so-called classifier field (this convention works if the " classifier field " is not explicitly selected by the user with a keyword
\classifying \field
, a class in Arend may have only one classifier field). Classifying class fields have the following properties:
- Arend can implicitly cast instances of a class to the type of its classifier by referring to the corresponding projector. For example, if it
X
has a typeStrictPoset
, then the expression isList X
completely correct and matches the value of the expressionList XE
.
- Arend .
Let us first explain why instances are needed at all. Suppose that we have implemented through a construction with a keyword
\instance
several instances of the class
StrictPoset
for various data types, for example, for natural numbers
Nat
and integers
Int
(we will call constructed instances
NatOrder
and
IntOrder
).
It is argued that now it is possible to use notation
x < y
to indicate order, both in the case where x, y are natural numbers, and in the case where x, y are integers. In the first case, Arend will automatically determine what is meant
NatOrder.<
, and in the second -
IntOrder.<
.
We now explain in more detail how the instance search algorithm works. Arend determines that the <field is entered in the class
StrictPoset
, in which the field E is declared as the classifying field. Next, Arend calculates the type of arguments of the expression
x<y
and tries to find in the current scope the instance of the class
StrictPoset
(or its descendant) in which the classifying field E is of the desired type. If such an instance is found, then the implementation of the field
<
is taken from this instance.
Note that automatic conversion of a class to a type of its classifying field is just a special case of a more general type conversion mechanism in Arend. To allow implicitly casting one type to another, you need to use a special design
\use \coerce
inside the associated module of this definition. In Arend, each definition has a so-called associated module.- some namespace used to place various auxiliary constructions in it. To add any other definitions to the associated definition module, the keyword is used
\where
.
Consider the simplest example of using a type conversion mechanism. The function
fromNat
will be used to implicitly convert natural numbers to integers.
\data Int | pos Nat | neg Nat \with { zero => pos zero } \where { \use \coerce fromNat (n : Nat) => pos n }
The syntax for the declaration is
\use \coerce
similar
\func
with the difference that this function should have only one explicit argument. In this case, either the type of the result or the type of a single argument of the function must coincide with the definition with which the given module is associated (of course, this is possible only for modules associated with the definitions of classes or inductive data types).
Posted by Sergey Sinchuk, Senior Researcher , HoTT Group and Dependent Types at JetBrains Research.
All Articles