How I created a filter that does not corrupt the image even after a million runs
Having completed the creation of web architecture for our new web comic Meow the Infinite , I decided it was time to write some long overdue technical articles. This article will focus on a filter that I developed several years ago. It has never been discussed in the field of video compression, although it seems to me that it is worth doing.
In 2011, I developed the “half-pel filter”. This is a special kind of filter that takes an incoming image and most convincingly displays how the image would look when shifted exactly half a pixel .
You are probably wondering why such a filter may be needed at all. In fact, they are quite common in modern video codecs. Video codecs use similar filters to take fragments of previous frames and use them in subsequent frames. Older codecs moved frame data only a whole pixel at a time, but the new codecs went further and allow a shift of half or even a quarter pixel to better transmit small movements.
When analyzing the behavior of motion compensation algorithms in traditional halfpel filters, Jeff Roberts found that when applied repeatedly to sequential frames, they quickly degrade, forcing other parts of the video compressor to use more data than necessary to correct artifacts. If you disable these corrections and look at the "raw" results of the halfpel filter, then this is the original image:

turns into this:

just after one second of video. As it should, it is shifted to the side, because each frame shifted the image by half a pixel. But the result does not look like a displaced version of the original image, it is seriously distorted.
During the "one second video" filter is actually applied many times - 60 if the video is played at a frequency of 60 frames per second. But ideally, we need filters that are resistant to such distortions. If we had them, smoothly scrolling videos would not have been encoded with so many artifact fixes, which would have made them less, or better, or both.
If you are familiar with the area of video compression, you may wonder why do we even need to use the halfpel filter more than once. In the end, if we apply the halfpel filter twice, then we’ll already move one whole pixel, so why not just use the data from two frames back and just take them ?
The answer is not so simple. Firstly, the more data we need to encode the data, the less compression we get. Therefore, if we start encoding without the need for too much data such as “from which frame to take data”, the video will not be compressed very well.
But this is not the most important. The main problem is that if we need to take information from previous frames, we will have to store them . To preserve the previous two frames, instead of one, you need to guess that you have twice as much memory. For modern CPUs, this is not a special problem, they have a lot of memory and such a trifle does not bother them. But this is a problem for you if you want to create a fast, portable, widely used video format that should work in devices with a small amount of memory (mobile phones, built-in electronics, etc.).
We really do not want to store several frames in order to compensate for the movement just so as not to use a halfpel filter. Therefore, I was instructed to find out what exactly is happening here, and to figure out if I can create a filter that does not have such problems.
Before that, I had never worked with filters and had no idea how they are usually developed. Oddly enough, it turned out to be in my favor, because I had to look at this problem without prejudice.
I quickly realized that the most popular halfpel filters have a similar structure: for each pixel in the output image, 2 to 8 pixels of the incoming image are taken, which are sampled and mixed with certain coefficients. Different filters differ only in the number of sampled source pixels (often in the jargon of filter developers they are called tap) and pixel mixing factors. These coefficients are often called the “filter kernel” and that’s all that is needed to fully describe the filter.
If you are familiar with any kind of sampling or resampling of images (for example, scaling images), then this should be clear to you. Essentially, filters do the same thing. Since video compression is a vast area in which various studies are carried out, it is obvious that there are many other ways to compensate for motion other than simple filtering. But common codecs usually use motion compensation procedures with halfpel filters, which are essentially identical to image scaling filters: they just take the original pixels, multiply them by some weights, add them up and get the output pixels.
So, we need to shift the image by half a pixel. If you are a graphics programmer, but are not particularly familiar with filtering, you might think: "I also have a problem, just use a bilinear filter." This is a standard process in working with graphics, when we need to calculate intermediate values between two incoming data elements, as happens here.
A bilinear filter for moving exactly half a pixel can be easily described by the following filter core:
This will work, but not without problems. If your goal is high-quality images, and in the case of video compression, the goal is just that, then a bilinear filter is not the best solution, because it adds more blur to the result than necessary. It is not so much , but more than other filters create.
To show this clearly, here is an approximate image of the walrus eye from the original image after a single application of the most common filters:

On the left is the original, on the right is bilinear filtering. Between them are the most widely used halfpel filters for video codecs. If you look closely, you can see that almost all images look similar, except for a bilinear one, which is slightly more blurry. Although there is not much blur, if your main goal is image quality, then this is enough to prefer a different filter to a bilinear filter.
So how do other filters “maintain” sharpness and avoid blurring? Let's remember what the core of bilinear blur looks like:
It is very simple. To shift the image by half a pixel, we take a pixel and mix it 50% with its neighbor. That's all. One can imagine how this “blurs” the image, because in those places where the bright white pixel is adjacent to the dark black, these two pixels are averaged during bilinear filtering, creating a gray pixel that “softens” the border. This happens with every pixel, so literally every area where there is a clear difference in color or brightness. smoothed out.
That is why in high-quality codecs bilinear filtering is not used for motion compensation (although it can be used in other cases). Instead, filters are used that preserve sharpness, for example, such:
As you can see, where bilinear filtering took into account only two pixels, these filters take into account six (h.264) or even eight (HEVC) pixels. In addition, they do not just calculate the usual weighted average values of these pixels, but use negative weights for some pixels to subtract these pixels from other values.
Why do they do it?
It is actually not difficult to understand this: using both positive and negative values, and also considering a wider “window”, the filter is able to take into account the difference between adjacent pixels and simulate the sharpness of the two nearest pixels relative to their farthest neighbors. This allows you to maintain the sharpness of the image result in those places where the pixels differ significantly from their neighbors, while averaging is still used to create believable values of “half-pixel” shifts, which must necessarily reflect the combination of pixels from the incoming image.
So, is the problem resolved? Yes, it is possible, but if you only need to do one half-pixel offset. However, these "sharpening" filters (and here I use this term intentionally) actually do something dangerous, essentially similar to what bilinear filtering does. They just better know how to hide it.
Where bilinear filtering reduces image sharpness, these standard filters increase it, like the sharpen operation in some kind of graphics program. The amount of sharpening is very small, so if we execute the filter only once, we will not notice this. But if filtering is performed several times, then this can become very noticeable.
And, unfortunately, since this sharpening is procedural and depends on the difference between the pixels, it creates a feedback loop that will continue to sharpen the same border over and over until it destroys the image. You can show this with specific examples.
Above - the original image, below - with bilinear filtering, performed over 60 frames:


As you might expect, blurring simply continues to reduce the sharpness of the image until it becomes quite blurry. Now, the original will be at the top, and the h.264 codec halfpel filter that will run for 60 frames at the bottom:


See all this rubbish? The filter did the same as the “blur” effect of bilinear filtering, but vice versa - it “sharpened the image” so much that all the parts where the details were turned into strongly distorted light / dark patterns.
Does the HEVC codec using 8 pixels behave better? Well, it definitely does better than h.264:

but if we increase the time from 60 frames (1 second) to 120 frames (2 seconds), we will still see that there is feedback and the image is destroyed:

For the sake of those who like signal processing, I’ll also add a windowed-sinc filter (called the Lanczos filter) for reference:
I will not explain in this article why someone might be interested in “windowed sinc”, but suffice it to say that this filter is popular for theoretical reasons, so look how it looks when processing 60 frames (1 second):

and when processing 120 frames (2 seconds):

Better than h.264, and about the same as HEVC.
How can we achieve better results than h.264, HEVC and windowed sinc? And how much better can they be?
I would expect to see similar questions in the literature on video compression and they should be well known to compression specialists, but in fact (at least for 2011) I did not find anyone who at least stated that this was a problem. So I had to come up with a solution alone.
Fortunately, the formulation of the problem is very simple: create a filter that can be applied as many times as possible so that the image looks approximately the same as at the beginning.
I call this definition “stable filtering” because, in my opinion, it can be considered a filter property. A filter is “stable” if it does not fall into its feedback loop, that is, it can be applied repeatedly without creating artifacts. The filter is "unstable" if it creates artifacts that are amplified by repeated use and eventually destroy the image.
I repeat, I do not understand why this topic is not considered in the literature on video codecs or image processing. Perhaps it uses a different terminology, but I have not met it. The concept of "feedback" is well established in the field of working with sound. but not an important issue in image processing. Perhaps because usually filters should be applied only once?
If I were a specialist in this field, then I most likely had an opinion on this subject, and perhaps I would even know those nooks of specialized literature where there are already solutions to this problem, known to few. But, as I said at the beginning of the article, I had never been able to create filters before, so I searched only in widely known articles (although it is worth noting that there is at least one person well known in the literature who also hasn’t heard anything like this )
So, in the morning they told me that we needed this filter, and all day I tried to create it. My approach was simple: I created a program that executed the filter hundreds of times and at the end produced an image so that I could see the result of lengthy runs. Then I experimented with different filter coefficients and observed the results. It was literally a directional trial and error process.
About an hour later, I picked up the best filter coefficients suitable for this task (but they had one flaw, which I will discuss in the second part of the article):
This core is on the verge of sharpening and blurring. Since sharpening always leads to feedback that creates vivid and obvious artifacts, this filter core prefers a bit of blur so that the image just looks a little more “dull”.
This is how it looks after 60 frames. For reference, I showed all the filters in this order: the original image (without filtering), my filter, bilinear, Lanczos, h.264, HEVC:






As you can see, my filter gives slightly more blurry results than sharpen filters, but does not have unacceptable sharpness artifacts after 60 frames. However, you may prefer blur artifacts to sharpen artifacts, so you can choose between the best sharpen filter (Lanczos) and mine. However, if we increase the number to 120 frames, then my filter is out of competition:






After 300 frames, all filters, except mine, become like a bad joke:


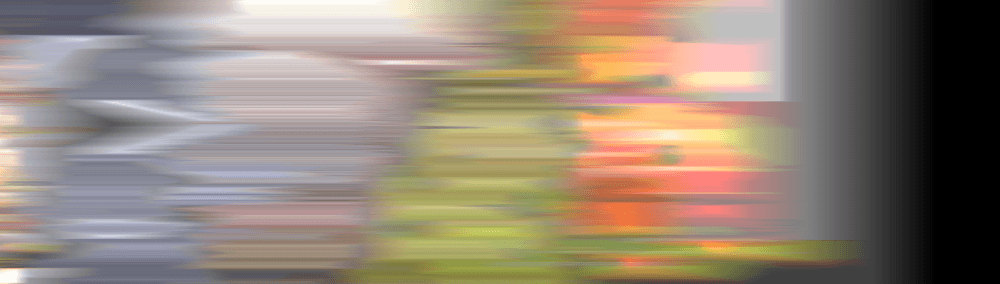


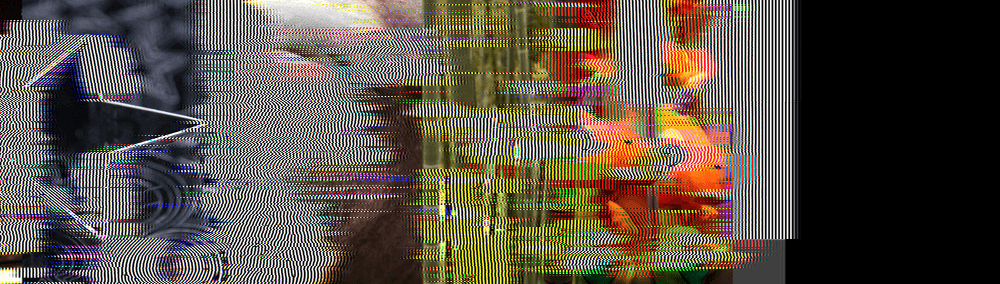
After 600 frames, the joke becomes even more cruel:



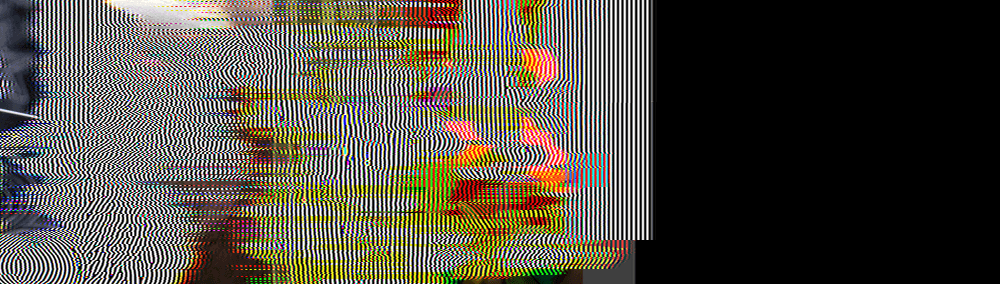


You don’t even have to say what happens after 900 frames:

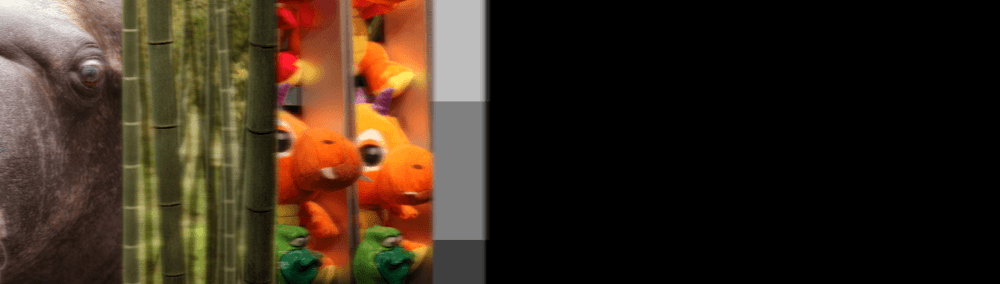

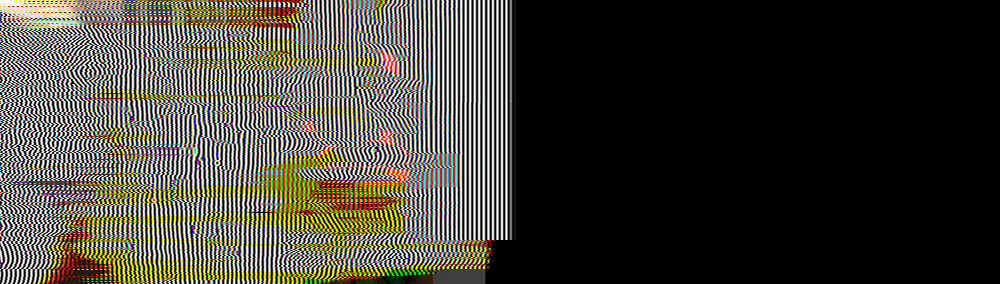
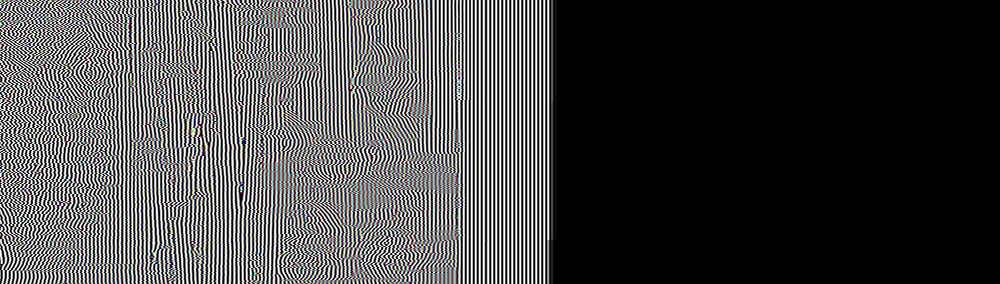

At this stage, one naturally wonders: is my filter really stable, or is it just a very slow blur, much slower than bilinear filtering? Perhaps after thousands of repetitions, my filter will gradually blur the image?
Surprisingly, the answer seems to be negative. Although a bit of blur is added over the course of about a hundred first overlays, it looks like the filter converges to a stable representation of the image, which then never degrades. Here is another enlarged image of a walrus eye:

From left to right: the original image, my filter applied 60 times, 120 times, 300 times, 600 and 900 times. As you can see, the blur converges to a stable state, which no longer degrades even after hundreds of filter overlays. For contrast, compare this with windowed sync for the same number of samples (tap), and see how poorly (and fast!) The artifacts form the feedback and create a useless result:

My filter seems very stable, and compared to all the filters I have seen, it produces the best results after repeated use. It seems that it has a certain “asymptotic” property, in which the data quickly converges to a (limited) smoothed image, and then this smoothed image is saved and does not perform unlimited degradation to complete garbage.
I even tried to apply the filter a million times, and it seems that after the first few hundred overlays it does not degrade further. Without a better mathematical analysis (and I have not yet found a mathematical solution that can prove it exactly, but I know for sure that it is somewhere), I cannot say with certainty that somewhere after billions or trillions of overlays that -it will not break. Within reasonable testing, I was not able to detect further degradation.
At this stage, it would be logical to ask the question: is this really the best that can be found? Intuition tells us that it’s not, because I had absolutely no knowledge about the development of filters and almost did not look into the literature, I picked up this filter in just an hour. At least it can be assumed that after such a brief study, I would not have found a definitively-best-all-conquering-great filter.
Is this assumption true? And if true, what will be the final best filter? I will discuss this in more detail in the second part of the article.
In 2011, I developed the “half-pel filter”. This is a special kind of filter that takes an incoming image and most convincingly displays how the image would look when shifted exactly half a pixel .
You are probably wondering why such a filter may be needed at all. In fact, they are quite common in modern video codecs. Video codecs use similar filters to take fragments of previous frames and use them in subsequent frames. Older codecs moved frame data only a whole pixel at a time, but the new codecs went further and allow a shift of half or even a quarter pixel to better transmit small movements.
When analyzing the behavior of motion compensation algorithms in traditional halfpel filters, Jeff Roberts found that when applied repeatedly to sequential frames, they quickly degrade, forcing other parts of the video compressor to use more data than necessary to correct artifacts. If you disable these corrections and look at the "raw" results of the halfpel filter, then this is the original image:

turns into this:

just after one second of video. As it should, it is shifted to the side, because each frame shifted the image by half a pixel. But the result does not look like a displaced version of the original image, it is seriously distorted.
During the "one second video" filter is actually applied many times - 60 if the video is played at a frequency of 60 frames per second. But ideally, we need filters that are resistant to such distortions. If we had them, smoothly scrolling videos would not have been encoded with so many artifact fixes, which would have made them less, or better, or both.
If you are familiar with the area of video compression, you may wonder why do we even need to use the halfpel filter more than once. In the end, if we apply the halfpel filter twice, then we’ll already move one whole pixel, so why not just use the data from two frames back and just take them ?
The answer is not so simple. Firstly, the more data we need to encode the data, the less compression we get. Therefore, if we start encoding without the need for too much data such as “from which frame to take data”, the video will not be compressed very well.
But this is not the most important. The main problem is that if we need to take information from previous frames, we will have to store them . To preserve the previous two frames, instead of one, you need to guess that you have twice as much memory. For modern CPUs, this is not a special problem, they have a lot of memory and such a trifle does not bother them. But this is a problem for you if you want to create a fast, portable, widely used video format that should work in devices with a small amount of memory (mobile phones, built-in electronics, etc.).
We really do not want to store several frames in order to compensate for the movement just so as not to use a halfpel filter. Therefore, I was instructed to find out what exactly is happening here, and to figure out if I can create a filter that does not have such problems.
Before that, I had never worked with filters and had no idea how they are usually developed. Oddly enough, it turned out to be in my favor, because I had to look at this problem without prejudice.
The basics
I quickly realized that the most popular halfpel filters have a similar structure: for each pixel in the output image, 2 to 8 pixels of the incoming image are taken, which are sampled and mixed with certain coefficients. Different filters differ only in the number of sampled source pixels (often in the jargon of filter developers they are called tap) and pixel mixing factors. These coefficients are often called the “filter kernel” and that’s all that is needed to fully describe the filter.
If you are familiar with any kind of sampling or resampling of images (for example, scaling images), then this should be clear to you. Essentially, filters do the same thing. Since video compression is a vast area in which various studies are carried out, it is obvious that there are many other ways to compensate for motion other than simple filtering. But common codecs usually use motion compensation procedures with halfpel filters, which are essentially identical to image scaling filters: they just take the original pixels, multiply them by some weights, add them up and get the output pixels.
The need for "sharpness"
So, we need to shift the image by half a pixel. If you are a graphics programmer, but are not particularly familiar with filtering, you might think: "I also have a problem, just use a bilinear filter." This is a standard process in working with graphics, when we need to calculate intermediate values between two incoming data elements, as happens here.
A bilinear filter for moving exactly half a pixel can be easily described by the following filter core:
// NOTE(casey): Simple bilinear filter BilinearKernel[] = {1.0/2.0, 1.0/2.0};
This will work, but not without problems. If your goal is high-quality images, and in the case of video compression, the goal is just that, then a bilinear filter is not the best solution, because it adds more blur to the result than necessary. It is not so much , but more than other filters create.
To show this clearly, here is an approximate image of the walrus eye from the original image after a single application of the most common filters:

On the left is the original, on the right is bilinear filtering. Between them are the most widely used halfpel filters for video codecs. If you look closely, you can see that almost all images look similar, except for a bilinear one, which is slightly more blurry. Although there is not much blur, if your main goal is image quality, then this is enough to prefer a different filter to a bilinear filter.
So how do other filters “maintain” sharpness and avoid blurring? Let's remember what the core of bilinear blur looks like:
BilinearKernel[] = {1.0/2.0, 1.0/2.0};
It is very simple. To shift the image by half a pixel, we take a pixel and mix it 50% with its neighbor. That's all. One can imagine how this “blurs” the image, because in those places where the bright white pixel is adjacent to the dark black, these two pixels are averaged during bilinear filtering, creating a gray pixel that “softens” the border. This happens with every pixel, so literally every area where there is a clear difference in color or brightness. smoothed out.
That is why in high-quality codecs bilinear filtering is not used for motion compensation (although it can be used in other cases). Instead, filters are used that preserve sharpness, for example, such:
// NOTE(casey): Half-pel filters for the industry-standard h.264 and HEVC video codecs h264Kernel[] = {1.0/32.0, -5.0/32.0, 20.0/32.0, 20.0/32.0, -5.0/32.0, 1.0/32.0}; HEVCKernel[] = {-1.0/64.0, 4.0/64.0, -11.0/64.0, 40.0/64.0, 40/64.0, -11.0/64.0, 4.0/64.0, -1.0/64.0};
As you can see, where bilinear filtering took into account only two pixels, these filters take into account six (h.264) or even eight (HEVC) pixels. In addition, they do not just calculate the usual weighted average values of these pixels, but use negative weights for some pixels to subtract these pixels from other values.
Why do they do it?
It is actually not difficult to understand this: using both positive and negative values, and also considering a wider “window”, the filter is able to take into account the difference between adjacent pixels and simulate the sharpness of the two nearest pixels relative to their farthest neighbors. This allows you to maintain the sharpness of the image result in those places where the pixels differ significantly from their neighbors, while averaging is still used to create believable values of “half-pixel” shifts, which must necessarily reflect the combination of pixels from the incoming image.
Unstable filtering
So, is the problem resolved? Yes, it is possible, but if you only need to do one half-pixel offset. However, these "sharpening" filters (and here I use this term intentionally) actually do something dangerous, essentially similar to what bilinear filtering does. They just better know how to hide it.
Where bilinear filtering reduces image sharpness, these standard filters increase it, like the sharpen operation in some kind of graphics program. The amount of sharpening is very small, so if we execute the filter only once, we will not notice this. But if filtering is performed several times, then this can become very noticeable.
And, unfortunately, since this sharpening is procedural and depends on the difference between the pixels, it creates a feedback loop that will continue to sharpen the same border over and over until it destroys the image. You can show this with specific examples.
Above - the original image, below - with bilinear filtering, performed over 60 frames:


As you might expect, blurring simply continues to reduce the sharpness of the image until it becomes quite blurry. Now, the original will be at the top, and the h.264 codec halfpel filter that will run for 60 frames at the bottom:


See all this rubbish? The filter did the same as the “blur” effect of bilinear filtering, but vice versa - it “sharpened the image” so much that all the parts where the details were turned into strongly distorted light / dark patterns.
Does the HEVC codec using 8 pixels behave better? Well, it definitely does better than h.264:

but if we increase the time from 60 frames (1 second) to 120 frames (2 seconds), we will still see that there is feedback and the image is destroyed:

For the sake of those who like signal processing, I’ll also add a windowed-sinc filter (called the Lanczos filter) for reference:
// NOTE(casey): Traditional 6-tap Lanczos filter LanczosKernel[] = {0.02446, -0.13587, 0.61141, 0.61141, -0.13587, 0.02446};
I will not explain in this article why someone might be interested in “windowed sinc”, but suffice it to say that this filter is popular for theoretical reasons, so look how it looks when processing 60 frames (1 second):

and when processing 120 frames (2 seconds):

Better than h.264, and about the same as HEVC.
Stable filtering
How can we achieve better results than h.264, HEVC and windowed sinc? And how much better can they be?
I would expect to see similar questions in the literature on video compression and they should be well known to compression specialists, but in fact (at least for 2011) I did not find anyone who at least stated that this was a problem. So I had to come up with a solution alone.
Fortunately, the formulation of the problem is very simple: create a filter that can be applied as many times as possible so that the image looks approximately the same as at the beginning.
I call this definition “stable filtering” because, in my opinion, it can be considered a filter property. A filter is “stable” if it does not fall into its feedback loop, that is, it can be applied repeatedly without creating artifacts. The filter is "unstable" if it creates artifacts that are amplified by repeated use and eventually destroy the image.
I repeat, I do not understand why this topic is not considered in the literature on video codecs or image processing. Perhaps it uses a different terminology, but I have not met it. The concept of "feedback" is well established in the field of working with sound. but not an important issue in image processing. Perhaps because usually filters should be applied only once?
If I were a specialist in this field, then I most likely had an opinion on this subject, and perhaps I would even know those nooks of specialized literature where there are already solutions to this problem, known to few. But, as I said at the beginning of the article, I had never been able to create filters before, so I searched only in widely known articles (although it is worth noting that there is at least one person well known in the literature who also hasn’t heard anything like this )
So, in the morning they told me that we needed this filter, and all day I tried to create it. My approach was simple: I created a program that executed the filter hundreds of times and at the end produced an image so that I could see the result of lengthy runs. Then I experimented with different filter coefficients and observed the results. It was literally a directional trial and error process.
About an hour later, I picked up the best filter coefficients suitable for this task (but they had one flaw, which I will discuss in the second part of the article):
MyKernel[] = {1.0/32.0, -4.0/32.0, 19.0/32.0, 19.0/32.0, -4.0/32.0, 1.0/32.0};
This core is on the verge of sharpening and blurring. Since sharpening always leads to feedback that creates vivid and obvious artifacts, this filter core prefers a bit of blur so that the image just looks a little more “dull”.
This is how it looks after 60 frames. For reference, I showed all the filters in this order: the original image (without filtering), my filter, bilinear, Lanczos, h.264, HEVC:






As you can see, my filter gives slightly more blurry results than sharpen filters, but does not have unacceptable sharpness artifacts after 60 frames. However, you may prefer blur artifacts to sharpen artifacts, so you can choose between the best sharpen filter (Lanczos) and mine. However, if we increase the number to 120 frames, then my filter is out of competition:






After 300 frames, all filters, except mine, become like a bad joke:


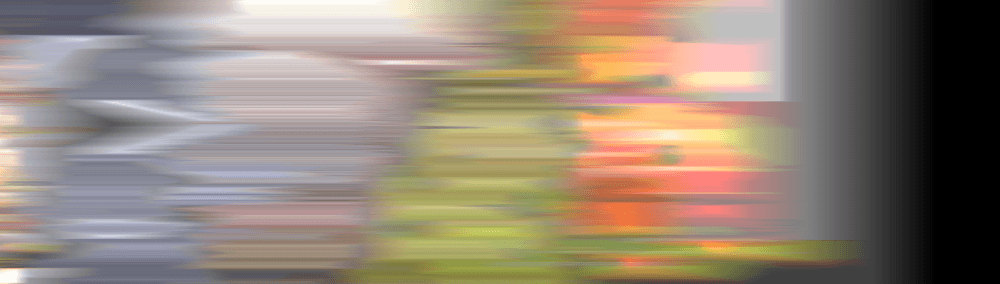


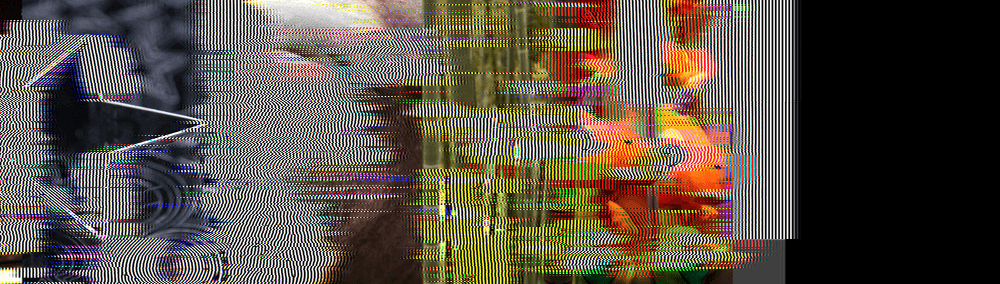
After 600 frames, the joke becomes even more cruel:



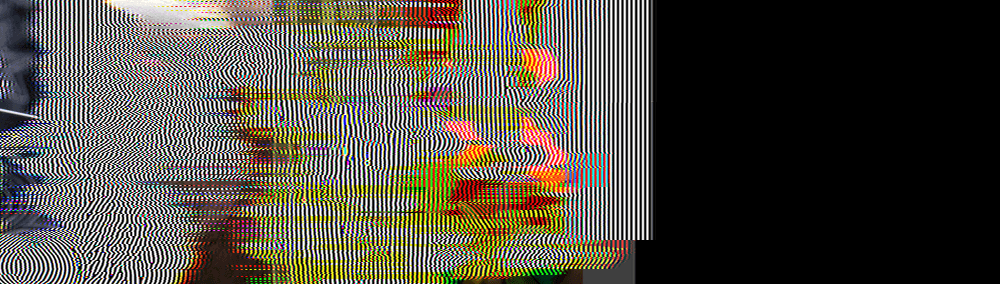


You don’t even have to say what happens after 900 frames:

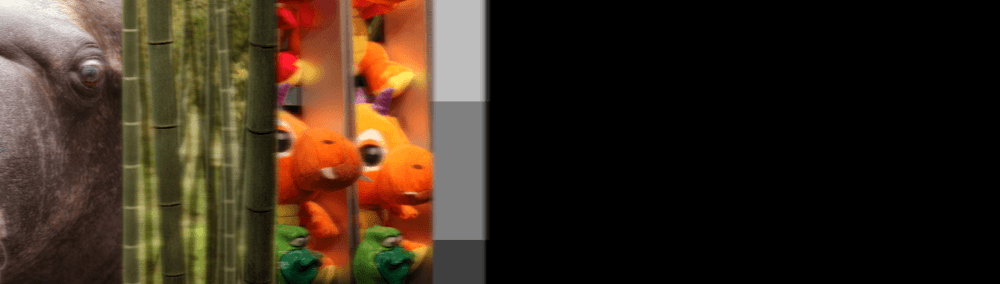

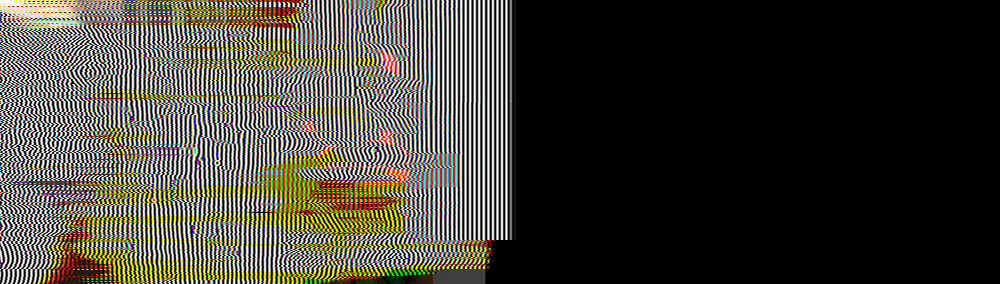
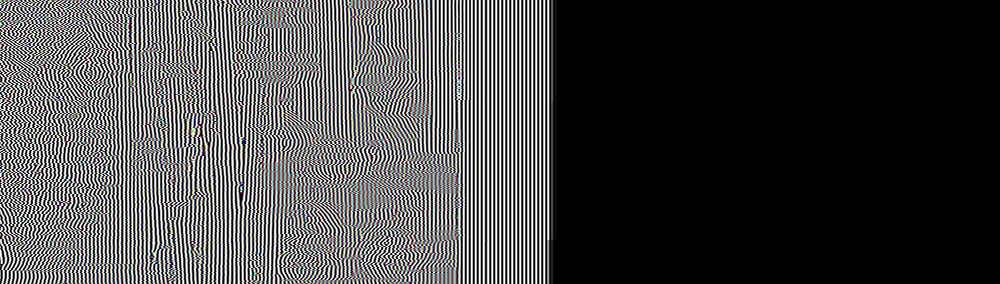

How stable is it?
At this stage, one naturally wonders: is my filter really stable, or is it just a very slow blur, much slower than bilinear filtering? Perhaps after thousands of repetitions, my filter will gradually blur the image?
Surprisingly, the answer seems to be negative. Although a bit of blur is added over the course of about a hundred first overlays, it looks like the filter converges to a stable representation of the image, which then never degrades. Here is another enlarged image of a walrus eye:

From left to right: the original image, my filter applied 60 times, 120 times, 300 times, 600 and 900 times. As you can see, the blur converges to a stable state, which no longer degrades even after hundreds of filter overlays. For contrast, compare this with windowed sync for the same number of samples (tap), and see how poorly (and fast!) The artifacts form the feedback and create a useless result:

My filter seems very stable, and compared to all the filters I have seen, it produces the best results after repeated use. It seems that it has a certain “asymptotic” property, in which the data quickly converges to a (limited) smoothed image, and then this smoothed image is saved and does not perform unlimited degradation to complete garbage.
I even tried to apply the filter a million times, and it seems that after the first few hundred overlays it does not degrade further. Without a better mathematical analysis (and I have not yet found a mathematical solution that can prove it exactly, but I know for sure that it is somewhere), I cannot say with certainty that somewhere after billions or trillions of overlays that -it will not break. Within reasonable testing, I was not able to detect further degradation.
Is it the best stable Halfpel filter for six tap s?
At this stage, it would be logical to ask the question: is this really the best that can be found? Intuition tells us that it’s not, because I had absolutely no knowledge about the development of filters and almost did not look into the literature, I picked up this filter in just an hour. At least it can be assumed that after such a brief study, I would not have found a definitively-best-all-conquering-great filter.
Is this assumption true? And if true, what will be the final best filter? I will discuss this in more detail in the second part of the article.
All Articles