Just division, or how to create a mathematical theory and earn $ 400K on it. Series Three, Final
In previous series, we looked at fractional numbers from several unusual angles. In this series, after the introduction and some theoretical basis , we will try to collect everything in a convenient form and benefit from the available information.
Having talked about the properties of the table of residuals, we can try to apply knowledge about it to earning. So many in the world find it useful to search for large primes. And even there are organizations that are ready to give a lot of money to someone who finds a large prime number. But the topic of quantum computing is also popular in the world. Why? Because it promises to hack a well-known cryptosystem. This, so to speak, is the advertising slogan of quantum computing, which allows convincing any decision-making manager to allocate money for such an interesting lesson. Therefore, we will talk about this topic.
First we’ll show you how to look for prime numbers. The main problem here is quantity. For large numbers, there are simply no algorithms that allow you to quickly check whether a prime number is in front of us or a compound one. Therefore, the maximum downtime for today is less than 25 million decimal places in length. This is only 10 megabytes, on such arrays modern processors show millisecond processing times, but to check whether a prime number is in our array, a modern processor will consume electricity and buzz with a fan for decades. That is, technically, the size for the processor is small, but the number of operations in known algorithms for such large numbers is simply huge. Why is this situation?
For simplicity tests, for example, enumeration of dividers is used. But how many divisors do you need to iterate over for a number ten megabytes long? The answer is that even atoms with electrons in the entire universe will be enough only for a tiny part of this value. That is, we need huge numbers of universes, just to place all these divisors there. Too much? Therefore, enumeration of divisors for ten-megabyte numbers is applied to a limited extent (yes, the universe let us down ...), but fortunately there are other algorithms. We can distinguish algorithms that do not use enumeration of divisors, and at the same time they are guaranteed to give an answer - simple in front of us or composite. But these are very slow algorithms. That is, they, of course, are capable of grinding numbers a hundred or two hundred bits that way, but ten megabytes for them is death all at once. Therefore, you have to get out the tricky ways.
But the problem with all the tricks is that they have not yet come up with a complete theory of divisibility. After all, if it were complete, we would very quickly find the answer - a prime or not. More precisely, a theory would quickly give us an algorithm for testing that would not keep us waiting until the thermal death of the universe. That's why they give bonuses to those who come up with an algorithm as quickly as possible, and, best of all, a whole theory to provide algorithms for all occasions.
In the meantime, we have at our disposal a specific Luc-Lemer test, which uses the connection of very specific Mersenne numbers with a certain sequence, but not the remainder of the division, as we recently observed, but the sums of the degrees of some irrational numbers. That is, the simplicity test was performed from the side, let's say, not quite obvious, although some here can pick up more complicated comparisons. But why were the degrees of irrational numbers closer to simplicity tests than all other advances in number theory? Apparently because mathematics does not know simple solutions. And as a result, a method was used, although not an obvious but still working, from the region not closest to integer calculations, approximately how the transition from Cartesian to polar coordinates helps to use additional methods that are very difficult to implement in Cartesian coordinates.
In addition to the Luke-Lemer test, there are also probabilistic tests. They help weed out guaranteed compound numbers. So one of the actively used probabilistic tests is a test based on the Fermat formula, which we recently spoke about. How does he work? Very simple - remember the column of units on the right in the remainder table? This is a guaranteed sign of the simplicity of a number. To explain the verification using Fermat’s formula, mathematicians use specific terminology that few people understand except for them, so we won’t go into these mathematical jungles, but explain everything on the fingers, or rather, from the table of residuals. To understand what the remainder will be in the last column, you need to either divide by a column and reach the remainder at the position containing 1 in it, or calculate this remainder using the formula that allows you to get the remainder by the position number and the base of the number system. The first option for numbers ten megabytes long will require almost infinite time, because the width of the table is N-1, which means that for a number of the order of a million, the table will have a minimum of a million columns. For a billion, a billion. For a trillion, a trillion. But a trillion, it's only 12 decimal places. And we are interested in a number in which under 25 million characters. Even a trillion residues by the method of dividing the column we have to calculate hardly less than half an hour, and this is only 12 decimal places. Total! Compared to 25 million. Do you think you have enough time to wait for the result in this way? That is why it is better to immediately calculate the desired value using the formula. And just the Fermat formula corresponds to the formula for calculating the remainder in the last position in the table. Moreover, if the period is shorter than the width of the table, then mathematics does not yet know how to calculate it, which means that in any case, we need to choose the last column. The mathematicians in the test simply check whether the remainder in the last column is equal to one for the number system they have chosen (although mathematicians do not use the concept of the number system, for them there is only a basis raised to a power). If the remainder is not equal to one, the number is guaranteed to be composite. As we saw in the example of the table for the number 21, it is the absence of a unit at the end of many lines that distinguishes it from the tables for primes. But there is one problem. There may still be units in some lines, which we could also verify just by the example of the table for 21. That is why mathematicians call the test based on the Fermat formula probabilistic. That is, they do not know if the number is prime if the Fermat test found a remainder equal to one, because such false units are in the table for the number 21, and in many other tables, even for ten megabyte numbers. So you need to either check all the lines in a row, which is a very long time, because the lines for a ten-megabyte number, as noted earlier, are much more than everything in the universe we know, or just say - it is likely that this number is prime. Here is the last method and mathematicians have chosen. Fortunately, there are few lines ending with a unit in most composite numbers. True, there are also the so-called Carmichael numbers, in which all lines, except multiples of the divisors of such a number, end by one. So, on the Carmichael numbers, the probabilistic test by the Fermat formula is practically guaranteed to be wrong, because to eliminate the error you need to get into a multiple of the number divisor, and there can be only two divisors in the ten-megabyte number, and their value can be very large, and therefore the probability of getting exactly in such a line with a random choice of the base of the number system is practically zero. But on the other hand, Carmichael numbers are relatively few, which allows us to hope for a probabilistic test. Only when searching for primes, the hope of probability is excluded. That is why, after selecting candidates for simple ones with the help of probability tests, the Luc-Lemer test is nevertheless applied.
Add a little about Carmichael numbers. They are remarkable not only for their ability to imitate the simple. So, the network has a website where you can learn different sequences of numbers . If you enter the number 561 (the minimum Carmichael number) in the search field, you can find that it participates in a very large number of sequences. What is this talking about? Apparently about some yet unknown structural properties of similar numbers that are very common in our world. Very entertaining fact.
But back to the simplicity tests. Despite a good filtering coefficient with probabilistic tests, mankind spends years finding the next maximum prime number. Why? Because the dependence of the test execution time on the size of the number is quadratic. That is, for small numbers everything goes off with a bang and there are no problems, but when numbers increase a million times, the time for calculations increases a trillion times. Therefore, on one processor core, we would consider the Luc-Lemer test for decades. But even a farm formula test, we would also consider about the same. That is, in both approaches, the number of calculations has reached the limits of human capabilities. You have to do something with this, don’t you find it?
What can be the alternatives to such a wasteful computing waste on air heating for many years? Very simple - you need to predict simplicity by the nature of the number, by its membership in a particular class. So Mersenne numbers became leaders in the achieved sizes of proven primes precisely because of their belonging to a specific class. The Luke-Lemer test works specifically for such a specific class. The numbers of other classes are lagging behind due to the lack of even such an expensive test as the Luc-Lemer test for ten-megabyte numbers (although for some, this test is adapted). So we need a classification of numbers that allows us to find simple simplicity tests, so heaven forgive me for such a pun.
How to create such a classification? It’s also not so difficult - you need to explore different numbers and identify common features between them. In general, this is exactly what mathematicians are trying to do, but so far a stone flower has not come out. Therefore, we will try to help them.
The previously described approach for analyzing numbers based on residual tables essentially explores the divisibility of numbers of the form 1000 ... 000. That is, the zeros on the right are constantly assigned to the unit, thereby multiplying it by the basis of each of the number systems present in the remainder table. As a result of the analysis, we found that different numbers divide numbers of the form 1000 ... 000 in different ways. So prime numbers generally cannot divide one with zeros. But the components, and even, for example, of twos and / or fives, are completely divided. Below is a table for the number 8:

As you can see, in it, in lines that are multiples of 2, after some entry from nonzero residues, only one zeros remain. This is exactly what all numbers related to the class of divisors of units with zeros look like, and the presence of zeros tells us in which number systems we will succeed. But here's the problem - from the point of view of finding prime numbers, a unit with zeros is not at all interesting to us, because it is guaranteed to be divided by the base of the number system, which gives us all these zeros after one. So you need to explore the divisibility of other classes of numbers. Is it logical? This is exactly what we will do.
Earlier we got acquainted with the regularities of the remainder tables for the division operation, which is relatively familiar to us. The patterns turned out to be entertaining, but they still have the same problem - they do not give us a quick algorithm for checking simplicity. For such a test, we, as in the test according to the Fermat formula, will have to raise the numbers to a very large degree, and then find the remainder of dividing the result by the number under study. Or simply iterate over all the remains using the “corner” method (before the thermal death of the universe, of course). Here is the data - the operation of raising to a power with finding the remainder takes 15 minutes on one core for numbers of order . With an increase in the number size by 1000 times, we get a quadratic increase (plus logarithms, but this is not so much) at least 1,000,000 times, but in reality - many million times. Suppose, as a result, we get a million hours for one test. This is approximately 40,000 days or noticeably more than a hundred years. If we optimize the execution of the test to its very ears, perform it taking into account all the features of the processor architecture, then perhaps instead of a hundred years we get 10. On 10 cores - 1 year. For 1000 cores - 4 days. But this is just a probabilistic test, because there are masquerade as simple composite numbers. So you still need to double-check. But more important is the fact that the numbers of candidates are millions. After all the possible filtrations, there will also be a lot of them. Therefore, the world is still messing with ten megabyte numbers.
But we have a tool. The remainder table also works for other types of numbers. For example, take the Mersenne numbers. In binary, it's just a sequence of units. What prevents us from exploring a sequence of units instead of a sequence of zeros? Yes, nothing prevents. And it turns out that for such a sequence, our method works quite well and a number of previously identified patterns are preserved in it. Here is the result for the number 7:

As we can see, the prime number 7 in all number systems (except for multiples of seven) is a divisor of Mersenne numbers. That is, almost every line contains a zero that tells us about the divisibility of numbers of the form 111 ... 111 (in the binary system) by 7. So, when working with the binary number system, we see that the number 7 divides all the Mersenne numbers, the length which is a multiple of 3. This result is obvious even without a remainder table - the number 7 in binary form consists of three units (111), so it will divide the binary number of three units. And if there are more units, then the division looks like this:
That is, we simply put seven (in binary form) under the dividend. And how many times the seven will fit - so many triple units in a divisible number. If in it the number of units is not a multiple of three, then such a number is not divisible by 7. But this is all obvious only as long as we study numbers with an identical structure (7 and 63, as in the example). And if the structure of numbers is more complicated, a table of residuals will help us. So, for all simple we get a similar result, but with a slightly longer division period. Below is an example of the number 11 (the number is already in decimal):
We see that in the binary system the distance to zero (the divisibility period) for the number 11 is 10. That is, any Mersenne number containing 10k units, where k is an integer greater than zero, is necessarily divisible by 11. It can be easily proved that the rest are simple numbers behave exactly the same, except for the size of the period, of course. But for the compound, the situation is again less harmonious. Below we see an example for the number 8:

Apparently, 8 cannot divide Mersenne numbers in binary form. Here in the ternary - please, but the Mersenne numbers consist of units only in binary form. The situation is similar with other compound numbers - they have different things. A slender and symmetrical picture for primes does not repeat for compound ones. But for us it is precisely the simple ones that are important, because if the number is divided into a prime, then there is absolutely no problem if it will also be divided into a compound that includes this simple one. But if the number is not divided into a prime, then a division with such a simple division will be impossible. So we should be interested only in prime numbers.
Now let’s summarize. We know that Mersenne numbers are divided into primes and that for divisibility Mersenne numbers need a number of units that is a multiple of the period of divisibility of the number under study. But we also know that candidates for Mersenne primes are only those in which the number of units is also a prime. That is, this amount is not divided into anything but a unit and itself. Hence the conclusion - we need such a prime number whose divisibility period is equal to the length of the Mersenne number. If for some length of the Mersenne number we did not find a divisor with a suitable period, we have before us a prime Mersenne number. It seems simple.
But further difficulties begin. How to find a number whose period coincides with the length of the Mersenne number? To answer this question, you need to solve a modest task - to find a way by simple means to find out the period for an arbitrary prime number. For now, we can only share a corner or poke at some specific place using a formula with large degrees. But if we could calculate the period without the need for long calculations, then we would quickly find the right divisor, or we would make sure that there are none in nature. Exactly the same modest task awaits us in the case of studying the divisibility of numbers of the form 1000 ... 000. So the period of divisibility is very important in all respects.
Here, quantum computers rush to our aid. Once upon a time, in some time immemorial, a certain connoisseur of quantum physics by the name of Shor, suggested finding the period precisely with the help of a quantum computer. In fact, a quantum computer only gives an intermediate value, from which an ordinary computer then receives a period, but the point is not that, but that without a quantum computer, mathematics is not able to calculate the period. But calculating the period, we get the opportunity to accurately calculate the value of the remainder strictly in the middle of the period. Why is this needed? For the fact that from it you can get factors that necessarily contain a certain value that is a multiple of the divisor of the number under study. This is done by adding to the remainder of the unit and subtracting the unit. The resulting two numbers can be skipped through a fast algorithm for finding the largest common divisor with the number under study. In at least one case, this will give us the divisor of the number under investigation. True, not everything is so perfect, because as we saw in the example of the table for primes, in the middle of the series there is often an addition to the number being investigated (N-1), in this form we get:
From this it follows that in one case we have the studied number itself, and it makes no sense to calculate the greatest common factor, and in the second case, we have guaranteed that it does not have common divisors with the studied number. There are no common divisors because this number is only 2 less than the investigated number, which means that no matter what number fits into the studied integer number of times (would be its divisor), subtracting it from the studied number we get a guaranteed lower value than , or using the formulas:
Here N is an odd test number (odd because a multiple of two is divisible by two, and we need that no matter what is divisible), x is a divisor of N, k is the whole result of division , m is the whole division result . That is, we sometimes have to change the number system and ask the quantum computer to find a new period, in the hope that there will be a more suitable number in its middle. A plus limitation is the mandatory parity of the period length value. But this is not so scary, because in any case, a quantum computer will calculate the length (or several lengths) we need much faster than the thermal death of the universe occurs, unlike other algorithms.
Although calculating the period for obtaining number divisors is a slightly different task from finding simple ones. Nevertheless, we can add something here using the leftover tables. So the tables show that the middle of rows of even length is usually a number that satisfies the following condition:
Here r is the desired remainder, and N is the number under investigation. Thus, it turns out that there is no need to search for a period to obtain divisors of a number, because the period is searched to find the very remainder r, and then add and subtract one from it. That is, you can immediately find this remainder that satisfies the above condition. True, the search for such a value is also nontrivial. But can a quantum computer be imprisoned for such a thing? Experts in quantum computing need to understand how many qubits are needed for this (qubits are parrots that measure the "power" of a quantum computer). Although, perhaps, you can do without a quantum computer. To do this, you just need to understand what patterns will come in handy. Some of the patterns are visible in the tables of residuals, well, and the rest of the readers will have to figure out on their own, and then you will definitely crack RSA-based cryptography. True, there are a couple of difficulties - first you need to find these useful patterns, well, and then ... Then they may not pay you money. First, prizes give for large primes, not for hacking RSA. And secondly - well, think for yourself how many serious organizations in the world are interested in intercepting other people's data in this way? And then some FSB (the CIA, Mossad, Mi-5, just the Mafia) found out that you know something. Guess what will happen to you? Therefore, further you act solely at your own peril and risk.
True, the quantum topic itself is quite interesting in that it contains quantum uncertainty, vacuum fluctuations, and other quantum Darwinism. How can all this be explained? To be honest, I don’t know, but I see an analogy with the tables of residuals. For example, when someone observes the values in the residual table and does not know about the previously mentioned patterns, then for him there is only some noise in the table where the numbers change each other in some random way, like some fluctuations in the vacuum. But if you understand that we are just applying the same algorithm to different pairs of “sequence - number under investigation”, then all this boiling porridge from the numbers instantly becomes understandable. And in the same way, it becomes clear why among the huge number of possible values for filling the table, only strictly defined ones really remain in it. But until we get the “interaction” of the sequence with the number under study, we cannot predict the contents of the table. More precisely, any filling of it will be equally probable. But after the “interaction” - everything will become strictly logical, from the equally probable a single probability will be born for only one option. And not because a certain Darwinism works, but only because of the application of a certain algorithm to specific input data. If you don’t know about the algorithm, then it may seem that the rows in the table are really Darwin-style. And if you know - everything is very simple. Maybe in quantum physics it is necessary to search not only for particles, but also for an algorithm for their “division”?
Nevertheless, the period is very important for us. Yes, this is how they will answer you on the hot line on the burning problems of mathematics. As shown above, knowledge of the period makes it possible to understand whether a number has divisors, or in another way whether it is prime. Therefore, we continue about the period. So far, we know a number of period properties (uniqueness of values, symmetry with an even length, etc.), but we don’t know how to determine its length. Although there is an upper and lower boundary - the period cannot be longer than the number under investigation minus one, and also the period cannot be shorter than the growth period of the base of the number system until the number under study is exceeded (for seven it is 3, for 11 it is 4, etc. .). You can try to apply the laws known from the tables studied and derive new ones, but so far there are quite a few directions here, most of which do not lead to success, although until you try each, you won’t know.
Therefore, the most promising way is to create an improved theory of divisibility. Based on the characteristic sequences of residues, it is possible to reveal the laws of divisibility of many classes of numbers. So far, only two classes have been shown (Mersenne numbers and numbers equal to the powers of the number system), but in reality there are an infinite number of them. How to process knowledge on all classes of numbers? Only in massive parallel work, and not in the form of iron air heaters, but in the form of joint work of people on such a big task. The ideal result would be the creation of a general theory of divisibility of all classes of numbers. This is for starters, and then divisibility of polynomials and other algebra will go. But should we expect such a wonderful massing of human minds over the task of finding prime numbers? I suspect not. Therefore, sadly, we again need other ways.
If we study alternative divisible sequences, including differing values, it will be found that the period of division of such sequences grows a multiple of the length of the repeating fragments of the sequences. Below is an example of a divisible sequence of the form 1010 ... 1010, where zero and one change periodically. The given sequence is always divided into the base of the number system, but in this case, the simplicity of the example of studying the numbers of the periodic class is important only to us, so we don’t pay attention to the divisibility “by construction”.

Here we see two tables for the number 7 and the above sequence, one is normal, and the second table is multiplied by 3. From the previously identified patterns in this example, there is even less, but nevertheless, for number systems on bases 1 and 6, we see an increase period lengths to . And for multiplied by 3 tables, we see a loss of divisibility for the bases of number systems 2 and 5, which is quite entertaining in itself (the divisibility property has changed from multiplication). But more important than that. It is important to understand the possibility of applying divisibility tables to any sequences. But why do we need any sequences? For example, to increase the minimum period of divisibility.
If the minimum period can be lengthened, then this allows us to very simply proceed to the construction of primes. Yes, primes can not be calculated, but mathematically constructed. When a period is long, a small number divides a large one, which means that if all numbers have periods large, then for large numbers only small numbers can be divisors. What does it give? This makes it possible to find all the divisors of a large number by a simple enumeration. Since small numbers divide large numbers, the very size of these small numbers helps our computers solve the problem that they cannot solve with large divisors. Therefore, the further direction of the search for primes becomes clear - we need to find a sequence that gives us large minimum periods. Why the minimum? Because we still do not know how to calculate a period without enumerating all the residuals or raising to a power, and therefore we simply cannot find a sufficiently long period if it is greater than the minimum, well, the minimum is known to us simply from the analysis of the remainder tables, that is, we do not need to calculate it . Well, when we find the sequence we need (and just for this we need the analysis of many classes of such sequences), we simply select the length of the sequence that will not fit in any of the minimum periods known to us. That is, we will pick up such a large number, which obviously has no divisors. And if its size is large, a prize awaits us. At the same time, we will not be interested in periods greater than the minimum, because they already divide very large numbers, which we will reach sometime later.
All that’s left is to find the correct sequence. Who will take it? But even if we don’t find it, then for the encryption mentioned earlier, working with alternative sequences will make it possible to add another term to the cipher that increases cryptographic strength - now cipher crackers will need to guess the sequence we have chosen, which can be infinite in number. Plus, to generate pseudo-random sequences, we get the repeatability of the values in the series of residuals, and not just in the series of the fraction period.
Electronic Frontier Foundation is ready to pay anyone who wants it, first $ 150k, and then another $ 250k. In total - $ 400k . Wouldn't that bother you? Then to the point! But the thing is simple - you need to find a prime number of one hundred million decimal places. This is roughly 300 million bits, or 40 megabytes. Just left to overtake the current record 4 times. And then you need a billion decimal digits long. This is already 400 megabytes. And all, for two numbers - 400 thousand forever green dollars.
In fact, these are not such terrible figures. Now, if we could get away from calculating the remainder of dividing large degrees by the number under study ... For simple sequences of the form 100 ... 00 and 111 ... 111, the degree is necessarily present. But maybe there are sequences for which the formula for calculating the ith member of a series of residues will be simpler? Or you can really find a sequence with a large minimum period. After all, what period do we need? Only 300 million (in binary form). If a certain sequence gives us a minimum period of the form 100 * N, where N is the number under investigation, then up to 3 million numbers will be enough for us to find a worth 150k $ number. And up to 30 million for a $ 250k number. And now, when a short period can happen in a very large number (for sequences 100..00 and 111 ... 111), we do not have any simple possibilities for finding it. But there is hope and it all depends on the successful choice of the direction of the search. Iterating through the sequences one at a time is apparently not realistic for one person, but you can try the crowd.
Well, when you find the required numbers, a little bureaucracy awaits you. First you will have to publish an article in a mathematical journal in the USA or England or Canada or Australia, and the journal should be from the list indicated by the Electronic Frontier Foundation (EFF) (these are very reputable journals). In the article, you must prove that your method really makes it possible to find the desired prime number. Then you send a letter of happiness to the EFF (at a specific address), where you point to the published article and then await orders from the EFF. Orders may relate to checking everything you did to find the number. There should be no secrets, no illegal or dubious actions, either. And that's all, after that - your prize.
What ambushes can wait for you on the way? Well, for starters - to find a prime number and not make mistakes when searching for it. Next you need to write in a solid journal. Since the magazine is solid, the usual reaction of the editors to the letter of the next inventor of the perpetual motion machine is this:
- What? Another freak? In garbage!
But it is possible that you have experience in writing articles and you can easily cope with this problem. And then you will find a check. I don’t know what your evidence will be studied by EFF, but they write that they can be interested in everything, anything. It will be especially interesting if the EFF goals do not match the result you provide. So they declare the goal of developing methods for using personal computers for putting them into temporary remote use for third-party computing. The previous prize was given just for the creation and promotion of the program, which volunteers downloaded and thereby provided the necessary terraflops for grinding prime numbers.How EFF relates to calculating a prime without mass terraflops - I don’t know. Theoretically, there are no restrictions on their requirements, so success is entirely possible.
That's all, having gone through the two indicated stages (and not forgetting to find the necessary numbers at the zero stage), you indicate the bank and account number where the prize drops to you. One big sum. You deal with the tax at your own expense.
Once upon a time, Pierre Fermat, not being a mathematician, discovered many patterns for number theory. The man was just wondering, well, there was free time on hand. And here you have the achievements that are still remembered. Another example is Evarist Galois. He took up mathematics at the age of 16, and at the age of 20 he died in a duel. For 4 years he tried to interest many mathematicians with his finds, but did not succeed. After the death, his work was nevertheless appreciated and it is to them that we owe the creation of such a branch of mathematics as group theory, as well as the development of algebra. Again - it was interesting for a person to find the stars, but arranging the works according to the rules was not for him. But fortunately, his work was formalized by others. And another example - George Cantor, reflecting on the well-known concepts of the set and its element, one deduced the theory at the end of the 19th century,which outstanding mathematicians agreed to consider worthy to become the basis of the queen of sciences.
Why all these stories? As Mr. Obama used to say, “You can!” Yes, this American slogan is quite suitable for enthusiastic people. Despite the development of science today, it is not complete, it is not perfect, and there are places in it where the foot of a real scientist has not stepped. So let's turn on our curiosity and try to look for such untrammeled paths, and what if you succeed?
Search for simple
Having talked about the properties of the table of residuals, we can try to apply knowledge about it to earning. So many in the world find it useful to search for large primes. And even there are organizations that are ready to give a lot of money to someone who finds a large prime number. But the topic of quantum computing is also popular in the world. Why? Because it promises to hack a well-known cryptosystem. This, so to speak, is the advertising slogan of quantum computing, which allows convincing any decision-making manager to allocate money for such an interesting lesson. Therefore, we will talk about this topic.
First we’ll show you how to look for prime numbers. The main problem here is quantity. For large numbers, there are simply no algorithms that allow you to quickly check whether a prime number is in front of us or a compound one. Therefore, the maximum downtime for today is less than 25 million decimal places in length. This is only 10 megabytes, on such arrays modern processors show millisecond processing times, but to check whether a prime number is in our array, a modern processor will consume electricity and buzz with a fan for decades. That is, technically, the size for the processor is small, but the number of operations in known algorithms for such large numbers is simply huge. Why is this situation?
For simplicity tests, for example, enumeration of dividers is used. But how many divisors do you need to iterate over for a number ten megabytes long? The answer is that even atoms with electrons in the entire universe will be enough only for a tiny part of this value. That is, we need huge numbers of universes, just to place all these divisors there. Too much? Therefore, enumeration of divisors for ten-megabyte numbers is applied to a limited extent (yes, the universe let us down ...), but fortunately there are other algorithms. We can distinguish algorithms that do not use enumeration of divisors, and at the same time they are guaranteed to give an answer - simple in front of us or composite. But these are very slow algorithms. That is, they, of course, are capable of grinding numbers a hundred or two hundred bits that way, but ten megabytes for them is death all at once. Therefore, you have to get out the tricky ways.
But the problem with all the tricks is that they have not yet come up with a complete theory of divisibility. After all, if it were complete, we would very quickly find the answer - a prime or not. More precisely, a theory would quickly give us an algorithm for testing that would not keep us waiting until the thermal death of the universe. That's why they give bonuses to those who come up with an algorithm as quickly as possible, and, best of all, a whole theory to provide algorithms for all occasions.
In the meantime, we have at our disposal a specific Luc-Lemer test, which uses the connection of very specific Mersenne numbers with a certain sequence, but not the remainder of the division, as we recently observed, but the sums of the degrees of some irrational numbers. That is, the simplicity test was performed from the side, let's say, not quite obvious, although some here can pick up more complicated comparisons. But why were the degrees of irrational numbers closer to simplicity tests than all other advances in number theory? Apparently because mathematics does not know simple solutions. And as a result, a method was used, although not an obvious but still working, from the region not closest to integer calculations, approximately how the transition from Cartesian to polar coordinates helps to use additional methods that are very difficult to implement in Cartesian coordinates.
In addition to the Luke-Lemer test, there are also probabilistic tests. They help weed out guaranteed compound numbers. So one of the actively used probabilistic tests is a test based on the Fermat formula, which we recently spoke about. How does he work? Very simple - remember the column of units on the right in the remainder table? This is a guaranteed sign of the simplicity of a number. To explain the verification using Fermat’s formula, mathematicians use specific terminology that few people understand except for them, so we won’t go into these mathematical jungles, but explain everything on the fingers, or rather, from the table of residuals. To understand what the remainder will be in the last column, you need to either divide by a column and reach the remainder at the position containing 1 in it, or calculate this remainder using the formula that allows you to get the remainder by the position number and the base of the number system. The first option for numbers ten megabytes long will require almost infinite time, because the width of the table is N-1, which means that for a number of the order of a million, the table will have a minimum of a million columns. For a billion, a billion. For a trillion, a trillion. But a trillion, it's only 12 decimal places. And we are interested in a number in which under 25 million characters. Even a trillion residues by the method of dividing the column we have to calculate hardly less than half an hour, and this is only 12 decimal places. Total! Compared to 25 million. Do you think you have enough time to wait for the result in this way? That is why it is better to immediately calculate the desired value using the formula. And just the Fermat formula corresponds to the formula for calculating the remainder in the last position in the table. Moreover, if the period is shorter than the width of the table, then mathematics does not yet know how to calculate it, which means that in any case, we need to choose the last column. The mathematicians in the test simply check whether the remainder in the last column is equal to one for the number system they have chosen (although mathematicians do not use the concept of the number system, for them there is only a basis raised to a power). If the remainder is not equal to one, the number is guaranteed to be composite. As we saw in the example of the table for the number 21, it is the absence of a unit at the end of many lines that distinguishes it from the tables for primes. But there is one problem. There may still be units in some lines, which we could also verify just by the example of the table for 21. That is why mathematicians call the test based on the Fermat formula probabilistic. That is, they do not know if the number is prime if the Fermat test found a remainder equal to one, because such false units are in the table for the number 21, and in many other tables, even for ten megabyte numbers. So you need to either check all the lines in a row, which is a very long time, because the lines for a ten-megabyte number, as noted earlier, are much more than everything in the universe we know, or just say - it is likely that this number is prime. Here is the last method and mathematicians have chosen. Fortunately, there are few lines ending with a unit in most composite numbers. True, there are also the so-called Carmichael numbers, in which all lines, except multiples of the divisors of such a number, end by one. So, on the Carmichael numbers, the probabilistic test by the Fermat formula is practically guaranteed to be wrong, because to eliminate the error you need to get into a multiple of the number divisor, and there can be only two divisors in the ten-megabyte number, and their value can be very large, and therefore the probability of getting exactly in such a line with a random choice of the base of the number system is practically zero. But on the other hand, Carmichael numbers are relatively few, which allows us to hope for a probabilistic test. Only when searching for primes, the hope of probability is excluded. That is why, after selecting candidates for simple ones with the help of probability tests, the Luc-Lemer test is nevertheless applied.
Add a little about Carmichael numbers. They are remarkable not only for their ability to imitate the simple. So, the network has a website where you can learn different sequences of numbers . If you enter the number 561 (the minimum Carmichael number) in the search field, you can find that it participates in a very large number of sequences. What is this talking about? Apparently about some yet unknown structural properties of similar numbers that are very common in our world. Very entertaining fact.
But back to the simplicity tests. Despite a good filtering coefficient with probabilistic tests, mankind spends years finding the next maximum prime number. Why? Because the dependence of the test execution time on the size of the number is quadratic. That is, for small numbers everything goes off with a bang and there are no problems, but when numbers increase a million times, the time for calculations increases a trillion times. Therefore, on one processor core, we would consider the Luc-Lemer test for decades. But even a farm formula test, we would also consider about the same. That is, in both approaches, the number of calculations has reached the limits of human capabilities. You have to do something with this, don’t you find it?
What can be the alternatives to such a wasteful computing waste on air heating for many years? Very simple - you need to predict simplicity by the nature of the number, by its membership in a particular class. So Mersenne numbers became leaders in the achieved sizes of proven primes precisely because of their belonging to a specific class. The Luke-Lemer test works specifically for such a specific class. The numbers of other classes are lagging behind due to the lack of even such an expensive test as the Luc-Lemer test for ten-megabyte numbers (although for some, this test is adapted). So we need a classification of numbers that allows us to find simple simplicity tests, so heaven forgive me for such a pun.
How to create such a classification? It’s also not so difficult - you need to explore different numbers and identify common features between them. In general, this is exactly what mathematicians are trying to do, but so far a stone flower has not come out. Therefore, we will try to help them.
The previously described approach for analyzing numbers based on residual tables essentially explores the divisibility of numbers of the form 1000 ... 000. That is, the zeros on the right are constantly assigned to the unit, thereby multiplying it by the basis of each of the number systems present in the remainder table. As a result of the analysis, we found that different numbers divide numbers of the form 1000 ... 000 in different ways. So prime numbers generally cannot divide one with zeros. But the components, and even, for example, of twos and / or fives, are completely divided. Below is a table for the number 8:

As you can see, in it, in lines that are multiples of 2, after some entry from nonzero residues, only one zeros remain. This is exactly what all numbers related to the class of divisors of units with zeros look like, and the presence of zeros tells us in which number systems we will succeed. But here's the problem - from the point of view of finding prime numbers, a unit with zeros is not at all interesting to us, because it is guaranteed to be divided by the base of the number system, which gives us all these zeros after one. So you need to explore the divisibility of other classes of numbers. Is it logical? This is exactly what we will do.
Can we try the theory of divisibility?
Earlier we got acquainted with the regularities of the remainder tables for the division operation, which is relatively familiar to us. The patterns turned out to be entertaining, but they still have the same problem - they do not give us a quick algorithm for checking simplicity. For such a test, we, as in the test according to the Fermat formula, will have to raise the numbers to a very large degree, and then find the remainder of dividing the result by the number under study. Or simply iterate over all the remains using the “corner” method (before the thermal death of the universe, of course). Here is the data - the operation of raising to a power with finding the remainder takes 15 minutes on one core for numbers of order . With an increase in the number size by 1000 times, we get a quadratic increase (plus logarithms, but this is not so much) at least 1,000,000 times, but in reality - many million times. Suppose, as a result, we get a million hours for one test. This is approximately 40,000 days or noticeably more than a hundred years. If we optimize the execution of the test to its very ears, perform it taking into account all the features of the processor architecture, then perhaps instead of a hundred years we get 10. On 10 cores - 1 year. For 1000 cores - 4 days. But this is just a probabilistic test, because there are masquerade as simple composite numbers. So you still need to double-check. But more important is the fact that the numbers of candidates are millions. After all the possible filtrations, there will also be a lot of them. Therefore, the world is still messing with ten megabyte numbers.
But we have a tool. The remainder table also works for other types of numbers. For example, take the Mersenne numbers. In binary, it's just a sequence of units. What prevents us from exploring a sequence of units instead of a sequence of zeros? Yes, nothing prevents. And it turns out that for such a sequence, our method works quite well and a number of previously identified patterns are preserved in it. Here is the result for the number 7:

As we can see, the prime number 7 in all number systems (except for multiples of seven) is a divisor of Mersenne numbers. That is, almost every line contains a zero that tells us about the divisibility of numbers of the form 111 ... 111 (in the binary system) by 7. So, when working with the binary number system, we see that the number 7 divides all the Mersenne numbers, the length which is a multiple of 3. This result is obvious even without a remainder table - the number 7 in binary form consists of three units (111), so it will divide the binary number of three units. And if there are more units, then the division looks like this:
111111 | 111 ------ 111 1001 111 111 111
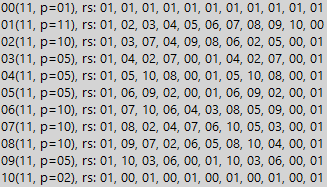
That is, we simply put seven (in binary form) under the dividend. And how many times the seven will fit - so many triple units in a divisible number. If in it the number of units is not a multiple of three, then such a number is not divisible by 7. But this is all obvious only as long as we study numbers with an identical structure (7 and 63, as in the example). And if the structure of numbers is more complicated, a table of residuals will help us. So, for all simple we get a similar result, but with a slightly longer division period. Below is an example of the number 11 (the number is already in decimal):

We see that in the binary system the distance to zero (the divisibility period) for the number 11 is 10. That is, any Mersenne number containing 10k units, where k is an integer greater than zero, is necessarily divisible by 11. It can be easily proved that the rest are simple numbers behave exactly the same, except for the size of the period, of course. But for the compound, the situation is again less harmonious. Below we see an example for the number 8:

Apparently, 8 cannot divide Mersenne numbers in binary form. Here in the ternary - please, but the Mersenne numbers consist of units only in binary form. The situation is similar with other compound numbers - they have different things. A slender and symmetrical picture for primes does not repeat for compound ones. But for us it is precisely the simple ones that are important, because if the number is divided into a prime, then there is absolutely no problem if it will also be divided into a compound that includes this simple one. But if the number is not divided into a prime, then a division with such a simple division will be impossible. So we should be interested only in prime numbers.
Now let’s summarize. We know that Mersenne numbers are divided into primes and that for divisibility Mersenne numbers need a number of units that is a multiple of the period of divisibility of the number under study. But we also know that candidates for Mersenne primes are only those in which the number of units is also a prime. That is, this amount is not divided into anything but a unit and itself. Hence the conclusion - we need such a prime number whose divisibility period is equal to the length of the Mersenne number. If for some length of the Mersenne number we did not find a divisor with a suitable period, we have before us a prime Mersenne number. It seems simple.
But further difficulties begin. How to find a number whose period coincides with the length of the Mersenne number? To answer this question, you need to solve a modest task - to find a way by simple means to find out the period for an arbitrary prime number. For now, we can only share a corner or poke at some specific place using a formula with large degrees. But if we could calculate the period without the need for long calculations, then we would quickly find the right divisor, or we would make sure that there are none in nature. Exactly the same modest task awaits us in the case of studying the divisibility of numbers of the form 1000 ... 000. So the period of divisibility is very important in all respects.
How to find a period?
Here, quantum computers rush to our aid. Once upon a time, in some time immemorial, a certain connoisseur of quantum physics by the name of Shor, suggested finding the period precisely with the help of a quantum computer. In fact, a quantum computer only gives an intermediate value, from which an ordinary computer then receives a period, but the point is not that, but that without a quantum computer, mathematics is not able to calculate the period. But calculating the period, we get the opportunity to accurately calculate the value of the remainder strictly in the middle of the period. Why is this needed? For the fact that from it you can get factors that necessarily contain a certain value that is a multiple of the divisor of the number under study. This is done by adding to the remainder of the unit and subtracting the unit. The resulting two numbers can be skipped through a fast algorithm for finding the largest common divisor with the number under study. In at least one case, this will give us the divisor of the number under investigation. True, not everything is so perfect, because as we saw in the example of the table for primes, in the middle of the series there is often an addition to the number being investigated (N-1), in this form we get:
From this it follows that in one case we have the studied number itself, and it makes no sense to calculate the greatest common factor, and in the second case, we have guaranteed that it does not have common divisors with the studied number. There are no common divisors because this number is only 2 less than the investigated number, which means that no matter what number fits into the studied integer number of times (would be its divisor), subtracting it from the studied number we get a guaranteed lower value than , or using the formulas:
N-x <N-2 \ Rightarrow x> 2 \; \ & \; (N-2) / x \ ne m
Here N is an odd test number (odd because a multiple of two is divisible by two, and we need that no matter what is divisible), x is a divisor of N, k is the whole result of division , m is the whole division result . That is, we sometimes have to change the number system and ask the quantum computer to find a new period, in the hope that there will be a more suitable number in its middle. A plus limitation is the mandatory parity of the period length value. But this is not so scary, because in any case, a quantum computer will calculate the length (or several lengths) we need much faster than the thermal death of the universe occurs, unlike other algorithms.
Although calculating the period for obtaining number divisors is a slightly different task from finding simple ones. Nevertheless, we can add something here using the leftover tables. So the tables show that the middle of rows of even length is usually a number that satisfies the following condition:
Here r is the desired remainder, and N is the number under investigation. Thus, it turns out that there is no need to search for a period to obtain divisors of a number, because the period is searched to find the very remainder r, and then add and subtract one from it. That is, you can immediately find this remainder that satisfies the above condition. True, the search for such a value is also nontrivial. But can a quantum computer be imprisoned for such a thing? Experts in quantum computing need to understand how many qubits are needed for this (qubits are parrots that measure the "power" of a quantum computer). Although, perhaps, you can do without a quantum computer. To do this, you just need to understand what patterns will come in handy. Some of the patterns are visible in the tables of residuals, well, and the rest of the readers will have to figure out on their own, and then you will definitely crack RSA-based cryptography. True, there are a couple of difficulties - first you need to find these useful patterns, well, and then ... Then they may not pay you money. First, prizes give for large primes, not for hacking RSA. And secondly - well, think for yourself how many serious organizations in the world are interested in intercepting other people's data in this way? And then some FSB (the CIA, Mossad, Mi-5, just the Mafia) found out that you know something. Guess what will happen to you? Therefore, further you act solely at your own peril and risk.
True, the quantum topic itself is quite interesting in that it contains quantum uncertainty, vacuum fluctuations, and other quantum Darwinism. How can all this be explained? To be honest, I don’t know, but I see an analogy with the tables of residuals. For example, when someone observes the values in the residual table and does not know about the previously mentioned patterns, then for him there is only some noise in the table where the numbers change each other in some random way, like some fluctuations in the vacuum. But if you understand that we are just applying the same algorithm to different pairs of “sequence - number under investigation”, then all this boiling porridge from the numbers instantly becomes understandable. And in the same way, it becomes clear why among the huge number of possible values for filling the table, only strictly defined ones really remain in it. But until we get the “interaction” of the sequence with the number under study, we cannot predict the contents of the table. More precisely, any filling of it will be equally probable. But after the “interaction” - everything will become strictly logical, from the equally probable a single probability will be born for only one option. And not because a certain Darwinism works, but only because of the application of a certain algorithm to specific input data. If you don’t know about the algorithm, then it may seem that the rows in the table are really Darwin-style. And if you know - everything is very simple. Maybe in quantum physics it is necessary to search not only for particles, but also for an algorithm for their “division”?
And again about the period
Nevertheless, the period is very important for us. Yes, this is how they will answer you on the hot line on the burning problems of mathematics. As shown above, knowledge of the period makes it possible to understand whether a number has divisors, or in another way whether it is prime. Therefore, we continue about the period. So far, we know a number of period properties (uniqueness of values, symmetry with an even length, etc.), but we don’t know how to determine its length. Although there is an upper and lower boundary - the period cannot be longer than the number under investigation minus one, and also the period cannot be shorter than the growth period of the base of the number system until the number under study is exceeded (for seven it is 3, for 11 it is 4, etc. .). You can try to apply the laws known from the tables studied and derive new ones, but so far there are quite a few directions here, most of which do not lead to success, although until you try each, you won’t know.
Therefore, the most promising way is to create an improved theory of divisibility. Based on the characteristic sequences of residues, it is possible to reveal the laws of divisibility of many classes of numbers. So far, only two classes have been shown (Mersenne numbers and numbers equal to the powers of the number system), but in reality there are an infinite number of them. How to process knowledge on all classes of numbers? Only in massive parallel work, and not in the form of iron air heaters, but in the form of joint work of people on such a big task. The ideal result would be the creation of a general theory of divisibility of all classes of numbers. This is for starters, and then divisibility of polynomials and other algebra will go. But should we expect such a wonderful massing of human minds over the task of finding prime numbers? I suspect not. Therefore, sadly, we again need other ways.
Theoretically, there is such a way
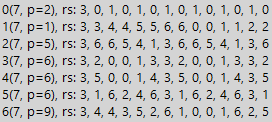
If we study alternative divisible sequences, including differing values, it will be found that the period of division of such sequences grows a multiple of the length of the repeating fragments of the sequences. Below is an example of a divisible sequence of the form 1010 ... 1010, where zero and one change periodically. The given sequence is always divided into the base of the number system, but in this case, the simplicity of the example of studying the numbers of the periodic class is important only to us, so we don’t pay attention to the divisibility “by construction”.


Here we see two tables for the number 7 and the above sequence, one is normal, and the second table is multiplied by 3. From the previously identified patterns in this example, there is even less, but nevertheless, for number systems on bases 1 and 6, we see an increase period lengths to . And for multiplied by 3 tables, we see a loss of divisibility for the bases of number systems 2 and 5, which is quite entertaining in itself (the divisibility property has changed from multiplication). But more important than that. It is important to understand the possibility of applying divisibility tables to any sequences. But why do we need any sequences? For example, to increase the minimum period of divisibility.
If the minimum period can be lengthened, then this allows us to very simply proceed to the construction of primes. Yes, primes can not be calculated, but mathematically constructed. When a period is long, a small number divides a large one, which means that if all numbers have periods large, then for large numbers only small numbers can be divisors. What does it give? This makes it possible to find all the divisors of a large number by a simple enumeration. Since small numbers divide large numbers, the very size of these small numbers helps our computers solve the problem that they cannot solve with large divisors. Therefore, the further direction of the search for primes becomes clear - we need to find a sequence that gives us large minimum periods. Why the minimum? Because we still do not know how to calculate a period without enumerating all the residuals or raising to a power, and therefore we simply cannot find a sufficiently long period if it is greater than the minimum, well, the minimum is known to us simply from the analysis of the remainder tables, that is, we do not need to calculate it . Well, when we find the sequence we need (and just for this we need the analysis of many classes of such sequences), we simply select the length of the sequence that will not fit in any of the minimum periods known to us. That is, we will pick up such a large number, which obviously has no divisors. And if its size is large, a prize awaits us. At the same time, we will not be interested in periods greater than the minimum, because they already divide very large numbers, which we will reach sometime later.
All that’s left is to find the correct sequence. Who will take it? But even if we don’t find it, then for the encryption mentioned earlier, working with alternative sequences will make it possible to add another term to the cipher that increases cryptographic strength - now cipher crackers will need to guess the sequence we have chosen, which can be infinite in number. Plus, to generate pseudo-random sequences, we get the repeatability of the values in the series of residuals, and not just in the series of the fraction period.
And finally - the prizes!
Electronic Frontier Foundation is ready to pay anyone who wants it, first $ 150k, and then another $ 250k. In total - $ 400k . Wouldn't that bother you? Then to the point! But the thing is simple - you need to find a prime number of one hundred million decimal places. This is roughly 300 million bits, or 40 megabytes. Just left to overtake the current record 4 times. And then you need a billion decimal digits long. This is already 400 megabytes. And all, for two numbers - 400 thousand forever green dollars.
In fact, these are not such terrible figures. Now, if we could get away from calculating the remainder of dividing large degrees by the number under study ... For simple sequences of the form 100 ... 00 and 111 ... 111, the degree is necessarily present. But maybe there are sequences for which the formula for calculating the ith member of a series of residues will be simpler? Or you can really find a sequence with a large minimum period. After all, what period do we need? Only 300 million (in binary form). If a certain sequence gives us a minimum period of the form 100 * N, where N is the number under investigation, then up to 3 million numbers will be enough for us to find a worth 150k $ number. And up to 30 million for a $ 250k number. And now, when a short period can happen in a very large number (for sequences 100..00 and 111 ... 111), we do not have any simple possibilities for finding it. But there is hope and it all depends on the successful choice of the direction of the search. Iterating through the sequences one at a time is apparently not realistic for one person, but you can try the crowd.
Well, when you find the required numbers, a little bureaucracy awaits you. First you will have to publish an article in a mathematical journal in the USA or England or Canada or Australia, and the journal should be from the list indicated by the Electronic Frontier Foundation (EFF) (these are very reputable journals). In the article, you must prove that your method really makes it possible to find the desired prime number. Then you send a letter of happiness to the EFF (at a specific address), where you point to the published article and then await orders from the EFF. Orders may relate to checking everything you did to find the number. There should be no secrets, no illegal or dubious actions, either. And that's all, after that - your prize.
What ambushes can wait for you on the way? Well, for starters - to find a prime number and not make mistakes when searching for it. Next you need to write in a solid journal. Since the magazine is solid, the usual reaction of the editors to the letter of the next inventor of the perpetual motion machine is this:
- What? Another freak? In garbage!
But it is possible that you have experience in writing articles and you can easily cope with this problem. And then you will find a check. I don’t know what your evidence will be studied by EFF, but they write that they can be interested in everything, anything. It will be especially interesting if the EFF goals do not match the result you provide. So they declare the goal of developing methods for using personal computers for putting them into temporary remote use for third-party computing. The previous prize was given just for the creation and promotion of the program, which volunteers downloaded and thereby provided the necessary terraflops for grinding prime numbers.How EFF relates to calculating a prime without mass terraflops - I don’t know. Theoretically, there are no restrictions on their requirements, so success is entirely possible.
That's all, having gone through the two indicated stages (and not forgetting to find the necessary numbers at the zero stage), you indicate the bank and account number where the prize drops to you. One big sum. You deal with the tax at your own expense.
Instead of an epilogue
Once upon a time, Pierre Fermat, not being a mathematician, discovered many patterns for number theory. The man was just wondering, well, there was free time on hand. And here you have the achievements that are still remembered. Another example is Evarist Galois. He took up mathematics at the age of 16, and at the age of 20 he died in a duel. For 4 years he tried to interest many mathematicians with his finds, but did not succeed. After the death, his work was nevertheless appreciated and it is to them that we owe the creation of such a branch of mathematics as group theory, as well as the development of algebra. Again - it was interesting for a person to find the stars, but arranging the works according to the rules was not for him. But fortunately, his work was formalized by others. And another example - George Cantor, reflecting on the well-known concepts of the set and its element, one deduced the theory at the end of the 19th century,which outstanding mathematicians agreed to consider worthy to become the basis of the queen of sciences.
Why all these stories? As Mr. Obama used to say, “You can!” Yes, this American slogan is quite suitable for enthusiastic people. Despite the development of science today, it is not complete, it is not perfect, and there are places in it where the foot of a real scientist has not stepped. So let's turn on our curiosity and try to look for such untrammeled paths, and what if you succeed?
All Articles