Just division, or how to create a mathematical theory and earn $ 400K on it
It so happened that science is developing unevenly, and therefore in our life today, so to speak, there is a place for achievement. The feat, of course, is scientific, but from this no less significant. And now, readers, you are given the opportunity to see the place of the feat, the official prices for its payment (as is customary in countries that call themselves civilized), and even try your luck yourself. Well, at the same time, at least some of you will feel the charm of finding pearls in quite ordinary things.
Further, in several series, a story will be followed about things that are accessible to any high school graduate (and even many schoolchildren). There will be no evidence, since they are often obvious, and if presented here would not only stretch the volume, but would also scare away many readers.

First there were stars. There was a process of playing with them, looking at and feeling, tossing up and observing a shining fall path. The stars were patterns. And the sandbox was numbers. The numbers turned on a new side, and another star appeared in the gaps between them. Her radiance attracted and, best of all, did not burn, but allowed herself to be touched, picked up, and then waved to them in order to leave a sparkling trace of stardust. But then the stars became familiar and there was only one job left to sort them. And then an idea came up.
The idea was simple - you can make money on it. And yes, it really motivated. But it did not grow together. It was entertaining, there were regular stars shining in a new way, there was pleasure and there was progress. Only in the end did a forest arise, a continuous forest of shining trees. And I was weak, I could not sort this taiga in search of true light, because there are millions of trees, and I am alone. Therefore, I suggest you look at the stars, and if they are interesting, then you can earn $ 400K, but the truth is there is one “but” - in the forest you need to be able to choose the right path.
What is a number? On the one hand, it is a product of our gloomy mind, not found in nature. But on the other hand, such an abstraction allows us to simulate many processes that we observe all in the same nature. Only the model is not equal to the observed phenomenon. So again we are dealing with adaptation to our modest capabilities of the ways of describing nature. Is it good? In terms of accuracy, the description is not very good. Not because someone may not have enough decimal places, but because an inaccurately modeled phenomenon can surprise us a lot when it turns out that the model lacks one specific feature or another, which is present in reality and can sometimes make a little noise inattentive naturalists on the head.
In light of the foregoing, let us try to inquire about the completeness of the basis of any modeling - the completeness of understanding the concept of number. Just a number, just knowledge about it, laid down from early childhood, it seems - well, what else could it be? But just there we can find the abyss. Yes, the one that is without a bottom, and which is full of stars.
There are no numbers in nature. But in nature you can see the relationship. The cloud is larger (longer / wider / thicker / like_you_ else_will_be_becoming) another cloud, which means there is a place for correlation. But the ratio also has no numbers. There are only two clouds, one more, the other less, and there is their ratio. Although yes, the ratio was also invented by man. Therefore, one may ask - what is the use of it? The benefit is this - the concept of correlation is one step ahead of the concept of number. At first there was a ratio, and only then did a number appear. More precisely - fractional numbers. Therefore, understanding the relationship, we will understand the numbers.
How are fractional numbers obtained? Very simple - from the need to model correlation. At first there were ratios of steps and sides of land, sheep from one owner to sheep from another, the weight of one watermelon to the weight of another. In all these cases, there was a need to somehow express the difference. But the difference was not divided strictly by the number of steps or the size of the neighboring watermelon. At first they learned to express the difference by dividing them into smaller units of measure (elbows were added to the steps, and fingers were added to the elbows). But science did not stand still and demanded ever greater accuracy. As a result, everyone agreed on uniformity, forgetting about fingers, elbows, steps and other pounds with sterling. Uniformity is expressed in number.
How to correlate two segments if one of them does not fit into the other an integer number of times? You can measure with your fingers, but it will be more accurate to take a smaller segment as a unit of measurement and divide it into identical parts. With these parts, you can measure that part of a larger segment that is not measured by the entire smaller segment. But then a new part of the larger segment arises, which is no longer measurable by the selected parts. We apply recursion and again break the already broken parts into even smaller components. We measure them previously immeasurable. And again we get an immeasurable remainder. Divide the parts again, measure again. Again we get the remainder. But you can get bored!
As a result, people came up with the idea of rounding and stopped re-dividing the unit of measurement. That is, people scored on accuracy (they say it is sufficient). But nature does not forgive inaccuracies in modeling.
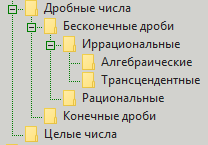
How are ratios modeled today? They are modeled using the classification of fractional numbers. The classification is this - there are integers and there are fractional numbers. Whole ones are unstable, but fractional ones are divided into finite and infinite fractions. For the time being, we also forget about the final ones. Infinite are divided into rational and irrational. We usually forget about the first part. The irrational are divided into algebraic and transcendental. Everything, no more divisions. But for clarity, we give a classification in the form of a picture:
Why is this classification bad? She's not that bad. She, as Winnie the Pooh used to say, is good, but somehow lame ... That is, it is clear that with the accuracy of the expression of values, she is not all right because of infinity. But there is another side to the coin. This side (in this context) is called "divisibility". We cannot precisely separate two numbers (one on another) because we rest against infinity. But then we are interested in such phenomena from the world of numbers as simplicity and the number of divisors that eliminate infinity when they appear. Prime numbers form the basis of the number series of integers. And these important numbers (including, for example, for comfort when remotely paying for services) numbers are very dependent on the division operation. And division often gives us fractions. And fractions give us fractional numbers. Well, for fractional numbers, someone gave us the previously given classification of finite, infinite, rational, irrational, algebraic and transcendental. But does this classification give us the opportunity to find answers to questions about numbers? For example, about the same simple ones? Or about fractional? It seems to give, but not as much as we would like.
Take prime numbers. Today, the maximum prime numbers are searched in essence by exhaustive search. That is, they take the candidate number, and then check whether it is simple or not. Candidates get numbers simply - if you know the method of checking simplicity for a certain class of numbers, then here is the list of candidates in the form of representatives of the class that they go through stupidly in a row, checking each number, starting, of course, with small values. And so far they have come to numbers of the order of two to the degree of eighty-odd million. This is a number of almost twenty-five million decimal places. In principle, it looks impressive. But what prevents us from recalling the slogan “higher, further, faster”?
Fundamentally, we are hindered by a lack of understanding. Yes, our model of the phenomenon called “number” is incomplete. And yes, the part of the model called “division” is most incomplete. Therefore, eighty million units in computer memory is the limit for humanity. Why units? Because it looks like the biggest prime numbers. These are one units, but in binary notation. For them, there is the Luc-Lemer test, which shows us a simple number or a compound. And this test requires years of work of one processor core to check one candidate number of eighty million binary units. Only eighty megabytes, or ten megabytes, and humanity is no longer able to step further. What is ten megabytes? This is a penny, this is a trifle, it is almost nothing for modern computers. But the test has been going on for years. Therefore, you have to run it on millions of computers on which volunteers install the appropriate program, and as a result check one candidate number for a certain number of seconds (and this if there are a lot of volunteers). But the problem is that there are a lot of candidate numbers, and therefore it takes many months to find the next prime number. And with such deliberation, one can expect that the movement of only up to hundreds of millions of binary units will take ten years.
Is it possible to speed up the process? Can. But more understanding is needed. For example - how to reduce the time to test each number? So far, such a decrease is achieved by massaging iron. Or the second option - you can offer a quicker test of simplicity. But with this for about 100 years, little has changed. And yet, if you figure it out, then maybe it will work out with us. Only need to understand from the very basics.
Thinking about the relationships, everyone can contribute a lot to science. Just being curious is enough. For example, one may ask, why is the classification of fractional numbers just this? And find the answer in a thought experiment to measure the ratio of the same segments. First, the segments are correlated as 1 to 2. This ratio is understandable, it gives us the number 2, which shows how many times the larger segment exceeds the smaller. And now let’s lengthen a slightly smaller segment. What will happen? The ratio will cease to be whole. The excess obtained from lengthening prevents us from obtaining a simple answer in the problem. But we can use it as a ruler. If it fits an integer number of times in half a larger segment, then we can express the ratio through this integer. So we get the ratio:
where N is the number of times it takes to fit the excess from stretching the smaller length into half the larger length. So we got a rational number. It is always given by the ratio of integers. If we now lengthen the smaller segment a little more, then we can get a situation where no matter how much we multiply the smaller segment by a certain integer, we cannot get an exact match with a certain number of lengths of the larger segment. So we got an irrational number that characterizes the new ratio. Note that a microscopic shift of the segment boundary leads to an endless process of identifying the ratio of lengths. One step for the humble researcher and a huge change for number theory - a new element in the classification is required. One step and - from micro-size right to infinity. From one category of numbers to a completely new one, fundamentally incompatible with the previous one. Isn't that a star?
But in fact, we just slightly changed one segment. So where did the fundamentally new category come from? In general, classification is important for its ability to exactly match reality. But what kind of accuracy came along with irrational numbers? They allow you to model any ratio, and not just the ratio of integers, so it really makes sense to separate such classes. But this is not all accuracy, because I want to understand all these infinities, how they appear, what they mean and why they exist at all. True, with infinities, everything is not easy, but because for now we will deal with finite relationships. It seems that everything is simple with them, take N, divide it by M, and get a fractional number. It will be very good if the number turns out to be short, for example 2.5 or 3.25. But more often to the world are relations of the form 4.12 (3456), that is, again with infinities, but these are infinities “in period”. Just by noticing repeating numbers, you can write down a number from an infinite number of characters very simply and compactly. That's how we famously coped with infinity. Also a small asterisk. But this is only a cursory glance.
Now let's turn on curiosity and ask questions. And why are some fractional numbers finite and others infinite? And why are some types of infinite infinitely long, while others with a period? And why before the period in number 4.12 (3456) we see the numbers 1 and 2? And why does there exist a preperiod? And why in the period do we see numbers 3 and 4? And why is the period length in this example equal to four? And why is the number of numbers before the period equal to two? And we only superficially cast a curious look at just one fractional number. And for other numbers, the questions will be even more interesting.
Let's try to answer. Why are fractional numbers finite? Very simple - in fact, this is an "optical illusion." More precisely - we used one trick. For example, to get the number 2.5, you can divide 5 by 2. And for this, we all at school taught the method of dividing the "corner". But let's take a closer look at this method. And then we find that the fakir acts as follows - it multiplies the dividend by a constant containing the divisor, or its factors. And then it reduces exactly the factors from the constant to the factors of the divisor. It looks like this:
That's all miracles - a deuce from a divider is reduced to a deuce from a constant which is equal to , and one five remained as a result, which is written in after the decimal separator. The number is never shared , it multiplies by from the amount . But we don’t see it, thanks to the very “optical illusion” that we trained from school to create independently during each division division operation. Well, isn't that a star? One had only to push the foliage over the muted representations from the time of elementary school, when we saw the light of something new, not quite ordinary, which is not taught at school (but in vain).
Let us now explain the “optical illusion” at a slightly higher level. We simply translated the division result into a format convenient for storage and perception. The number itself does not depend on the format. And the number of characters in it is also. We have already observed the possibility of putting brackets around a period, and thereby reduce the infinity to the length of the period and two brackets. And this is also a data format, but used for periodic fractions. And the format of finite fractions hides infinity by reducing by factors from the base of the decimal number system. If we take, for example, the ternary number system, then the division of 5 by 2 will look like this:
That is, we got infinity in the form of a periodic fraction, because now we used another constant that does not contain factors that can be reduced with the number 2. But in a hexadecimal system the result would again become final - 2.3. But the number itself remains somewhere in the shade, and probably the best record for it would be 5/2, and everything else is the matter of choosing the presentation format for this number.
Now about infinite fractions. Periodic ones are obtained by dividing integers, and irrational ones (with infinite period length) are obtained by calculating a root of some degree from an integer. That is, people derived two categories of division from the abstraction of integers - with different factors and with the same ones. The first option allows you to divide any integer into any other integer, but sometimes it gives a fractional result. The second option allows you to divide the numbers only into those that are exactly equal to the result of division (including multiple for roots of large degrees). In general, we have the same division, but without limitation on the result and with the restriction. The restriction leads us to two options: either reduce the divisor with a factor from the dividend (and then you can get an integer equal to the divisor), or divide the irreducible dividend by a certain number. What then can be a "certain number"? If it is an integer, then as a result we get a fraction (the dividend and divisor are irreducible), which is not equal to an integer. Therefore, since integers do not fit, you need to look for a fraction that would be equal to the result. Finite fractions also disappear, because they actually represent a number of the form which, when multiplied by itself, would give us a new fraction of the form , which again gives us a finite or periodic fraction, and not an integer. Therefore, it is necessary to select a fraction that would reduce the ratio of their squares to an integer with an infinite growth of N and M. Why for infinite integers the ratio can be made whole, but not for the end? Because the more numbers, the less influence on the result is their discreteness. The integer following any chosen one is necessarily different from it by one. And this unit does not allow you to precisely set the desired result, because, for example, between 1/1000 and 2/1000 there are infinitely many numbers, for example 11/10000 or 145/100000, etc. Therefore, increasing the length of the number, it is possible at infinity to obtain any result with any accuracy. And then multiply it by itself and get an integer. And at the same time, the period of such a fraction really becomes infinite, as we will see later. And an infinite period is the property of an irrational number, to which we have passed from completely rational numbers. Here is such a starry light, smoothly turning into the darkness of infinity.
But why do we need this junction between two classes of numbers? Maybe one is enough? Let's try to simulate. So we got exactly the root of an integer, found two large integers tending to infinity, which, when squared and divided by each other, give an integer. Now add one to any of these infinitely large numbers. What will happen then? In our usual language, we got a definition for a new number, which is not periodic (because it has an infinite period) and at the same time is not the root of the whole. That is, the new number does not fit into the classification given to us from rational and irrational numbers. And now all such numbers were called by mathematicians transcendental, after all it is necessary to put them somewhere. But an interesting point - at first there were roots from integers, called irrational numbers, and then “other” numbers appeared. That is, first, for the sake of the ancient Greek tradition, the overestimation of the importance of integers was all classified precisely on the basis of methods of obtaining from integers. The first method was division and rational numbers derived from it. Then people met with roots. So there were irrational numbers. And in addition to the rational and the irrational, a third category arose. Moreover, the third category at first was a terrible rarity that Euler discovered, but besides the Euler discovery, there were simply no others like that. And it was decided to divide the irrational into two classes - algebraic (that is, growing from the roots) and transcendental (special, outstanding, going beyond, because only Euler could find them).But in the future, numbers that did not originate from the roots became massive, and mathematicians even determined that there were many more than algebraic ones. Therefore, the transcendence (feature) of such numbers has become only a tribute to tradition. Although if we recall the concept of correlation, then all these rational, irrational, algebraic and transcendental ones immediately become artificial names for a very conditional division of numbers resulting from a simple displacement of the end of one of the compared segments. Well, with such an approach, transcendental numbers simply become “the rest”, that is, if, from the relations of segments, for the sake of maintaining the tradition of extracting integers, we select the classes obtained by the operations of dividing and extracting the root from integers, we get only rational and algebraic, but all the rest are transcendental.That is, in total there are only three categories of infinite fractions. Therefore, the name "transcendental" becomes somewhat strained, do not you? Well, okay, because tradition is our everything, even in such an exact science as mathematics.
That's all for now. In the next series, let's talk about rational stars.
Further, in several series, a story will be followed about things that are accessible to any high school graduate (and even many schoolchildren). There will be no evidence, since they are often obvious, and if presented here would not only stretch the volume, but would also scare away many readers.

First series
First there were stars. There was a process of playing with them, looking at and feeling, tossing up and observing a shining fall path. The stars were patterns. And the sandbox was numbers. The numbers turned on a new side, and another star appeared in the gaps between them. Her radiance attracted and, best of all, did not burn, but allowed herself to be touched, picked up, and then waved to them in order to leave a sparkling trace of stardust. But then the stars became familiar and there was only one job left to sort them. And then an idea came up.
The idea was simple - you can make money on it. And yes, it really motivated. But it did not grow together. It was entertaining, there were regular stars shining in a new way, there was pleasure and there was progress. Only in the end did a forest arise, a continuous forest of shining trees. And I was weak, I could not sort this taiga in search of true light, because there are millions of trees, and I am alone. Therefore, I suggest you look at the stars, and if they are interesting, then you can earn $ 400K, but the truth is there is one “but” - in the forest you need to be able to choose the right path.
On the approaches to the stars
What is a number? On the one hand, it is a product of our gloomy mind, not found in nature. But on the other hand, such an abstraction allows us to simulate many processes that we observe all in the same nature. Only the model is not equal to the observed phenomenon. So again we are dealing with adaptation to our modest capabilities of the ways of describing nature. Is it good? In terms of accuracy, the description is not very good. Not because someone may not have enough decimal places, but because an inaccurately modeled phenomenon can surprise us a lot when it turns out that the model lacks one specific feature or another, which is present in reality and can sometimes make a little noise inattentive naturalists on the head.
In light of the foregoing, let us try to inquire about the completeness of the basis of any modeling - the completeness of understanding the concept of number. Just a number, just knowledge about it, laid down from early childhood, it seems - well, what else could it be? But just there we can find the abyss. Yes, the one that is without a bottom, and which is full of stars.
There are no numbers in nature. But in nature you can see the relationship. The cloud is larger (longer / wider / thicker / like_you_ else_will_be_becoming) another cloud, which means there is a place for correlation. But the ratio also has no numbers. There are only two clouds, one more, the other less, and there is their ratio. Although yes, the ratio was also invented by man. Therefore, one may ask - what is the use of it? The benefit is this - the concept of correlation is one step ahead of the concept of number. At first there was a ratio, and only then did a number appear. More precisely - fractional numbers. Therefore, understanding the relationship, we will understand the numbers.
How are fractional numbers obtained? Very simple - from the need to model correlation. At first there were ratios of steps and sides of land, sheep from one owner to sheep from another, the weight of one watermelon to the weight of another. In all these cases, there was a need to somehow express the difference. But the difference was not divided strictly by the number of steps or the size of the neighboring watermelon. At first they learned to express the difference by dividing them into smaller units of measure (elbows were added to the steps, and fingers were added to the elbows). But science did not stand still and demanded ever greater accuracy. As a result, everyone agreed on uniformity, forgetting about fingers, elbows, steps and other pounds with sterling. Uniformity is expressed in number.
How to correlate two segments if one of them does not fit into the other an integer number of times? You can measure with your fingers, but it will be more accurate to take a smaller segment as a unit of measurement and divide it into identical parts. With these parts, you can measure that part of a larger segment that is not measured by the entire smaller segment. But then a new part of the larger segment arises, which is no longer measurable by the selected parts. We apply recursion and again break the already broken parts into even smaller components. We measure them previously immeasurable. And again we get an immeasurable remainder. Divide the parts again, measure again. Again we get the remainder. But you can get bored!
As a result, people came up with the idea of rounding and stopped re-dividing the unit of measurement. That is, people scored on accuracy (they say it is sufficient). But nature does not forgive inaccuracies in modeling.
How are ratios modeled today? They are modeled using the classification of fractional numbers. The classification is this - there are integers and there are fractional numbers. Whole ones are unstable, but fractional ones are divided into finite and infinite fractions. For the time being, we also forget about the final ones. Infinite are divided into rational and irrational. We usually forget about the first part. The irrational are divided into algebraic and transcendental. Everything, no more divisions. But for clarity, we give a classification in the form of a picture:

Why is this classification bad? She's not that bad. She, as Winnie the Pooh used to say, is good, but somehow lame ... That is, it is clear that with the accuracy of the expression of values, she is not all right because of infinity. But there is another side to the coin. This side (in this context) is called "divisibility". We cannot precisely separate two numbers (one on another) because we rest against infinity. But then we are interested in such phenomena from the world of numbers as simplicity and the number of divisors that eliminate infinity when they appear. Prime numbers form the basis of the number series of integers. And these important numbers (including, for example, for comfort when remotely paying for services) numbers are very dependent on the division operation. And division often gives us fractions. And fractions give us fractional numbers. Well, for fractional numbers, someone gave us the previously given classification of finite, infinite, rational, irrational, algebraic and transcendental. But does this classification give us the opportunity to find answers to questions about numbers? For example, about the same simple ones? Or about fractional? It seems to give, but not as much as we would like.
Take prime numbers. Today, the maximum prime numbers are searched in essence by exhaustive search. That is, they take the candidate number, and then check whether it is simple or not. Candidates get numbers simply - if you know the method of checking simplicity for a certain class of numbers, then here is the list of candidates in the form of representatives of the class that they go through stupidly in a row, checking each number, starting, of course, with small values. And so far they have come to numbers of the order of two to the degree of eighty-odd million. This is a number of almost twenty-five million decimal places. In principle, it looks impressive. But what prevents us from recalling the slogan “higher, further, faster”?
Fundamentally, we are hindered by a lack of understanding. Yes, our model of the phenomenon called “number” is incomplete. And yes, the part of the model called “division” is most incomplete. Therefore, eighty million units in computer memory is the limit for humanity. Why units? Because it looks like the biggest prime numbers. These are one units, but in binary notation. For them, there is the Luc-Lemer test, which shows us a simple number or a compound. And this test requires years of work of one processor core to check one candidate number of eighty million binary units. Only eighty megabytes, or ten megabytes, and humanity is no longer able to step further. What is ten megabytes? This is a penny, this is a trifle, it is almost nothing for modern computers. But the test has been going on for years. Therefore, you have to run it on millions of computers on which volunteers install the appropriate program, and as a result check one candidate number for a certain number of seconds (and this if there are a lot of volunteers). But the problem is that there are a lot of candidate numbers, and therefore it takes many months to find the next prime number. And with such deliberation, one can expect that the movement of only up to hundreds of millions of binary units will take ten years.
Is it possible to speed up the process? Can. But more understanding is needed. For example - how to reduce the time to test each number? So far, such a decrease is achieved by massaging iron. Or the second option - you can offer a quicker test of simplicity. But with this for about 100 years, little has changed. And yet, if you figure it out, then maybe it will work out with us. Only need to understand from the very basics.
Stars near
Thinking about the relationships, everyone can contribute a lot to science. Just being curious is enough. For example, one may ask, why is the classification of fractional numbers just this? And find the answer in a thought experiment to measure the ratio of the same segments. First, the segments are correlated as 1 to 2. This ratio is understandable, it gives us the number 2, which shows how many times the larger segment exceeds the smaller. And now let’s lengthen a slightly smaller segment. What will happen? The ratio will cease to be whole. The excess obtained from lengthening prevents us from obtaining a simple answer in the problem. But we can use it as a ruler. If it fits an integer number of times in half a larger segment, then we can express the ratio through this integer. So we get the ratio:
where N is the number of times it takes to fit the excess from stretching the smaller length into half the larger length. So we got a rational number. It is always given by the ratio of integers. If we now lengthen the smaller segment a little more, then we can get a situation where no matter how much we multiply the smaller segment by a certain integer, we cannot get an exact match with a certain number of lengths of the larger segment. So we got an irrational number that characterizes the new ratio. Note that a microscopic shift of the segment boundary leads to an endless process of identifying the ratio of lengths. One step for the humble researcher and a huge change for number theory - a new element in the classification is required. One step and - from micro-size right to infinity. From one category of numbers to a completely new one, fundamentally incompatible with the previous one. Isn't that a star?
But in fact, we just slightly changed one segment. So where did the fundamentally new category come from? In general, classification is important for its ability to exactly match reality. But what kind of accuracy came along with irrational numbers? They allow you to model any ratio, and not just the ratio of integers, so it really makes sense to separate such classes. But this is not all accuracy, because I want to understand all these infinities, how they appear, what they mean and why they exist at all. True, with infinities, everything is not easy, but because for now we will deal with finite relationships. It seems that everything is simple with them, take N, divide it by M, and get a fractional number. It will be very good if the number turns out to be short, for example 2.5 or 3.25. But more often to the world are relations of the form 4.12 (3456), that is, again with infinities, but these are infinities “in period”. Just by noticing repeating numbers, you can write down a number from an infinite number of characters very simply and compactly. That's how we famously coped with infinity. Also a small asterisk. But this is only a cursory glance.
Now let's turn on curiosity and ask questions. And why are some fractional numbers finite and others infinite? And why are some types of infinite infinitely long, while others with a period? And why before the period in number 4.12 (3456) we see the numbers 1 and 2? And why does there exist a preperiod? And why in the period do we see numbers 3 and 4? And why is the period length in this example equal to four? And why is the number of numbers before the period equal to two? And we only superficially cast a curious look at just one fractional number. And for other numbers, the questions will be even more interesting.
Let's try to answer. Why are fractional numbers finite? Very simple - in fact, this is an "optical illusion." More precisely - we used one trick. For example, to get the number 2.5, you can divide 5 by 2. And for this, we all at school taught the method of dividing the "corner". But let's take a closer look at this method. And then we find that the fakir acts as follows - it multiplies the dividend by a constant containing the divisor, or its factors. And then it reduces exactly the factors from the constant to the factors of the divisor. It looks like this:
That's all miracles - a deuce from a divider is reduced to a deuce from a constant which is equal to , and one five remained as a result, which is written in after the decimal separator. The number is never shared , it multiplies by from the amount . But we don’t see it, thanks to the very “optical illusion” that we trained from school to create independently during each division division operation. Well, isn't that a star? One had only to push the foliage over the muted representations from the time of elementary school, when we saw the light of something new, not quite ordinary, which is not taught at school (but in vain).
Let us now explain the “optical illusion” at a slightly higher level. We simply translated the division result into a format convenient for storage and perception. The number itself does not depend on the format. And the number of characters in it is also. We have already observed the possibility of putting brackets around a period, and thereby reduce the infinity to the length of the period and two brackets. And this is also a data format, but used for periodic fractions. And the format of finite fractions hides infinity by reducing by factors from the base of the decimal number system. If we take, for example, the ternary number system, then the division of 5 by 2 will look like this:
That is, we got infinity in the form of a periodic fraction, because now we used another constant that does not contain factors that can be reduced with the number 2. But in a hexadecimal system the result would again become final - 2.3. But the number itself remains somewhere in the shade, and probably the best record for it would be 5/2, and everything else is the matter of choosing the presentation format for this number.
Now about infinite fractions. Periodic ones are obtained by dividing integers, and irrational ones (with infinite period length) are obtained by calculating a root of some degree from an integer. That is, people derived two categories of division from the abstraction of integers - with different factors and with the same ones. The first option allows you to divide any integer into any other integer, but sometimes it gives a fractional result. The second option allows you to divide the numbers only into those that are exactly equal to the result of division (including multiple for roots of large degrees). In general, we have the same division, but without limitation on the result and with the restriction. The restriction leads us to two options: either reduce the divisor with a factor from the dividend (and then you can get an integer equal to the divisor), or divide the irreducible dividend by a certain number. What then can be a "certain number"? If it is an integer, then as a result we get a fraction (the dividend and divisor are irreducible), which is not equal to an integer. Therefore, since integers do not fit, you need to look for a fraction that would be equal to the result. Finite fractions also disappear, because they actually represent a number of the form which, when multiplied by itself, would give us a new fraction of the form , which again gives us a finite or periodic fraction, and not an integer. Therefore, it is necessary to select a fraction that would reduce the ratio of their squares to an integer with an infinite growth of N and M. Why for infinite integers the ratio can be made whole, but not for the end? Because the more numbers, the less influence on the result is their discreteness. The integer following any chosen one is necessarily different from it by one. And this unit does not allow you to precisely set the desired result, because, for example, between 1/1000 and 2/1000 there are infinitely many numbers, for example 11/10000 or 145/100000, etc. Therefore, increasing the length of the number, it is possible at infinity to obtain any result with any accuracy. And then multiply it by itself and get an integer. And at the same time, the period of such a fraction really becomes infinite, as we will see later. And an infinite period is the property of an irrational number, to which we have passed from completely rational numbers. Here is such a starry light, smoothly turning into the darkness of infinity.
But why do we need this junction between two classes of numbers? Maybe one is enough? Let's try to simulate. So we got exactly the root of an integer, found two large integers tending to infinity, which, when squared and divided by each other, give an integer. Now add one to any of these infinitely large numbers. What will happen then? In our usual language, we got a definition for a new number, which is not periodic (because it has an infinite period) and at the same time is not the root of the whole. That is, the new number does not fit into the classification given to us from rational and irrational numbers. And now all such numbers were called by mathematicians transcendental, after all it is necessary to put them somewhere. But an interesting point - at first there were roots from integers, called irrational numbers, and then “other” numbers appeared. That is, first, for the sake of the ancient Greek tradition, the overestimation of the importance of integers was all classified precisely on the basis of methods of obtaining from integers. The first method was division and rational numbers derived from it. Then people met with roots. So there were irrational numbers. And in addition to the rational and the irrational, a third category arose. Moreover, the third category at first was a terrible rarity that Euler discovered, but besides the Euler discovery, there were simply no others like that. And it was decided to divide the irrational into two classes - algebraic (that is, growing from the roots) and transcendental (special, outstanding, going beyond, because only Euler could find them).But in the future, numbers that did not originate from the roots became massive, and mathematicians even determined that there were many more than algebraic ones. Therefore, the transcendence (feature) of such numbers has become only a tribute to tradition. Although if we recall the concept of correlation, then all these rational, irrational, algebraic and transcendental ones immediately become artificial names for a very conditional division of numbers resulting from a simple displacement of the end of one of the compared segments. Well, with such an approach, transcendental numbers simply become “the rest”, that is, if, from the relations of segments, for the sake of maintaining the tradition of extracting integers, we select the classes obtained by the operations of dividing and extracting the root from integers, we get only rational and algebraic, but all the rest are transcendental.That is, in total there are only three categories of infinite fractions. Therefore, the name "transcendental" becomes somewhat strained, do not you? Well, okay, because tradition is our everything, even in such an exact science as mathematics.
That's all for now. In the next series, let's talk about rational stars.
All Articles