Unpacking nested lists of indefinite depth
Today I would like to talk about unpacking nested lists of indefinite depth. This is a fairly non-trivial task, so I would like to talk here about what implementations are, their pros and cons and a comparison of their performance.
The article will consist of several sections below:
- Functions
- Data
- results
- findings
Part 1. Functions
Borrowed implementations
outer_flatten_1
def outer_flatten_1(array: Iterable) -> List: """ Based on C realization of this solution More on: https://iteration-utilities.readthedocs.io/en/latest/generated/deepflatten.html https://github.com/MSeifert04/iteration_utilities/blob/384948b4e82e41de47fa79fb73efc56c08549b01/src/deepflatten.c """ return deepflatten(array)
I took this function for parsing from an external package, iteration_utilities.
The implementation is done in C, leaving a high-level function call interface for python.
The implementation of the function in C is rather cumbersome, you can see it by clicking on the link in the spoiler. The function is an iterator.
>>> from typing import Iterator, Generator >>> from iteration_utilities import deepflatten >>> isinstance(deepflatten(a), Iterator) True >>> isinstance(deepflatten(a), Generator) False
It is difficult to say about the complexity of the algorithm implemented here, so I leave this interest to Habr users.
In general, I would also like to note that all other functions from this library are quite fast and are also implemented in C.
outer_flatten_2
def outer_flatten_2(array: Iterable) -> List: """ recursive algorithm, vaguely reminiscent of recursion_flatten. Based on next pattern: .. code:: python try: tree = iter(node) except TypeError: yield node more on: https://more-itertools.readthedocs.io/en/stable/api.html#more_itertools.collapse """ return collapse(array)
The implementation of this method of unpacking nested lists is also in the external package, namely more_itertools.
The function is performed on pure python, but not optimal, in my opinion. A detailed implementation can be seen in the documentation link .
The complexity of this algorithm is O (n * m).
Own implementation
niccolum_flatten
def niccolum_flatten(array: Iterable) -> List: """ Non recursive algorithm Based on pop/insert elements in current list """ new_array = array[:] ind = 0 while True: try: while isinstance(new_array[ind], list): item = new_array.pop(ind) for inner_item in reversed(item): new_array.insert(ind, inner_item) ind += 1 except IndexError: break return new_array
When it somehow came up in telegrams to the public @ru_python_beginners about the implementation of unpacking nested lists of indefinite nesting, I proposed my own option.
It consists in the fact that we copy the original list (so as not to change it), and then in the while True loop we check while the item is a list - we go through it and insert the result to the very beginning.
Yes, now I understand that it does not look optimal and difficult, because reindexing occurs each time (as we add and remove from the top of the list), however this option also has the right to life and we will check its implementation along with the rest.
The complexity of this algorithm is O (n ^ 3 * m) due to rebuilding the list twice for each iteration passed
tishka_flatten
def tishka_flatten(data: Iterable) -> List: """ Non recursive algorithm Based on append/extend elements to new list """ nested = True while nested: new = [] nested = False for i in data: if isinstance(i, list): new.extend(i) nested = True else: new.append(i) data = new return data
One of the first also showed Tishka17 implementation. It consists in the fact that inside the while nested loop iterates over the existing list with the key nested = False, and if it has at least once got a sheet, it leaves the nested = True flag and extend'it this sheet to the list. Accordingly, it turns out that for each run it lays out one level of nesting, how many levels of nesting there will be - there will be so many passes through the cycle. As can be seen from the description - not the most optimal algorithm, but still, it is different from the rest.
The complexity of this algorithm is O (n * m).
zart_flatten
def zart_flatten(a: Iterable) -> List: """ Non recursive algorithm Based on pop from old and append elements to new list """ queue, out = [a], [] while queue: elem = queue.pop(-1) if isinstance(elem, list): queue.extend(elem) else: out.append(elem) return out[::-1]
An algorithm also suggested by one of the experienced chat participants. In my opinion, it is quite simple and clean. Its meaning is that if the element is a list, we add the result to the end of the original list, and if not, we add it to the output. I will call it below the extend / append mechanism. As a result, we display the inverted resulting resulting flat list in order to preserve the original order of the elements.
The complexity of this algorithm is O (n * m).
recursive_flatten_iterator
def recursive_flatten_iterator(arr: Iterable) -> Iterator: """ Recursive algorithm based on iterator Usual solution to this problem """ for i in arr: if isinstance(i, list): yield from recursion_flatten(i) else: yield i
Probably the most common solution to this problem is through recursion and yield from. Little can be said - the algorithm seems quite simple and efficient, apart from the fact that it is done through recursion and, with large enclosures, there can be a fairly large stack of calls.
The complexity of this algorithm is O (n * m).
recursive_flatten_generator
def recursive_flatten_generator(array: Iterable) -> List: """ Recursive algorithm Looks like recursive_flatten_iterator, but with extend/append """ lst = [] for i in array: if isinstance(i, list): lst.extend(recursive_flatten_list(i)) else: lst.append(i) return lst
This function is quite similar to the preceding one, it is only executed not through an iterator, but through a recursive extend / append mechanism.
The complexity of this algorithm is O (n * m).
tishka_flatten_with_stack
def tishka_flatten_with_stack(seq: Iterable) -> List: """ Non recursive algorithm Based on zart_flatten, but build on try/except pattern """ stack = [iter(seq)] new = [] while stack: i = stack.pop() try: while True: data = next(i) if isinstance(data, list): stack.append(i) i = iter(data) else: new.append(data) except StopIteration: pass return new
Another algorithm provided by Tishka, which, in fact, is very similar to zart_flatten, however, it was implemented there through a simple extend / append mechanism, then through iteration in an infinite loop in which this mechanism is used. Thus it turned out something similar to zart_flatten, but through iteration and while True.
The complexity of this algorithm is O (n * m).
Part 2. Data
To test the effectiveness of these algorithms, we need to create functions for the automatic generation of lists of a certain nesting, which I have successfully dealt with and will show you the result below:
create_data_decreasing_depth
def create_data_decreasing_depth( data: Union[List, Iterator], length: int, max_depth: int, _current_depth: int = None, _result: List = None ) -> List: """ creates data in depth on decreasing. Examples: >>> data = create_data_decreasing_depth(list(range(1, 11)), length=5, max_depth=3) >>> assert data == [[[1, 2, 3, 4, 5], 6, 7, 8, 9, 10]] >>> data = create_data_decreasing_depth(list(range(1, 11)), length=2, max_depth=3) >>> assert data == [[[1, 2], 3, 4], 5, 6], [[7, 8,] 9, 10]] """ _result = _result or [] _current_depth = _current_depth or max_depth data = iter(data) if _current_depth - 1: _result.append(create_data_decreasing_depth( data=data, length=length, max_depth=max_depth, _current_depth=_current_depth - 1, _result=_result)) try: _current_length = length while _current_length: item = next(data) _result.append(item) _current_length -= 1 if max_depth == _current_depth: _result += create_data_decreasing_depth( data=data, length=length, max_depth=max_depth) return _result except StopIteration: return _result
This function creates nested lists with decreasing nesting.
>>> data = create_data_decreasing_depth(list(range(1, 11)), length=5, max_depth=3) >>> assert data == [[[1, 2, 3, 4, 5], 6, 7, 8, 9, 10]] >>> data = create_data_decreasing_depth(list(range(1, 11)), length=2, max_depth=3) >>> assert data == [[[1, 2], 3, 4], 5, 6], [[7, 8,] 9, 10]]
create_data_increasing_depth
def create_data_increasing_depth( data: Union[List, Iterator], length: int, max_depth: int, _current_depth: int = None, _result: List = None ) -> List: """ creates data in depth to increase. Examples: >>> data = create_data_increasing_depth(list(range(1, 11)), length=5, max_depth=3) >>> assert data == [1, 2, 3, 4, 5, [6, 7, 8, 9, 10]] >>> data = create_data_increasing_depth(list(range(1, 11)), length=2, max_depth=3) >>> assert data == [1, 2, [3, 4, [5, 6]]], 7, 8, [9, 10]] """ _result = _result or [] _current_depth = _current_depth or max_depth data = iter(data) try: _current_length = length while _current_length: item = next(data) _result.append(item) _current_length -= 1 except StopIteration: return _result if _current_depth - 1: tmp_res = create_data_increasing_depth( data=data, length=length, max_depth=max_depth, _current_depth=_current_depth - 1) if tmp_res: _result.append(tmp_res) if max_depth == _current_depth: tmp_res = create_data_increasing_depth( data=data, length=length, max_depth=max_depth) if tmp_res: _result += tmp_res return _result
This function creates nested lists with increasing nesting.
>>> data = create_data_increasing_depth(list(range(1, 11)), length=5, max_depth=3) >>> assert data == [1, 2, 3, 4, 5, [6, 7, 8, 9, 10]] >>> data = create_data_increasing_depth(list(range(1, 11)), length=2, max_depth=3) >>> assert data == [1, 2, [3, 4, [5, 6]]], 7, 8, [9, 10]]
generate_data
def generate_data() -> List[Tuple[str, Dict[str, Union[range, Num]]]]: """ Generated collections of Data by pattern {amount_item}_amount_{length}_length_{max_depth}_max_depth where: .. py:attribute:: amount_item: len of flatten elements .. py:attribute:: length: len of elements at the same level of nesting .. py:attribute:: max_depth: highest possible level of nesting """ data = [] amount_of_elements = [10 ** i for i in range(5)] data_template = '{amount_item}_amount_{length}_length_{max_depth}_max_depth' # amount_item doesn't need to be [1] for amount_item in amount_of_elements[1:]: for max_depth in amount_of_elements: # for exclude flatten list after generate data by create_data_increasing_depth if amount_item > max_depth: # generate four types of length for length in range(0, max_depth + 1, math.ceil(max_depth / 4)): # min length must be 1 length = length or 1 data_name = data_template.format( amount_item=amount_item, length=length, max_depth=max_depth ) data_value = { 'data': range(amount_item), 'length': length, 'max_depth': max_depth } data.append((data_name, data_value)) # for not to produce more than 1 flat entity if max_depth == 1: break # this order is convenient for me data = sorted(data, key=lambda x: [x[1]['data'][-1], x[1]['max_depth'], x[1]['length']]) return data
This function directly creates patterns for test data. To do this, it generates headers created by the template.
data_template = '{amount_item}_amount_{length}_length_{max_depth}_max_depth'
Where:
- amount - the total number of items in the list
- length - the number of elements at one nesting level
- max_depth - maximum number of nesting levels
The data itself is transferred to the functions above to generate the necessary data. Accordingly, the output, as we will see later, we will have the following data (headers):
10_amount_1_length_1_max_depth 100_amount_1_length_1_max_depth 100_amount_1_length_10_max_depth 100_amount_3_length_10_max_depth 100_amount_6_length_10_max_depth 100_amount_9_length_10_max_depth 1000_amount_1_length_1_max_depth 1000_amount_1_length_10_max_depth 1000_amount_3_length_10_max_depth 1000_amount_6_length_10_max_depth 1000_amount_9_length_10_max_depth 1000_amount_1_length_100_max_depth 1000_amount_25_length_100_max_depth 1000_amount_50_length_100_max_depth 1000_amount_75_length_100_max_depth 1000_amount_100_length_100_max_depth 10000_amount_1_length_1_max_depth 10000_amount_1_length_10_max_depth 10000_amount_3_length_10_max_depth 10000_amount_6_length_10_max_depth 10000_amount_9_length_10_max_depth 10000_amount_1_length_100_max_depth 10000_amount_25_length_100_max_depth 10000_amount_50_length_100_max_depth 10000_amount_75_length_100_max_depth 10000_amount_100_length_100_max_depth 10000_amount_1_length_1000_max_depth 10000_amount_250_length_1000_max_depth 10000_amount_500_length_1000_max_depth 10000_amount_750_length_1000_max_depth 10000_amount_1000_length_1000_max_depth
Part 3. Results
To profile the CPU - I used line_profiler
For graphing - timeit + matplotlib
CPU Profiler
$ kernprof -l funcs.py $ python -m line_profiler funcs.py.lprof Timer unit: 1e-06 s Total time: 1.7e-05 s File: funcs.py Function: outer_flatten_1 at line 11 Line # Hits Time Per Hit % Time Line Contents ============================================================== 11 @profile 12 def outer_flatten_1(array: Iterable) -> List: 13 """ 14 Based on C realization of this solution 15 More on: 16 17 https://iteration-utilities.readthedocs.io/en/latest/generated/deepflatten.html 18 19 https://github.com/MSeifert04/iteration_utilities/blob/384948b4e82e41de47fa79fb73efc56c08549b01/src/deepflatten.c 20 """ 21 2 17.0 8.5 100.0 return deepflatten(array) Total time: 3.3e-05 s File: funcs.py Function: outer_flatten_2 at line 24 Line # Hits Time Per Hit % Time Line Contents ============================================================== 24 @profile 25 def outer_flatten_2(array: Iterable) -> List: 26 """ 27 recursive algorithm, vaguely reminiscent of recursion_flatten. Based on next pattern: 28 29 .. code:: python 30 31 try: 32 tree = iter(node) 33 except TypeError: 34 yield node 35 36 more on: 37 https://more-itertools.readthedocs.io/en/stable/api.html#more_itertools.collapse 38 """ 39 2 33.0 16.5 100.0 return collapse(array) Total time: 0.105099 s File: funcs.py Function: niccolum_flatten at line 42 Line # Hits Time Per Hit % Time Line Contents ============================================================== 42 @profile 43 def niccolum_flatten(array: Iterable) -> List: 44 """ 45 Non recursive algorithm 46 Based on pop/insert elements in current list 47 """ 48 49 2 39.0 19.5 0.0 new_array = array[:] 50 2 6.0 3.0 0.0 ind = 0 51 2 2.0 1.0 0.0 while True: 52 20002 7778.0 0.4 7.4 try: 53 21010 13528.0 0.6 12.9 while isinstance(new_array[ind], list): 54 1008 1520.0 1.5 1.4 item = new_array.pop(ind) 55 21014 13423.0 0.6 12.8 for inner_item in reversed(item): 56 20006 59375.0 3.0 56.5 new_array.insert(ind, inner_item) 57 20000 9423.0 0.5 9.0 ind += 1 58 2 2.0 1.0 0.0 except IndexError: 59 2 2.0 1.0 0.0 break 60 2 1.0 0.5 0.0 return new_array Total time: 0.137481 s File: funcs.py Function: tishka_flatten at line 63 Line # Hits Time Per Hit % Time Line Contents ============================================================== 63 @profile 64 def tishka_flatten(data: Iterable) -> List: 65 """ 66 Non recursive algorithm 67 Based on append/extend elements to new list 68 69 """ 70 2 17.0 8.5 0.0 nested = True 71 1012 1044.0 1.0 0.8 while nested: 72 1010 1063.0 1.1 0.8 new = [] 73 1010 992.0 1.0 0.7 nested = False 74 112018 38090.0 0.3 27.7 for i in data: 75 111008 50247.0 0.5 36.5 if isinstance(i, list): 76 1008 1431.0 1.4 1.0 new.extend(i) 77 1008 1138.0 1.1 0.8 nested = True 78 else: 79 110000 42052.0 0.4 30.6 new.append(i) 80 1010 1406.0 1.4 1.0 data = new 81 2 1.0 0.5 0.0 return data Total time: 0.062931 s File: funcs.py Function: zart_flatten at line 84 Line # Hits Time Per Hit % Time Line Contents ============================================================== 84 @profile 85 def zart_flatten(a: Iterable) -> List: 86 """ 87 Non recursive algorithm 88 Based on pop from old and append elements to new list 89 """ 90 2 20.0 10.0 0.0 queue, out = [a], [] 91 21012 12866.0 0.6 20.4 while queue: 92 21010 16849.0 0.8 26.8 elem = queue.pop(-1) 93 21010 17768.0 0.8 28.2 if isinstance(elem, list): 94 1010 1562.0 1.5 2.5 queue.extend(elem) 95 else: 96 20000 13813.0 0.7 21.9 out.append(elem) 97 2 53.0 26.5 0.1 return out[::-1] Total time: 0.052754 s File: funcs.py Function: recursive_flatten_generator at line 100 Line # Hits Time Per Hit % Time Line Contents ============================================================== 100 @profile 101 def recursive_flatten_generator(array: Iterable) -> List: 102 """ 103 Recursive algorithm 104 Looks like recursive_flatten_iterator, but with extend/append 105 106 """ 107 1010 1569.0 1.6 3.0 lst = [] 108 22018 13565.0 0.6 25.7 for i in array: 109 21008 17060.0 0.8 32.3 if isinstance(i, list): 110 1008 6624.0 6.6 12.6 lst.extend(recursive_flatten_generator(i)) 111 else: 112 20000 13622.0 0.7 25.8 lst.append(i) 113 1010 314.0 0.3 0.6 return lst Total time: 0.054103 s File: funcs.py Function: recursive_flatten_iterator at line 116 Line # Hits Time Per Hit % Time Line Contents ============================================================== 116 @profile 117 def recursive_flatten_iterator(arr: Iterable) -> Iterator: 118 """ 119 Recursive algorithm based on iterator 120 Usual solution to this problem 121 122 """ 123 124 22018 20200.0 0.9 37.3 for i in arr: 125 21008 19363.0 0.9 35.8 if isinstance(i, list): 126 1008 6856.0 6.8 12.7 yield from recursive_flatten_iterator(i) 127 else: 128 20000 7684.0 0.4 14.2 yield i Total time: 0.056111 s File: funcs.py Function: tishka_flatten_with_stack at line 131 Line # Hits Time Per Hit % Time Line Contents ============================================================== 131 @profile 132 def tishka_flatten_with_stack(seq: Iterable) -> List: 133 """ 134 Non recursive algorithm 135 Based on zart_flatten, but build on try/except pattern 136 """ 137 2 24.0 12.0 0.0 stack = [iter(seq)] 138 2 5.0 2.5 0.0 new = [] 139 1012 357.0 0.4 0.6 while stack: 140 1010 435.0 0.4 0.8 i = stack.pop() 141 1010 328.0 0.3 0.6 try: 142 1010 330.0 0.3 0.6 while True: 143 22018 17272.0 0.8 30.8 data = next(i) 144 21008 18951.0 0.9 33.8 if isinstance(data, list): 145 1008 997.0 1.0 1.8 stack.append(i) 146 1008 1205.0 1.2 2.1 i = iter(data) 147 else: 148 20000 15413.0 0.8 27.5 new.append(data) 149 1010 425.0 0.4 0.8 except StopIteration: 150 1010 368.0 0.4 0.7 pass 151 2 1.0 0.5 0.0 return new
Graphs
Overall result:
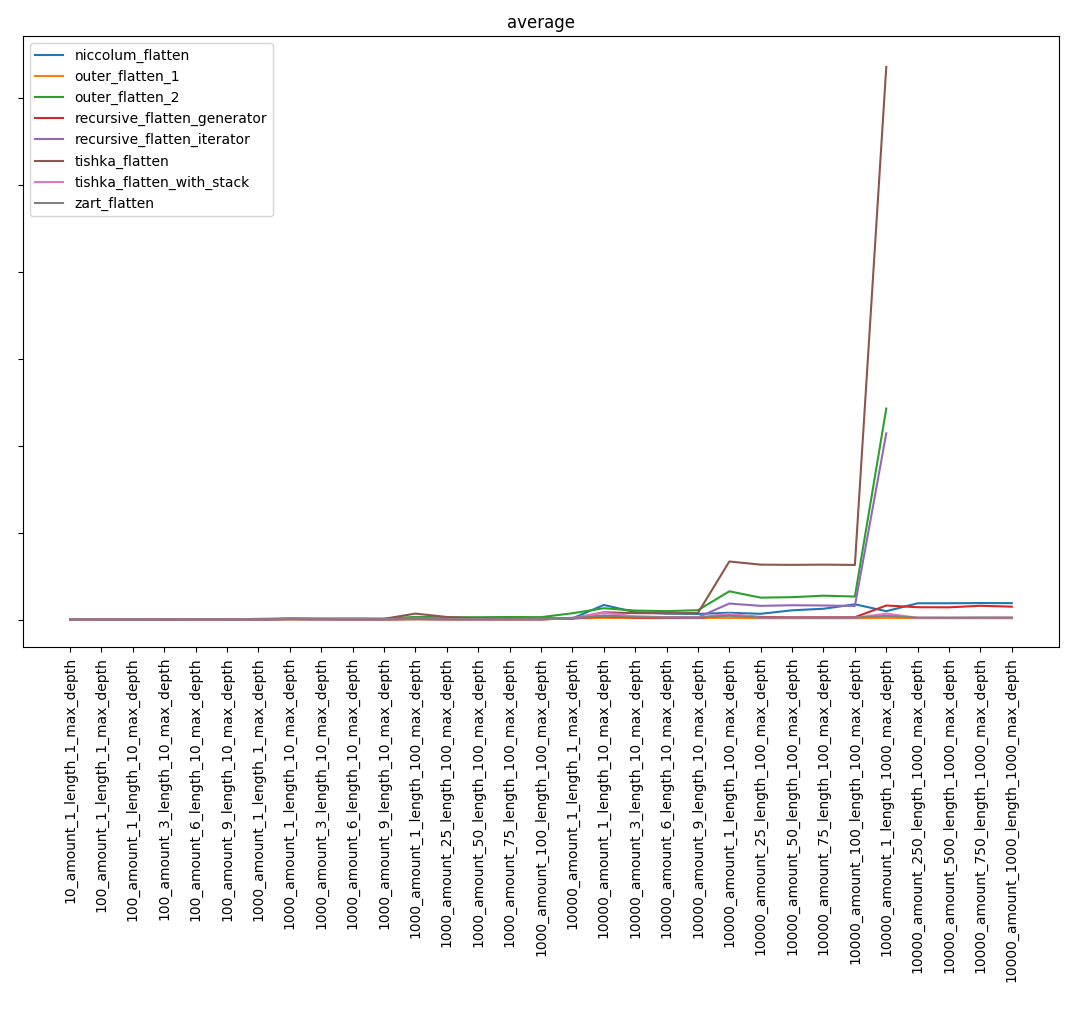
Excluding the slowest functions, we get:
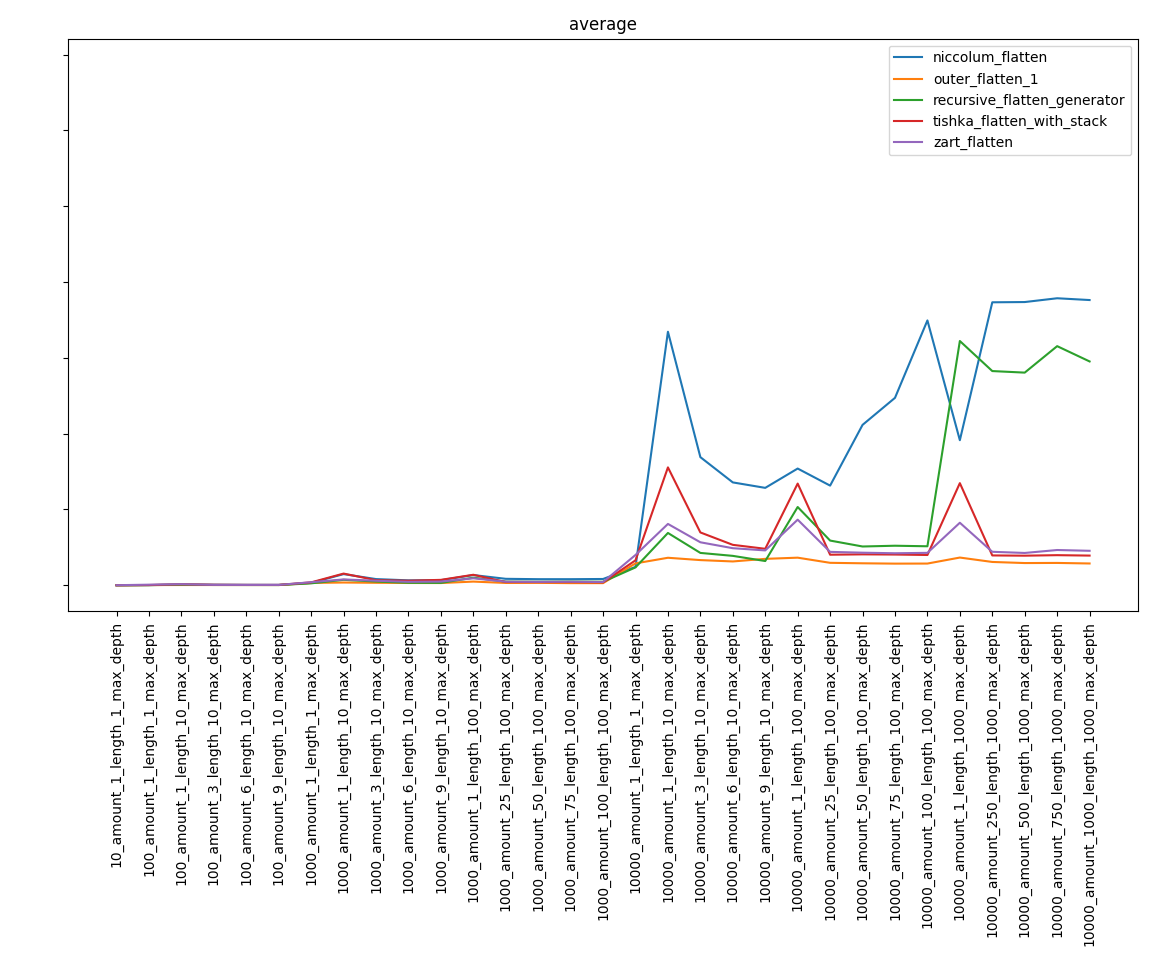
Part 4. Conclusions
Perhaps I will say the obvious thing, but, despite the known complexity of the algorithms, the result may not be obvious. So, the niccolum_flatten function, whose complexity was the highest, fell into the final stage and took far from the last place. And recursive_flatten_generator turned out to be much faster than recursive_flatten_iterator.
To summarize, I want to say first of all that this was more of a study than a guide to writing effective list unpacking algorithms. Usually, you can write the simplest implementation without thinking whether it is the fastest, because little savings.
useful links
More complete results can be found here.
Repository with code here
Sphinx documentation here
If you find errors, write to Niccolum telegram or to lastsal@mail.ru.
I will be glad to constructive criticism.
All Articles