New hint search service on hh.ru
Search hints are great. How often do we type the full site address in the address bar? And the name of the product in the online store? For such short queries, typing a few characters is usually enough if the search hints are good. And if you do not have twenty fingers or incredible typing speed, then you will surely use them.
In this article, we will talk about our new hh.ru search hint service, which we did in the previous issue of the School of Programmers .
The old service had a number of problems:

In the new service, we fixed these shortcomings (while adding new ones).
When there are no hints at all, you can manually select the top-N queries of users and generate hints from these queries using the exact occurrence of words (with or without order). This is a good option - it is easy to implement, gives good accuracy of prompts and does not experience performance problems. For a long time, our sajest worked like that, but a significant drawback of this approach is the insufficient completeness of issuance.
For example, the request “javascript developer” didn’t fall into such a list, so when we enter “javascript times” we have nothing to show. If we supplement the request, taking into account only the last word, we will see "javascript handyman" in the first place. For the same reason, it will not be possible to implement error correction more difficult than the standard approach with finding the closest words by Damerau-Levenshtein distance.
Another approach is to learn to evaluate the probabilities of queries and to generate the most probable continuations for a user query. To do this, use language models - a probability distribution on a set of word sequences.
Since user requests are mostly short, we did not even try neural network language models, but limited ourselves to n-gram:
As the simplest model, we can take the statistical definition of probability, then
However, such a model is not suitable for evaluating queries that were not in our sample: if we did not observe the 'junior developer java', then it turns out that
To solve this problem, you can use various models of smoothing and interpolation. We used Backoff:
Where P is the smoothed probability (we used Laplace smoothing):
where V is our dictionary.
So, we can evaluate the probability of a particular request, but how to generate these same requests? It is wise to do the following: let the user enter a query , then the queries that are suitable for us can be found from the condition
Of course, sorting through It’s not possible to select the best options for each incoming request, therefore we use Beam Search . For our n-gram language model, it comes down to the following algorithm:

Here the nodes highlighted in green are the final selected options, the number in front of the node - probability , after the node - .
It has become much better, but in generate_candidates you need to quickly get N best terms for a given context. In the case of storing only the probabilities of n-grams, we need to go through the entire dictionary, calculate the probabilities of all possible phrases, and then sort them. Obviously, this will not take off for online queries.
To quickly obtain the N best conditional probability variants of the continuation of the phrase, we used boron in terms. In node coefficient stored , value and sorted by conditional probability list of terms together with . The special term eos marks the end of a phrase.
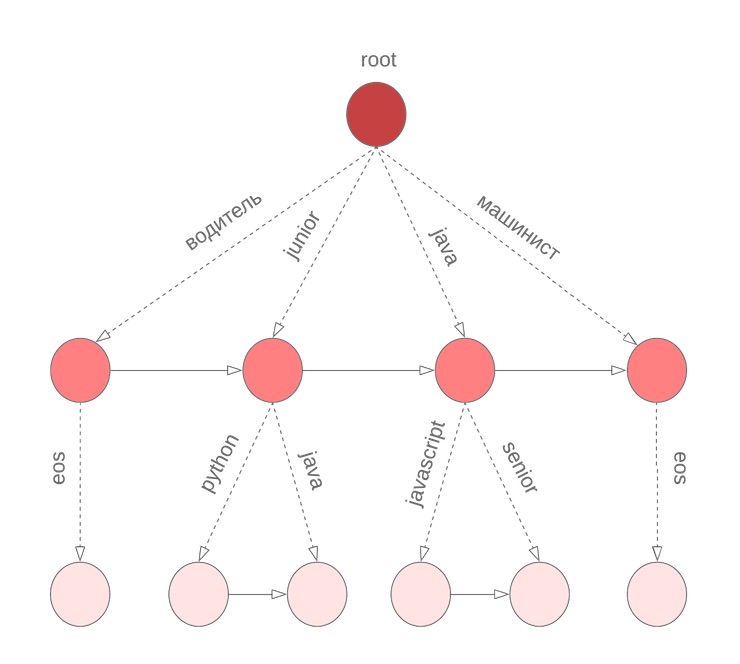
In the algorithm described above, we assume that all words in the query were completed. However, this is not true for the last word that the user enters it right now. We again need to go through the entire dictionary to continue the current word being entered. To solve this problem, we use a symbolic boron, in the nodes of which we store M terms sorted by the unigram probability. For example, this will look like our bor for java, junior, jupyter, javascript with M = 3:

Then, before beginning Beam Search, we find the M best candidates to continue the current word and select the N best candidates for .
Great, we have built a service that allows you to give good hints for a user request. We are even ready for new words. And everything would be fine ... But users take care and do not switch hfcrkflre keyboards.
How to solve this? The first thing that comes to mind is the search for corrections by finding the closest options for the Damerau-Levenshtein distance, which is defined as the minimum number of insertion / deletion / replacement of a character or transposition of two neighboring ones needed to get another from one line. Unfortunately, this distance does not take into account the probability of a particular replacement. So, for the introduced word “sapper”, we get that the options “collector” and “welder” are equivalent, although intuitively it seems that they had in mind the second word.
The second problem is that we do not take into account the context in which the error occurred. For example, in the query “order sapper” we should still prefer the option “collector” rather than “welder”.
If you approach the task of correcting typos from a probabilistic point of view, it is quite natural to come to a model of a noisy channel :
Then the correction task is set as finding the correct word w for input s. Depending on the source of the error, measure it can be built in different ways, in our case it’s wise to try to estimate the probability of typos (let's call them elementary replacements) , where t, r are symbolic n-grams, and then evaluate as the probability of getting s from w by the most probable elementary replacements.
Let be - splitting the string x into n substrings (possibly zero). The Brill-Moore model involves the calculation of probability in the following way:
But we need to find :
By learning to evaluate P (w | s), we will also solve the problem of ranking options with the same Damerau-Levenshtein distance and will be able to take into account the context when correcting a typo.
To calculate the probabilities of elementary substitutions, user queries will help us again: we will compose pairs of words (s, w) which
For such pairs, we consider the optimal alignment according to Levenshtein:
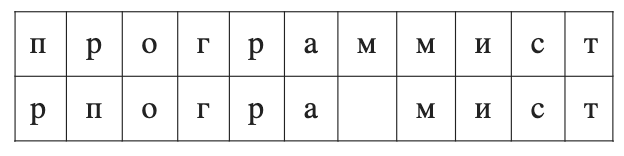
We compose all possible partitions of s and w (we limited ourselves to lengths n = 2, 3): n → n, pr → rn, pro → rn, ro → po, m → ``, mm → m, etc. For each n-gram, we find
Calculation directly takes : we need to sort through all possible partitions of w with all possible partitions of s. However, the dynamics on the prefix can give an answer for where n is the maximum length of elementary substitutions:
Here P is the probability of the corresponding row in the k-gram model. If you look closely, it is very similar to the Wagner-Fisher algorithm with Ukkonen clipping. At every step we get by enumerating all the fixes at provided and the choice of the most probable one.
So, we can calculate . Now we need to select several options w maximizing . More precisely, for the original request you must choose where maximum. Unfortunately, an honest choice of options did not fit into our response time requirements (and the project deadline was drawing to a close), so we decided to focus on the following approach:
For Clause 1.2, we used the FB-Trie algorithm (forward and backward trie), based on fuzzy search in the forward and reverse prefix trees. This turned out to be faster than evaluating P (s | w) throughout the dictionary.
With the construction of the language model, everything is simple: we collect statistics on user queries (how many times we made a request for a given phrase, how many users, how many registered users), we break down requests into n-grams and build burs. More complicated with the error model: at a minimum, a dictionary of the right words is needed to build it. As mentioned above, to select the training pairs, we used the assumption that such pairs should be close in Damerau-Levenshtein distance, and one should occur more often than the other several times.
But the data is still too noisy: xss injection attempts, incorrect layout, random text from the clipboard, experienced users with requests “programmer c not 1c”,requests from the cat that passed through the keyboard .
Therefore, to clear the source data, we excluded:
They also corrected the keyboard layout, checked against words from the texts of vacancies and open dictionaries. Of course, it was not possible to fix everything, but such options are usually either completely cut off or located at the bottom of the list.
Right before project protection, they launched a service in production for internal testing, and after a couple of days - for 20% of users. In hh.ru, all changes that are significant to users go through a system of AB tests , which allows us not only to be sure of the significance and quality of the changes, but also to find errors .
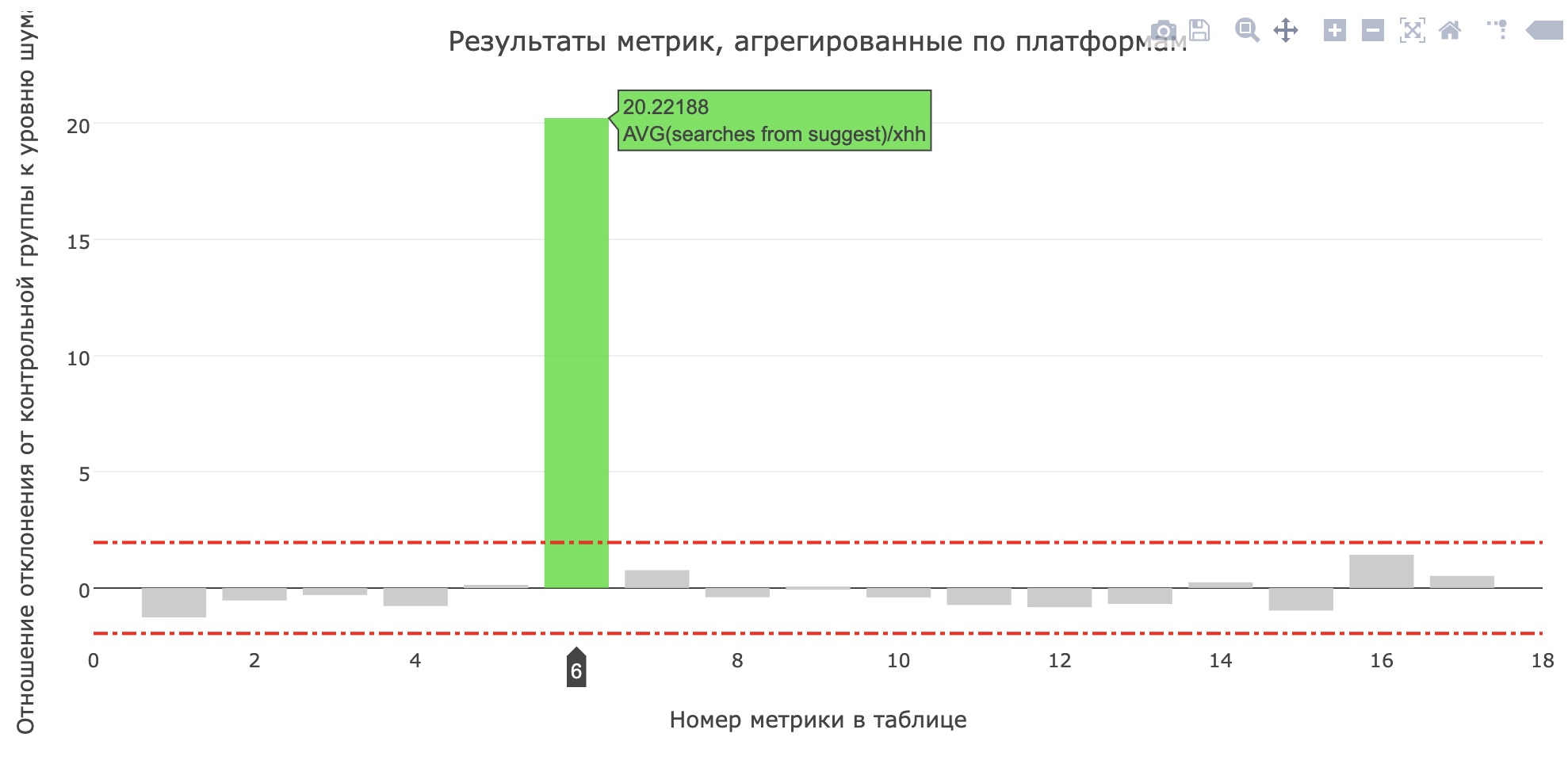
The metric of the average number of searches from the sujest to the applicants has brightened up (increased from 0.959 to 1.1355), and the share of searches from the sujest of all search queries has increased from 12.78% to 15.04%. Unfortunately, the main product metrics have not grown, but users have definitely become more likely to use tips.
There was no room for a story about the School's processes, other tested models, the tools that we wrote for model comparisons, and meetings where we decided which features to develop in order to catch up with the intermediate demos. Look at the records of the past school , leave a request at https://school.hh.ru , complete interesting tasks and come to study. By the way, the service for checking tasks was also done by the graduates of the previous set.
In this article, we will talk about our new hh.ru search hint service, which we did in the previous issue of the School of Programmers .
The old service had a number of problems:
- he worked on hand-selected popular user queries;
- could not adapt to changing user preferences;
- could not rank queries that are not included in the top;
- did not correct typos.

In the new service, we fixed these shortcomings (while adding new ones).
Dictionary of popular queries
When there are no hints at all, you can manually select the top-N queries of users and generate hints from these queries using the exact occurrence of words (with or without order). This is a good option - it is easy to implement, gives good accuracy of prompts and does not experience performance problems. For a long time, our sajest worked like that, but a significant drawback of this approach is the insufficient completeness of issuance.
For example, the request “javascript developer” didn’t fall into such a list, so when we enter “javascript times” we have nothing to show. If we supplement the request, taking into account only the last word, we will see "javascript handyman" in the first place. For the same reason, it will not be possible to implement error correction more difficult than the standard approach with finding the closest words by Damerau-Levenshtein distance.
Language model
Another approach is to learn to evaluate the probabilities of queries and to generate the most probable continuations for a user query. To do this, use language models - a probability distribution on a set of word sequences.

Since user requests are mostly short, we did not even try neural network language models, but limited ourselves to n-gram:
As the simplest model, we can take the statistical definition of probability, then
However, such a model is not suitable for evaluating queries that were not in our sample: if we did not observe the 'junior developer java', then it turns out that
To solve this problem, you can use various models of smoothing and interpolation. We used Backoff:
Where P is the smoothed probability (we used Laplace smoothing):
where V is our dictionary.
Option Generation
So, we can evaluate the probability of a particular request, but how to generate these same requests? It is wise to do the following: let the user enter a query , then the queries that are suitable for us can be found from the condition
Of course, sorting through It’s not possible to select the best options for each incoming request, therefore we use Beam Search . For our n-gram language model, it comes down to the following algorithm:
def beam(initial, vocabulary): variants = [initial] for i in range(P): candidates = [] for variant in variants: candidates.extends(generate_candidates(variant, vocabulary)) variants = sorted(candidates)[:N] return candidates def generate_candidates(variant, vocabulary): top_terms = [] # 1, 2, ... n for n0 in range(n): top_n = sorted(vocabulary, key=lambda c: P(|variant[-n0:]) top_terms.extends(top_n) candidates = [variant + [term] for term in top_terms] # candidates = sorted(candidates, key=lambda v: P(variant))[:N] return candidates

Here the nodes highlighted in green are the final selected options, the number in front of the node - probability , after the node - .
It has become much better, but in generate_candidates you need to quickly get N best terms for a given context. In the case of storing only the probabilities of n-grams, we need to go through the entire dictionary, calculate the probabilities of all possible phrases, and then sort them. Obviously, this will not take off for online queries.
Boron for probabilities
To quickly obtain the N best conditional probability variants of the continuation of the phrase, we used boron in terms. In node coefficient stored , value and sorted by conditional probability list of terms together with . The special term eos marks the end of a phrase.

But there is a nuance
In the algorithm described above, we assume that all words in the query were completed. However, this is not true for the last word that the user enters it right now. We again need to go through the entire dictionary to continue the current word being entered. To solve this problem, we use a symbolic boron, in the nodes of which we store M terms sorted by the unigram probability. For example, this will look like our bor for java, junior, jupyter, javascript with M = 3:

Then, before beginning Beam Search, we find the M best candidates to continue the current word and select the N best candidates for .
Typos
Great, we have built a service that allows you to give good hints for a user request. We are even ready for new words. And everything would be fine ... But users take care and do not switch hfcrkflre keyboards.
How to solve this? The first thing that comes to mind is the search for corrections by finding the closest options for the Damerau-Levenshtein distance, which is defined as the minimum number of insertion / deletion / replacement of a character or transposition of two neighboring ones needed to get another from one line. Unfortunately, this distance does not take into account the probability of a particular replacement. So, for the introduced word “sapper”, we get that the options “collector” and “welder” are equivalent, although intuitively it seems that they had in mind the second word.
The second problem is that we do not take into account the context in which the error occurred. For example, in the query “order sapper” we should still prefer the option “collector” rather than “welder”.
If you approach the task of correcting typos from a probabilistic point of view, it is quite natural to come to a model of a noisy channel :
- alphabet set ;
- set of all trailing lines over it;
- many lines that are correct words ;
- given distributions where .
Then the correction task is set as finding the correct word w for input s. Depending on the source of the error, measure it can be built in different ways, in our case it’s wise to try to estimate the probability of typos (let's call them elementary replacements) , where t, r are symbolic n-grams, and then evaluate as the probability of getting s from w by the most probable elementary replacements.
Let be - splitting the string x into n substrings (possibly zero). The Brill-Moore model involves the calculation of probability in the following way:
But we need to find :
By learning to evaluate P (w | s), we will also solve the problem of ranking options with the same Damerau-Levenshtein distance and will be able to take into account the context when correcting a typo.
Calculation
To calculate the probabilities of elementary substitutions, user queries will help us again: we will compose pairs of words (s, w) which
- close in Damerau-Levenshtein;
- one of the words is more common than the other N times.
For such pairs, we consider the optimal alignment according to Levenshtein:

We compose all possible partitions of s and w (we limited ourselves to lengths n = 2, 3): n → n, pr → rn, pro → rn, ro → po, m → ``, mm → m, etc. For each n-gram, we find
Calculation
Calculation directly takes : we need to sort through all possible partitions of w with all possible partitions of s. However, the dynamics on the prefix can give an answer for where n is the maximum length of elementary substitutions:
Here P is the probability of the corresponding row in the k-gram model. If you look closely, it is very similar to the Wagner-Fisher algorithm with Ukkonen clipping. At every step we get by enumerating all the fixes at provided and the choice of the most probable one.
Back to
So, we can calculate . Now we need to select several options w maximizing . More precisely, for the original request you must choose where maximum. Unfortunately, an honest choice of options did not fit into our response time requirements (and the project deadline was drawing to a close), so we decided to focus on the following approach:
- from the original query we get several options by changing the k last words:
- we correct the keyboard layout if the resulting term has a probability several times higher than the original one;
- we find words whose Damerau-Levenshtein distance does not exceed d;
- choose from them top-N options for ;
- send BeamSearch to the input along with the original request;
- when ranking the results we discount the obtained options on .
For Clause 1.2, we used the FB-Trie algorithm (forward and backward trie), based on fuzzy search in the forward and reverse prefix trees. This turned out to be faster than evaluating P (s | w) throughout the dictionary.
Query Statistics
With the construction of the language model, everything is simple: we collect statistics on user queries (how many times we made a request for a given phrase, how many users, how many registered users), we break down requests into n-grams and build burs. More complicated with the error model: at a minimum, a dictionary of the right words is needed to build it. As mentioned above, to select the training pairs, we used the assumption that such pairs should be close in Damerau-Levenshtein distance, and one should occur more often than the other several times.
But the data is still too noisy: xss injection attempts, incorrect layout, random text from the clipboard, experienced users with requests “programmer c not 1c”,
For example, what did you try to find by such a request? 

Therefore, to clear the source data, we excluded:
- low frequency terms;
- Containing query language operators
- obscene vocabulary.
They also corrected the keyboard layout, checked against words from the texts of vacancies and open dictionaries. Of course, it was not possible to fix everything, but such options are usually either completely cut off or located at the bottom of the list.
In prod
Right before project protection, they launched a service in production for internal testing, and after a couple of days - for 20% of users. In hh.ru, all changes that are significant to users go through a system of AB tests , which allows us not only to be sure of the significance and quality of the changes, but also to find errors .

The metric of the average number of searches from the sujest to the applicants has brightened up (increased from 0.959 to 1.1355), and the share of searches from the sujest of all search queries has increased from 12.78% to 15.04%. Unfortunately, the main product metrics have not grown, but users have definitely become more likely to use tips.
In the end
There was no room for a story about the School's processes, other tested models, the tools that we wrote for model comparisons, and meetings where we decided which features to develop in order to catch up with the intermediate demos. Look at the records of the past school , leave a request at https://school.hh.ru , complete interesting tasks and come to study. By the way, the service for checking tasks was also done by the graduates of the previous set.
What to read?
All Articles