Convert black and white images to ASCII graphics using non-negative matrix decomposition

In general, converting an image to ASCII graphics is a rather time-consuming task, but there are algorithms that automate this process. This article discusses the approach proposed by researchers Paul D. O'Grady and Scott T. Rickard in "Automatic ASCII Art Conversion of Binary Images Using Non-Negative Constraints . " The method described by them involves representing the image conversion process as an optimization problem and solving this problem using a non-negative matrix decomposition. Below is a description of the algorithm in question, as well as its implementation:

Algorithm description

The original image is divided into blocks of size where and - width and height of one character in pixels. If the width \ height of the image is not a multiple of the width \ height of the character, then the picture is cropped or supplemented with white areas of the desired size.









Each of blocks obtained after the partition is represented as a vector of length whose values ​​are the color intensities of the pixels in the image (values ​​from 0 to 255, where the white pixel corresponds to 0, and the black pixel corresponds to 255). The resulting vectors should be normalized using the norm :

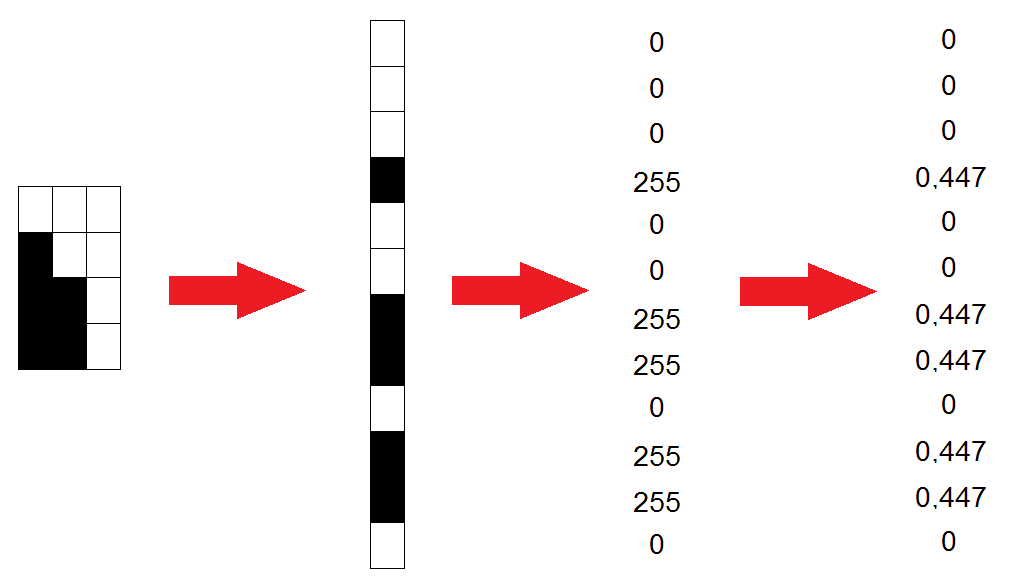
The normalized vectors are rewritten in the form of columns, thus forming a matrix the size .







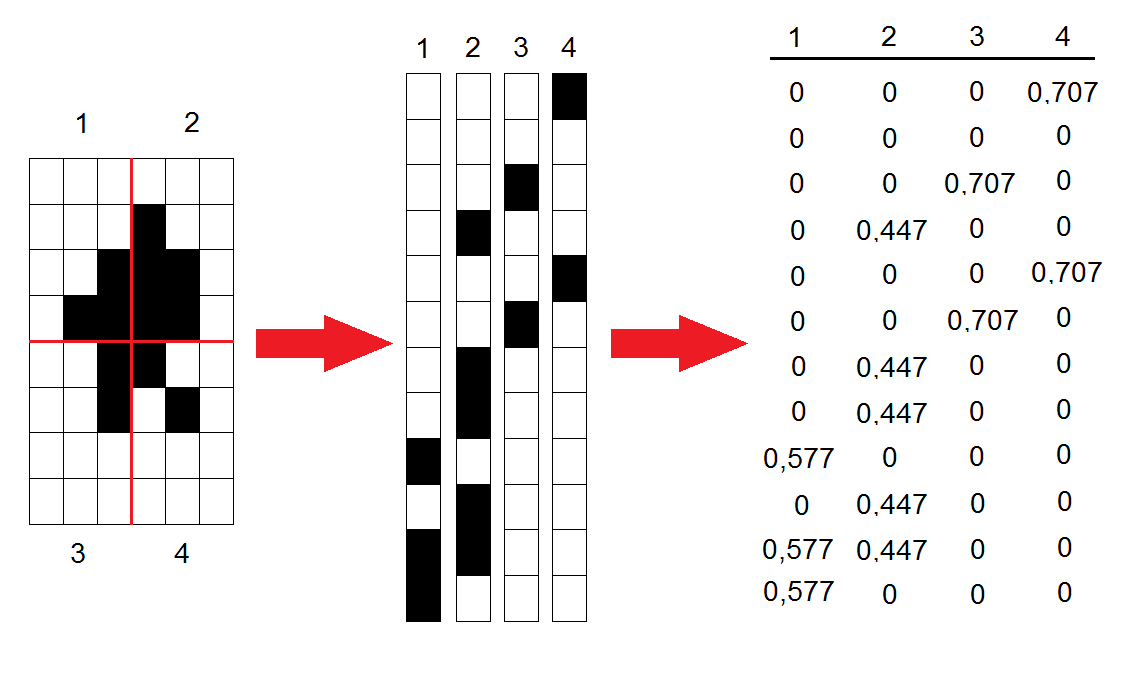
The resulting matrix need to be represented as a product of matrices and all elements of which are non-negative:

Matrix known in advance: it is constructed similarly to the matrix , but instead of sections of the original image, images of all symbols used in the generation of ASCII graphics are used. If the applicable kit includes characters then the matrix will have a size .

It remains only to choose a matrix in such a way as to minimize the value of some objective function characterizing the difference between and work . The following dependence is used as such a function:

This expression essentially combines several objective functions: when it is converted to the square of the Euclidean distance (Squared Euclidean Distance), when approaches the Kullback-Leibler Divergence distance, and when - to the distance of Itakura-Saito (Itakura-Saito Divergence).



Direct matrix selection produced as follows: initialized with random values ​​from 0 to 1, after which its values ​​are iteratively updated according to the following rule (the number of iterations is set in advance):

Each value corresponds to the degree of similarity character from the set with -th section of the image.









So, to determine which character should be replaced section, it is enough to find the maximum value in th column of the matrix . The line number in which this value is located will be the number of the character to search for in the set. You can also enter some threshold value. , and if the found maximum value is less than this threshold, then the image section is replaced by a space. Using a space can have a positive effect on the appearance of the resulting image compared to using a symbol with a low degree of similarity.

Implementation

The algorithm is implemented in C #. ASCII graphics are generated using 95 characters (from 0x20 to 0x7E) with a size of 11x23 pixels; The font used is Courier. Below is the source code for the function to convert the original image to ASCII graphics:

public static char[,] ConvertImage( Bitmap image, double beta, double threshold, ushort iterationsCount, ushort threadsNumber, Action<int> ProgressUpdated) { int charNumHor = (int)Math.Round((double)image.Width / glyphWidth); int charNumVert = (int)Math.Round((double)image.Height / glyphHeight); int totalCharactersNumber = charNumVert * charNumHor; int glyphSetSize = wNorm.ColumnCount; Matrix<double> v = SplitImage(image, charNumVert, charNumHor); Matrix<double> h = Matrix<double>.Build.Random( glyphSetSize, totalCharactersNumber, new ContinuousUniform()); int progress = 0; ushort step = (ushort)(iterationsCount / 10); for (ushort i = 0; i < iterationsCount; i++) { UpdateH(v, wNorm, h, beta, threadsNumber); if((i + 1) % step == 0) { progress += 10; if(progress < 100) { ProgressUpdated(progress); } } } var result = GetAsciiRepresentation(h, charNumVert, charNumHor, threshold); ProgressUpdated(100); return result; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Consider each step individually:



1) We calculate how many characters can fit in the width and height of the image:

 int charNumHor = (int)Math.Round((double)image.Width / glyphWidth); int charNumVert = (int)Math.Round((double)image.Height / glyphHeight);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Using the calculated values, we divide the original image into blocks of the required size. For each block, we write the values ​​of the pixel color intensity in the corresponding column of the matrix (if necessary, we expand the original image by adding zero values ​​corresponding to white pixels to the matrix), after which we normalize all the columns:

 private static Matrix<double> SplitImage( Bitmap image, int charNumVert, int charNumHor) { Matrix<double> result = Matrix<double>.Build.Dense( glyphHeight * glyphWidth, charNumHor * charNumVert); for (int y = 0; y < charNumVert; y++) { for (int x = 0; x < charNumHor; x++) { for (int j = 0; j < glyphHeight; j++) { for (int i = 0; i < glyphWidth; i++) { byte color = 0; if ((x * glyphWidth + i < image.Width) && (y * glyphHeight + j < image.Height)) { color = (byte)(255 - image.GetPixel( x * glyphWidth + i, y * glyphHeight + j).R); } result[glyphWidth * j + i, charNumHor * y + x] = color; } } } } result = result.NormalizeColumns(2.0); return result; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

2) Fill the matrix random values ​​from 0 to 1:

 Matrix<double> h = Matrix<double>.Build.Random( glyphSetSize, totalCharactersNumber, new ContinuousUniform());
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

We apply the update rule a specified number of times to its elements:

 for (ushort i = 0; i < iterationsCount; i++) { UpdateH(v, wNorm, h, beta, threadsNumber); if((i + 1) % step == 0) { progress += 10; if(progress < 100) { ProgressUpdated(progress); } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Directly updating the matrix elements is implemented as follows (unfortunately, the problems associated with division by zero are solved with the help of some crutches):

 private static void UpdateH( Matrix<double> v, Matrix<double> w, Matrix<double> h, double beta, ushort threadsNumber) { const double epsilon = 1e-6; Matrix<double> vApprox = w.Multiply(h); Parallel.For( 0, h.RowCount, new ParallelOptions() { MaxDegreeOfParallelism = threadsNumber }, j => { for (int k = 0; k < h.ColumnCount; k++) { double numerator = 0.0; double denominator = 0.0; for (int i = 0; i < w.RowCount; i++) { if (Math.Abs(vApprox[i, k]) > epsilon) { numerator += w[i, j] * v[i, k] / Math.Pow(vApprox[i, k], 2.0 - beta); denominator += w[i, j] * Math.Pow(vApprox[i, k], beta - 1.0); } else { numerator += w[i, j] * v[i, k]; if (beta - 1.0 > 0.0) { denominator += w[i, j] * Math.Pow(vApprox[i, k], beta - 1.0); } else { denominator += w[i, j]; } } } if (Math.Abs(denominator) > epsilon) { h[j, k] = h[j, k] * numerator / denominator; } else { h[j, k] = h[j, k] * numerator; } } }); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

3) The last step is to choose a suitable symbol for each image section by finding the maximum values ​​in the matrix columns :

 private static char[,] GetAsciiRepresentation( Matrix<double> h, int charNumVert, int charNumHor, double threshold) { char[,] result = new char[charNumVert, charNumHor]; for (int j = 0; j < h.ColumnCount; j++) { double max = 0.0; int maxIndex = 0; for (int i = 0; i < h.RowCount; i++) { if (max < h[i, j]) { max = h[i, j]; maxIndex = i; } } result[j / charNumHor, j % charNumHor] = (max >= threshold) ? (char)(firstGlyphCode + maxIndex) : ' '; } return result; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

The resulting image is written to the html file. The full source code of the program can be found here .

Examples of generated images

Below are examples of images generated at various parameter values and the number of iterations. The original image was 407x500 pixels in size, respectively, the resulting images were 37x22 characters in size.

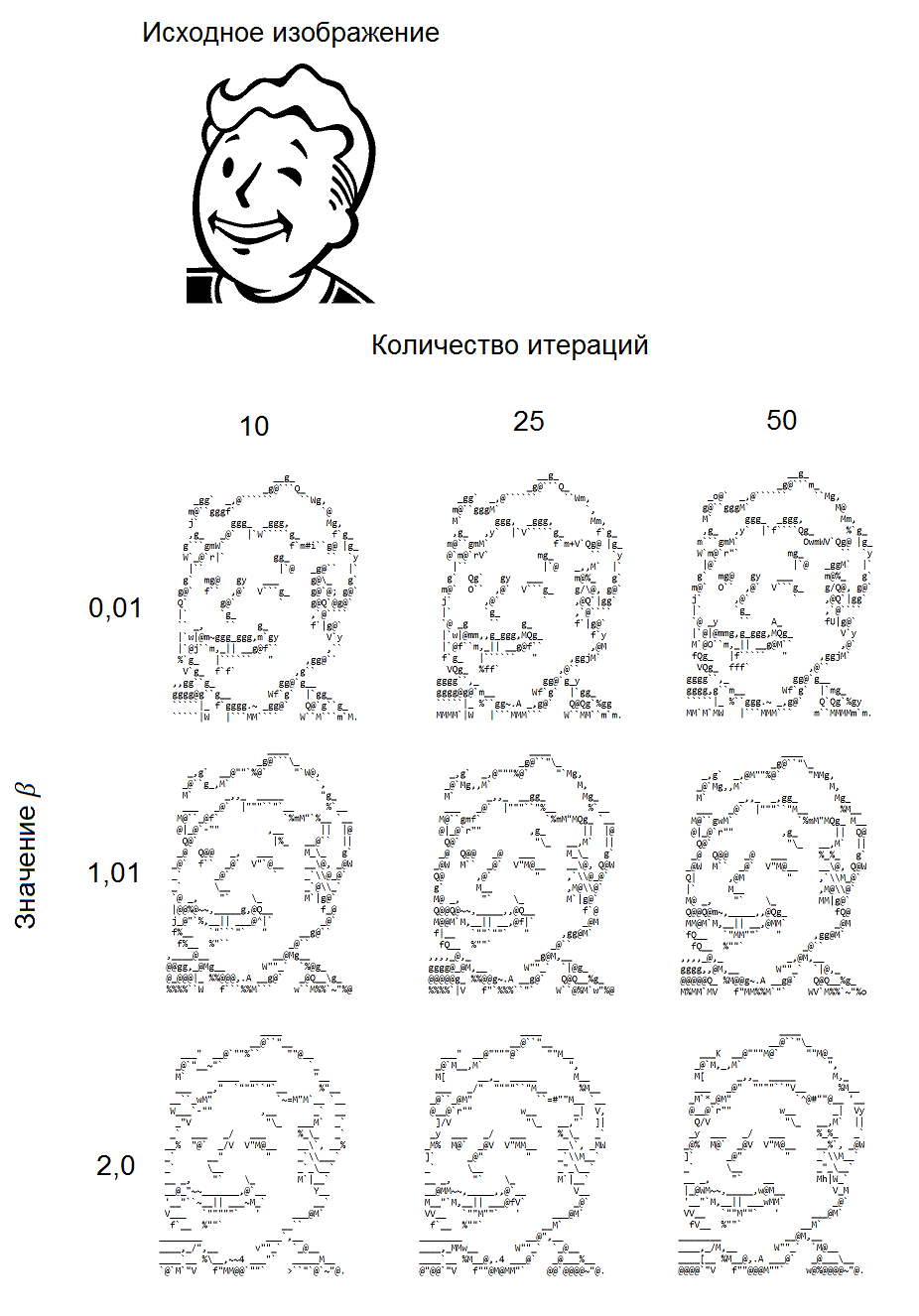
Conclusion

In the considered algorithm, the following disadvantages can be distinguished:

1. Long image processing: depending on the size of the image and the number of iterations, its processing can take from several tens of seconds to several tens of minutes.
2. Poor quality processing of detailed images. For example, an attempt to convert an image of a human face yields the following result:
   
   
   
   
   
   
   
   
   
   

At the same time, reducing the number of parts by increasing the brightness and contrast of the image can significantly improve the appearance of the resulting image:









In general, despite these shortcomings, we can conclude that the algorithm gives satisfactory results.