New Year, New Records: 50th Mersenne Prime Number Found
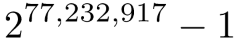
Raleigh, North Carolina, January 3, 2018 — The Great Internet Mersenne Prime Search organization (GIMPS, a large-scale Internet project to search for Mersenne primes) discovered the largest known prime number of 2,772,32917 -1, consisting of 23,249,425 digits . Jonathan Pace's computer volunteer calculated it on December 26, 2017. Jonathan is one of thousands of volunteers using the free software GIMPS .
The new prime number, also known as M77232917, is calculated by multiplying 77 232 917 twos and subtracting one. It is about one million more than the previous record prime number , in a special class of extremely rare prime numbers, known as the Mersenne numbers. This is just the 50th open prime number of Mersenne; the calculation of each subsequent becomes more difficult. Mersenne prime numbers are named for the French monk Marina Mersenne , who studied these numbers more than 350 years ago. Founded in 1996, GIMPS discovered the last 16 Mersenne primes. Volunteers download a free program to search for these simple numbers and have a chance to win a cash prize if they are lucky to find a new number.
Professor Chris Caldwell has a reputable website dedicated to the largest known simple numbers with a remarkable history of Mersenne prime numbers .
The simplicity check took six days of non-stop computing on a PC with an Intel i5-6600 processor. To prove that there are no errors in the detection of primes, the new prime number is checked in four different programs on four different hardware configurations.
- Aaron Blosser checked it using Prime95 on an Intel Xeon server in 37 hours.
- David Stanfill checked the gpuOwL number on the AMD RX Vega 64 video processor in 34 hours.
- Andreas Hoglund tested a prime number using CUDALucas on the NVidia Titan Black GPU video processor for 73 hours.
- Ernst Meyer checked the number in his own Mlucas program on a 32-core Xeon server in 82 hours. Andreas Hoglund confirmed his results by running Mlucas on an Amazon AWS virtual machine for 65 hours.
Jonathan Pace is a 51-year-old electrical engineer living in Germantown, Tennessee. His perseverance was finally rewarded - Jonathan had been hunting for large prime numbers with GIMPS for over 14 years. For his discovery, he received a research award of $ 3,000 from GIMPS.
Prime95 client software developed by GIMPS founder George Waltman. Scott Kurovski has written PrimeNet system software that coordinates GIMPS computers. Aaron Blosser now works as a system administrator and, if necessary, performs updates and maintenance of PrimeNet. Volunteers have a chance to get a reward of $ 3,000 or $ 50,000 if their computer opens a new Mersenne prime number. The next major goal of GIMPS is to win a $ 150,000 award established by the Electronic Frontier Foundation, which will be awarded for finding a prime number with 100,000,000 bits.
We are grateful for finding this prime number not only to Jonathan Pace, who ran Prime95 software on his computer: Waltman for written software, Kurovsky and Blosseur for their work with the Primenet server, as well as thousands of GIMPS volunteers who sifted millions of numbers. In gratitude to all these people, this discovery is officially attributed to “J. Pace, J. Waltman, S. Kurovsky, A. Blossseur and colleagues.
About Great Internet Mersenne Prime Search
The Great Internet Mersenne Prime Search (GIMPS) was formed in January 1996 by George Waltman to find new world records of Mersenne's prime numbers. In 1997, Scott Kurovsky made it possible for GIMPS to use the power of thousands of ordinary computers to search for these “needles in a haystack”. Most GIMPS members joined the organization for the exciting opportunity to discover a record, rare and historic new prime Mersenne number. The search for the following Mersenne prime numbers is already ongoing There may be fewer, but so far unlisted simple ones, and almost certainly there are more to be discovered. Anyone with a powerful enough computer can join GIMPS and become a hunter for large prime numbers with the ability to get a cash reward for their discovery. All necessary software can be downloaded for free at www.mersenne.org/download/ . GIMPS is formed as Mersenne Research, Inc., a non-profit, scientific, charitable organization 501 (c) (3). Read more about this at www.mersenneforum.org and www.mersenne.org ; donations are also accepted.
More information on Mersenne primes
Prime numbers have long admired both amateurs and professionals of mathematics. An integer greater than one is called a prime number if its only divisors are one and it itself. The first prime numbers are 2, 3, 5, 7, 11, etc. For example, the number 10 is not prime, because it is divisible by 2 and 5. A Mersenne prime number is a prime number that has the form 2 P - 1. The first Mersenne prime numbers are 3, 7, 31, and 127, corresponding to P = 2, 3 , 5 and 7. So far, 50 Mersenne prime numbers are known.
Mersenne prime numbers have been in the spotlight of number theory since when Euclid first reviewed them about 350 BC. The man named after these numbers, a French monk Marin Mersenne (1588-1648), created the famous hypothesis of what values of P can be used to obtain a prime number. To confirm this hypothesis, it took 300 years and several important discoveries.
Today there are few practical applications of this prime number, which makes some wonder: “Why look for such large prime numbers at all”? Similar doubts existed several decades ago, until finally important cryptographic algorithms based on prime numbers were developed. Another seven good reasons for finding large prime numbers are outlined here .
Previous discoveries of the Mersenne primes in the framework of the GIMPS were made by participants from different countries.
Chronology
In January 2016, Curtis Cooper and his colleagues discovered the 49th known Mersenne prime number in the United States.
In January 2013, the same Curtis Cooper and colleagues found the 48th known Mersenne prime number .
In April 2009, Odd Magnar Strindmo and his colleagues discovered the 47th known Mersenne prime number in Norway.
In September 2008, Hans-Michael Elvenich and his colleagues discovered the 46th known Mersenne prime number in Germany.
In August 2008, Edson Smith and his colleagues found the 45th in the United States.
In September 2006, Curtis Cooper, Stephen Boone and colleagues discovered the 44th prime Mersenne number .
In December 2005, Curtis Cooper, Stephen Boone and colleagues found the 43rd number of Mersenne .
In February 2005, Dr. Martin Novak and his colleagues calculated the 42nd known Mersenne prime number in Germany.
In May 2004, Josh Findlay and his colleagues discovered the 41st prime Mersenne .
In November 2003, Michael Schäfer and his colleagues found the 40th known Mersenn prime number in the United States.
In November 2001, Michael Cameron and colleagues calculated the 39th Mersenne prime number in Canada.
In June 1999, Nayan Hajravalla and his colleagues discovered the 38th prime Mersenne number in the United States.
In January 1998, Roland Clarkson and his colleagues discovered the 37th prime Mersenne number in the United States.
In August 1997, Gordon Spence and his colleagues found the 36th Mersenne prime number in the United States.
In November 1996, Joël Armengo and his colleagues discovered the 35th famous Mersenne prime number in France.
In January 2013, the same Curtis Cooper and colleagues found the 48th known Mersenne prime number .
In April 2009, Odd Magnar Strindmo and his colleagues discovered the 47th known Mersenne prime number in Norway.
In September 2008, Hans-Michael Elvenich and his colleagues discovered the 46th known Mersenne prime number in Germany.
In August 2008, Edson Smith and his colleagues found the 45th in the United States.
In September 2006, Curtis Cooper, Stephen Boone and colleagues discovered the 44th prime Mersenne number .
In December 2005, Curtis Cooper, Stephen Boone and colleagues found the 43rd number of Mersenne .
In February 2005, Dr. Martin Novak and his colleagues calculated the 42nd known Mersenne prime number in Germany.
In May 2004, Josh Findlay and his colleagues discovered the 41st prime Mersenne .
In November 2003, Michael Schäfer and his colleagues found the 40th known Mersenn prime number in the United States.
In November 2001, Michael Cameron and colleagues calculated the 39th Mersenne prime number in Canada.
In June 1999, Nayan Hajravalla and his colleagues discovered the 38th prime Mersenne number in the United States.
In January 1998, Roland Clarkson and his colleagues discovered the 37th prime Mersenne number in the United States.
In August 1997, Gordon Spence and his colleagues found the 36th Mersenne prime number in the United States.
In November 1996, Joël Armengo and his colleagues discovered the 35th famous Mersenne prime number in France.
Euclid proved that every Mersenne prime generates a perfect number. A perfect number is a number whose sum of its own divisors is equal to the number itself. The smallest perfect number is 6 = 1 + 2 + 3, the second is 28 = 1 + 2 + 4 + 7 + 14. Euler (1707-1783) proved that all even perfect numbers are the result of Mersenne's prime numbers. The last perfect open number is 2,77232916 x ( 2,77232917 -1). This number has more than 46 million digits ! It is still unknown if odd perfect numbers exist.
The arithmetic algorithms underlying the GIMPS project have a unique history. Programs that find the last large prime numbers of Mersenne are based on a special algorithm. In the early 1990s, the late Richard Crandall , an eminent scientist at Apple, discovered ways to double the speed of convolutions — very large multiplication operations. This method is applicable not only to the search for primes, but also to other aspects of the calculations. In the process of working on this project, he also patented the Fast Elliptic Encryption encryption system, which is now owned by Apple Computer. It uses Mersenne prime numbers to quickly encrypt and decrypt messages. George Waltman implemented the Crandall algorithm in assembly language, thus creating a program to search for primes with unprecedented efficiency. This work led to the creation of a successful GIMPS project.
School teachers use GIMPS to interest their students in mathematics. Students running software on their computers contribute to mathematical research.
Supplement from the post of John D. Cook.
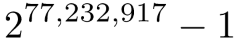
This number consists of 23,249,425 digits when written in decimal form.
In binary form, 2 p - 1 is a sequence of p ones. For example, 31 = 2 5 - 1 equals 11111 in binary form. That is, in binary form, a new record prime number is a string of 77,232,917 units.
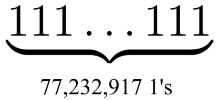
A binary number can be converted to hexadecimal (base 16), starting at the right end and converting blocks of four bits to hexadecimal numbers. For example, to convert 101101111 to HEX, we divide the number into three blocks: 1, 0110, and 1111. These blocks are converted to 1, 6, and F, that is, the binary 101101111 corresponds to hexadecimal 16F.
Further, 77 232 917 = 19 308 229 * 4 + 1, that is, we divide our line of 77 232 917 units into groups of four digits, receiving one remaining bit, followed by 19 308 229 groups of four digits. This means that in hexadecimal notation, a new record prime number has the form 1FFF ... FFF - the unit, followed by 19 308 229 F.
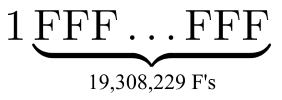
The new record is the 50th prime Mersenn number. Mersenne's prime number is a prime number one less than the power of two, i.e. has the form 2 p - 1. It turned out that for simplicity 2 p - 1 the number p should also be simple. In the case of a new record 77,232,917 is simple.
It is not known whether there is an infinite number of Mersenne primes. But now we know that there are at least 50 of them.
All the latest records of prime numbers were Mersenne numbers, because there is an algorithm for checking whether a number of the form 2 p - 1 is simple ( Luke-Lemer test ).
All Articles