How the Higgs field works: 2) why the Higgs field is nonzero on average
How the Higgs field works:
How is it that the Higgs field in nature has a mean value that is not zero, while for others (apparently, elementary) fields of nature, known to us, it is zero? [A very small font: other fields, with the exception of the gravitational field of the lowest level, are called metric, this allows us to determine the existence of space and time].
First, fermion fields cannot have a large constant nonzero value in nature. This is due to the difference between fermions and bosons. Bosons can be non-zero on average, but fermions cannot. So you can forget about electrons (and their cousins muons and tau), about neutrinos and quarks. Fine print: fermions can pair with each other or with antifermions and make composite bosons, which can be non-zero on average. This is so for the upper and lower quarks and their antiquarks, and for electrons in a superconductor. But it is a long story, and it does not concern ours directly.
What about photon fields, gluons, W and Z? These are all bosons. In principle, these fields could have a constant non-zero average value over the Universe. But experiments, not theory, say that it is not. A sufficiently large nonzero value of the electric field would lead to the appearance of various effects, which we do not observe. The most important of these would be the violation of rotational invariance on a large scale. The electric field is a vector (spin-1), it points in a certain direction, so if it is non-zero, then the direction in which this value points should be different from all others. (Fig. 1, lower left).
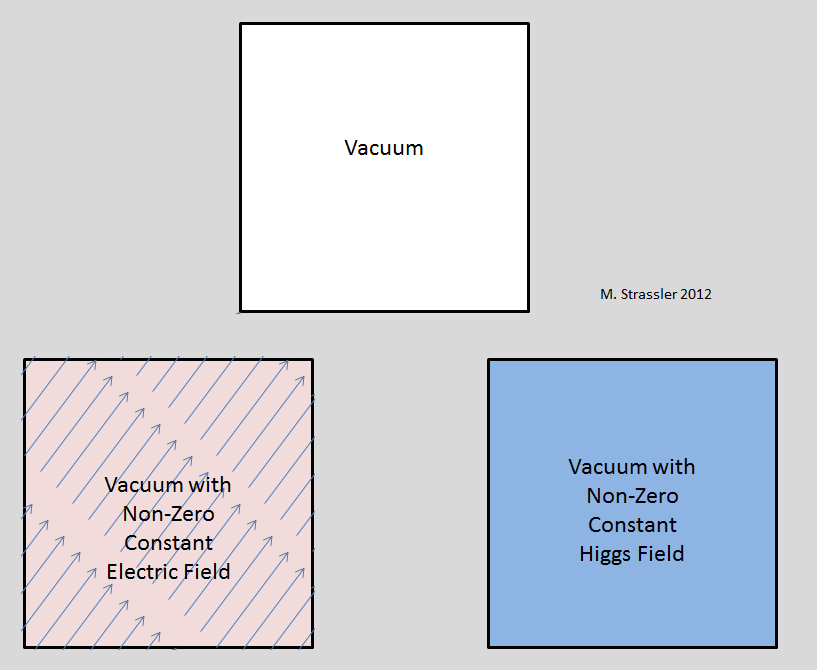
Fig. one
The Higgs field is scalar (spin 0), it does not indicate anywhere. Among other scalar fields (non-elementary and non-relativistic) we can give examples of the air density field, the pressure field inside the Earth, the ocean temperature. At every point in space and time, density or pressure or temperature is just a number, and the electric field is the number and direction. So if the Higgs field has a nonzero value, no preferred direction arises - fig. 1, lower right. What is more strange (since it is relativistic), the Higgs field does not generate any preferred frame of reference. For air density, there is a preferred frame of reference, since you either rest at rest with respect to the air, or move through it. But for the Higgs field it is not; all observers are resting relative to him. Therefore, the success of Einstein's STR, describing all phenomena, does not contradict the presence of a relativistic scalar field of nonzero value, such as the Higgs field. In short, in the presence of a non-zero Higgs field, the vacuum behaves exactly as it would behave at H = 0; its presence can be detected only through the effect on the masses of the particles (or through something more cardinal, for example, the use of the LHC to create the Higgs particles).
The easiest way for the Higgs field would be to maintain a nonzero value throughout the Universe if it had a nonzero equilibrium value H 0 participating in its class 1 motion equation:
(It should be class 1, not class 0, for reasons that will become clear to us after discussing the Higgs particle). In fact, the situation is a bit more complicated. The correct equation will look like this:
Where a and b are constants (their squares are positive! Note the plus sign in front of a 2 H, and compare it with the minus in the previous equation), which we will learn about later. This can be rewritten as:
If H (x, t) is a constant in space and time, then dH / dt = dH / dx = 0, therefore
(when H (x, t) is a constant in x and t), and it has solutions (for now, we simplify everything a lot):
1. H = 0
2. H = + a / b
3. H = - a / b
In other words, there are three equilibrium positions, not one. Small print: I greatly simplify here, but without prejudice to the meaning.
This is not immediately clear, but the solution H = 0 is unstable. The situation is similar to the equation of motion of a ball in a bowl of such a shape as shown in fig. 2 - similar to the bottom of a wine bottle. He also has three equilibrium positions, one at 0 and two at ± x 0 . But obviously the position at 0 is unstable - any push will force the red ball to roll away far from x = 0, a fundamental change in the situation. Conversely, the equilibrium in x = x 0 is stable, since any push will cause the green ball to oscillate with a small amplitude around the point x = x 0 - not such a drastic change. The same will be true for a light green ball on x = -x 0 . Similarly, although H = 0 will be a solution to the Higgs field, the history of our Universe has turned out to be quite complicated to guarantee how to kick the Higgs field, so it could not remain in this position. Instead, the Higgs field turned out to be in a solution with a nonzero value and in a stable situation.

For decades, thanks to a combination of experiments and theory, we knew that the value of the Higgs field (which is traditionally called “v”) is 246 GeV. This gives us an idea of those constants a and b:
a = vb = (246 GeV) b
So you can define a through b, and you can rewrite the Higgs motion equation:
But this does not give us an idea about b itself. In the next article we will learn more about it.
Now, although I prepared everything so that H can be equal to v or –v, it does not matter whether the value of the Higgs field is positive or negative (in fact, there are even more possibilities, see below); the world will turn out exactly the same with the same physics, since nothing depends on the sign of H. This does not become immediately apparent, but it is; one clue - wherever you find H in the equations I describe or in the description of how the Higgs field works, H 2 appears everywhere, not just H - and H 2 does not depend on whether H = v or H = -v . [Small print: in fact, H is a complex field, with a real and imaginary part, therefore H can be equal to v multiplied by any complex number z, for which | z | = 1; and in fact in the equations H * H = | H | 2 , but it does not depend on z. And even this is not all! But that's enough for today.]
If you find a way (say, pushing protons at each other at the Large Hadron Collider) to somehow push or disturb the Higgs field, it will oscillate to and fro — that is, waves will appear in it
Where A is the wave amplitude, ν and λ are the frequency and wavelength, and the relationship between ν and λ depends on the exact form of the equation of motion, in particular, on b and v. Since the Higgs field is quantum, these waves will amplify the amplitude of these waves, and we call the quantum of these waves a Higgs particle. Next time we will look at the properties of these particles.
- main idea
- Why the Higgs field is nonzero on average
- How does the Higgs particle appear
- Why the Higgs Field is Necessary
How is it that the Higgs field in nature has a mean value that is not zero, while for others (apparently, elementary) fields of nature, known to us, it is zero? [A very small font: other fields, with the exception of the gravitational field of the lowest level, are called metric, this allows us to determine the existence of space and time].
First, fermion fields cannot have a large constant nonzero value in nature. This is due to the difference between fermions and bosons. Bosons can be non-zero on average, but fermions cannot. So you can forget about electrons (and their cousins muons and tau), about neutrinos and quarks. Fine print: fermions can pair with each other or with antifermions and make composite bosons, which can be non-zero on average. This is so for the upper and lower quarks and their antiquarks, and for electrons in a superconductor. But it is a long story, and it does not concern ours directly.
What about photon fields, gluons, W and Z? These are all bosons. In principle, these fields could have a constant non-zero average value over the Universe. But experiments, not theory, say that it is not. A sufficiently large nonzero value of the electric field would lead to the appearance of various effects, which we do not observe. The most important of these would be the violation of rotational invariance on a large scale. The electric field is a vector (spin-1), it points in a certain direction, so if it is non-zero, then the direction in which this value points should be different from all others. (Fig. 1, lower left).

Fig. one
The Higgs field is scalar (spin 0), it does not indicate anywhere. Among other scalar fields (non-elementary and non-relativistic) we can give examples of the air density field, the pressure field inside the Earth, the ocean temperature. At every point in space and time, density or pressure or temperature is just a number, and the electric field is the number and direction. So if the Higgs field has a nonzero value, no preferred direction arises - fig. 1, lower right. What is more strange (since it is relativistic), the Higgs field does not generate any preferred frame of reference. For air density, there is a preferred frame of reference, since you either rest at rest with respect to the air, or move through it. But for the Higgs field it is not; all observers are resting relative to him. Therefore, the success of Einstein's STR, describing all phenomena, does not contradict the presence of a relativistic scalar field of nonzero value, such as the Higgs field. In short, in the presence of a non-zero Higgs field, the vacuum behaves exactly as it would behave at H = 0; its presence can be detected only through the effect on the masses of the particles (or through something more cardinal, for example, the use of the LHC to create the Higgs particles).
The easiest way for the Higgs field would be to maintain a nonzero value throughout the Universe if it had a nonzero equilibrium value H 0 participating in its class 1 motion equation:
d2H/dt2−c2d2H/dx2=−(2 pi numin)2(H−H0)
(It should be class 1, not class 0, for reasons that will become clear to us after discussing the Higgs particle). In fact, the situation is a bit more complicated. The correct equation will look like this:
d2H/dt2−c2d2H/dx2=a2H−b2H3
Where a and b are constants (their squares are positive! Note the plus sign in front of a 2 H, and compare it with the minus in the previous equation), which we will learn about later. This can be rewritten as:
d2H/dt2−c2d2H/dx2=−b2H(H2−[a/b]2)
If H (x, t) is a constant in space and time, then dH / dt = dH / dx = 0, therefore
0=−b2H(H2−[a/b]2)
(when H (x, t) is a constant in x and t), and it has solutions (for now, we simplify everything a lot):
1. H = 0
2. H = + a / b
3. H = - a / b
In other words, there are three equilibrium positions, not one. Small print: I greatly simplify here, but without prejudice to the meaning.
This is not immediately clear, but the solution H = 0 is unstable. The situation is similar to the equation of motion of a ball in a bowl of such a shape as shown in fig. 2 - similar to the bottom of a wine bottle. He also has three equilibrium positions, one at 0 and two at ± x 0 . But obviously the position at 0 is unstable - any push will force the red ball to roll away far from x = 0, a fundamental change in the situation. Conversely, the equilibrium in x = x 0 is stable, since any push will cause the green ball to oscillate with a small amplitude around the point x = x 0 - not such a drastic change. The same will be true for a light green ball on x = -x 0 . Similarly, although H = 0 will be a solution to the Higgs field, the history of our Universe has turned out to be quite complicated to guarantee how to kick the Higgs field, so it could not remain in this position. Instead, the Higgs field turned out to be in a solution with a nonzero value and in a stable situation.

For decades, thanks to a combination of experiments and theory, we knew that the value of the Higgs field (which is traditionally called “v”) is 246 GeV. This gives us an idea of those constants a and b:
a = vb = (246 GeV) b
So you can define a through b, and you can rewrite the Higgs motion equation:
d2H/dt2−c2d2H/dx2=−b2H(H2−v2)
But this does not give us an idea about b itself. In the next article we will learn more about it.
Now, although I prepared everything so that H can be equal to v or –v, it does not matter whether the value of the Higgs field is positive or negative (in fact, there are even more possibilities, see below); the world will turn out exactly the same with the same physics, since nothing depends on the sign of H. This does not become immediately apparent, but it is; one clue - wherever you find H in the equations I describe or in the description of how the Higgs field works, H 2 appears everywhere, not just H - and H 2 does not depend on whether H = v or H = -v . [Small print: in fact, H is a complex field, with a real and imaginary part, therefore H can be equal to v multiplied by any complex number z, for which | z | = 1; and in fact in the equations H * H = | H | 2 , but it does not depend on z. And even this is not all! But that's enough for today.]
If you find a way (say, pushing protons at each other at the Large Hadron Collider) to somehow push or disturb the Higgs field, it will oscillate to and fro — that is, waves will appear in it
H=v+Acos[2 pi( nut−x/ lambda)]
Where A is the wave amplitude, ν and λ are the frequency and wavelength, and the relationship between ν and λ depends on the exact form of the equation of motion, in particular, on b and v. Since the Higgs field is quantum, these waves will amplify the amplitude of these waves, and we call the quantum of these waves a Higgs particle. Next time we will look at the properties of these particles.
All Articles