Ask Ethan: What is so frightening about quantum entanglement?

By creating two entangled photons in the existing system, and then dividing them over a long distance, we can obtain information about the state of one of them by measuring the state of the other.



Quantum physics is full of mysteries, notorious for contradicting our intuition. The particles seem to know whether you are looking at them or not, and exhibit different behaviors, depending on whether you are watching them or not, passing through a double slit. Measuring one value, say, the position of a particle, creates its inherent uncertainty in the complementary value, for example, impulse. And if you measure its spin in the vertical direction, then destroy the information about the spin in the horizontal direction. But the most “frightening” of all quantum phenomena will be quantum entanglement, when one particle seems to instantly “find out” whether a partner entangled with it was measured, even if it was done at the other end of the Universe. This week we’ll look at a reader’s question, intrigued by why this is generally considered a mystery.

From the point of view of photons, they traveled a zero distance in zero time. So what's intimidating? Until one of them is measured, they are in the same place and at the same time (if you believe them), so it’s not a mystery that they coordinate their states.

Reasonable reasoning: slowing down time for fast moving particles means that they can coordinate their states at any speed. But this riddle is not so easy to solve.





The scheme of the third Aspe experiment to test quantum nonlocality. Entangled photons from the source are sent to two switches that direct them to the polarizing sensors. Switches very quickly switch their states, changing detector settings during the flight of photons.



To begin with, let's look at the question of entanglement. The experiment is usually carried out with photons: you transmit one quantum of light through a special material (a scattering crystal) that splits it into two photons. These photons will be entangled in a certain sense, that is, if one has a spin, an internal angular momentum, +1, then the other will have -1. But which one, we do not know. You can even do experiments in which, after considering a large number of photons, the difference between

• statistical results in the case of spin +1,

• statistical results in the case of spin -1,

• and statistical results if the spin remains undefined.



It is very difficult to visualize these results, but in quantum mechanics there is an excellent analogy: the passage of a particle through a double slit.





If you pass electrons, photons or any other particles through a double slit, a picture of interference arises. But this happens only if you do not check what gap they go through!



If you pass a particle through a double slit - that is, a screen with two narrow slits that are very close to each other - and it passes through them, instead of being delayed by the screen, you can easily determine where it will be on the other side. If you launch multiple particles one by one through a double potion, you will find that the particles that pass through the slits form an interference pattern. In other words, each particle behaves differently, as if it had passed through one or the other slit; she behaves as if she went through both slots at once, interfered with herself in the manner of a wave, and continued moving.



But this picture, which demonstrates the strange quantum-mechanical nature of all particles of the Universe, appears only if you do not determine which slit a particle passes through.





If you determine which slit a particle goes through, leaving the rest of the experiment unchanged, you don’t get an interference pattern at all.



If you instead measure a particle in a passage through one of the slots — this can be done through the installation of a counter — you will not get an interference pattern. You will get a bunch of particles, corresponding to passing through slot 1, and a pile for slot 2.





Wave pattern of electrons passing through a double slit one by one. If you measure the gap through which an electron has passed, you are destroying the quantum interference pattern. Note that to create such a picture requires more than one electron.



In other words, by taking a measurement that determines the path chosen by a particle, you change the result of this choice! For one particle, you can only determine the probability of passing through slot 1, slot 2, or interference with itself. To discover the real state of your experiment, you need more statistics.





Bell's quantum mechanical test for particles with half-integer spin



Let us return to the entangled photons. Or even to any tangled particles. You create two entangled particles, in which you know the total sum of their properties, but not the properties of each of them. The simplest example would be a spin — for two photons it will turn out to be either (+1 and -1) or (-1 and +1), for two electrons - (+ ½ and -½) or (-½ and + ½) - and you do not know which of them will have a spin, until you measure. Instead of slots, you can send them through a polarizer. And as soon as you measure one, you determine the other. In other words, you know it instantly.





A quantum erase experiment in which two entangled particles are separated and measured. Any actions with one of the particles at the destination do not affect the other.



"Frightening" is the fact that in physics nothing else happens instantly. The highest transmission speed of any signal will be equal to c, the speed of light in a vacuum. But these two entangled particles can be divided into meters, kilometers, astronomical units or light years, and the measurement of one of them instantly determines the state of the other. It does not matter whether entangled particles move at the speed of light or not, whether they have mass or not, whether they have much energy, and whether you isolate them from each other so that they do not send photons to each other. There are no loopholes that allow the speed of interaction in any reference system to somehow compensate for this. In the late 1990s, experiments with the separation and simultaneous measurement of these particles determined that if any information is transmitted between them, then it moves faster than the speed of light 10,000 times.





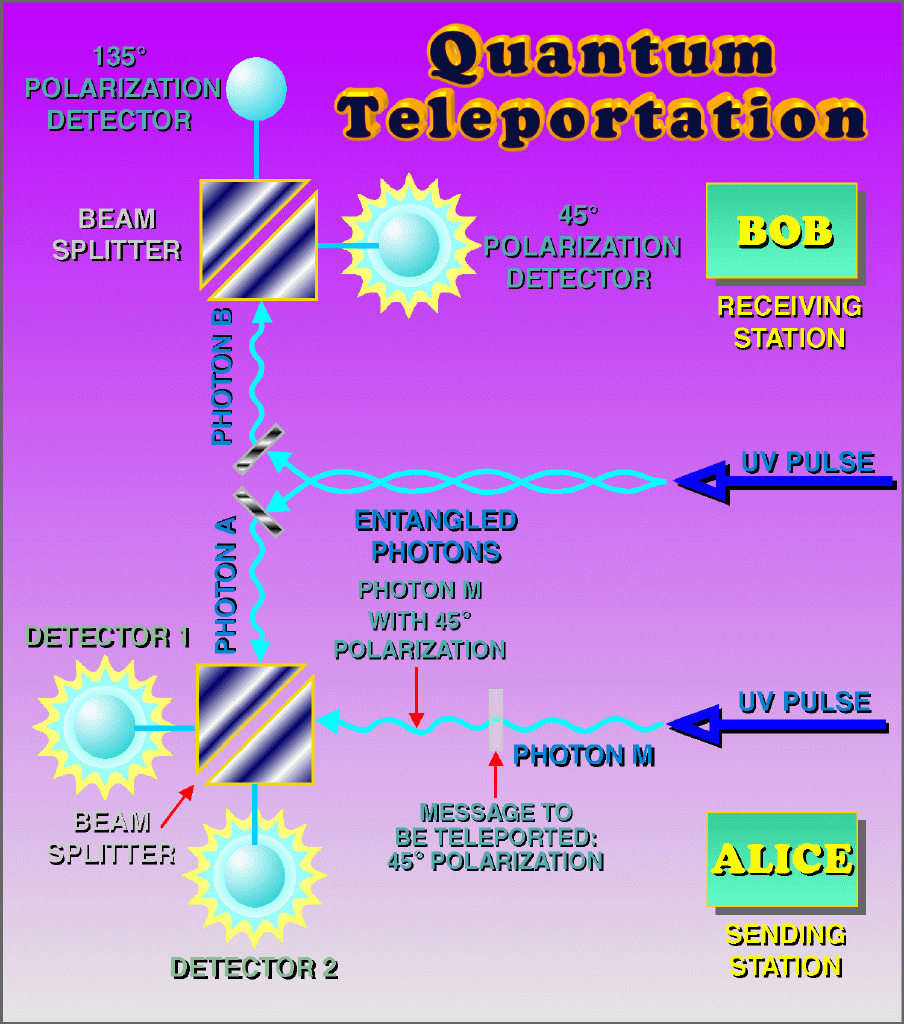
Quantum teleportation, which is often confused with traveling faster than light. In reality, information faster than the speed of light is not transmitted.



But this can not be! In reality, no information is transmitted. You cannot measure a particle in one place and use it to transfer something to a particle located very far away. Many ingenious schemes were designed, designed to transmit information faster than light using this property, but in 1993 they proved that this mechanism would not allow the transmission of information. There is a simple explanation for this:



• If you measure “the state of a particle I have,” you will recognize the state of another particle, but you cannot do anything with this information until either you get to another particle, or it gets to us, and the message has to go at the speed of light or slower.

• If you force a particle that you have to accept a certain state, this will not change the state of the entangled particle. On the contrary, it will destroy the entanglement, so that you will not learn anything about the second particle.



[ Ethan didn’t fully reveal the essence of the problem. All of the above may not surprise you if you imagine an analogy with gloves. Someone sent you one glove from a pair, and your friend another. And you, having opened your parcel, instantly recognize not only which glove, left or right, you received, but also what your friend received. However, in the case of entangled particles, the state of the “gloves” is not initially defined. And we do not just do not know or do not know how to determine it - it is actually determined randomly, and it is at the time of the measurement of one of the “gloves”. Then another “glove” instantly assumes the opposite state. That is what Einstein called the “frightening long-range action” / approx. trans. ]





If two particles are entangled, the properties of their wave functions complement each other, and the measurement of one of them determines the properties of the other. But is the wave function an abstract mathematical description, or is it the basis of the deeper truth of the Universe and deterministic, fundamental reality? This is an open question.



This is a philosophical problem for realists. This means that the wave function of a particle - or the entangled wave function of several particles - is a real, physical object that exists and evolves in the Universe, but this requires a large number of uncomfortable assumptions. It must be assumed that there are an infinite number of possible realities, and that we live only in one of them, although there is no evidence of the existence of others. If you are an instrumentalist (as an author; it is simpler and more practical), you do not have this philosophical problem. You simply accept, as a given, that the wave function is a tool for calculations.





Einstein was a staunch realist in questions of quantum mechanics, and this prejudice he took with him to the grave. No evidence was found to support his interpretation of quantum mechanics, although she still has many adherents.



Stephen Weinberg, a Nobel laureate, co-founder of the Standard Model and a brilliant theoretical physicist in many fields, recently condemned the instrumentalism approach in Science News, describing it like this:



It's so terrible to imagine that we have no knowledge about everything that exists - we can say what happened only after taking a measurement.



But regardless of your philosophical evasions, quantum mechanics works, and the wave function, which confuses particles, makes it possible to destroy this entanglement, even at cosmic distances. This is the only instantaneous process in the Universe known to us, and therefore it really stands alone!



Ethan Siegel - astrophysicist, popularizer of science, blog Starts With A Bang! He wrote the books Beyond The Galaxy , and Treknologiya: Star Trek Science [ Treknology ].