Understanding particle physics: 3) waves, classic view
1. A ball on a spring, the Newtonian version
2. Quantum ball on spring
3. Waves, classic look
4. Waves, the classical equation of motion
5. Quantum waves
6. Fields
7. Particles are quanta
8. How particles interact with fields
Having dealt with the equations for vibrations — describing practically everything that jumps, vibrates, rolls back and forth like a ball on a spring — you can move on to the equally common nature phenomenon, waves. Waves are everywhere: sound and light, earthquakes, ripples on the surface of a pond, etc.

Fig. one
But before that I warn you that the term “wave” can be misleading, since in physics it means not the same as in English. In physics, it does not mean what we normally would call a wave at the edge of the ocean — one ridge and one depression. In physics, waves are a sequence of waves, several ridges and valleys, moving together in the same direction. The simplest wave has all the crests of the same height and are one distance apart from each other. We will consider just such a case.
Waves - an outstanding phenomenon, if you think about it. Imagine that you and a friend took a long rope and pulled it tight in the room (Fig. 2). Then imagine that your friend chatted up and down several times with one end of the rope (green). A wave will appear at its end of the rope, and it will pass around the room to your end of the rope (red).
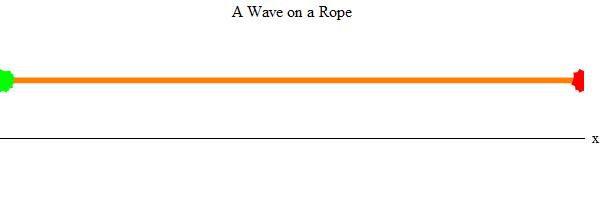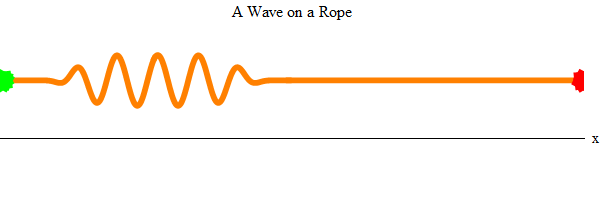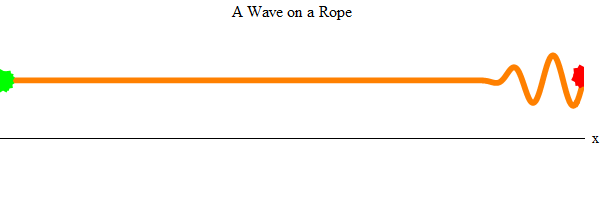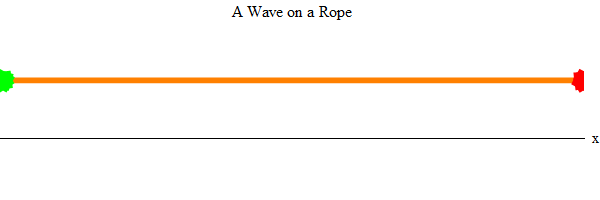
Fig. 2
It's amazing. I mean - in fact, amazingly, strongly and critically important for everything in our Universe, including you personally. See what happened. From left to right, not a single physical object moved - before your friend began to move the end of the rope, she was stretched across the room, and in the end, after your end of the rope finished oscillating and the wave disappeared, the rope would remain stretched through the room as it was. And still! Energy and information moved around the room. A wave on the way transfers the energy that your friend spent on vibrations of the rope - and carries in its form information about how many times and how quickly he pulled it - to you, where it causes your hand to shake. And in this case, she even shakes your hand just as many times and in that order. Wow! Not a single physical object moved across the room, and energy and information moved.
Or wait. Shouldn't we consider the wave as a physical object? The same physical as the rope itself?
Remembering this deepest question, we turn to a small number of mathematical formulas needed to describe the appearance and behavior of a wave, and then use a little more mathematics to write equations, the solutions of which will be waves. This is similar to what we did for a classic ball on a spring.
This series of articles immediately after the ball on the spring goes to the waves because the wave is a kind of double oscillator. It fluctuates both in time and in space. Time we denote the letter "t", and the space - "x".
Pay attention to fig. 3. It depicts a wave extending in both directions for a long distance, on which many ridges and depressions fit. This is different from the wave in fig. 2, which has only a few ridges and valleys. But this difference is irrelevant to the case - in fig. 2 I needed to illustrate something for which the exact waveform did not matter; now we will concentrate on the mathematical formula for the waves, and this is much easier to do if the wave has a large number of ridges and valleys of the same size. This case will also be very helpful in understanding how quantum mechanics affect the behavior of waves.
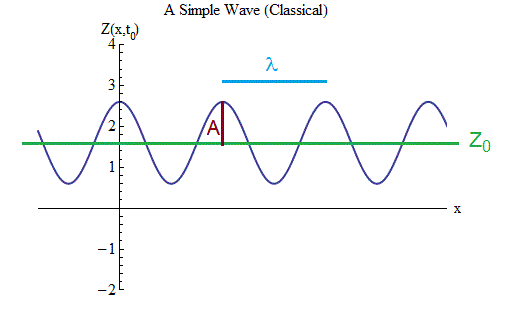

Fig. 3
First we need to decide on the notation and write down the formula describing the movement and waveform in Fig. 3, as we did for the ball on the spring.
The graph shows the magnitude of the wave Z as a function of space in a certain period of time t = t 0 - we write this as Z (x, t 0 ). By tracking the wave in space, we see that it oscillates back and forth, and Z periodically increases and decreases. At any time, the wave oscillates in space.
Note that Z does not have to be related to physical distance. This may be the height of the rope, as in fig. 2, or it may be something completely different, for example, the air temperature at a certain point in space and time or the orientation of a magnetic atom in a certain place of a magnet. But x still represents the physical distance, and t is time.
The snapshot of this wave, Z (x, t 0 ), has three interesting properties, two of which also apply to the ball on the spring.
1. There is an equilibrium value Z 0 lying midway between the largest Z value on the ridge and the smallest Z value in the trough. Most of the time we study waves in which Z 0 = 0, since often the value of Z 0 does not matter - but not always.
2. The wave has amplitude A, the magnitude by which Z changes from the equilibrium value to the top of each ridge or by the same amount to the bottom of each trough.
3. A wave has a length - the distance λ between adjacent ridges, or, which is the same, between adjacent cavities, or, which is the same, twice the distance between adjacent ridges and hollows. It describes oscillations in space in the same way as a period (equal to 1 / frequency) describes the oscillation in time of a ball on a spring.

Fig. four
What reminds us of the form in Fig. 3? It looks like a graph of a sine or cosine function - see fig. 4, where cos (w) is plotted on w. Cos (w) is an oscillating function, which has an obvious equilibrium position at zero, its amplitude is 1, and its wavelength is 2π. How to go from pic. 4 to the wave formula in fig. 3? First, we multiply cos (w) by A to make the amplitude equal to A. Then we add Z 0 to the whole formula to shift it to the desired equilibrium value (if A = 0, then there is no oscillation and everything is at rest at point Z = Z 0 ). And finally, we replace w by 2πx / λ, since cos (w) has crests at w = 0 and w = 2 π, therefore cos (2πx / λ) will have crests at x = 0 and x = λ. All together it gives us
This is practically the same formula that described the motion of a ball on a spring in time:
Where ν is the oscillation frequency, and T = 1 / ν is the oscillation period. You see an analogy: a period refers to time, as the wavelength to space.
One more note before we continue. I could write also:
Because cos [w] = cos [-w]. The fact that we can safely substitute a minus in the waveform formula will be important later.
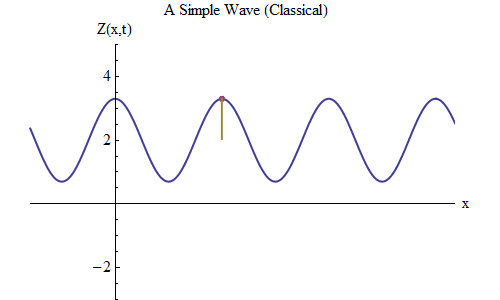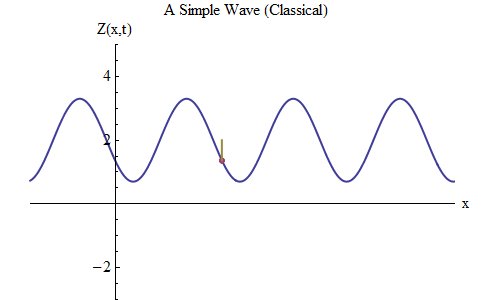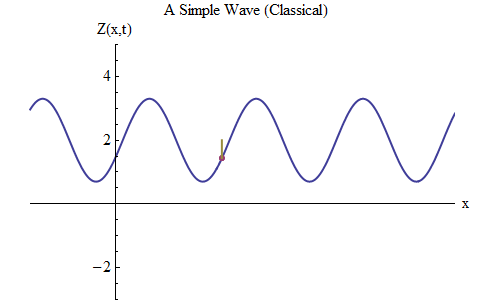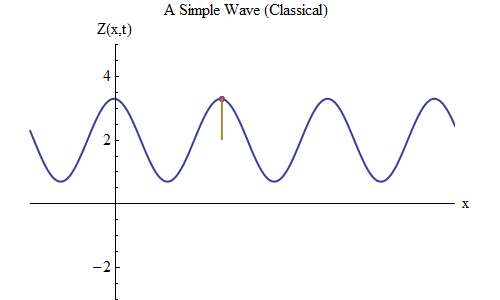
Fig. five
Now let's ask another question: let's see how the wave changes in time, tracking a certain point on the rope, and see how it behaves and moves. This is shown in fig. 5: there I marked a certain point x 0 , which at time t 0 is on the ridge. The wave moves to the right and follows the size of the wave Z at the point x 0 , changing in time: Z (x 0 , t). And you will immediately see that the wave height at a certain point behaves exactly the same as a ball on a spring! Therefore, it will have exactly the same formula as the ball on the spring, as a function of frequency ν, or of period T = 1 / ν, where T is the time between the moment when the wave at x 0 is on the crest and the moment when she again approaches the ridge next time.
Now we need a formula for Z (x, t) describing the wave shown in Fig. 3 and 5 (or any similar) at points x at any moment of time t. Correct answer:
It includes both formulas, for a fixed point in time and for a fixed point in space.
Note the minus sign in front of x. I mentioned that in the formula for Z (x, t 0 ) you can substitute a minus at will. With a minus in front of x and a plus in front of t, the formula describes a wave moving to the right, like in animations. To check this, notice that when t / T - x / λ = 0, the wave will be a crest, because cos [0] = 1. When t = 0, at the point x = 0 is a ridge. But if we move t forward slightly, say, at T / 10, the ridge will be at x = λ / 10, to the right of the place where it was at t = 0 - therefore the ridge (and the whole wave) moves to the right.
What will change if you place a plus instead of a minus in the formula for Z (x, t)? Then the ridge will be at the point t / T + x / λ = 0, and in this case at time t = T / 10 the ridge will be at the point x = -λ / 10, to the left of the place where it was at t = 0 - it means , now the wave is moving to the left (Fig. 6).
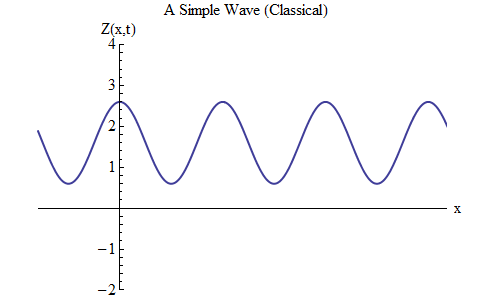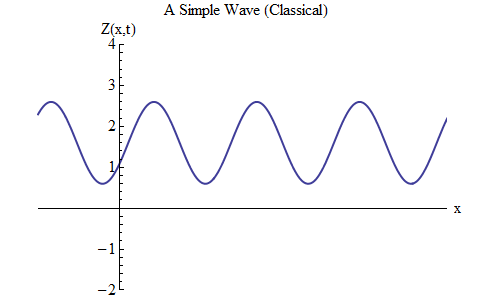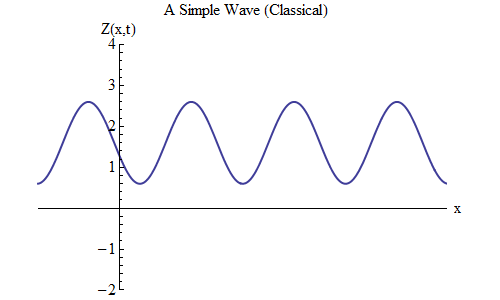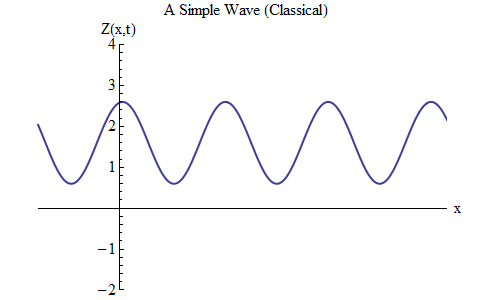
Fig. 6
Waves that are functions of x and t can move in any direction, so we just need to choose the right formula for a given wave. Generally speaking, when we work with waves that can move not only along one spatial dimension x, but along all three coordinates x, y and z, then these waves can move in any direction, and we will need to choose the right formula based on the direction motion wave.
Small print: we can put a minus sign in front of t, not in front of x. But + t, + x is the same as –t, -x, since this will be equivalent to multiplying the entire formula inside the cosine by -1, and cos [w] = cos [-w]. Therefore, + t, + x and -t, -x give a wave moving to the left, and + t, -x and -t, + x give a wave moving to the right.
Now, as in the case for the ball on the spring, when we first found the formula for the oscillatory motion of the ball, and then we looked at the equation of motion for which this formula was a solution, we will do the same here. We have found a formula for the shape and movement of the wave. Which equation of motion among the solutions found such a formula? We learn in the next article.
2. Quantum ball on spring
3. Waves, classic look
4. Waves, the classical equation of motion
5. Quantum waves
6. Fields
7. Particles are quanta
8. How particles interact with fields
Having dealt with the equations for vibrations — describing practically everything that jumps, vibrates, rolls back and forth like a ball on a spring — you can move on to the equally common nature phenomenon, waves. Waves are everywhere: sound and light, earthquakes, ripples on the surface of a pond, etc.

Fig. one
But before that I warn you that the term “wave” can be misleading, since in physics it means not the same as in English. In physics, it does not mean what we normally would call a wave at the edge of the ocean — one ridge and one depression. In physics, waves are a sequence of waves, several ridges and valleys, moving together in the same direction. The simplest wave has all the crests of the same height and are one distance apart from each other. We will consider just such a case.
Waves - an outstanding phenomenon, if you think about it. Imagine that you and a friend took a long rope and pulled it tight in the room (Fig. 2). Then imagine that your friend chatted up and down several times with one end of the rope (green). A wave will appear at its end of the rope, and it will pass around the room to your end of the rope (red).

Fig. 2
It's amazing. I mean - in fact, amazingly, strongly and critically important for everything in our Universe, including you personally. See what happened. From left to right, not a single physical object moved - before your friend began to move the end of the rope, she was stretched across the room, and in the end, after your end of the rope finished oscillating and the wave disappeared, the rope would remain stretched through the room as it was. And still! Energy and information moved around the room. A wave on the way transfers the energy that your friend spent on vibrations of the rope - and carries in its form information about how many times and how quickly he pulled it - to you, where it causes your hand to shake. And in this case, she even shakes your hand just as many times and in that order. Wow! Not a single physical object moved across the room, and energy and information moved.
Or wait. Shouldn't we consider the wave as a physical object? The same physical as the rope itself?
Remembering this deepest question, we turn to a small number of mathematical formulas needed to describe the appearance and behavior of a wave, and then use a little more mathematics to write equations, the solutions of which will be waves. This is similar to what we did for a classic ball on a spring.
Formula for an infinite wave at a certain point in time
This series of articles immediately after the ball on the spring goes to the waves because the wave is a kind of double oscillator. It fluctuates both in time and in space. Time we denote the letter "t", and the space - "x".
Pay attention to fig. 3. It depicts a wave extending in both directions for a long distance, on which many ridges and depressions fit. This is different from the wave in fig. 2, which has only a few ridges and valleys. But this difference is irrelevant to the case - in fig. 2 I needed to illustrate something for which the exact waveform did not matter; now we will concentrate on the mathematical formula for the waves, and this is much easier to do if the wave has a large number of ridges and valleys of the same size. This case will also be very helpful in understanding how quantum mechanics affect the behavior of waves.


Fig. 3
First we need to decide on the notation and write down the formula describing the movement and waveform in Fig. 3, as we did for the ball on the spring.
The graph shows the magnitude of the wave Z as a function of space in a certain period of time t = t 0 - we write this as Z (x, t 0 ). By tracking the wave in space, we see that it oscillates back and forth, and Z periodically increases and decreases. At any time, the wave oscillates in space.
Note that Z does not have to be related to physical distance. This may be the height of the rope, as in fig. 2, or it may be something completely different, for example, the air temperature at a certain point in space and time or the orientation of a magnetic atom in a certain place of a magnet. But x still represents the physical distance, and t is time.
The snapshot of this wave, Z (x, t 0 ), has three interesting properties, two of which also apply to the ball on the spring.
1. There is an equilibrium value Z 0 lying midway between the largest Z value on the ridge and the smallest Z value in the trough. Most of the time we study waves in which Z 0 = 0, since often the value of Z 0 does not matter - but not always.
2. The wave has amplitude A, the magnitude by which Z changes from the equilibrium value to the top of each ridge or by the same amount to the bottom of each trough.
3. A wave has a length - the distance λ between adjacent ridges, or, which is the same, between adjacent cavities, or, which is the same, twice the distance between adjacent ridges and hollows. It describes oscillations in space in the same way as a period (equal to 1 / frequency) describes the oscillation in time of a ball on a spring.

Fig. four
What reminds us of the form in Fig. 3? It looks like a graph of a sine or cosine function - see fig. 4, where cos (w) is plotted on w. Cos (w) is an oscillating function, which has an obvious equilibrium position at zero, its amplitude is 1, and its wavelength is 2π. How to go from pic. 4 to the wave formula in fig. 3? First, we multiply cos (w) by A to make the amplitude equal to A. Then we add Z 0 to the whole formula to shift it to the desired equilibrium value (if A = 0, then there is no oscillation and everything is at rest at point Z = Z 0 ). And finally, we replace w by 2πx / λ, since cos (w) has crests at w = 0 and w = 2 π, therefore cos (2πx / λ) will have crests at x = 0 and x = λ. All together it gives us
This is practically the same formula that described the motion of a ball on a spring in time:
Where ν is the oscillation frequency, and T = 1 / ν is the oscillation period. You see an analogy: a period refers to time, as the wavelength to space.
One more note before we continue. I could write also:
Because cos [w] = cos [-w]. The fact that we can safely substitute a minus in the waveform formula will be important later.
Formula for an infinite wave in a certain place

Fig. five
Now let's ask another question: let's see how the wave changes in time, tracking a certain point on the rope, and see how it behaves and moves. This is shown in fig. 5: there I marked a certain point x 0 , which at time t 0 is on the ridge. The wave moves to the right and follows the size of the wave Z at the point x 0 , changing in time: Z (x 0 , t). And you will immediately see that the wave height at a certain point behaves exactly the same as a ball on a spring! Therefore, it will have exactly the same formula as the ball on the spring, as a function of frequency ν, or of period T = 1 / ν, where T is the time between the moment when the wave at x 0 is on the crest and the moment when she again approaches the ridge next time.
Complete formula of infinite wave
Now we need a formula for Z (x, t) describing the wave shown in Fig. 3 and 5 (or any similar) at points x at any moment of time t. Correct answer:
It includes both formulas, for a fixed point in time and for a fixed point in space.
Note the minus sign in front of x. I mentioned that in the formula for Z (x, t 0 ) you can substitute a minus at will. With a minus in front of x and a plus in front of t, the formula describes a wave moving to the right, like in animations. To check this, notice that when t / T - x / λ = 0, the wave will be a crest, because cos [0] = 1. When t = 0, at the point x = 0 is a ridge. But if we move t forward slightly, say, at T / 10, the ridge will be at x = λ / 10, to the right of the place where it was at t = 0 - therefore the ridge (and the whole wave) moves to the right.
What will change if you place a plus instead of a minus in the formula for Z (x, t)? Then the ridge will be at the point t / T + x / λ = 0, and in this case at time t = T / 10 the ridge will be at the point x = -λ / 10, to the left of the place where it was at t = 0 - it means , now the wave is moving to the left (Fig. 6).

Fig. 6
Waves that are functions of x and t can move in any direction, so we just need to choose the right formula for a given wave. Generally speaking, when we work with waves that can move not only along one spatial dimension x, but along all three coordinates x, y and z, then these waves can move in any direction, and we will need to choose the right formula based on the direction motion wave.
Small print: we can put a minus sign in front of t, not in front of x. But + t, + x is the same as –t, -x, since this will be equivalent to multiplying the entire formula inside the cosine by -1, and cos [w] = cos [-w]. Therefore, + t, + x and -t, -x give a wave moving to the left, and + t, -x and -t, + x give a wave moving to the right.
Wave motion equation
Now, as in the case for the ball on the spring, when we first found the formula for the oscillatory motion of the ball, and then we looked at the equation of motion for which this formula was a solution, we will do the same here. We have found a formula for the shape and movement of the wave. Which equation of motion among the solutions found such a formula? We learn in the next article.
All Articles