元の記事は英語で書かれており、Standart MLの実装を使用しています。 率直に言って、私は上記の記事からすべてを盗み、英語をロシア語に翻訳し(私自身の言葉で)、Standart MLはErlangに翻訳し、何かを(もっと)捨て、何かを(少し)追加しました。 好奇心の強い読者が違いを見ることができるように、元のStandart MLとErlangの両方でコード例が提供されます。
なぜそれが必要ですか
この記事はすぐに興味を持ち、そのような視覚化のための既成のプログラムを入手したかったのです。 いいえ、一部の有用な用途ではありませんが、記事と同じ結論を得たいという願望のためだけです。 途中で、Erlangをいじって、なじみのないStandart MLの構文に慣れることができます。
問題と解決策
一番下の行は、各ノードにテキストラベルが付いたツリーを作成し、それらに位置を割り当てて、画面に美しく、審美的にツリーを描画します。 ツリー内で同じ深さのノードが同じレベルで描画されることに同意するため、問題は各ノードの水平位置を見つけることになります。 しかし、それは審美的かつ美しく意味するのでしょうか? 美しさと美学を明確に定義するルールをリストします 。
- 同じレベルにある2つのノードは、少なくとも一定の距離にある必要があります。
- 親ノードは、子ノードに対して相対的に中央に配置する必要があります。
- ツリーの描画は対称的であり、反射を考慮に入れる必要があります-ツリーとそのノードのミラー反射は、相互の反射である画像を生成する必要があります。
- 同一のツリーは同じ方法で描画する必要があります-大きなツリー内のノードの位置は、描画方法に影響を与えません。
ルール3の例:

ルール4の例:
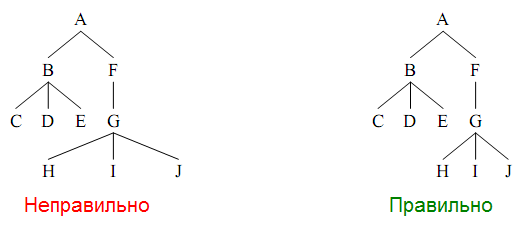
表現の問題は次のように解決されます。 まず、リストされているルールに違反しないように、すべての子ノードを描画します。 ルール1と3に違反しないように、形状を変更せずに合わせます(ルール4を破ります)。最後に、親ノードを子ノードに対して中央に配置し、処理を完了します。
重要な操作は、サブツリーの適合です。 各サブツリーにはスペースがあります-ツリーの周りの空の領域です。 サブツリーの形状は変更すべきではないため、それらのスペースは可能な限りぴったりと収まります。 残念ながら、この場合のサブツリーの最終位置は、適合する順序に依存します。 同一スペースの2つの異なる適合の例:

サブツリーを左または右のいずれかに適合させ、対応する方向にそれらをバイパスできます。 ルール3に違反しないように、両方のアクションを実行し、結果はこれら2つのラウンドの算術平均になります。
ツリービュー
オリジナルでは、ツリーの表現のために、MLポリモーフィズムを使用し、次のようにデータを記述します。
データ型 'a Tree = Node of' a *( 'aツリーリスト)
これは、ノードが値(タイプ 'a)と子ツリーのリストで構成されることを意味します。 オリジナルでは、アルゴリズムは「a Tree」タイプの入力ツリーを受け取り、「(* a * real)Tree」タイプの配置済みツリーを返します。 ここで、2番目の要素には、親ノードに対するノードの水平位置が格納されます 。 Erlangのポリモーフィズムについては何も知らないので、ノードのデータ型は1つだけであり、すでに水平位置が含まれています。
-record(pnode、{label = "LABEL"、pos = 0、children = []})。
ノードの相対位置を使用することにしたので、ノードをシフトする操作は一定の時間で実行できます。
fun movetree(Node((label、x)、subtrees)、x ':real)=
ノード((ラベル、x + x ')、サブツリー)
move_ptree({[]、_X})-> [];
move_ptree({#pnode {pos = Pos} = Node、X})->
ノード#pnode {pos = Pos + X}。
スペースビュー
ツリー空間は、MLのペアとErlangのペアのリストで表されます。
タイプExtent =(real * real)list
-record(エクステント、{左、右})。
ペアのコンポーネントには、それぞれスペースの左右の境界が含まれます。 リストの最初のペアは、ツリーのルートに対応しています。 ツリーの表現とは対照的に、空間の位置は絶対的であることに言及することが重要です。
スペースを水平方向に移動する関数は次のようになります。
fun moveextent(e:Extent、x)= map(fn(p、q)=>(p + x、q + x))e
move_extent({#エクステント{左=左、右=右} =エクステント、オフセット})->
エクステント#エクステント{左=左+オフセット、右=右+オフセット};
move_extent({ExtentList、Offset})->
リスト:マップ(fun(Extent)-> move_extent({Extent、Offset})end、ExtentList)。
Erlangバージョンでは、読者は関数の引数でタプルが奇妙に使用されていることに気付いたに違いありません。 このスタイルは、 リストの利便性を高めるために、次の関数の多くで使用されます:zip 。
また、 2つの独立したスペースを組み合わせて 、それらの間の穴を埋める必要があります。 これは、最初のスペースの左の位置の座標と2番目のスペースの右の位置の座標を取得することによって行われます。
楽しいマージ([]、qs)= qs
| マージ(ps、[])= ps
| merge((p、_):: ps、(_、q):: qs)=(p、q):: merge(ps、qs)
元の記事の著者は、さまざまな深さのスペースのリストがどのように処理されるかに注目しています。 Erlangでは、次のようになります。
merge_extent({#エクステント{左=左}、#エクステント{右=右}})->
#extent {left = Left、right = Right};
merge_extent({[]、[]})-> [];
merge_extent({[]、エクステント})->エクステント;
merge_extent({Extent、[]})->エクステント;
merge_extent({[左|左レスト]、[右|右レスト]})->
[merge_extent({左、右})| merge_extent({LeftRest、RightRest})]。
この操作は、次のようにスペースのリストに拡張できます。
fun mergelist es = fold merge es []
merge_extent_list(ExtentList)->
リスト:foldl(fun(Elem、Acc)-> merge_extent({Acc、Elem})end、[]、ExtentList)。
私からは、Erlangのオプションに特別かつ細心の注意を払うようお願いします。 2つの引数が畳み込みの最初の引数-ラム関数-Elem、Accに渡されます。 ただし、merge_extentでは、逆の順序で渡されます:Acc、Elem。 Erlangのコードを引き裂いていたとき、私はこれに気付かずに気付かず、同じ順序にしました。 その結果、スペースの結合は間違った場所で機能し、ツリーの一部で結論が曲がりました。
誤動作の原因をよりよく理解するために、この関数への入力(間違ったオプション)の場合に何が起こるかを考慮してください。
merge_extent_list(ExtentList)->
リスト:foldl(fun(Elem、Acc)-> merge_extent({Elem、Acc})end、[]、ExtentList)。
そのような値は次のとおりです。
[[{extent、-80、-73}]]、
[{extent、-48、-41}]、
[{extent、-16、-9}]、
[{extent、16.23}]、
[{extent、48.55}]、
[{extent、80.87}]]
merge_extentの引数がラムへの入力と同じ順序で渡されたとき、次のデバッグ出力を確認しました。
merge_extent:Ex1:{extent、-48、-41}、Ex2:{extent、-80、-73}
merge_extent:結果:{extent、-48、-73}
merge_extent:Ex1:{extent、-16、-9}、Ex2:{extent、-48、-73}
merge_extent:結果:{extent、-16、-73}
merge_extent:Ex1:{extent、16,23}、Ex2:{extent、-16、-73}
merge_extent:結果:{extent、16、-73}
merge_extent:Ex1:{extent、48.55}、Ex2:{extent、16、-73}
merge_extent:結果:{extent、48、-73}
merge_extent:Ex1:{extent、80.87}、Ex2:{extent、48、-73}
merge_extent:結果:{extent、80、-73}
merge_extent_list:結果:[{extent、80、-73}]
ご覧のとおり、奇妙なスペース{extent、80、-73}があります。ここで、左側の境界線は右側にあります。 その理由は、merge_extent関数を見れば簡単にわかります。 ただし、引数の順序を変更しない場合、この「間違った」オプションは、左側の畳み込みを右側の畳み込みに置き換えることで正しく作成できます。foldlをfoldrに置き換えます。
奇妙なことですが、著者の以下の記事では、「マージは結合的であるため、代わりに左結合バージョンのfoldを使用できました」(「結合関数は結合的であるため、左結合畳み込みを使用できます」) 私は何かを理解していなかったかもしれませんが、私の意見ではこれは嘘であり挑発です 何か見落とした場合は修正してください。
merge_extent_list関数の使用例を図に示します。

空間フィット
最初に、2つのツリーが互いにどれだけ近いかを決定する関数を作成します。 この関数は、入力として2つのスペースを取り、ノード間の可能な最小距離を返します。
fun rmax(p:実数、q:実数)= if p> q then p else q fun fit((_、p):: ps)((q、_):: qs)= rmax(fit ps qs、p-q + 1.0) | フィット_ _ = 0.0
fit_extent({#エクステント{右=右}、#エクステント{左=左}})->
右-左+?EXTENT_SEPARATOR;
fit_extent({[]、[]})->
0;
fit_extent({[[First | FirstRest]、[Second | SecondRest]})->
erlang:max(fit_extent({First、Second})、fit_extent({FirstRest、SecondRest}));
fit_extent({_ A、_B})->
0。
元の記事では、最小距離は1.0であり、定数を使用しました。
-define(EXTENT_SEPARATOR、15)。
次に、この関数をスペースのリストに展開します。 左端の位置がゼロであると仮定して、それぞれの位置を計算します。 この関数は、結果のスペースを累積し、次のスペースに交互にフィットさせることにより機能します。 リストは左から右にクロールされるため、関数の結果は非対称です。
楽しいfitlistl es =
させる
fun fitlistl 'acc [] = []
| fitlistl 'acc(e :: es)=
let val x = fit acc e
で
x :: fitlistl '(merge(acc、moveextent(e、x)))es
終わり
で
fitlistl '[] es
終わり
fit_extent_list_l(ExtentList)->
fit_extent_list_l([]、ExtentList)。
fit_extent_list_l(_Acc、[])-> [];
fit_extent_list_l(Acc、[Extent | Rest])->
X = fit_extent({Acc、Extent})、
[X | fit_extent_list_l(merge_extent({Acc、move_extent({Extent、X})})、Rest)]。
次の関数では逆の効果が得られます。この関数は、位置がゼロの右端のスペースを基準にして位置を計算します。 ここで、revはリストの反転で、〜は符号の否定です。
楽しいfitlistr es =
させる
fun fitlistr 'acc [] = []
| fitlistr 'acc(e :: es)=
let val x =〜(フィットe acc)
で
x :: fitlistr '(merge(moveextent(e、x)、acc))es
終わり
で
rev(fitlistr '[](rev es))
終わり
fit_extent_list_r(ExtentList)->
リスト:リバース(fit_extent_list_r([]、リスト:リバース(ExtentList)))。
fit_extent_list_r(_Acc、[])-> [];
fit_extent_list_r(Acc、[Extent | Rest])->
X =-fit_extent({Extent、Acc})、
[X | fit_extent_list_r(merge_extent({move_extent({Extent、X})、Acc})、Rest)]。
ただし、後者の機能は別の方法で実装できます。 fitlistrは、関数合成を使用してfitlistlで定義できます。
val flipextent:エクステント->エクステント=マップ(fn(p、q)=>(〜q、〜p)) val fitlistr = rev o map〜o fitlistl o map flipextent o rev
flip_extent(#extent {左=左、右=右} =範囲)->
エクステント#エクステント{左=-右、右=-左};
flip_extent(ExtentList)->
[flip_extent(エクステント)|| エクステント<-ExtentList]。
fit_extent_list_r(ExtentList)->
リスト:逆(
[-X || X <-fit_extent_list_l(
リスト:マップ(
fun flip_extent / 1、
リスト:reverse(ExtentList)
)
)]
)
最後に、ツリーの表示の対称性を実現するために、両方の方法で位置を計算し、その結果の平均を取ります。
楽しい平均(x、y)=(x + y)/2.0 fun fitlist es = map mean(zip(fitlistl es、fitlistr es))
平均({X、Y})->
trunc((X + Y)/ 2)。
fit_extent_list(ExtentList)->
リスト:マップ(
楽しい平均/ 1、
リスト:zip(fit_extent_list_l(ExtentList)、fit_extent_list_r(ExtentList))
)
ツリー編集
ここで、すべてのコンポーネントをまとめて、ノード内のラベルを持つツリーを取得し、同じツリーを生成するが、各ノードの座標を持つ関数を作成します。 ツリーのルートの位置はゼロです。
楽しいデザインツリー=
させる
楽しいデザイン '(ノード(ラベル、サブツリー))=
させる
val(ツリー、エクステント)= unzip(マップデザイン 'サブツリー)
val位置=フィットリスト範囲
val ptrees =マップmovetree(zip(ツリー、位置))
val pextents =マップmoveextent(zip(エクステント、位置))
val resultextent =(0.0、0.0):: mergelist pextents
val resulttree = Node((label、0.0)、ptrees)
で
(resulttree、resultextent)
終わり
で
fst(デザイン 'ツリー)
終わり
design_tree(#pnode {ラベル=ラベル、子= []})->
{make_pnode(ラベル、0、[])、[make_extent(0、0)]};
design_tree(#pnode {label = Label、children = Children} = Node)->
{Trees、Extents} =リスト:unzip(リスト:map(fun design_tree / 1、Children))、
位置= fit_extent_list(範囲)、
PTrees =リスト:マップ(fun move_ptree / 1、リスト:zip(ツリー、位置))、
PExtents =リスト:マップ(fun move_extent / 1、リスト:zip(エクステント、位置))、
ResultExtent = [make_extent(0、0)| merge_extent_list(PExtents)]、
ResultTree = Node#pnode {pos = 0、children = PTrees}、
{ResultTree、ResultExtent}。
仕組みは次のとおりです。最初に、すべてのツリーが再帰的にコンパイルされます。 結果はペア(ツリー、エクステント)のリストであり、これにunzipを適用して2つのリストを取得します。 すべてのサブツリーのルートの位置はゼロです。 次に、fillist(fit_extent_list)関数を使用してスペースを調整し、位置のオフセットのリストを取得します。 次に、ツリー内の各サブツリーを位置からの対応するオフセットにシフトし、ptreeを取得します。 スペースに対しても同じことを行い、pextentsを取得します。 結論として、結果の空間とゼロ位置にルートを持つツリーを計算します。
アルゴリズムの複雑さ
提示されたアルゴリズムの複雑さは、最悪の場合O(n²)です。ここで、 nはツリー内のノードの数です。 幸いなことに、線形の複雑さを達成するためにプログラムを書き換えることができますが、コードの明確さはいくらか失われます。 非効率は、スペースの表示に起因します。 ツリーの移動には、座標の相対性のために一定の時間が必要であり、空間の移動には絶対座標の使用による線形の複雑さがあります。 相対座標を使用すると、mergelist(merge_extent_list)の複雑さが2次から線形に減少します。 残念ながら、fit(fit_extent)およびmerge(merge_extent)関数はエレガントではなくなります。
樹木画
元の記事では、コードを生成せずにツリーのグラフィカル表現が突然表示されます。 したがって、私自身からこのようなコードの例をErlangに追加します。
-define(LAYER_HEIGHT、30)。
-define(LINE_Y_OFFSET、10)。
-define(LINE_X_OFFSET、3)。
-define(LINE_VERTICAL_LENGTH、7)。
draw_designed_tree(キャンバス、X、Y、
#pnode {label = Label、pos = Pos、children = Children})->
NewX = X +?LINE_X_OFFSET、
NewY = Y-?LINE_Y_OFFSET、
gs:line(Canvas、[{coords、[
{NewX、NewY-?LINE_VERTICAL_LENGTH}、
{NewX、NewY}、
{NewX + Pos、NewY}、
{NewX + Pos、NewY +?LINE_VERTICAL_LENGTH}
]}])、
gs:テキスト(キャンバス、[
{coords、[{X + Pos、Y}]}、
{テキスト、ラベル}
])、
リスト:マップ(
fun(ノード)->
draw_designed_tree(キャンバス、X + Pos、Y +?LAYER_HEIGHT、ノード)
終わり
子供)
わかった
この関数では、ノード間の接続線が最初に描画され、次にノードラベルのテキストが描画され、最後に各子ノードで操作が繰り返されます。
テストツリーを作成する
完全を期すために、テストツリーを作成するコードを提供します。
ツリー= add_pnodes(
add_pnode(
make_pnode( "@")、
add_pnodes(
make_pnode( "B")、
[make_pnode( "C")、
add_pnodes(
make_pnode( "D")、
[make_pnode( "1")、
make_pnode( "2")]
)、
make_pnode( "E")、
add_pnodes(
make_pnode( "F")、
[make_pnode( "1")、
make_pnode( "2")、
make_pnode( "3")、
make_pnode( "4")、
make_pnode( "5")、
make_pnode( "6")]
)、
add_pnodes(
make_pnode( "G")、
[make_pnode( "1")、
make_pnode( "2")、
make_pnode( "3")、
make_pnode( "4")、
make_pnode( "5")]
)、
make_pnode( "H")、
make_pnode( "I")、
make_pnode( "J")]
)
)、
[add_pnodes(
make_pnode( "K")、
[make_pnode( "L")、
make_pnode( "M")、
make_pnode( "N")、
make_pnode( "O")、
make_pnode( "P")]
)、
make_pnode( "Q")、
make_pnode( "R")、
make_pnode( "S")、
make_pnode( "T")]
)、
グラフィカル出力
記事の著者がしたことは次のとおりです。
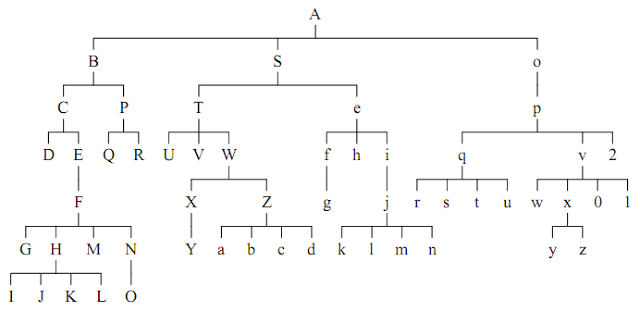
ここに私が得たものがあります:

ファイル仕上げ
私は本当に1文字ではなく、ノードラベルに単語を書きたいと思っていました。 幸いなことに、これは簡単に解決できます。 design_tree関数では、ノードラベルのテキスト幅を考慮してスペースの作成を修正する必要があります。2番目の引数make_extent(0、0)を実世界のものに置き換えます。 私はgsでテキストの幅を取得する関数を見つけられなかったので、単純にすることを決めました:ラベルの文字数に特定の係数を掛けます。 これを行うために、関数を導入します:
-define(LETTER_WIDTH、7)。
label_width(ラベル)->
?LETTER_WIDTH *長さ(ラベル)。
そして、結果のツリーを受け取るときにこの関数を使用します。 design_treeの形式は次のとおりです。
design_tree(#pnode {ラベル=ラベル、子= []})->
{make_pnode(Label、0、[])、[make_extent(0、label_width(Label))]};
design_tree(#pnode {label = Label、children = Children} = Node)->
{Trees、Extents} =リスト:unzip(リスト:map(fun design_tree / 1、Children))、
位置= fit_extent_list(範囲)、
PTrees =リスト:マップ(fun move_ptree / 1、リスト:zip(ツリー、位置))、
PExtents =リスト:マップ(fun move_extent / 1、リスト:zip(エクステント、位置))、
ResultExtent = [make_extent(0、label_width(Label))| merge_extent_list(PExtents)]、
ResultTree = Node#pnode {pos = 0、children = PTrees}、
{ResultTree、ResultExtent}。
テストします。 入力ツリーの場合:
ツリー= add_pnodes(
add_pnode(
make_pnode( "@")、
add_pnodes(
make_pnode( "ベータ版")、
[make_pnode( "コード")、
add_pnodes(
make_pnode(「パパ」)、
[make_pnode( "1st")、
make_pnode( "2dn")]
)、
make_pnode( "終了")、
add_pnodes(
make_pnode( "Fall")、
[make_pnode( "111")、
make_pnode( "222")、
make_pnode( "333")、
make_pnode( "444")、
make_pnode( "555")、
make_pnode( "666")]
)、
add_pnodes(
make_pnode(「重力」)、
[make_pnode( "1_milk")、
make_pnode( "2_apple")、
make_pnode( "3_juice")、
make_pnode( "4_banana")、
make_pnode( "5_orange")]
)、
make_pnode(「希望」)、
make_pnode(「病気」)、
make_pnode( "ジョーク")]
)
)、
[add_pnodes(
make_pnode(「カーネル」)、
[make_pnode( "Load")、
make_pnode(「モジュール」)、
make_pnode( "Nop")、
make_pnode(「演算子」)、
make_pnode( "ポイント")]
)、
make_pnode( "終了")、
make_pnode( "Rest")、
make_pnode( "Set")、
make_pnode( "終了")]
)、
私は受け取った:

結論
個人的には、私が手に入れたものよりもMLコードが好きです。 著者のコードはよりエレガントでエレガントで、はるかに宣言的ですが、後者は言語の機能に関連する可能性が高いです。
コード
著者のプログラムの完全なコードを持っていないので、自分の引用だけを引用しました( ここにコピーします ):
-モジュール(drawtree)。
-compile(export_all)。
-define(EXTENT_SEPARATOR、15)。
-define(LAYER_HEIGHT、30)。
-define(LINE_Y_OFFSET、10)。
-define(LINE_X_OFFSET、3)。
-define(LINE_VERTICAL_LENGTH、7)。
-define(LETTER_WIDTH、7)。
-define(TREE_POS_X、350)。
-define(TREE_POS_Y、30)。
-define(WINDOW_WIDTH、1000)。
-define(WINDOW_HEIGHT、500)。
-record(pnode、{label = "LABEL"、pos = 0、children = []})。
-record(エクステント、{左、右})。
init()->
S = gs:開始()、
Win = gs:window(ui_main_window、S、[{width ,? WINDOW_WIDTH}、{height ,? WINDOW_HEIGHT}])、
gs:config(Win、{map、true})、
Canvas = gs:canvas(Win、[{x、0}、{y、0}、{width ,? WINDOW_WIDTH}、{height ,? WINDOW_HEIGHT}])、
do_drawings(キャンバス)、
ループ()、
init:stop()。
move_ptree({[]、_X})-> [];
move_ptree({#pnode {pos = Pos} = Node、X})->
ノード#pnode {pos = Pos + X}。
make_extent(左、右)->
#extent {左=左、右=右}。
make_pnode(ラベル)->
#pnode {label = Label}。
make_pnode(ラベル、位置、子)->
#pnode {label = Label、pos = Pos、children = Children}。
add_pnode(#pnode {children = Children} = Tree、PNode)->
ツリー#pnode {children = [PNode | 子供]}。
add_pnodes(#pnode {children = Children} = Tree、PNodes)->
ツリー#pnode {children = PNodes ++ Children}。
do_drawings(キャンバス)->
ツリー= add_pnodes(
add_pnode(
make_pnode( "@")、
add_pnodes(
make_pnode( "ベータ版")、
[make_pnode( "コード")、
add_pnodes(
make_pnode(「パパ」)、
[make_pnode( "1st")、
make_pnode( "2nd")]
)、
make_pnode( "終了")、
add_pnodes(
make_pnode( "Fall")、
[make_pnode( "111")、
make_pnode( "222")、
make_pnode( "333")、
make_pnode( "444")、
make_pnode( "555")、
make_pnode( "666")]
)、
add_pnodes(
make_pnode(「重力」)、
[make_pnode( "1_milk")、
make_pnode( "2_apple")、
make_pnode( "3_juice")、
make_pnode( "4_banana")、
make_pnode( "5_orange")]
)、
make_pnode(「希望」)、
make_pnode(「病気」)、
make_pnode( "ジョーク")]
)
)、
[add_pnodes(
make_pnode(「カーネル」)、
[make_pnode( "Load")、
make_pnode(「モジュール」)、
make_pnode( "Nop")、
make_pnode(「演算子」)、
make_pnode( "ポイント")]
)、
make_pnode( "終了")、
make_pnode( "Rest")、
make_pnode( "Set")、
make_pnode( "終了")]
)、
io:形式(「ソース=〜p〜n」、[ツリー])、
{DesignedTree、エクステント} = design_tree(ツリー)、
io:format( "DesignedTree =〜p〜n"、[DesignedTree])、
io:format( "Extents =〜p〜n"、[Extents])、
draw_designed_tree(キャンバス、?TREE_POS_X 、? TREE_POS_Y、DesignedTree)。
move_extent({#エクステント{左=左、右=右} =エクステント、オフセット})->
エクステント#エクステント{左=左+オフセット、右=右+オフセット};
move_extent({ExtentList、Offset})->
リスト:マップ(fun(Extent)-> move_extent({Extent、Offset})end、ExtentList)。
merge_extent({#エクステント{左=左}、#エクステント{右=右}})->
#extent {left = Left、right = Right};
merge_extent({[]、[]})-> [];
merge_extent({[]、エクステント})->エクステント;
merge_extent({Extent、[]})->エクステント;
merge_extent({[左|左レスト]、[右|右レスト]})->
[merge_extent({左、右})| merge_extent({LeftRest、RightRest})]。
merge_extent_list(ExtentList)->
%重要:ElemとAccの変更に注意してください!
%fun(Elem、Acc)-> merge_extent({Acc、Elem}
リスト:foldl(fun(Elem、Acc)-> merge_extent({Acc、Elem})end、[]、ExtentList)。
fit_extent({#エクステント{右=右}、#エクステント{左=左}})->
右-左+?EXTENT_SEPARATOR;
fit_extent({[]、[]})->
0;
fit_extent({[[First | FirstRest]、[Second | SecondRest]})->
erlang:max(fit_extent({First、Second})、fit_extent({FirstRest、SecondRest}));
fit_extent({_ A、_B})->
0。
fit_extent_list_l(ExtentList)->
fit_extent_list_l([]、ExtentList)。
fit_extent_list_l(_Acc、[])-> [];
fit_extent_list_l(Acc、[Extent | Rest])->
X = fit_extent({Acc、Extent})、
[X | fit_extent_list_l(merge_extent({Acc、move_extent({Extent、X})})、Rest)]。
flip_extent(#extent {左=左、右=右} =範囲)->
エクステント#エクステント{左=-右、右=-左};
flip_extent(ExtentList)->
[flip_extent(エクステント)|| エクステント<-ExtentList]。
fit_extent_list_r(ExtentList)->
リスト:逆(
[-X || X <-fit_extent_list_l(
リスト:マップ(
fun flip_extent / 1、
リスト:reverse(ExtentList)
)
)]
)
%fit_extent_list_r(ExtentList)->
%リスト:リバース(fit_extent_list_r([]、リスト:リバース(ExtentList)))。
%fit_extent_list_r(_Acc、[])-> [];
%fit_extent_list_r(Acc、[Extent | Rest])->
%X =-fit_extent({Extent、Acc})、
%[X | fit_extent_list_r(merge_extent({move_extent({Extent、X})、Acc})、Rest)]。
平均({X、Y})->
trunc((X + Y)/ 2)。
fit_extent_list(ExtentList)->
リスト:マップ(
楽しい平均/ 1、
リスト:zip(fit_extent_list_l(ExtentList)、fit_extent_list_r(ExtentList))
)
label_width(ラベル)->
?LETTER_WIDTH *長さ(ラベル)。
design_tree(#pnode {ラベル=ラベル、子= []})->
{make_pnode(Label、0、[])、[make_extent(0、label_width(Label))]};
design_tree(#pnode {label = Label、children = Children} = Node)->
{Trees、Extents} =リスト:unzip(リスト:map(fun design_tree / 1、Children))、
位置= fit_extent_list(範囲)、
PTrees =リスト:マップ(fun move_ptree / 1、リスト:zip(ツリー、位置))、
PExtents =リスト:マップ(fun move_extent / 1、リスト:zip(エクステント、位置))、
ResultExtent = [make_extent(0、label_width(Label))| merge_extent_list(PExtents)]、
ResultTree = Node#pnode {pos = 0、children = PTrees}、
{ResultTree、ResultExtent}。
draw_designed_tree(キャンバス、X、Y、
#pnode {label = Label、pos = Pos、children = Children})->
NewX = X +?LINE_X_OFFSET、
NewY = Y-?LINE_Y_OFFSET、
gs:line(Canvas、[{coords、[
{NewX、NewY-?LINE_VERTICAL_LENGTH}、
{NewX、NewY}、
{NewX + Pos、NewY}、
{NewX + Pos、NewY +?LINE_VERTICAL_LENGTH}
]}])、
gs:テキスト(キャンバス、[
{coords、[{X + Pos、Y}]}、
{テキスト、ラベル}
])、
リスト:マップ(
fun(ノード)->
draw_designed_tree(キャンバス、X + Pos、Y +?LAYER_HEIGHT、ノード)
終わり
子供)
わかった
ループ()->
受け取る
{gs、ui_main_window、destroy、_Data、_Args}->
わかった。
_その他->
ループ()
終わり。