フィボナッチ数（C＃のスケッチ）

おそらく、多くの学生はフィボナッチ数の計算例を使用して再帰を勉強しなければならなかったでしょう。 タスクは確かに学術的なものであり、たとえば階乗を計算するよりも明らかに悪い再帰を示していますが、さまざまな程度の倒錯の多くの解決策があるという点で興味深いです。 この投稿では-このトピックに関する小さなスケッチ。





N番目のフィボナッチ数を計算するための「デフォルト」ソリューションに誰も驚かないと思います。

static int fib(int n) { return n > 1 ? fib(n - 1) + fib(n - 2) : n; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

また、Yコンビネーターを使用するこのソリューションを作成する「ファッショナブルな」形式があります。

 Func<int, int> fib = Y<int,int>(f => n => n > 1 ? f(n - 1) + f(n - 2) : n);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

たとえば、 Y



次のように定義されます。

 static Func<A, R> Y<A, R>(Func<Func<A, R>, Func<A, R>> f) { Func<A, R> g = null; g = f(a=>g(a)); return g; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Nが大きい場合、このアプローチは非生産的です。 Nの数をより速くカウントする方法は？ まず、たとえばx*x



がMath.Pow(x,2)



よりも高速であると考えられる理由を思い出しましょう。 整数次数の場合、テイラー級数なしで実行できるだけでなく、一時変数を作成することで大次数の計算を最適化することもできます。 たとえば、x ⁴はint y = x * x; return y * y;



と見なすことができますint y = x * x; return y * y;



int y = x * x; return y * y;



-そして、程度が大きいほど、節約額は大きくなります。



なぜこれをしているのですか？ さらに、フィボナッチ数は次の式を使用して計算できます。









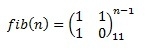
整数のべき乗が必要な理由は明らかです。 行列についても、同じことを行うことができますが、最初にこれが一般的に行われる方法を理解する必要があります。 インターネットで、おそらく整数のべき乗を最適化する完璧なアルゴリズムを見つけました。 以下の例では、次数はshort



型であることに注意してください。

 public static long IntPower(int x, short power) { if (power == 0) return 1; if (power == 1) return x; int n = 15; while ((power <<= 1) >= 0) n--; long tmp = x; while (--n > 0) tmp = tmp * tmp * (((power <<= 1) < 0) ? x : 1); return tmp; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

現在は、2×2行列を決定するだけです。 ここでは、何らかの種類のライブラリを使用できますが、可能な限り単純な構造を作成することにしました。

 struct mtx2x2 { public int _11, _12, _21, _22; public static mtx2x2 operator*(mtx2x2 lhs, mtx2x2 rhs) { return new mtx2x2 { _11 = lhs._11*rhs._11 + lhs._12*rhs._21, _12 = lhs._11*rhs._12 + lhs._12*rhs._22, _21 = lhs._21*rhs._11 + lhs._22*rhs._21, _22 = lhs._21*rhs._12 + lhs._22*rhs._22 }; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

その後、2つの定数を決定する必要がありました。これは、累乗する行列と単位行列です。

 private static readonly mtx2x2 fibMtx = new mtx2x2 {_11 = 1, _12 = 1, _21 = 1}; private static readonly mtx2x2 identity = new mtx2x2 {_11 = 1, _22 = 1};
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、2×2行列のIntPower()



メソッドを書き換えることができます。

 public static mtx2x2 IntPower(mtx2x2 x, short power) { if (power == 0) return identity; if (power == 1) return x; int n = 15; while ((power <<= 1) >= 0) n--; mtx2x2 tmp = x; while (--n > 0) tmp = (tmp * tmp) * (((power <<= 1) < 0) ? x : identity); return tmp; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、フィボナッチ数を計算するための新しい方法を定義します。

 static int fibm(short n) { return IntPower(fibMtx, (short)(n-1))._11; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

以上です。 パフォーマンスを比較しても意味がないと思いますfibm(40)



は4秒間カウントされ、 fibm(40)



は即座に表示されます。 ■