クラスは、従来の命令型言語のインターフェースと同様に動的な多相性を導入し、Haskellにない関数のオーバーロードの代替として使用することもできます。
型クラス、そのインスタンス、およびすべてが内部でどのように機能するかを定義する方法を説明します。
前の記事:
データ型、パターンマッチング、および機能
基本
型クラス
データ型を作成し、そのための比較演算子を作成するとします。 問題は、Haskellには関数のオーバーロードがないため、この目的で(==)を簡単な方法で使用しても機能しないことです。 さらに、各タイプに新しい名前を付けることはオプションではありません。
ただし、比較する型のクラスを定義できます。 次に、データ型がこのクラスに属している場合、この型の値を比較できます。
class MyEq a where
myEqual :: a -> a -> Bool
myNotEqual :: a -> a -> Bool
MyEq
は型クラスの名前(データ型など、大文字で始まる必要があります)、
a
はこのクラスに属する型です。 クラスには複数の
FooClass abc
(
FooClass abc
)がありますが、この場合は1つだけです。
対応する関数が定義されている場合、タイプは
MyEq
クラスに属します。
クラスでは、デフォルトの関数を定義できます。 たとえば、関数
myEqual
と
myNotEqual
は相互に表現できます。
このような定義は無限の再帰につながりますが、クラスインスタンスでは少なくとも1つを定義すれば十分です。myEqual xy = not ( myNotEqual xy )
myNotEqual xy = not ( myEqual xy )
Bool
クラスインスタンスを作成します。
インスタンス定義は、instance MyEq Bool where
myEqual True True = True
myEqual False False = True
myEqual _ _ = False
instance
キーワードで始まり、クラス自体の定義にあるタイプ
a
変数の代わりに、インスタンスが定義されているタイプ、つまり
Bool
。
1つの関数
myEqual
を定義し
myEqual
、インタープリターで結果を確認できます。
ghci> myEqual True True
True
ghci> myNotEqual True False
True
ghci> :t myEqual
myEqual :: (MyEq a) => a -> a -> Bool
myEqual
関数の型は、型に制約を課していることが
myEqual
ます—
MyEq
クラスに属している必要があります。
クラス自体を宣言するときに、同じ制限を課すことができます。
class ( MyEq a ) => SomeClass a where
-- ...
クラスはインターフェイスに多少似ています-関数を宣言し、そのための実装を提供します。 他の関数がこれらの関数を使用できるのは、あるタイプについてそのような実装がある場合のみです。
ただし、機能とメカニズム自体の実装の両方に大きな違いがあります。
-
myEqual
関数からmyEqual
ように、タイプa
2つの値を取りますが、仮想関数はthis
パラメーターを1つだけ受け取ります。
instance MyEq Bool
およびinstance MyEq Int
があるinstance MyEq Bool
でも、myEqual True 5
関数の呼び出しは失敗します。
コンパイラー(インタープリター)は、パラメーターghci> myEqual True (5::Int)
<interactive>:1:14:
Couldn't match expected type `Bool' against inferred type `Int'
In the second argument of `myEqual', namely `(5::Int)'
In the expression: myEqual True (5 :: Int)
In the definition of `it': it = myEqual True (5 :: Int)
ghci>
myEqual
が同じタイプでなければならないことを知っているため、そのような試みを防ぎます。 - クラスインスタンスはいつでも定義でき、これも非常に便利です。 インターフェースからの継承は、クラス自体を定義するときに示されます。
- 関数では、データ型が複数のクラスに一度に属することが必要になる場合があります。
たとえば、C ++ / C#でこれを行う方法は? 複合foo :: ( Eq a , Show a , Read a ) => a -> String -> String
IEquableShowableReadable
作成しますか? しかし、あなたは彼から相続しないでしょう。 引数を3回渡して、異なるインターフェースを導き、関数内でこれが同じオブジェクトであり、呼び出し側に責任があると仮定しますか?
すでにC ++に言及しているので、同時に、新しい標準C ++ 0x コンセプトとconcept_mapには型クラスの本質がありますが、コンパイル段階で使用されます:)
しかし、欠点があります。 たとえば、
Show
クラス(関数
show :: a -> String
)に属するオブジェクトのリストを取得するにはどうすればよいですか?
方法はありますが、非標準です。 適切なGHCオプションをファイルの先頭に追加する必要があります。
これで、このデータ型を宣言できます。{-#
OPTIONS_GHC
-XExistentialQuantification
#-}
-- , , TAB' GHC
( 存在タイプについての詳細を読む)data ShowObj = forall a . Show a => ShowObj a
同時に彼のために
Show
クラスのインスタンスを定義し、彼自身も彼に所属するようにします。
チェック:instance Show ShowObj where
show ( ShowObj x ) = show x
明示的にghci> [ShowObj 4, ShowObj True, ShowObj (ShowObj 'x')]
[4,True,'x']
show
関数を呼び出したわけではありませんが、インタープリターはそれを使用するため、すべてが機能することを確認できます。
これはどのように実装されていますか?
隠されたパラメーターは、型に制限を課す関数に渡されます(各クラスと型には独自の値があります)-すべての必要な関数を備えた辞書。
実際、
instance
は特定のタイプの辞書インスタンスの定義です。
わかりやすくするために、HaskellおよびC ++の
Eq
擬似実装を示します。
C ++でも同じこと:-- class MyEq
data MyEq a = MyEq {
myEqual :: a -> a -> Bool ,
myNotEqual :: a -> a -> Bool }
-- instance MyEq Bool
myEqBool = MyEq {
myEqual = \ xy -> x == y ,
myNotEqual = \ xy -> not ( x == y ) }
-- foo :: (MyEq a) => a -> a -> Bool
foo :: MyEq a -> a -> a -> Bool
foo dict xy = ( myEqual dict ) xy
-- foo True False
fooResult = foo myEqBool True False
#include <iostream> <br/>
<br/>
// class MyEq a <br/>
class MyEq<br/>
{ <br/>
public : <br/>
virtual ~MyEq ( ) throw ( ) { } <br/>
// void const *, <br/>
virtual bool unsafeMyEqual ( void const * x, void const * y ) const = 0 ;<br/>
virtual bool unsafeMyNotEqual ( void const * x, void const * y ) const = 0 ;<br/>
} ;<br/>
<br/>
// , <br/>
// <br/>
template < typename T > <br/>
class MyEqDictBase : public MyEq<br/>
{ <br/>
virtual bool unsafeMyEqual ( void const * x, void const * y ) const <br/>
{ return myEqual ( * static_cast < T const * > ( x ) , * static_cast < T const * > ( y ) ) ; } <br/>
virtual bool unsafeMyNotEqual ( void const * x, void const * y ) const <br/>
{ return myNotEqual ( * static_cast < T const * > ( x ) , * static_cast < T const * > ( y ) ) ; } <br/>
public : <br/>
virtual bool myEqual ( T const & x, T const & y ) const { return ! myNotEqual ( x, y ) ; } <br/>
virtual bool myNotEqual ( T const & x, T const & y ) const { return ! myEqual ( x, y ) ; } <br/>
} ;<br/>
<br/>
// . . <br/>
template < typename T > <br/>
class MyEqDict;<br/>
<br/>
// <br/>
template < typename T > <br/>
MyEqDict < T > makeMyEqDict ( ) { return MyEqDict < T > ( ) ; } <br/>
<br/>
// instance MyEq Bool <br/>
// MyEq bool <br/>
template <> <br/>
class MyEqDict < bool > : public MyEqDictBase < bool > <br/>
{ <br/>
public : <br/>
virtual bool myEqual ( bool const & l, bool const & r ) const { return l == r; } <br/>
} ;<br/>
<br/>
// <br/>
// , bool, Haskell' <br/>
bool fooDict ( MyEq const & dict, void const * x, void const * y ) <br/>
{ <br/>
return dict. unsafeMyNotEqual ( x, y ) ; // myNotEqual <br/>
} <br/>
<br/>
// <br/>
// foo :: (MyEq a) => a -> a -> Bool <br/>
template < typename T > <br/>
bool foo ( T const & x, T const & y ) <br/>
{ <br/>
return fooDict ( makeMyEqDict < T > ( ) , & x, & y ) ;<br/>
} <br/>
<br/>
int main ( ) <br/>
{ <br/>
std :: cout << foo ( true , false ) << std :: endl ; // 1 <br/>
std :: cout << foo ( false , false ) << std :: endl ; // 0 <br/>
return 0 ;<br/>
}
いくつかの標準クラスと構文糖
Enumは列挙です。 次/前の値、および数値による値を取得するための関数を定義します。
リストの構文シュガーで使用される
[ 1 .. 10 ]
、実際には、
enumFromTo 1 10
、
[ 1 , 3 .. 10 ] => enumFromThenTo 1 3 10
表示 -文字列への変換、
show :: a -> String
の主な機能。
たとえば、インタープリターが値を出力するために使用します。
読み取り -文字列からの変換、メイン関数
read :: String -> a
。
「汚れた」例外ではなく、「クリーン」な方法でエラーを通知するために、
Maybe a
(オプションの値)ではなく、値を返すことを選択した理由はわかりません。
Eq-比較、演算子
( == )
および
( /= )
(等号を消したような)
順序付き型、演算子
( < )
( > )
( <= )
( >= )
。 クラスEqの型メンバーシップが必要です。
さまざまなクラスのより完全なリストは、 ここにあります 。
ファンクター-ファンクター、
fmap :: ( a -> b ) -> fa -> fb
:(a-
fmap :: ( a -> b ) -> fa -> fb
関数。
明確にするために、この関数の使用例を示します。
つまり リストの場合は単なるghci> fmap (+1) [1,2,3]
[2,3,4]
ghci> fmap (+1) (Just 6)
Just 7
ghci> fmap (+1) Nothing
Nothing
ghci> fmap reverse getLine
hello
"olleh"
map
、オプションの値の場合関数
( + 1 )
が値自体である場合に適用され、入出力の場合はこの入出力の結果に関数が適用されます
I / Oについては以下で
getLine
しますが、
getLine
は文字列を返さないため、
reverse
を直接適用することはできません。
毎回新しく書き込まれたデータ型のインスタンスを指定することを避けるために、Haskellはいくつかのクラスに対してこれを自動的に行うことができます。
data Test a = NoValue | Test aa deriving ( Show , Read , Eq , Ord )
data Color = Red | Green | Yellow | Blue | Black | Write deriving ( Show , Read , Enum , Eq , Ord )
ghci> NoValue == ( Test 4 5 )
False
ghci> read "Test 5 6" :: Test Int
Test 5 6
ghci> ( Test 1 100 ) < ( Test 2 0 )
True
ghci> ( Test 2 100 ) < ( Test 2 0 )
False
ghci> [ Red .. Black ]
[ Red , Green , Yellow , Blue , Black ]
偉大で恐ろしいモナド
Monadクラスは「計算」です。つまり、 計算と結果を組み合わせる方法を説明できます。
すでに書かれているものよりも良い記事を書く可能性は低いので、これらのモナドが必要な理由を理解するために、最高の(私の意見では)記事へのリンクを提供します。
1. モナド -ロシア語のモナドに関するSPbHUGの記事と、おなじみの命令型言語での類推
2. IO inside-モナドを使用した入出力に関する英語の記事
3. さらにもう1つのHaskellチュートリアル -Haskellに関する本、 モナドのセクションでは 、モナドの本質であるComputationクラスの作成例について非常によく書かれています。
ここでは、後でのぞき見できるように非常に簡単に説明します。
次のそれぞれが前の計算の結果に依存する逐次的な計算を記述したいとします(何らかの不特定の方法で)。 これを行うには、適切なクラスを定義できます。このクラスには、少なくとも2つの関数が必要です。
最初の関数は基本的に何らかの値を取り、実行されると単純に同じ値を返す計算を返します。class Computation c where
return :: a -> ca
bind :: ca -> ( a -> cb ) -> cb
2番目の関数は2つの引数を取ります。
1.実行されると、タイプ
a
値を返す計算
2.タイプaの値を取り、タイプ
b
値を返す新しい計算を返す関数
結果は、タイプ
b
値を返す計算です。
なぜこれがすべて必要なのか、オプションの値の例を示します
いくつかの関数があり、それぞれが失敗してdata Maybe a = Just a | Nothing
Nothing
を返す場合があるとします。 次に、それらを直接使用すると、そのような読みにくいコードを取得する危険があります。
つまり これらの関数を単に順番に呼び出すのではなく、毎回値を確認する必要があります。funOnMaybes x =
case functionMayFail1 x of
Nothing -> Nothing -- ,
Just x1 -> -- , ,
case functionMayFail2 x1 of
Nothing -> Nothing -- ( "")
Just x2 -> --
しかし、この言語では、関数を引数として渡し、同じ方法で戻ることができます。
combineMaybe :: Maybe a -> ( a -> Maybe b ) -> Maybe b
combineMaybe Nothing _ = Nothing
combineMaybe ( Just x ) f = fx
combineMaybe
関数は、オプションの値と関数を受け入れ、この関数をオプションの値に適用した結果、または失敗を返します。
funOnMaybes
関数を書き換えます:
または、関数をインフィックスと呼ぶことができるという事実を使用して:funOnMaybes x = combineMaybe ( combineMaybe x functionMayFail1 ) functionMayFail2 --...
funOnMaybes x = x `combineMaybe` functionMayFail1 `combineMaybe` functionMayFail2 --...
関数
combineMaybe
のタイプが
bind
のタイプを正確に繰り返していることに気付くでしょう
combineMaybe
代わりに
Maybe
だけ
Maybe
あり
c
。
それがまさにモナドの定義instance Computation Maybe where
return x = Just x
bind Nothing f = Nothing
bind ( Just x ) f = fx
Maybe
ません。そこでは
bind
だけが呼び出され
( >>= )
、さらに前の計算の結果を使用しない追加の演算子
( >> )
があります。
さらに、モナドには構文糖が定義されているため、モナドの使用が大幅に簡素化されます。
funOnMaybes x = do
x1 <- functionMayFail1 x
x2 <- functionMayFail2 x1
if x2 == (0)
then return (0)
else do
x3 <- functionMayFail3 x2
return ( x1 + x3 )
else
内部の余分な
do
とその時の不在に注意して
do
。
do
は、複数の計算を1つに結合する単なる構文糖であり、
then
ブランチ
( return (0) )
には1つの計算があるため、そこでは必要ありません。
else
ブランチでは、計算は連続して2つあり、それらを結合するには、再び
do
使用する必要があり
do
。
戻る矢印
(<-)
した特別な構文は、非常に簡単に変換されます。
1. {e}-> eを実行します
1つの計算でこの計算自体があり、結合する必要はありません
2. {e; es}-> e >> do {es}
複数の連続した計算が演算子によって接続されています
( >> )
3. {宣言を許可する; es}-> do {es}で宣言を行う
doの中では、
let ... in
ような追加の宣言を行うことができます
4. {p <-e; es}-> ok p = do {es}; ok _ = eの「...」に失敗します>> = ok
最初の計算の結果が後で使用される場合、演算子
( >>= )
組み合わせに使用されます
後者の場合、
p
はサンプルであり、一致しない可能性があるため、このような構造が使用されます。
一致する場合、さらに計算が実行されます。一致しない場合は、文字列の説明を含むエラーが返されます。
fail
関数は、一般的にモナドの概念とは関係のない、モナドの別の追加関数です。
標準ライブラリには他にどのようなモナドインスタンスがありますか?
状態 -状態の計算。
State
内部デバイスを認識する
get/put
関数を使用して、状態を取得および設定できます。
import Control . Monad . State
fact' :: Int -> State Int Int -- - Int, - Int
fact' 0 = do
acc <- get --
return acc --
fact' n = do
acc <- get --
put ( acc * n ) -- n
fact' ( n - 1 ) --
fact :: Int -> Int
fact n = fst $ runState ( fact' n ) 1 -- - 1
runState
は、状態を持つ関数を計算し、結果と変更された状態を含むタプルを返します。 結果のみが必要なので、
fst
です。
リストもモナドです。 次の計算は、前の結果のすべてに適用されます。
dummyFun contents = do
l <- lines contents --
if length l < 3 then fail "" -- 3
else do
w <- words l --
return w --
ghci> dummyFun "line1\nword1 word2 word3\n \n \nline5"
["line1","word1","word2","word3","line5"]
Haskellの継続-モナド-Cont
継続は、 ロシアのwikiと英語のwikiで読むことができ、リンクをたどります。
それらは特別な注意に値しますが、私はすべてに適合するわけではなく、モナドとは直接関係がありません。
Schemeの継続に関する優れた記事は、ライブログでpalm_muteユーザーから入手できます。
I / Oもモナドを使用して実装されます。 たとえば、
getLine
関数のタイプは次の
getLine
です。
文字列を返すIOアクション。getLine :: IO String
IO
は次のように理解できます。
ここで、getLine :: World -> ( String , World )
World
は
World
の状態です
つまり 入出力関数は、いわば世界の状態を取得し、特定の結果と世界の新しい状態を返します。これはその後の関数で使用されます。
もちろん、これは単なる精神的な表現です。
リストやたぶんとは異なり、タイプ
IO
コンストラクターがないため、タイプ
IO String
結果をコンポーネントに解析することはできませんが、他の計算で使用するだけで、入出力の使用が確実に反映されます。関数のタイプ。
(「決して」-大声で言われますが、実際には
unsafePerformIO :: IO a -> a
がありますが、問題を理解し、絶対に必要な場合にのみ使用するのは安全ではありません。
言及する価値があるのはMonadトランスフォーマーです。
状態が必要な場合、I / Oが
IO
であれば
State
を使用できます。 しかし、関数がステートを持ちながらI / Oを実行したい場合はどうでしょうか?
この目的のために、 StateTトランスフォーマーが設計されており、
State
と別のモナドを接続します。 この他のモナドで計算を実行するには、
lift
関数が使用されます。
階乗の例を見てみましょう。これはバッテリーを印刷するように変更します
import Control . Monad . State
fact' :: Int -> StateT Int IO Int -- IO
fact' 0 = do
acc <- get
return acc
fact' n = do
acc <- get
lift $ print acc -- print acc - IO (), lift
put ( acc * n )
fact' ( n - 1 )
fact :: Int -> IO Int -- IO , :)
fact n = do
( r , _ ) <- runStateT ( fact' n ) 1
return r
ghci> fact 5
1
5
20
60
120
120
StateTに加えて、 ListT (リスト用)もあります。
モナドとトランスフォーマーモナドの完全なリスト。
便宜上、一般化された関数はモナド上で定義されます。 彼らの名前は自明であり、それらのほとんどはリスト関数を複製しているので、それらの一部をリストし、 このリンクを提供します
sequence :: Monad m => [ ma ] -> m [ a ]
--
mapM f = sequence . map f
forM = flip mapM
-- forM [1..10] $ \i -> print i
forever :: Monad m => ma -> mb -- ,
filterM :: Monad m => ( a -> m Bool ) -> [ a ] -> m [ a ] -- filter
foldM :: Monad m => ( a -> b -> ma ) -> a -> [ b ] -> ma -- foldl
when :: Monad m => Bool -> m () -> m () -- if else
リスト内包表記
(私は推定しないこの用語を翻訳する)
リスト内包表記を使用すると、数学表記に従ってリストを設計できます。
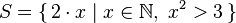
最後のリストがより頻繁に移動されることがわかります。ghci> take 5 $ [ 2 * x | x <- [ 1 .. ] , x ^ 2 > 3 ]
[ 4 , 6 , 8 , 10 , 12 ]
ghci> [ ( x , y ) | x <- [ 1 .. 3 ] , y <- [ 1 .. 3 ] ]
[ ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 2 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 1 ) , ( 3 , 2 ) , ( 3 , 3 ) ]
yはxに依存する場合があります。
ghci> [ x + y | x <- [ 1 .. 4 ] , y <- [ 1 .. x ] , even x ]
[ 3 , 4 , 5 , 6 , 7 , 8 ]
リストの内包表記も構文糖衣であり、次のように展開されます(最後の例)。
もちろん、それは直接展開されますが、リスト上のモナド計算とリスト内包表記との関係は非常に明白です。do
x <- [ 1 .. 4 ]
y <- [ 1 .. x ]
True <- return ( even x )
return ( x + y )
次回はすべての質問に答えようとしますが、チャットの実装を取り上げることができます(または、質問がほとんどない場合はすぐに)、すべての点で明確ではないかどうかを尋ねます。