
はじめに
この記事では、プロジェクト「絶対為替レート」の枠組みで実施された実験の結果について説明します。 リンクをクリックすると、実験プロトコルが表示されます。
プロジェクト「 絶対為替レート 」は、ペアの為替レートの分析、それらからの絶対為替レートの割り当て、およびそれらの分析に従事しています。 プロジェクトの枠組みの中で、ペアレートから絶対為替レートに変換する方法論が得られました。 このために、絶対通貨ABSが定義されています。 すべての通貨はABSに関連して引用されます。
この技術の詳細な説明は、「 通貨ペアから絶対為替レートへ 」という記事に記載されています 。
現在までに、絶対為替レート法の適用に関するいくつかの記事がすでに公開されています。 最後の2つを持ってきます。
記事「 絶対レートの相関による世界通貨の相互接続性の研究 」は、絶対為替レートの技術の応用の1つを説明しています。 異なる通貨間の関係を計算するための正式な方法が提供されます。
記事「 Markowitzが外国為替市場に適用したポートフォリオ手法 」では、外国為替ポートフォリオを最適化するための、これまでアクセスできなかった技術について説明しています。
以下では、ペア(相対)為替レートから絶対為替レートへの変換方法について説明します。 変換の数値パラメータとその計算方法が示されています。
ソースファイルでは、毎日の為替レートが毎日自動的にロードされ、絶対為替レートはそれらから計算されます。
変換マトリックスは2017年に取得されました。 復元されたペアレートの絶対からの偏差の誤差を最小化することにより、実際のペア交換レートで計算されました。 それ以降、最新のデータに対してエラー分析は実行されていません。
以下で説明する予期しない検証結果により、変換マトリックスを取得するための新しい手法が開発されました。 また、インポートされた見積の処理中にエラーが検出されました。
理論的根拠
絶対為替レートを取得するには、次の変換を行う必要があります。 開始するには、ペアのコースは対数です。 次に、それらに逆変換行列を掛けます。 最後に、指数を使用して対数スケールから戻ります。
ペアコースにさらに移行するには、絶対コースを記録する必要があります。 次に、直接変換行列を掛けます。 前と同じように指数を使用して結論付けます。
この技術の詳細については、「 通貨ペアから個々の通貨の絶対為替レートへ 」という記事で説明されています(2018年のこの記事のみが、この記事の表示とは対照的に、変換行列の転置表現を提供します)。
直接行列は簡単に決定できます。 その中の行は通貨に対応し、列は通貨ペアに対応します。 行列は非常にまばらで、ゼロ、1、およびマイナス1で構成されています。
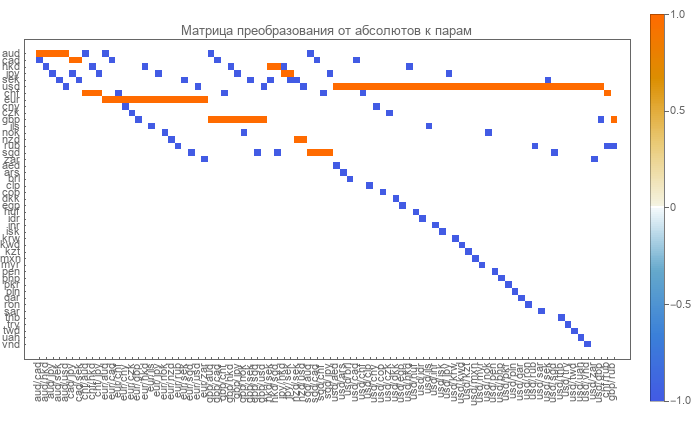
ゼロは、そのようなペアと通貨が存在しないことを示します。 単位は、ペアの分子の通貨に対応します。 マイナス1は、ペアの分母の通貨を示します。
ペアから絶対レートへの逆変換マトリックスは定義されていません。 計算する必要があります。 最も明白な方法は、ペア回復のエラーを最小限に抑えることです。 2017年にこのマトリックスを計算するために行われたもの。 この行列をグラフィカルに表現します。
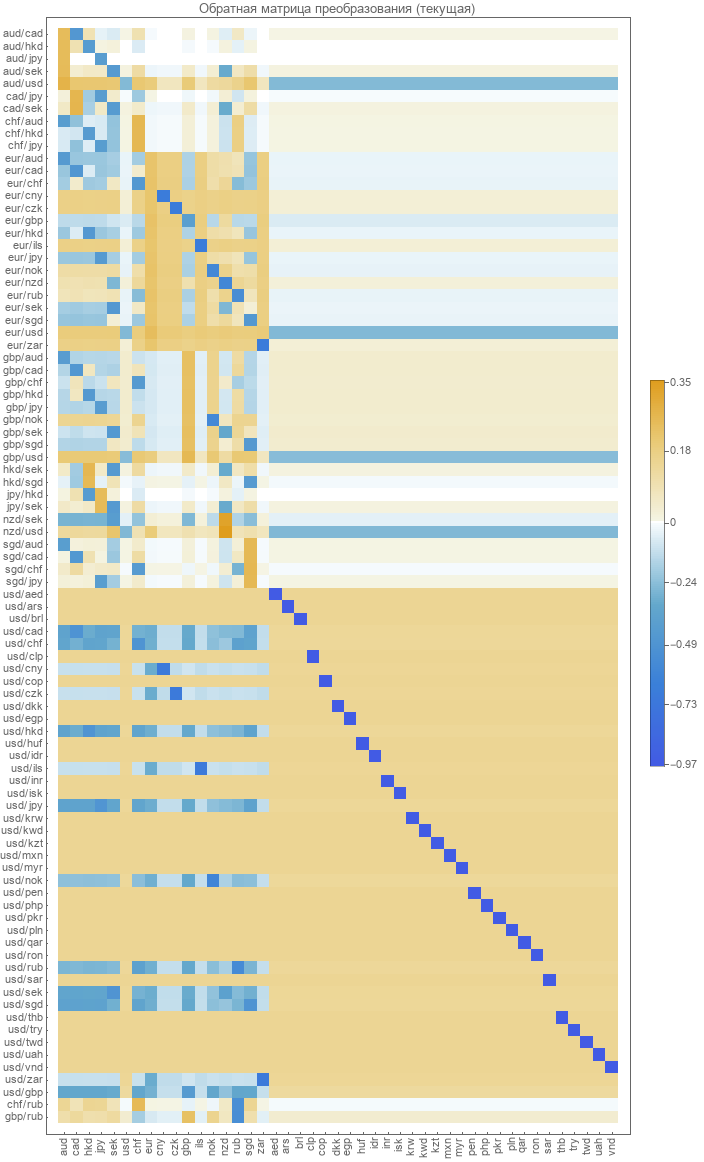
既存のモデルの精度を確認する
現在のマトリックスでは、絶対および復元ペアの為替レートが取得されました。 元のペアのコースと復元されたペアのコースの間には大きな違いがありました。

次に、すべてのペアの回復エラーの計算が実行されました。
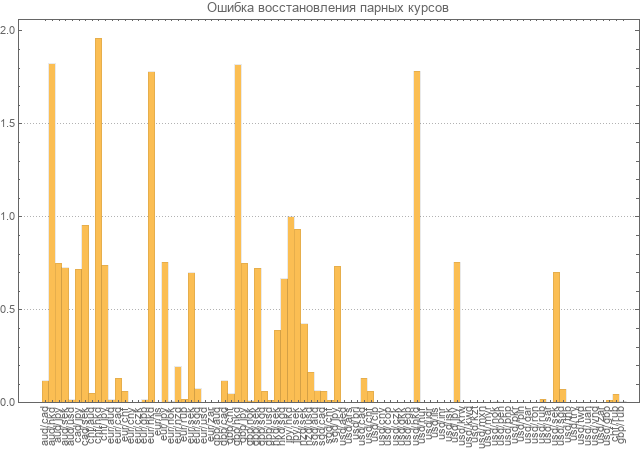
誤差は、モジュロで取られた相対偏差の平均と見なされました。 図からわかるように、多くのペアのエラーは値自体のほぼ2倍の大きさです。
もちろん、このレベルのエラーでは、モデルのサウンドを考慮することができず、再カウントが必要です。
ラインからの擬似逆行列
最初に試すことは、直接変換行列の逆行列を単純に計算することです。 マトリックスが非正方形であるという事実のため、 疑似逆変換を使用する必要があります。 結果は次のようになります。
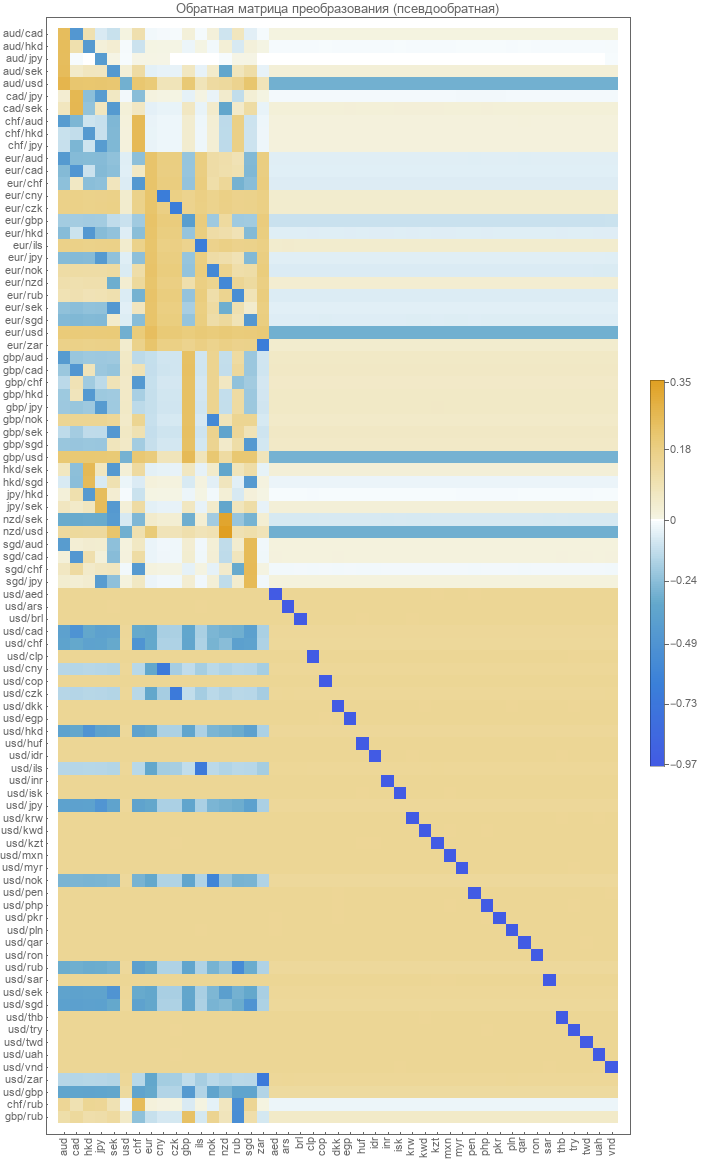
これは、最適化のために実際のペア為替レートを使用して以前に取得したものと非常に似ています。
絶対コースを計算します。 次に、絶対ペアコースから復元します。 エラーチャートは次のとおりです。

上記の評価のように、エラーも大きいことが判明しました。 このモデルも私たちに適していません。
線形独立成分による逆行列の計算
直接変換行列を詳細に分析すると、それが縮退した形式であることがわかります( 行列のランクは通貨行の数よりも少ない)。 つまり、直接行列には線形に依存する行があります。 したがって、許容可能な逆行列を取得することはできません。
この状況から抜け出すために、次の解決策が提案されました。 絶対コースからペアリングへの移行では、最初に線形独立コンポーネントに切り替える必要があります。 それからペアに移ります。 絶対コースからコンポーネントへ、およびコンポーネントからペアコースへの遷移の行列は非縮退であり、逆行列を取得できます。
線形独立成分を検索するには、ペアコースの単位行列を直接変換の行列に添付する必要があります。 したがって、絶対コースからペアへの遷移の2つのマトリックスと、ペアからペアへの遷移のアタッチされたマトリックスを取得します。

次に、この結合された行列の上部の段階的な形式への標準的な変換を実行します(実際、標準のWolfram Mathematica数学ツールはさらに対角形式になります )。 その結果、次の変換済みマトリックスを取得することができました。

この行列の列には、線形独立成分があります。 さらに、絶対コース(マトリックスの上部)とペアコース(結合された変換済みマトリックスの下部)の両方からそれらに切り替えることができます。
これらの遷移行列を線形独立コンポーネントに選び出します。 以下は、絶対コースからのコンポーネントの遷移マトリックスです。
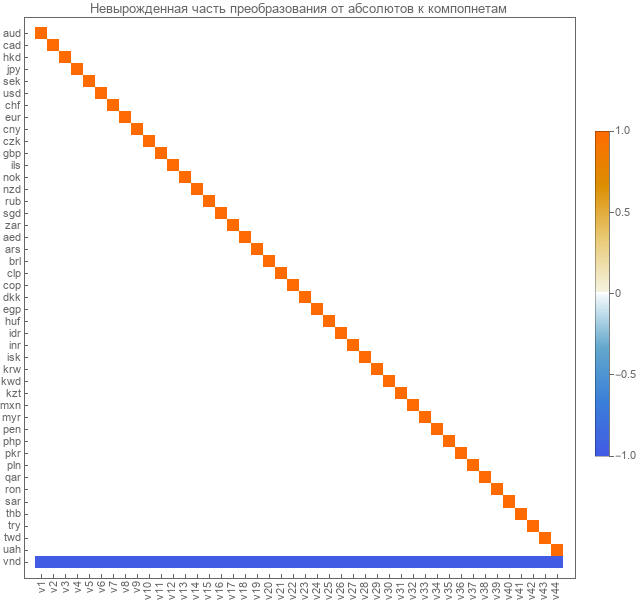
ペアコースから線形独立コンポーネントへの遷移マトリックスを次に示します。

絶対値からコンポーネントへの遷移は、上記で計算されたマトリックスを介して発生します。 逆行列を介してコンポーネントから絶対値への逆変換を行います。 非縮退であるという事実により、優れた逆行列が得られます。 疑似逆として受け取ります。 これが彼女の見解です。

これで、ペアから絶対値への完全な逆変換行列を取得できます。 これを行うには、ペアからコンポーネントへの変換行列に、コンポーネントから絶対値への逆変換行列を掛けます。 彼女はこんな感じ。

すでに上記と似ていますが、それでもマトリックスは異なります。 その結果を調べます。 絶対コースを計算し、それらからすでにペアのコースを復元します。 回復エラーは次のとおりです。

2つを除くすべてのペアで、ほぼゼロのエラー。 これらのペアの何が問題なのかを見つけます。
2つの通貨ペアで間違ったデータが受け入れられることがわかります。 jpy / hkdとjpy / sekの場合、データは10000個と100個になります。 修正して再確認する必要があります。
入力ペアコースを修正し(ロットを削除)、絶対ペアコースと復元されたペアコースを再計算した後、回復エラーを調べます。

0.3%以内にエラーが発生しました。 かなり許容できるレベルのエラー。
絶対的なコースチャートの例を次に示します。
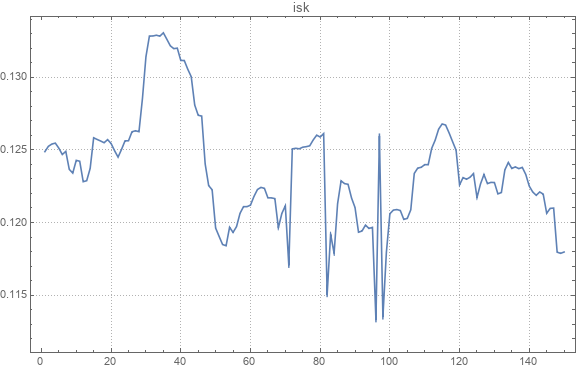
以下に、元のペアと復元されたペアの為替レートの例を示します。

逆変換の新しいマトリックスを再計算したため、すべての参加通貨の最新の絶対為替レートに関するデータを再度示します。
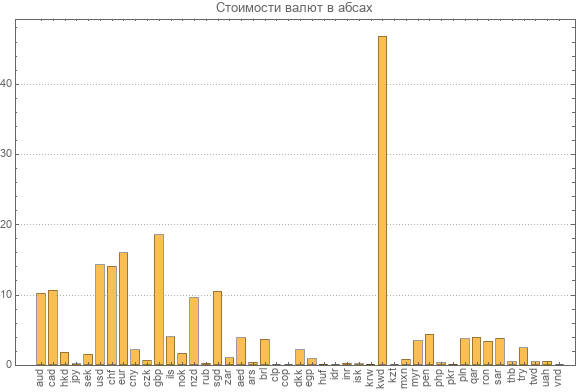
最も高価な通貨を見ることができます。 これはほぼ47腹筋の価値があるクウェートディナールです。 ベトナムドンの最小絶対値は0.003 absです。
結論
研究の結果、絶対レートを計算するための既存の方法は大きな誤差を与えることがわかった。 さらに、ソースデータでエラーが検出されました。
ペアから絶対値への逆変換マトリックスは、非縮退変換マトリックスを使用した少数の線形独立コンポーネントへの変換方法を使用してのみ取得されました。
逆変換行列を取得する方法は、ペアレートデータを使用しませんでした。 したがって、それらから独立しています。
実際のコースでの変換の検証では、低レベルのエラーが示されました。 そこから、見つかった逆変換のマトリックスは、対の為替レートから絶対レートに適用可能であると結論付けられました。
この方法は完全で数学的に検証されているとは主張していませんが、許容できる解決策として、絶対為替レートのさらなる研究に使用されます。