証明がすべてである数学では、事実も重要です。 ただし、事実は良好であり、モデルは良好であり、モデルの構築は信頼性の低いタスクです。 それでは、いくつの事実で十分でしょうか?

シーケンスの次の番号を見つけることができますか?
1、2、4、8
決定を下すためにさらにデータが必要な場合は、もう1つ数字を示します。
1、2、4、8、16
次の数字は32でなければなりませんか? パターンは明確です。次の番号を見つけるには、前の番号を2倍にする必要があります。 1×2 = 2; 2×2 = 4; 4×2 = 8; 8×2 = 16だから、次の数は16×2 = 32になるはずです。これを確認するには、さらに多くの事実が必要ですか?
しかし、次の数字が32であると仮定するのは合理的ですが、これは必ずしも真実ではありません。 次のシーケンスを考えてみましょう。円上にあるポイントを結ぶ線で円を分割するセクションの数をカウントします。
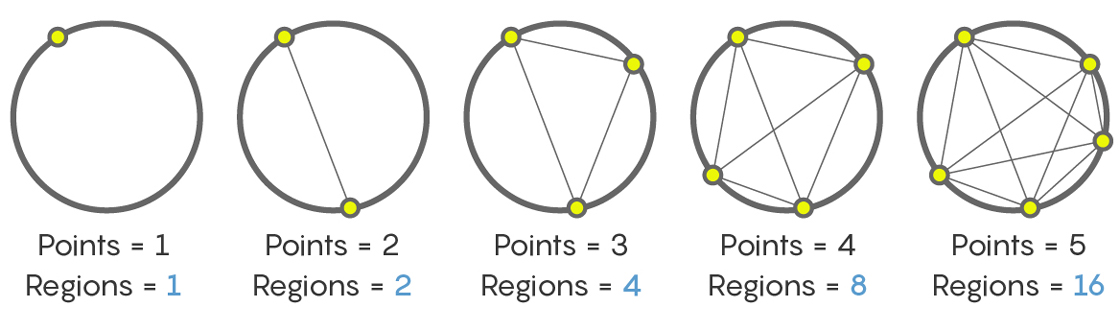
1つのポイントが1つのセクション(円の内部全体)を提供します。 2つのポイント-2つのセクション。 3つのポイント-4つのセクション。 5と6はそれぞれ8と16です。 結果はシーケンスです
1、2、4、8、16
また、円上の6点の線を接続すると、いくつのセクションが表示されますか? あなたが、この仕事に初めて直面する多くの人々のように、32と言うならば、誰もあなたを非難しません。しかし、これはそうではありません。 実際、どれほど面倒な場合でも、答えは31になります。 自分を数えて、もう一度確認してください。
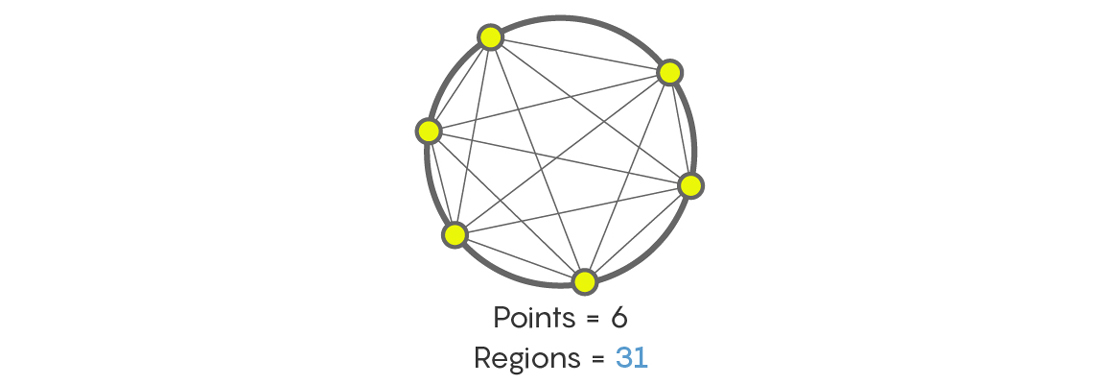
もちろん、毎回倍増する数字から、1、2、4、8、16、32、64などのようなシーケンスがあります。 しかし、他のシーケンスもあります。たとえば、円上のポイントを結ぶ線で円を分割するセクションの最大数は1、2、4、8、16、31、57、99などです。 シーケンス1、2、4、8、16を満たすと、次の数字は32になるという事実はすべてあると思うかもしれませんが、何か他のものがあるかもしれません。
数学には、私たちの期待に挑戦し、想像力を働かせるという長い伝統があります。 したがって、数学者は、事実だけでなく、厳密な証明を得るように常に努力しています。 証明は数学的な真実を確立します。 すべての事実は、シーケンスの次の数字として32を指している可能性がありますが、厳密な証拠がなければ、それを確認することはできません。
それでも、数学者にとっての事実は有用で重要です。 何かを証明する前に、私たちはしばしば利用可能な情報で遊び、問題を研究し、例を検討し、データを収集します。 私たちは事実を研究し、重さを量り、次に何をすべきかを決定します。 これらの結果は私たちの意見を形成し、いくつかの定理を証明し、他の定理に反論することを提案します。
双子素数仮説は、事実が証明と同じように数学的思考を制御する一例です。 双子の素数は2だけ異なる素数のペアです。たとえば、3と5、11と13、101と103です。双子の素数の仮説は、そのような双子の最大のペアがないことを示唆しています。無限に移動すると、ペアは数直線上に常に表示されます。
双子素数仮説は定理ではありません。なぜなら、これが数論で最も有名な問題の1つであるという事実にもかかわらず、誰もまだそれを証明できていないからです。 しかし、サポートには多くの事実があるため、ほとんどの人がそれが真実だと信じています。
たとえば、素数の検索では、双子素数の非常に大きなペアが常に見つかります。 最大の既知のペアの各素数には、それぞれ400,000桁が含まれています。 この仮説に類似した定理も証明されています。 2013年、 Zhang Ethanは、数千万を超えない数の素数のペアが無限に存在することを証明することで、数学的コミュニティに衝撃を与えました。 後に続くオープンなPolymathプロジェクトのおかげで、差が246を超えない素数のペアが無限にあることがわかります。 2だけ異なる素数のペアが無限に存在することはまだ証明されていませんが、それでも2は無限に246よりも246にはるかに近いです。
これらおよびその他の理由から、正義の信念は、たとえ仮説が証明されていなくても、あまり物議をかもしていません。 ただし、より論争の的となる情報に基づいた意見を構築するために事実を使用する数学の他の領域があります。
楕円曲線の研究では、そのランクは、大まかに言って、この曲線を解く複雑さの数値推定を示します。 長年、楕円曲線のランクは制限されていないと考えられていました。つまり、 曲線のランクの値や解の複雑さに制限はありません。
ただし、最近の研究により、数学者はランクが制限される可能性について考えています。 この論文は、ランクが21を超える曲線が有限数存在する可能性があるという証拠を示しています。
ただし、注意が必要です。 数学者によって収集された事実は楕円曲線の世界から取られたものではありません-それらは研究者が曲線をモデル化するために使用した行列に関連しています。 数学モデルは科学で広く使用されており、数学自体を研究するために内側に向けることさえできます。 これらは非常に強力なツールであり、理解できないタスクを、私たちが対処しやすいものに置き換えることができます。
しかし、モデルの使用は難しい作業です。 モデルが私たちが理解しようとしているものと非常によく似ていることを決して確信できないので、その動作から結論を引き出すことができます。 また、私たちのモデルが最も重要な場所で正確に類似していることを確信することはできません。 したがって、モデルに基づいて収集した事実が、研究している現象の実際の特性を本当に証明していることを確認することは困難です。 これらの問題を、単純な仮説の単純なモデルに基づいて調べてみましょう。
次の文を検討したいと想像してください。2つの線は交差するか平行です。
交差とは、直線間の共通点の存在を意味し、平行とは、それらが一方向に進むが交差しないという事実を意味します(この概念は別の方法で定義できますが、簡単にするためにこれを使用します)。
この問題を調査するには、モデルを作成します。 各線は斜線の方程式で表されますが、これは学校のコースで覚えることができます。 つまり、各行は次の形式の方程式で記述できると仮定します。
y = mx + b
ここで、mは線の勾配(急峻性)、bはy軸(垂直軸)の交点です。
この方法で線をモデル化すると、それらの実験に便利です。 このモデルでは、mとbの乱数のペアを選択して、ランダムな線を作成できます。 ランダムな線のペアを選択してチェックできます-それらは交差しますか? 彼らは一方通行ですか? 他に何か起こっていますか?
そのような実験の結果がどのように見えるかの例をいくつか示します。
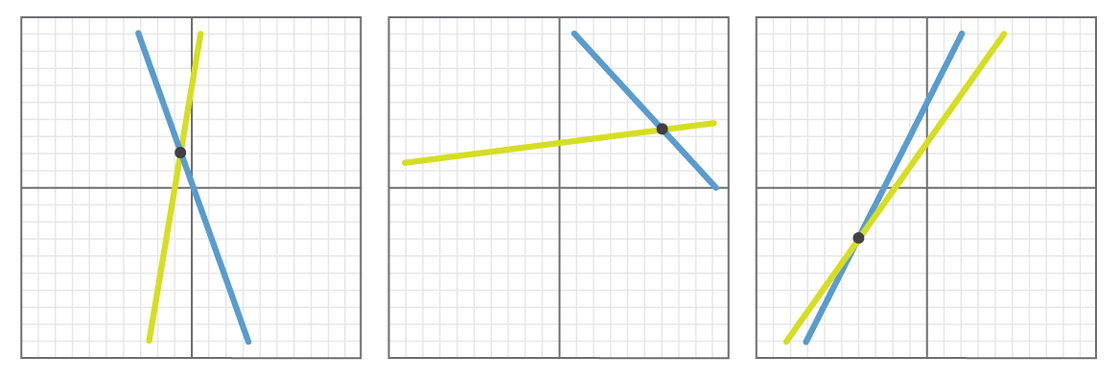
各例では、ランダムに選択された線が交差しています。 この実験を1,000回、または10,000、または100万回行うと、すべての場合に線が交差または平行になることがわかります(2本の線が同じ勾配を持っている可能性は低いため、すべての線が交差する可能性が高いです)偶然)。
したがって、100万の例を見てみると、仮説が本当である可能性が最も高いという結論に達することができます。 すべての事実は、線のペアが平行または交差するというステートメントを完全にサポートしています。
ただし、事実はモデルが優れているだけであり、モデリングは危険です。 この例では、自分自身にどのような危険が生じたかを見てみましょう。
1つの問題は、特定の種類の線が他の線よりも一般的であることです。 以下は、b = 0および0≤m≤1の50本の線を示すグラフです。
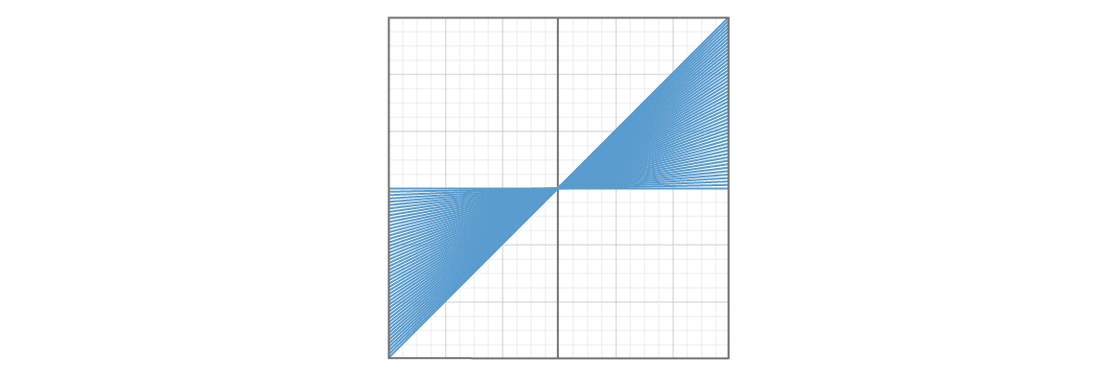
そして、b = 0かつm≥1の50本の線を示すグラフです。

平面の4分の1が0〜1の傾きの直線で覆われているように見え、別の4分の1が1より大きい傾きの直線で覆われているように見えます。飛行機の2番目のセクションになります。 これは、勾配が0から1の特定の線がモデルでほとんど表示されないことを意味します。 そして、直線のある平面のこの部分で奇妙なことが起こった場合、我々のモデルはこれについて教えてくれないでしょう。
2番目のチャートをよく見ると、別の問題があります。 mが大きくなるほど、直線はより急勾配になります。 最もクールな直線は垂直です。 垂直線の勾配は何ですか? 定義では、定義されていません。垂直線を説明できるようなmはありません。 モデルには垂直線がないため、実験することはできません。 事実の収集をまだ開始していませんが、モデル構築スキームのために、いくつかの特別なケースをすでに除外しています。
同じことが、モデルの最も深刻な問題にも関係しています。 3次元空間を簡単に想像できる人は、おそらく私たちの仮説が間違っていることにすぐに気づいたでしょう。 直線は交差または平行である必要はありません。 建物の異なる階で2つの廊下が異なる方向に進むと想像してください。 これらは交差する直線です-交差せず、平行ではない直線。
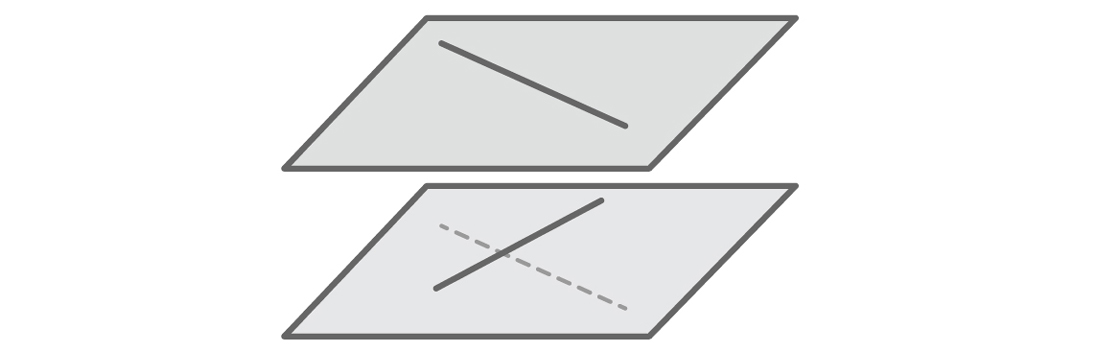
交差線は異なる平面になければなりません。 しかし、モデルは方程式y = mx + bを介して任意の線を定義するため、すべての線が同じ平面にあると自動的に想像しました。 モデルは、2つの線が同じ平面にある場合、実際に交差するか平行になる必要があるため、仮説をサポートするファクトのみを提供します。 他の事実は表示されません。モデルには交差する線はありません。 縦線の場合のように、モデルは想像できないものを除外しました。
これは、無限のセットから乱数を選択する手順など、トリッキーな質問を含む一連の問題を持つ愚かなモデルを使用した簡単な例です。 楕円曲線のランクを研究する専門の数学者は、そのような単純化された明らかな間違いを決して犯さなかっただろう。
これらの数学者は、モデルを扱う際に注意すべきことを知っています。 彼らは、モデルがどれほど有用で興味深いものであるか、または収集された事実がどれほど説得力があるかに関わらず、楕円曲線が彼らが想像しなかった特性を明らかにするかもしれないことを知っています。 これが想像できない場合、モデルはこれを考慮に入れないため、事実は反映されません。
しかし、新しいモデルが正しいかどうかに関係なく、数学者は楕円曲線について生産的に考えるようになりました。 それが本当に真実を反映している場合、マトリックスの世界からのアイデアは曲線の挙動を説明できます。 そうでない場合、なぜ楕円曲線をこのようにモデル化できないのかを理解することは、問題をよりよく理解することにつながります。 収集した事実は、何らかの形で証明に近づけることができます。