ラフスケッチの写真：NVIDIA GauGANニューラルネットワークはどのように正確に機能しますか

先月、NVIDIA GTC 2019で、NVIDIAは、ユーザーが描いたシンプルな色のボールを、見事な写真のようにリアルな画像に変える新しいアプリケーションを発表しました。





このアプリケーションは、ディープラーニングに基づいた生成的競合ネットワーク （GAN）の技術に基づいて構築されています。 NVIDIA自体はそれをGauGANと呼んでいます-これは、アーティストのPaul Gauguinを指すことを意図したしゃれです。 GauGAN機能は、新しいSPADEアルゴリズムに基づいています。



この記事では、このエンジニアリングの傑作がどのように機能するかを説明します。 そして、できるだけ多くの興味のある読者を引き付けるために、畳み込みニューラルネットワークがどのように機能するかについて詳細に説明しようとします。 SPADEは生成競争ネットワークであるため、それらについて詳しく説明します。 ただし、この用語に既に精通している場合は、すぐに「画像から画像へのブロードキャスト」セクションに進むことができます。

画像生成

理解を始めましょう。最新の深層学習アプリケーションのほとんどは、神経判別型（識別器）を使用し、SPADEは生成ニューラルネットワーク（ジェネレーター）です。

弁別器

弁別器は入力データを分類します。 たとえば、画像分類子は、画像を取得して1つの適切なクラスラベルを選択する弁別器です。たとえば、画像を「犬」、「車」、「交通信号灯」として定義します。 分類器によって取得された出力は、通常、数値のベクトルとして表されます $$$v$ どこで $$$v_i$ 画像が選択されたものに属するというネットワークの信頼度を表す0〜1の数値 $$$i$ クラス。



識別器は分類のリストを作成することもできます。 彼は、画像の各ピクセルを「人」または「機械」のクラスに分類することができます（いわゆる「セマンティックセグメンテーション」）。





分類器は、3つのチャネル（赤、緑、青）を持つ画像を取得し、画像が表すことができる各可能なクラスの信頼ベクトルと比較します。



画像とそのクラスの間の接続は非常に複雑であるため、ニューラルネットワークは多くのレイヤーのスタックを通過し、各レイヤーはそれを「わずかに」処理し、その出力を次の解釈レベルに渡します。

発電機

SPADEなどの生成ネットワークは、データセットを受け取り、このデータクラスに属しているかのように見える新しい元のデータを作成しようとします。 同時に、データは何でもかまいません：音、言語、またはその他のものですが、画像に焦点を合わせます。 一般に、このようなネットワークへのデータ入力は、単に乱数のベクトルであり、入力データの可能なセットのそれぞれが独自の画像を作成します。





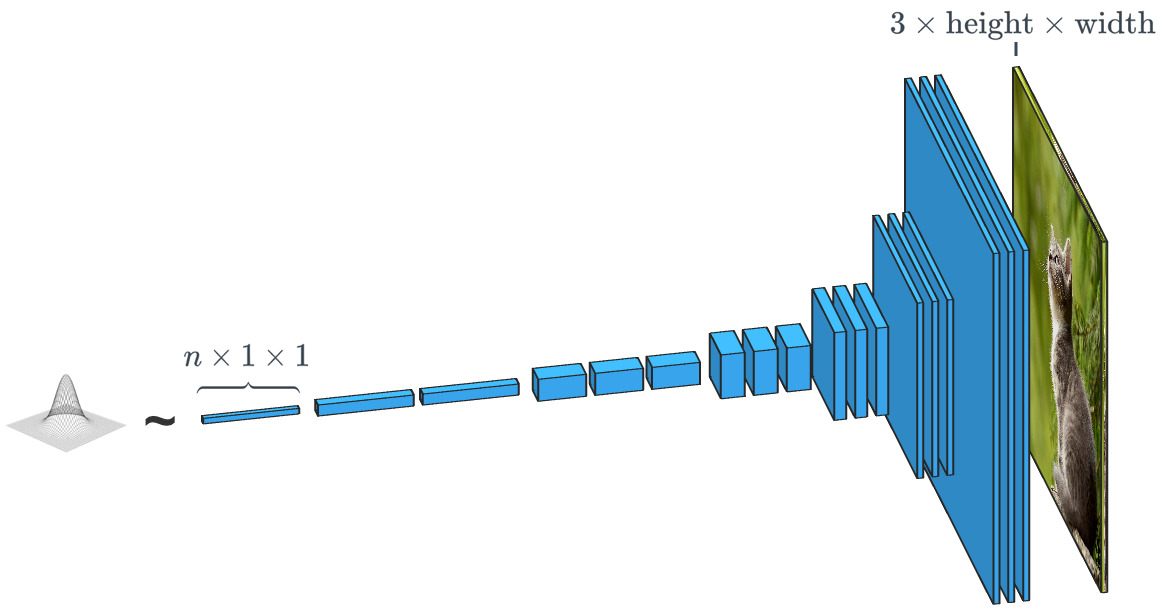
ランダムな入力ベクトルに基づくジェネレーターは、画像分類器とは実質的に反対に機能します。 「条件付きクラス」ジェネレーターでは、入力ベクトルは実際にはデータクラス全体のベクトルです。



これまで見てきたように、SPADEは単なる「ランダムベクトル」以上のものを使用します。 システムは、「セグメンテーションマップ」と呼ばれる一種の図面によって導かれます。 後者は、何をどこに投稿するかを示します。 SPADEは、前述のセマンティックセグメンテーションとは逆のプロセスを実行します。 一般に、あるタイプのデータを別のタイプのデータに変換する差別的なタスクには同様のタスクがありますが、それは別の異常なパスを取ります。



現代のジェネレーターとディスクリミネーターは通常、畳み込みネットワークを使用してデータを処理します。 畳み込みニューラルネットワーク（CNN）の詳細については、 Chew on KarnaまたはAndrei Karpatiの記事を参照してください。



分類器とイメージジェネレーターの間には1つの重要な違いがあり、処理中にイメージのサイズがどれだけ正確に変化するかにあります。 画像がすべての空間情報を失い、クラスのみが残るまで、画像分類子はそれを減らす必要があります。 これは、レイヤーを組み合わせたり、個々のピクセルを通過させるたたみ込みネットワークを使用することで実現できます。 一方、ジェネレーターは、畳み込み転置と呼ばれる「畳み込み」とは逆のプロセスを使用して画像を作成します。 彼はしばしば「デコンボリューション」または「逆コンボリューション」と混同されます。





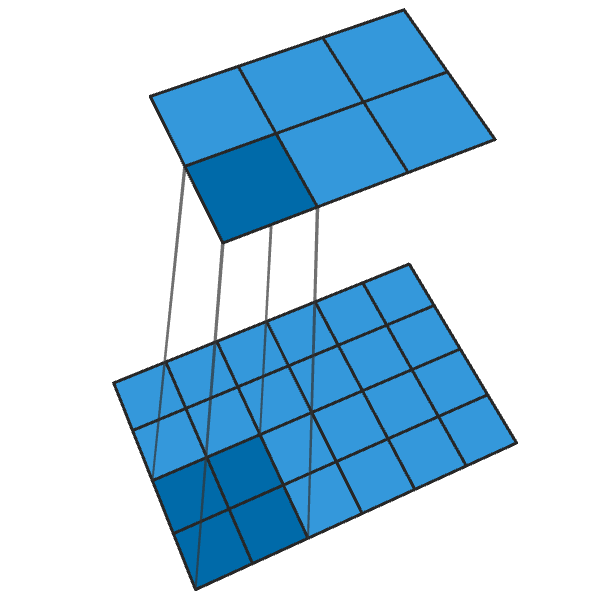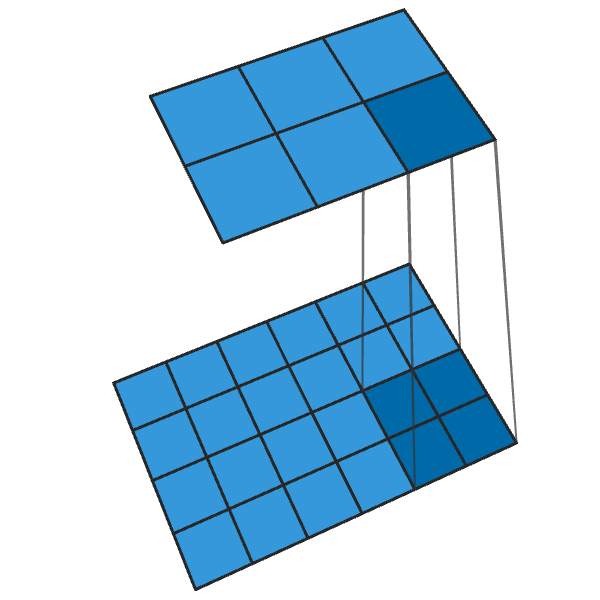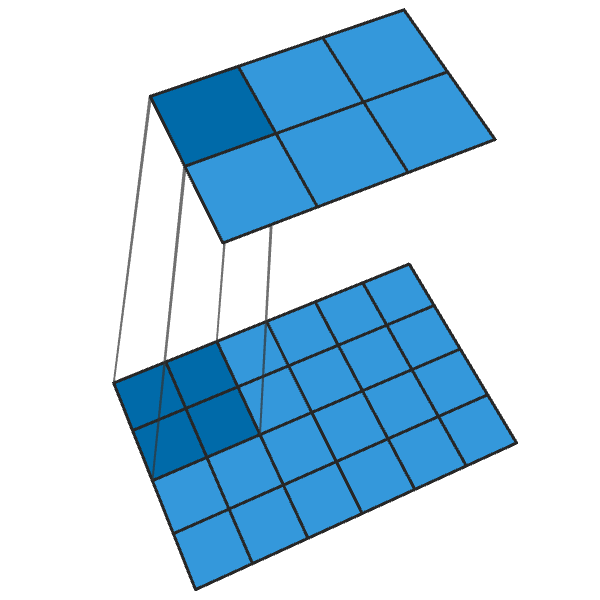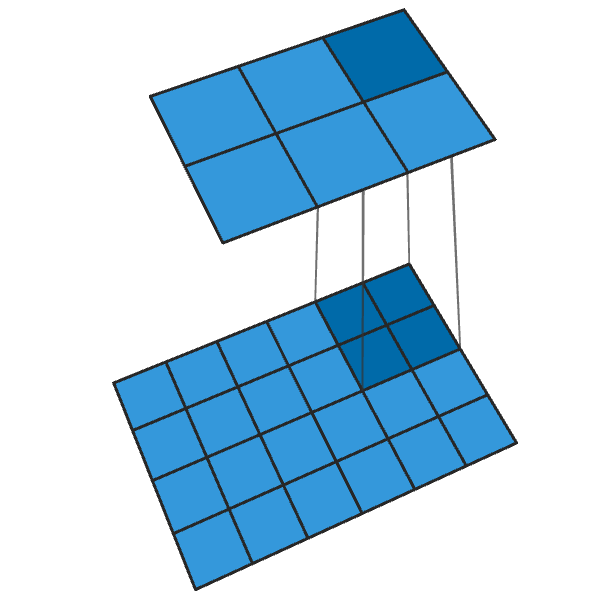
「2」ステップの従来の2x2コンボリューションは、各2x2ブロックを1ポイントに変換し、出力サイズを1/2に縮小します。





ステップが「2」の転置された2x2コンボリューションは、各ポイントから2x2ブロックを生成し、出力サイズを2倍にします。

発電機トレーニング

理論的には、畳み込みニューラルネットワークは上記のように画像を生成できます。 しかし、どのように彼女を訓練しますか？ つまり、入力画像データのセットを考慮する場合、ジェネレーター（この場合はSPADE）のパラメーターを調整して、提案されたデータセットに対応するように見える新しい画像を作成するにはどうすればよいですか？



これを行うには、それぞれが正しいクラスラベルを持つ画像分類子と比較する必要があります。 ネットワーク予測ベクトルと正しいクラスがわかれば、逆伝播アルゴリズムを使用してネットワーク更新パラメーターを決定できます。 これは、目的のクラスを決定する際の精度を高め、他のクラスの影響を減らすために必要です。





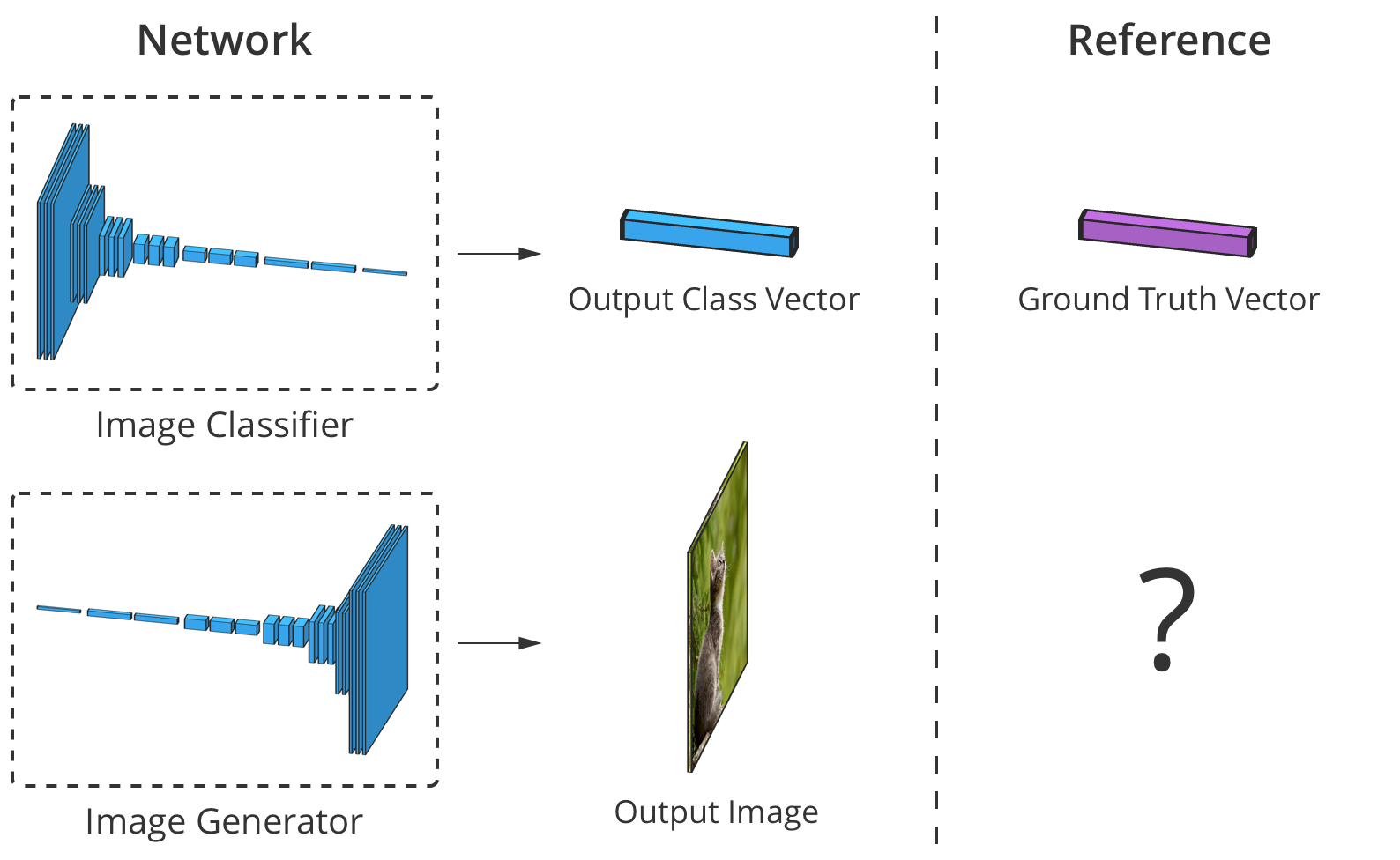
画像分類器の精度は、要素ごとにその出力要素を正しいクラスベクトルと比較することで推定できます。 ただし、ジェネレーターには「正しい」出力イメージはありません。



問題は、ジェネレーターが画像を作成するとき、各ピクセルに「正しい」値がないことです（事前に準備されたベース、約Trans。に基づく分類器の場合のように、結果を比較することはできません）。 理論的には、そのピクセル値が実際の画像と非常に異なっていても、信じられてターゲットデータに似ている画像はすべて有効です。



それでは、どのピクセルで出力を変更する必要があるのか​​、どのようにしてより現実的な画像を作成できるのか（つまり、「エラー信号」を与える方法）ジェネレーターにどのように伝えることができますか？ 研究者はこの質問をよく考えており、実際、それは非常に困難です。 実際の画像から平均「距離」を計算するなど、ほとんどのアイデアでは、ぼやけた低品質の画像が生成されます。



理想的には、「このイメージと実際のイメージを区別するのはどれくらい難しいか」などの「高レベル」の概念を使用して、生成されたイメージがどの程度現実的であるかを「測定」できます。

生成的敵対ネットワーク

これは、まさにGoodfellow et al。、2014の一部として実装されたものです。 アイデアは、1つではなく2つのニューラルネットワークを使用して画像を生成することです。1つのネットワーク-

ジェネレータ、2番目は画像分類器（弁別器）です。 弁別器のタスクは、ジェネレーターの出力画像をプライマリデータセットの実画像と区別することです（これらの画像のクラスは「偽」および「実」として指定されます）。 ジェネレーターの仕事は、データセット内の画像に可能な限り類似した画像を作成することにより、弁別器をだますことです。 このプロセスでは、ジェネレータとディスクリミネータが敵であると言えます。 したがって、名前： ジェネレーティブ-敵対的ネットワーク 。





ランダムなベクトル入力に基づく生成的競合ネットワーク。 この例では、ジェネレーター出力の1つは、識別器をだまして「実際の」画像を選択させようとしています。



これはどのように役立ちますか？ これで、0（「false」）から1（「real」）までの値である、判別子の予測のみに基づいたエラーメッセージを使用できます。 弁別器はニューラルネットワークであるため、エラーに関する結論を画像ジェネレーターで共有できます。 つまり、識別器は、識別器をより「欺く」ために画像をどこでどのように調整する必要があるか（つまり、画像のリアリズムを高める方法）をジェネレーターに伝えることができます。



偽の画像を見つける方法を学習する過程で、弁別器はジェネレーターに作業を改善する方法についてより良いフィードバックをジェネレーターに与えます。 したがって、弁別器は、ジェネレーターに対して「損失の学習」機能を実行します。

栄光の小さなGAN

作業中に当社が検討したGANは、上記のロジックに従います。 彼の差別者 $$$D$ 画像を分析します $$$x$ そして値を取得します $$$D（x）$ 0から1まで。これは、イメージが本物であるか、ジェネレーターによって偽造されているという彼の信頼度を反映しています。 彼の発電機 $$$G$ 正規分布数のランダムなベクトルを取得します $$$Z$ 画像を表示します $$$G（z）$ それは弁別者によってだまされる可能性があります（実際、この画像 $$$D（G（z））$ ）



議論しなかった問題の1つは、GANのトレーニング方法と、ネットワークパフォーマンスの測定に開発者が使用する損失関数です。 一般に、損失関数は、識別器が学習するにつれて増加し、発生器が学習するにつれて減少するはずです。 ソースGANの損失関数は、次の2つのパラメーターを使用しました。 最初は

弁別器が実際の画像を実際に正しく分類する度合いを表します。 2番目は、弁別器が偽の画像をどれだけうまく検出できるかです。



$$ $ inline $ \ begin {equation *} \ mathcal {L} _ \ text {GAN}（D、G）= \ underbrace {E _ {\ vec {x} \ sim p_ \ text {data}} [\ log D（ \ vec {x}）]} _ {\ text {実画像の精度}} + \下括弧{E _ {\ vec {z} \ sim \ mathcal {N}} [\ log（1-D（G（\ vec {z}））]} _ {\ text {偽物の精度}} \ end {equation *} $ inline $



弁別器 $$$D$ 画像が本物であるという彼の主張を導き出します。 それは理にかなっています $$$LogD（x）$ 弁別者がxを実数と見なすと増加します。 弁別器が偽の画像をよりよく検出すると、式の値も増加します。 $$$ログ（1-D（G（z））$ （1を目指して努力し始める） $$$D（G（z））$ 0になる傾向があります。



実際には、画像のバッチ全体を使用して精度を評価します。 私たちは多くの（しかし、決してすべてではない）実際の画像を撮ります $$$x$ そして、多くのランダムなベクトル $$$Z$ 上記の式に従って平均値を取得します。 次に、一般的なエラーとデータセットを選択します。



時間が経つにつれて、これは興味深い結果につながります。



MNIST、TFD、およびCIFAR-10データセットをシミュレートするGoodfellow GAN。 輪郭画像は、データセット内で隣接する偽物に最も近い画像です。



これはすべて、わずか4.5年前には素晴らしいものでした。 幸い、SPADEや他のネットワークが示すように、機械学習は急速に進歩を続けています。

トレーニングの問題

生成競争ネットワークは、準備の複雑さと作業の不安定性で有名です。 問題の1つは、トレーニングのペースで発電機が識別器よりもはるかに先にある場合、画像の選択が識別器を欺くのに役立つものに限定されることです。 実際、結果として、発電機のトレーニングは、弁別器をtrickすための単一の普遍的なイメージを作成することになります。 この問題は「崩壊モード」と呼ばれます。





GAN折りたたみモードはGoodfellowのモードに似ています。 これらの寝室の画像の多くは互いに非常に似ていることに注意してください。 出所



別の問題は、発電機が効果的に弁別器をだますとき $$$D（g（Z））$ 、非常に小さな勾配で動作するため、 $$$\ mathcal {L} _ \ text {GAN} G（\ vec {z}）$ この画像がより現実的に見える真の答えを見つけるのに十分なデータを取得できません。



これらの問題を解決するための研究者の努力は、主に損失関数の構造を変更することを目的としていました。 Xudong Mao et al。、2016によって提案された単純な変更の1つは、損失関数の置き換えです $$$\ mathcal {L} _ \ text {GAN}$ いくつかの単純な関数 $$$V_ \ text {LSGAN}$ 、より小さい面積の正方形に基づいています。 これにより、トレーニングプロセスが安定し、減衰のない勾配を使用してより良い画像と崩壊の可能性が低くなります。



研究者が遭遇した別の問題は、高解像度の画像を取得することの難しさです。これは、部分的に詳細な画像は、偽造画像を検出するためにより多くの情報を弁別者に与えるためです。 最新のGANは、低解像度の画像でネットワークのトレーニングを開始し、目的の画像サイズに達するまで徐々にレイヤーを追加します。





GANトレーニング中に高解像度のレイヤーを徐々に追加すると、プロセス全体の安定性が大幅に向上し、結果として得られる画像の速度と品質が大幅に向上します。

画像間ブロードキャスト

これまで、入力データのランダムなセットから画像を生成する方法について説明してきました。 しかし、SPADEはランダムデータを使用するだけではありません。 このネットワークは、セグメンテーションマップと呼ばれる画像を使用します。マテリアルクラスを各ピクセル（草、木、水、石、空など）に割り当てます。 この画像から、カードはスペードであり、写真のように見えるものを生成します。 これは「画像間ブロードキャスト」と呼ばれます。





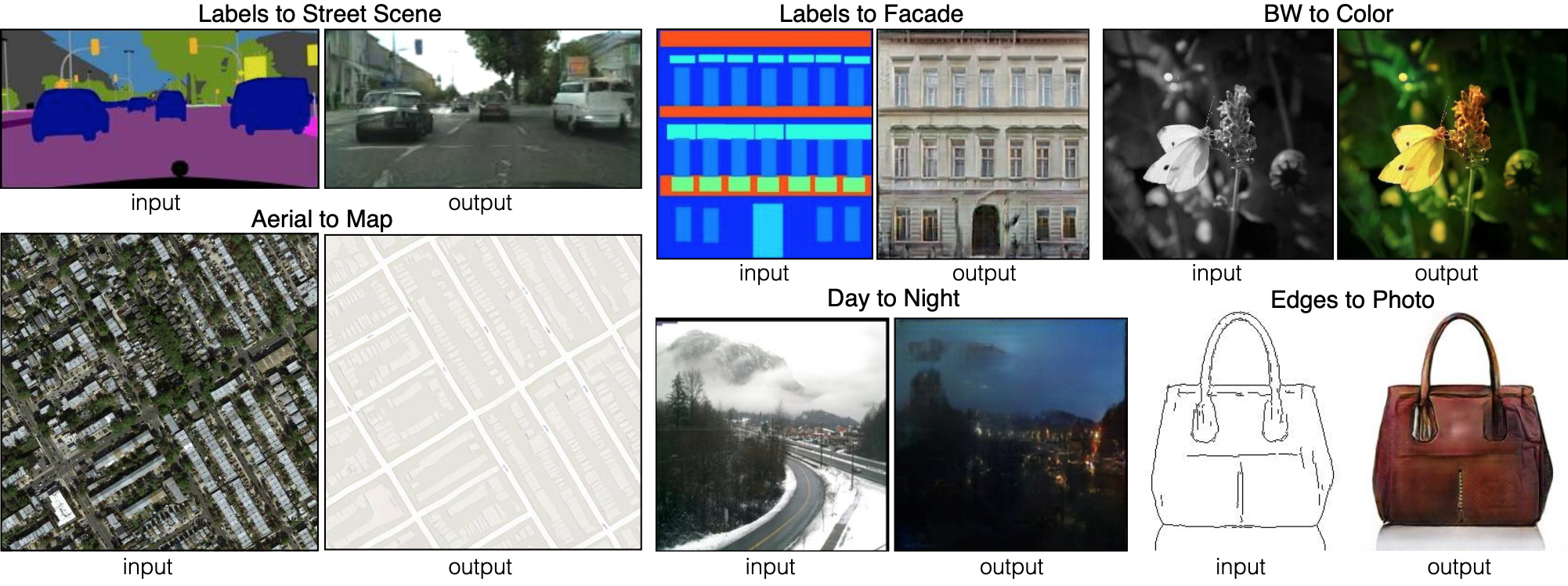
pix2pixが示す6種類の画像間ブロードキャスト。 Pix2pixは2つのネットワークの前身です。これについては、pix2pixHDとSPADEでさらに説明します。



ジェネレーターがこのアプローチを学習するには、セグメンテーションマップと対応する写真のセットが必要です。 GANアーキテクチャを変更して、ジェネレーターとディスクリミネーターの両方がセグメンテーションマップを受け取るようにします。 もちろん、ジェネレーターは「どの方法で描画するか」を知るためにマップを必要とします。 識別器は、ジェネレーターが適切な場所に適切なものを配置することを確認するためにも必要です。



トレーニング中、ジェネレーターはセグメンテーションマップ上で「空」が示されている場所に芝生を置かないことを学習します。そうしないと、識別器が偽の画像などを簡単に検出できるためです。





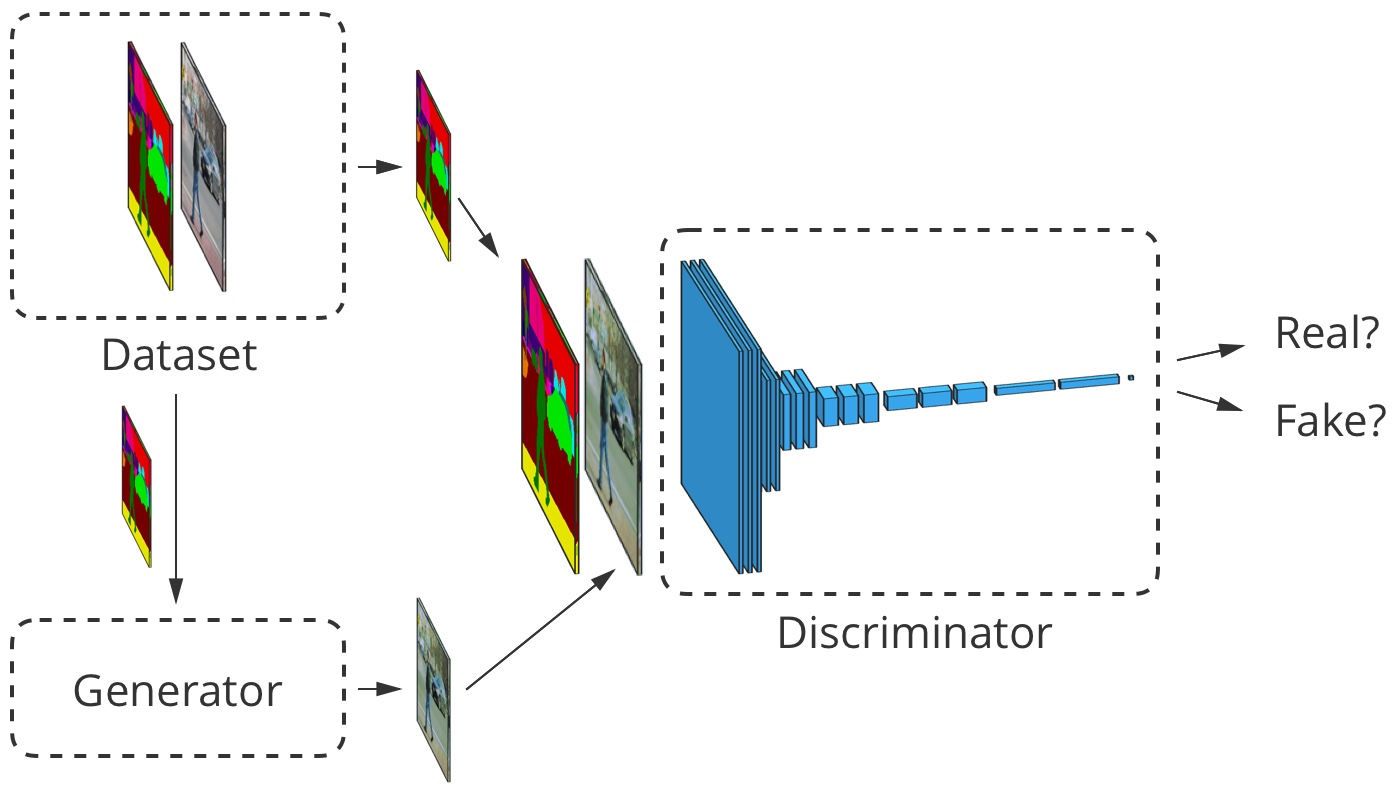
画像から画像への変換の場合、入力画像はジェネレーターとディスクリミネーターの両方で受け入れられます。 弁別器はさらに、トレーニングデータセットからジェネレーター出力または真の出力を受け取ります。 例

画像から画像へのトランスレーター開発

実際の画像から画像へのトランスレータpix2pixHDを見てみましょう。 ちなみに、SPADEは、pix2pixHDの画像と類似性のほとんどの部分のために設計されました。



イメージからイメージへのトランスレーターの場合、ジェネレーターはイメージを作成し、入力として受け入れます。 畳み込みレイヤーマップを使用することもできますが、畳み込みレイヤーは小さな領域でのみ値を結合するため、高解像度の画像情報を送信するにはレイヤーが多すぎます。



pix2pixHDは、入力画像のスケールを縮小する「エンコーダー」の助けを借りてこの問題をより効率的に解決し、出力画像を取得するためにスケールを拡大する「デコーダー」がそれに続きます。 すぐにわかるように、SPADEにはエンコーダーを必要としないよりエレガントなソリューションがあります。





pix2pixHDネットワーク図は「高」レベルです。 「残差」ブロックと「+操作」は、残差ニューラルネットワークの「スキップ接続」テクノロジーを指します 。 ネットワークにはスキップ可能なブロックがあり、エンコーダーとデコーダーで互いに関連しています。

バッチの正規化は問題です

ほぼすべての現代の畳み込みニューラルネットワークは、バッチ正規化またはそのアナログの1つを使用して、トレーニングプロセスを高速化し、安定させます。 各チャネルをアクティブにすると、チャネルパラメータのペアの前に平均が0に、標準偏差が1にシフトします。 $$$\ベータ$ そして $$$\ガンマ$ それらを再び非正規化します。



$$$y = \ frac {x-\ mathrm {E} [x]} {\ sqrt {\ mathrm {Var} [x] + \ epsilon}} * \ gamma + \ beta$



残念ながら、バッチの正規化はジェネレーターに害を及ぼし、ネットワークが特定の種類の画像処理を実装することを困難にします。 pix2pixHDは、画像のバッチを正規化する代わりに、各画像を個別に正規化する正規化標準を使用します。

Pix2pixHDトレーニング

pix2pixHDやSPADEなどの最新のGANは、生成コンテンションネットワークの元の設計で記述されたものとは少し異なって、出力画像のリアリズムを測定します。



高解像度画像を生成する問題を解決するために、pix2pixHDは同じ構造の3つのディスクリミネーターを使用します。各ディスクリミネーターは異なるスケール（通常サイズ、2倍、4倍）で出力画像を受け取ります。



Pix2pixHDが使用する $$$V_ \ text {LSGAN}$ 、およびジェネレータの結論をより現実的にするように設計された別の要素も含まれています（これが差別者を欺くのに役立つかどうかに関係なく）。 こちらの商品 $$$\ mathcal {L} _ \ text {FM}$ 「フィーチャマッチング」と呼ばれる-実際のデータとジェネレーターの出力との間の差別化のシミュレーションにおいて、ジェネレーターがレイヤーの分布を等しくすることを奨励し、 $$$L_1距離$ それらの間。



したがって、最適化は次のようになります。

$$ $$ display $$ \ begin {equation *} \ min_G \ bigg（\ lambda \ sum_ {k = 1,2,3} V_ \ text {LSGAN}（G、D_k）+ \ big（\ max_ {D_1、D_2 、D_3} \ sum_ {k = 1,2,3} \ mathcal {L} _ \ text {FM}（G、D_k）\ big）\ bigg）\ end {equation *}、$$ display $$

損失は​​3つの差別的要因と係数によって合計されます $$$\ラムダ= 10$ 、両方の要素の優先度を制御します。





pix2pixHDは、実際の寝室（各例の左側）で構成されるセグメンテーションマップを使用して、偽の寝室（右側）を作成します。



弁別器は、画像全体を分解するまで画像の縮尺を縮小しますが、サイズ70×70の「スポット」で停止します（適切な縮尺で）。 次に、画像全体のこれらの「スポット」の値をすべて要約します。



そして、このアプローチは機能します $$$\ mathcal {L} _ \ text {FM}$ 画像が高解像度でリアルに見えるように注意し、 $$$V_ \ text {LSGAN}$ 小さな部品をチェックするためにのみ必要です。 このアプローチには、ネットワークの高速化、使用されるパラメーターの数の削減、および任意のサイズの画像を生成するためにそれを使用する可能性という形で、追加の利点もあります。





pix2pixHDは、シンプルなアウトラインフェースから適切なしかめっ面を含む写実的な画像を生成します。 各例は、左側にCelebAデータセットからの実際の画像、このセレブの表情のスケッチのスケッチ、およびこのデータから作成された右側の画像を示しています。

pix2pixHDの何が問題になっていますか？

これらの結果は信じられないほどですが、さらに多くのことができます。 pix2pixHDは1つの重要な側面で多くを失います。



pix2pixHDが単一クラスの入力で、たとえばどこにでも草があるマップで何をするかを考えてください。 入力は空間的に均一であるため、最初の畳み込み層の出力も同じです。 次に、インスタンスの正規化は、画像内の各チャネルのすべての（同一の）値を「正規化」して返します $$$0$ それらすべての結論として。 βパラメーターはこの値をゼロからシフトできますが、事実は残ります。出力は、入力が「草」、「空」、「水」、または他の何かであることに依存しなくなります。









pix2pixHDでは、インスタンスの正規化はセグメンテーションマップからの情報を無視する傾向があります。 1つのクラスで構成される画像の場合、ネットワークはこのクラス自体に関係なく同じ画像を生成します。



そして、この問題の解決策は、SPADEの主要な設計機能です。

ソリューション：SPADE

最後に、セグメンテーションマップから画像を作成するという根本的に新しいレベルに到達しました。空間適応（de）正規化（SPADE）です。



SPADEの考え方は、ネットワーク内のセマンティック情報の損失を防ぎ、セグメンテーションマップが各個別のレベルでローカルに正規化パラメーターγおよびβを制御できるようにすることです。 各チャネルに1組のパラメーターのみを使用する代わりに、2つの畳み込み層を介したダウンサンプリングを使用してセグメンテーションマップを提供することにより、各空間ポイントに対してパラメーターが計算されます。





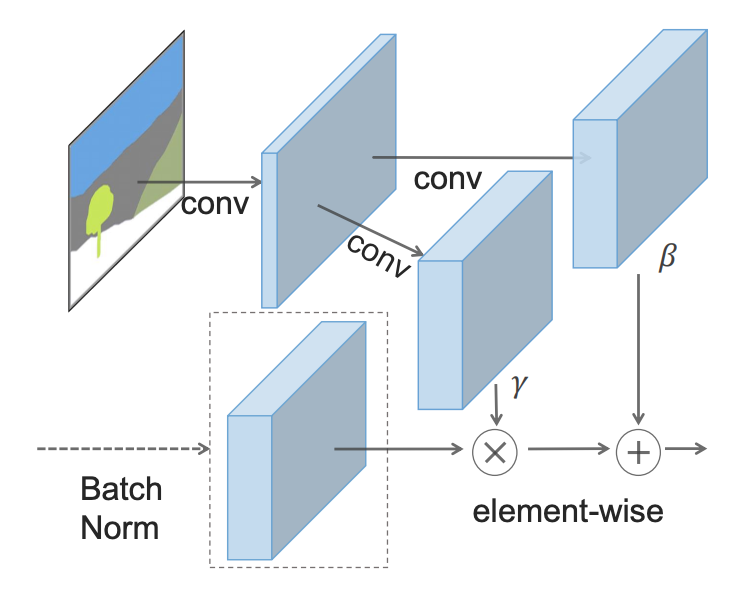
SPADEは、セグメンテーションマップを最初のレイヤーにロールする代わりに、ダウンサンプリングバージョンを使用して、各レイヤーの正規化された出力を変調します。



SPADEジェネレーターは、この設計全体を、アップサンプリングレイヤー（転置畳み込み）の間に配置される小さな「残留ブロック」に結合します。





pix2pixHDジェネレーターと比較したSPADEジェネレーターの高レベル回路



セグメンテーションマップはネットワークの「内側から」提供されるので、最初のレイヤーの入力として使用する必要はありません。 代わりに、ランダムなベクトルが入力として使用された元のGANスキームに戻ることができます。 これにより、1つのセグメンテーションマップからさまざまな画像を生成することができます（「マルチモーダル合成」）。 また、pix2pixHDの「エンコーダー」全体が不要になるため、大幅に簡素化されます。



SPADEはpix2pixHDと同じ損失関数を使用しますが、1つの変更があります。値を二乗する代わりに $$$V_ \ text {LSGAN}$ ヒンジ損失を使用します 。



これらの変更により、素晴らしい結果が得られます。





ここで、SPADEの結果をpix2pixHDの結果と比較します

直観

SPADEがこのような結果をどのように表示できるかを考えてみましょう。 以下の例では、ツリーがあります。 GauGANは1つの「ツリーのような」クラスを使用して、木の幹と葉の両方を表します。 しかし、どういうわけかSPADEは、「ツリー」の下部の狭い部分が幹であり、茶色でなければならず、一方、上部の大きなドロップは葉でなければならないことを発見します。



SPADEが各レイヤーを変調するために使用するダウンサンプリングセグメンテーションは、同様の「直感的な」認識を提供します。







木の幹は、「葉」を指す冠の部分で続いていることに気付くかもしれません。 それでは、SPADEは、トランクの一部をそこに配置する場所と、葉がどこにあるかをどのように理解しますか？ 確かに、5x5マップから判断すると、そこには単に「ツリー」が存在するはずです。



答えは、表示されたプロットは、5x5ブロックにツリー全体が含まれる低解像度レイヤーから情報を受け取ることができるということです。 その後の各畳み込み層も、画像内の情報の動きを提供し、より完全な画像を提供します。



SPADEを使用すると、セグメンテーションマップで各レイヤーを直接変調できますが、これにより、たとえばpix2pixHDのように、レイヤー間で情報が一貫して分配されるプロセスが妨げられることはありません。 これにより、セマンティック情報が失われるのを防ぎます。セマンティック情報は、前のレイヤーが原因で後続の各レイヤーで更新されるためです。

伝送スタイル

SPADEには、別の魔法の解決策があります-特定のスタイル（たとえば、照明、気象条件、季節）で画像を生成する機能です。





SPADEは、特定のスタイルを模倣して、1つのセグメンテーションカードに基づいていくつかの異なる画像を生成できます。



これは次のように機能します。エンコーダーを介して画像を渡し、生成ベクトルを設定するようにトレーニングします $$$Z$ 、同様の画像が生成されます。 エンコーダーがトレーニングされた後、対応するセグメンテーションカードを任意のカードに置き換えます。SPADEジェネレーターは、以前に受け取ったトレーニングに基づいて、提供された画像のスタイルで新しいカードに対応する画像を作成します。



ジェネレーターは通常、多次元正規分布に基づいてサンプルを受け取ることを想定しているため、現実的な画像を取得するには、同様の分布を持つ値を出力するようにエンコーダーをトレーニングする必要があります。 実際、これは変分オートエンコーダーのアイデアです。JoelZeldesが説明しています 。



これが、SPADE / GaiGANの機能です。 この記事が、新しいNVIDIAシステムがどのように機能するかについての好奇心を満たしてくれることを願っています。 Twitter @AdamDanielKinまたはadam@AdamDKing.comにメールで連絡してください。