プログラマーのためのGugology（これはタイプミスではありません）

物理学についてよりも数学について書くのは難しいので（それで面​​白いです）。 ただし、少なくともクレイジーなCプログラムの例をお読みください。









モンスターは完全に無害なものから成長することができます。 たとえば、部分文字列のゲームを考えてみましょう。 文字aとbの文字列を書き、メイン文字列の長さが十分になるまで、文字1から文字2、2から4、3から6、nから2nの部分文字列を選択します。 私たちのタスクは、これらの部分文字列で、短い文字列が長い文字列に入らないようにすることです。 SQLパーサーも作成しました。

declare @s varchar(max) = 'abbbaaaaaaab' declare @n int=1 declare @sub table (n int, sub varchar(max)) while @n*2<=len(@s) begin insert into @sub select @n,substring(@s,@n,@n+1) set @n=@n+1 end select *,(select max(sub) from @sub I where In>On and charindex(O.sub,I.sub)>0) as FoundMatch from @sub O order by 1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

出力例を次に示します。







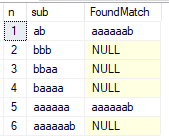
ご覧のとおり、サブストリング1と5はテストに合格しませんでした。 最後の文字を削除すると、結果の11文字の「abbbaaaaaaaa」の文字列がテストに合格します。 これは、この条件を満たす2文字のアルファベットで可能な限り長い文字列でもあることがわかります。



1文字のアルファベットの場合、最大文字列長は3であり、純粋に技術的な理由によります。 任意の数の文字のアルファベットの最大長は有限であることがわかります。 だから私たちは：

$$

$$f（1）= 3$$

$$

$$f（2）= 11$$

$$

$$f（3）= ???$$

3文字のアルファベットで文字列を作成できる長さについて直感をテストします。 100？ 1000？ 実際、Googolよりもはるかに多く、GoogolPlekhよりもはるかに多くです。

$$

$$f（3）> 2 \上矢印^ {7198} 158836$$

そして、シューターの強さを示すために時間を費やさなければなりません。

矢印（ハイパーオペレーション）

多くの加算演算を書かないように、乗算を使用します。

$$

$$2 * 5 = 2 + 2 + 2 + 2 + 2$$

べき乗を使用して、多くの乗算を記述しません。

$$

$$2 ^ 3 = 2 * 2 * 2$$

加算をレベル0の演算、1としての乗算、2としてのべき乗を考慮すると、たとえば、演算「矢印」を導入できます。

$$

$$3 \上矢印3 = 3 ^ {（3 ^ 3）} = 3 ^ {27} = 7'625'597'484'987$$

ここでは括弧がすでに重要であることに注意してください。 次のレベルは、2つの矢印操作です。

$$

$$3 \上矢印\上矢印3 = 3 \上矢印（3 \上矢印3）= 3 \上矢印7625597484987 = 3 ^ {3 ^ {... ^ 3}}$$

トリプルの最後のピラミッドの高さは70億で、この数はすでにかなり大きく、googolやgoogolpleksよりもはるかに大きくなっています。 この巨大な数字を暗闇として示し（古いロシア語ではそのような数字でした）、さらに一歩踏み出そうとします。

$$

$$3 \上矢印^ 3 3 = 3 \上矢印\上矢印\上矢印3 = 3 \上矢印\上矢印（3 \上矢印\上矢印3）= 3 \上矢印\上矢印{暗闇} = 3 \上矢印3 \上矢印3 ... \上矢印3$$

（そして何回も）...この数字がどれほど大きいかを想像することさえできます。 多くの矢印がある場合、上部にリピーターを書くことに注意してください。 だから、あなたはどれくらい素晴らしい

$$

$$f（3）> 2 \上矢印^ {7198} 158836$$

その他

矢印を使用すると、いわば、小さい数字だけが作成されます。 関数の成長率は、特定のスケールで測定されます-急成長する関数と比較することによって。 この階層の最初の関数は加算に対応し、2番目は乗算に、3番目は矢印に、n番目からn-2の矢印（おおよそ、正確ではありません）に対応します。 しかし、あなたは定義することができます

$$

$$f_w（n）= f_n（n）$$

このようなn = 3の関数は、1つの矢印に匹敵し、n = 4には2つの矢印があり、パラメーターnが大きくなると、静的な数の矢印で関数の成長を上回ります。



さらに進むことができます： $$$f_w、f_ {w + 1}、f_ {w + n}、f_ {w2}、f_ {w ^ 2}、f_ {w ^ w}、f_ {w ^ {w ^ {w}}}、f_ \イプシロン$ これらの関数は、序数で、またはロシア文学では序数で索引付けされます。 最初の序数の構造を示す図は記事の前にありますが、それらはさらに拡張され、さらに始まります

少し神秘主義

オメガの無限のピラミッドは序数を与えます $$$\ epsilon_0$ 。 この順序によって成長が測定される関数について読んでください。 関数が非常に速く成長するため、形式的な算術演算では、そのような関数がまったく定義されていないことを原則的に証明することはできません。



もちろん、ゲーデルの定理については、証明できないステートメントがあることを知っています。 しかし、原則として、そのような声明の唯一の例は、ゲーデルの構造そのものです（「私は証明できません」）。 グッドスタインの定理はそのような陳述の良い例です。



さらに、序数は何らかの方法で理論の力を測定することがわかります。 形式的算術の「強さ」は $$$\ epsilon_0$ 、 単純化されたクリプケ-プラテカ集合理論は、 フェファーマン- シューテ序数などの強さを持っています。

ブリキ-数学止血帯-C言語コンテスト

多数のコンペが開催されました。 いいえ、チューリングマシンのプログラミングはいまだに残酷すぎるため、sizeof（int）= infinityの抽象的な無限マシンにCを使用しました。 malloc（）を使用することもできます。また、スタックなどのメモリ量は無制限です。 プログラムの長さのみが制限されていました-プログラムは512バイト（スペースを除く）に収まる必要がありましたが、プリプロセッサ（#define）の使用は許可されていました。



結果は数学のウェブサイトに掲載されています 。 同時に、本物の数学者のサイトのデザインをチェックしてください。 結果はこちらです。 これがプログラムのテキストで、2位になりました。

$$

$$f_ {w ^ w}（10 ^ {500}）$$

 typedef int J; JP(J x,J y) { return x+y ? x%2 + y%2*2 + P(x/2,y/2)*4 : 0 ;} JH(J z) { return z ? z%2 + 2*H(z/4) : 0 ;} JI(J f,J e,J r){ return f ? P(P(f,e),r) : r ;} JM(J x,J e) { return x ? I(x%2, M(e,0), M(x/2, e+1)) : 0 ;} JD(J,J); JE(J f,J e,J r,J b) { return e ? E(1, D(e,b), I(b-1, D(e,b), I(f-1,e,r)), b) : I(f-1,e,r) ; } JD(J x,J b) { return x ? E( H(H(x)), H(H(x)/2), H(x/2), b) : 0 ;} JF(J x,J b) { return x ? F(D(x,b+1),b+1) : b ;} JG(J x) { return F(M(x,9), 9) ;} J f(J n,J x) { return n ? f(n-1, G(x ? f(n,x-1) : n)) : G(x) ;} J g(J x) { return f(x,x) ;} J h(J n,J x) { return n ? h(n-1, g(x ? h(n,x-1) : n)) : g(x) ;} J main(void) { return h(g(9),9) ;}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

受賞者のプログラムのテキストはもっと長いので、どこから始まるのかを見せたかっただけです。

 #define R { return #define PP ( #define LL ( #define TS (v, y, c, #define C ), #define X x) #define F );}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

しかし、コンテストの主催者でさえ、その数字がどれだけ大きいかを評価するのは難しいと感じました（ 非常に大きく書かれています）

忙しいビーバー

さて、小さな数字を扱うのに十分な、大きな数字をやってみましょう。 最大数を生成するプログラムを作成するために、ユニバーサルコンテストが開催されたと想像してください。 プログラムの数は512文字以下なので、もちろん絶対的な勝者が常にいます。 BB（512） -busy beaver functionとして指定しましょう。



BB（1024）>> BB（512）であることは明らかです。 しかし、BB機能自体はどのくらいの速さで成長しますか？ 私たちが出会ったすべてのものよりも速く成長していることがわかりました。 BB関数自体はアルゴリズム的に解決不可能であり、コンピューターで計算することはできません。 しかし、受け入れ可能なプログラムの長さが長くなれば、より多くの新しいアイデアを実装できます。 そのため、BBはアルゴリズムで決定可能な関数よりも速く成長します。

大きな足

さて、小さな数字を扱うのに十分な、大きな数字をやってみましょう。 あ、もう言った？ BB（BB（n））を実行するといいでしょう。 しかし、BBは計算できないため、これには技術的な困難があります（そのような関数は、オラクルとOracle DBMSを混同しないようにオラクルを持つチューリングマシンで計算可能です）。



ただし、 プログラムの代わりに、長さnの量指定子を含む数式を検討する方が簡単です。 数量詞の式は、何かが計算可能かどうかは関係ありません。 したがって、少なくとも関数BB（1,000,000,000）を取得し、BB（BB（BB（BB（1,000,000））））回適用できます。 そして、これは最初に思い浮かんだことです。



最大でn文字の数式で表すことができる最大数は、FOOT（n）で表されます。

$$

$$BIG FOOT = FOOT ^ {10}（10 ^ {100}）$$

PS

次の記事では、何に焦点を当てるべきかを理解したいので、調査に参加してください