Clever Geek Handbook

SIMDの種類

meshoptimizerの開発中に、「このアルゴリズムはSIMDを使用できますか？」という疑問がしばしば発生します。



ライブラリはパフォーマンスを重視していますが、SIMDが常に速度を大幅に向上させるとは限りません。 残念ながら、SIMDはコードの移植性と保守性を低下させる可能性があります。 したがって、それぞれのケースで、妥協点を探す必要があります。 パフォーマンスが最重要である場合、SSEおよびNEON命令セットの個別のSIMD実装を開発および維持する必要があります。 それ以外の場合は、SIMDを使用することの効果を理解する必要があります。 本日は、SSEn / AVXn命令セットを使用して、最近ライブラリに追加された新しいアルゴリズムであるずさんなメッシュシンプリファイアーの高速化を試みます。











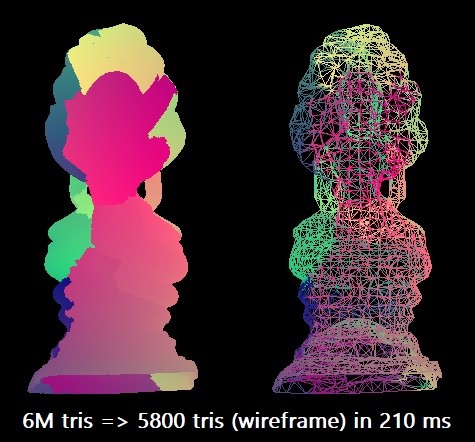
ベンチマークでは、タイ仏モデルを600万個の三角形からこの数の0.1％に簡素化します。 ターゲットx64アーキテクチャ用にMicrosoft Visual Studio 2019コンパイラを使用します。 スカラーアルゴリズムは、単一のIntel Core i7-8700Kスレッド（約4.4 GHz）で約210ミリ秒でこのような合理化を実行できます。 これは、1秒あたり約2850万の三角形に相当します。 実際にはこれで十分かもしれませんが、機器の最大能力を探求したいと思いました。



場合によっては、グリッドを断片に分割することで手順を並列化できますが、このためには境界を維持するために接続性の追加分析を行う必要があるため、ここでは純粋なSIMD最適化に制限します。



七次元



最適化の可能性を理解するために、インテルVTuneを使用してプロファイリングを実行します。 手順を100回実行して、十分なデータがあることを確認します。







ここでは、各機能の実行時間を修正し、ボトルネックを見つけるために、マイクロアーキテクチャモードをオンにしました。 合理化は一連の関数を使用して実行され、各関数には一定のサイクル数が必要であることがわかります。 関数のリストは時間でソートされます。 ここでは、アルゴリズムを理解しやすくするために、実行順に並んでいます。





computeVertexIds



およびcountTriangles



は数回実行されます：アルゴリズムは、頂点をマージするためのメッシュサイズを決定し、加速バイナリ検索を実行してターゲットの三角形の数（この場合は6000）を達成し、各メッシュサイズが各反復で生成する三角形の数を計算します。 他の機能は一度起動されます。 このファイルでは、5回の検索パスでターゲットメッシュサイズが40 3になります。



VTuneは、リソースを最も多く消費する関数が2次関数を計算する関数であることを義務的に報告します。これには、21秒間の合計実行時間のほぼ半分がかかります。 これは、SIMDを最適化するための最初の目標です。



SIMDピースバイピース



fillCellQuadrics



のソースコードを見て、計算対象を正確に理解してみましょう。 



 static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); float weight = single_cell ? 3.f : 1.f; Quadric Q; quadricFromTriangle(Q, vertex_positions[i0], vertex_positions[i1], vertex_positions[i2], weight); if (single_cell) { quadricAdd(cell_quadrics[c0], Q); } else { quadricAdd(cell_quadrics[c0], Q); quadricAdd(cell_quadrics[c1], Q); quadricAdd(cell_quadrics[c2], Q); } } }


この関数は、すべての三角形を反復処理し、各三角形の2次関数を計算して、各セルの2次関数に追加します。 Quadric-10の浮動小数点数として表される4×4対称行列： 



 struct Quadric { float a00; float a10, a11; float a20, a21, a22; float b0, b1, b2, c; };


二次関数の計算には、三角形の平面方程式を解き、二次行列を作成し、三角形の面積を使用して重み付けする必要があります。 



 static void quadricFromPlane(Quadric& Q, float a, float b, float c, float d) { Q.a00 = a * a; Q.a10 = b * a; Q.a11 = b * b; Q.a20 = c * a; Q.a21 = c * b; Q.a22 = c * c; Q.b0 = d * a; Q.b1 = d * b; Q.b2 = d * c; Qc = d * d; } static void quadricFromTriangle(Quadric& Q, const Vector3& p0, const Vector3& p1, const Vector3& p2, float weight) { Vector3 p10 = {p1.x - p0.x, p1.y - p0.y, p1.z - p0.z}; Vector3 p20 = {p2.x - p0.x, p2.y - p0.y, p2.z - p0.z}; Vector3 normal = { p10.y * p20.z - p10.z * p20.y, p10.z * p20.x - p10.x * p20.z, p10.x * p20.y - p10.y * p20.x }; float area = normalize(normal); float distance = normal.x*p0.x + normal.y*p0.y + normal.z*p0.z; quadricFromPlane(Q, normal.x, normal.y, normal.z, -distance); quadricMul(Q, area * weight); }


浮動小数点演算が多数あるように見えるため、SIMDを使用して並列化できます。 最初に、各ベクトルを4幅のSIMDベクトルとして表し、また、 Quadric



構造を10ではなく12の浮動小数点数に変更して、3つのSIMDレジスタに正確に適合し（サイズを大きくしてもパフォーマンスに影響しない）、フィールドの順序を変更して計算を行いますquadricFromPlane



はより均一になりました。 



 struct Quadric { float a00, a11, a22; float pad0; float a10, a21, a20; float pad1; float b0, b1, b2, c; };


ここで、一部の計算、特にスカラー積は、SSEの以前のバージョンとあまり一貫性がありません。 幸いなことに、スカラー積の命令がSSE4.1に登場しました。これは非常に便利です。 



 static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { const int yzx = _MM_SHUFFLE(3, 0, 2, 1); const int zxy = _MM_SHUFFLE(3, 1, 0, 2); const int dp_xyz = 0x7f; for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); __m128 p0 = _mm_loadu_ps(&vertex_positions[i0].x); __m128 p1 = _mm_loadu_ps(&vertex_positions[i1].x); __m128 p2 = _mm_loadu_ps(&vertex_positions[i2].x); __m128 p10 = _mm_sub_ps(p1, p0); __m128 p20 = _mm_sub_ps(p2, p0); __m128 normal = _mm_sub_ps( _mm_mul_ps( _mm_shuffle_ps(p10, p10, yzx), _mm_shuffle_ps(p20, p20, zxy)), _mm_mul_ps( _mm_shuffle_ps(p10, p10, zxy), _mm_shuffle_ps(p20, p20, yzx))); __m128 areasq = _mm_dp_ps(normal, normal, dp_xyz); // SSE4.1 __m128 area = _mm_sqrt_ps(areasq); // masks the result of the division when area==0 // scalar version does this in normalize() normal = _mm_and_ps( _mm_div_ps(normal, area), _mm_cmpneq_ps(area, _mm_setzero_ps())); __m128 distance = _mm_dp_ps(normal, p0, dp_xyz); // SSE4.1 __m128 negdistance = _mm_sub_ps(_mm_setzero_ps(), distance); __m128 normalnegdist = _mm_blend_ps(normal, negdistance, 8); __m128 Qx = _mm_mul_ps(normal, normal); __m128 Qy = _mm_mul_ps( _mm_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)), _mm_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0))); __m128 Qz = _mm_mul_ps(negdistance, normalnegdist); if (single_cell) { area = _mm_mul_ps(area, _mm_set1_ps(3.f)); Qx = _mm_mul_ps(Qx, area); Qy = _mm_mul_ps(Qy, area); Qz = _mm_mul_ps(Qz, area); Quadric& q0 = cell_quadrics[c0]; __m128 q0x = _mm_loadu_ps(&q0.a00); __m128 q0y = _mm_loadu_ps(&q0.a10); __m128 q0z = _mm_loadu_ps(&q0.b0); _mm_storeu_ps(&q0.a00, _mm_add_ps(q0x, Qx)); _mm_storeu_ps(&q0.a10, _mm_add_ps(q0y, Qy)); _mm_storeu_ps(&q0.b0, _mm_add_ps(q0z, Qz)); } else { // omitted for brevity, repeats the if() body // three times for c0/c1/c2 } } }


このコードには特に興味深いものはありません。 アラインされていないロード/ストア命令を豊富に使用しています。 Vector3の入力はアライメントできますが、アライメントされていない読み取りに対して目立ったペナルティはないようです。 関数の前半ではベクトルが使用されていないことに注意してください-ベクトルは3つのコンポーネントを持ち、場合によっては1つだけです（areasq / area / distanceの計算を参照）。一方、プロセッサは4つの操作を並行して実行します。 いずれにせよ、並列化がどのように役立つかを見てみましょう。







fillCellQuadrics



の100回の開始が9.8秒ではなく5.3秒で実行されるようになり、各操作で約45ミリ秒節約されます-悪くはありませんが、それほど印象的ではありません。 多くの命令では、4つのコンポーネントの代わりに3つのコンポーネントを使用し、正確な乗算を使用しているため、かなりの遅延が発生します。 以前にSIMDの指示を書いたことがあれば、スカラー積を正しく行う方法を知っています。



これを行うには、一度に4つのベクトルを実行する必要があります。 1つのSIMDレジスタに1つのフルベクトルを格納する代わりに、3つのレジスタを使用します。1つはx



4つのコンポーネントを格納し、もう1つは



を格納し、3番目のz



格納します。 ここでは、一度に4つのベクトルが必要です。つまり、4つの三角形を同時に処理します。



動的インデックスを使用した配列が多数あります。 通常、 x



/ y



/ z



コンポーネントの準備された配列にデータを転送するのに役立ちます（または、むしろ、入力の8つの頂点のそれぞれに対して、たとえば、 float x[8], y[8], z[8]



などの小さなSIMDレジスタが通常使用されますデータ：これはAoSoA（配列構造の配列）と呼ばれ、キャッシュの局所性とSIMDレジスターへのロードの容易さのバランスが取れています）が、ここでは動的なインデックス付けはあまりうまく動作しないため、通常のように4つの三角形のデータをロードし、便利な方法でベクトルを転置しますマクロ_MM_TRANSPOSE







理論的には、独自のSIMDレジスタで4つの有限2次の各コンポーネントを計算する必要があります（たとえば、 a00



有限2次の4つのコンポーネントを持つ__m128 Q_a00があります）。 この場合、2次関数の演算は4ワイドのSIMD命令に非常によく適合し、変換により実際にコードの速度が低下します。したがって、初期ベクトルのみを転置し、次に平面方程式を転置して、2次関数の計算に使用したのと同じコードを実行しますが、それを繰り返します4回。 コードは次のようになり、平面方程式を計算します（残りの部分は簡潔にするために省略されています）。 



 unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; unsigned int i20 = indices[(i + 2) * 3 + 0]; unsigned int i21 = indices[(i + 2) * 3 + 1]; unsigned int i22 = indices[(i + 2) * 3 + 2]; unsigned int i30 = indices[(i + 3) * 3 + 0]; unsigned int i31 = indices[(i + 3) * 3 + 1]; unsigned int i32 = indices[(i + 3) * 3 + 2]; // load first vertex of each triangle and transpose into vectors with components (pw0 isn't used later) __m128 px0 = _mm_loadu_ps(&vertex_positions[i00].x); __m128 py0 = _mm_loadu_ps(&vertex_positions[i10].x); __m128 pz0 = _mm_loadu_ps(&vertex_positions[i20].x); __m128 pw0 = _mm_loadu_ps(&vertex_positions[i30].x); _MM_TRANSPOSE4_PS(px0, py0, pz0, pw0); // load second vertex of each triangle and transpose into vectors with components __m128 px1 = _mm_loadu_ps(&vertex_positions[i01].x); __m128 py1 = _mm_loadu_ps(&vertex_positions[i11].x); __m128 pz1 = _mm_loadu_ps(&vertex_positions[i21].x); __m128 pw1 = _mm_loadu_ps(&vertex_positions[i31].x); _MM_TRANSPOSE4_PS(px1, py1, pz1, pw1); // load third vertex of each triangle and transpose into vectors with components __m128 px2 = _mm_loadu_ps(&vertex_positions[i02].x); __m128 py2 = _mm_loadu_ps(&vertex_positions[i12].x); __m128 pz2 = _mm_loadu_ps(&vertex_positions[i22].x); __m128 pw2 = _mm_loadu_ps(&vertex_positions[i32].x); _MM_TRANSPOSE4_PS(px2, py2, pz2, pw2); // p1 - p0 __m128 px10 = _mm_sub_ps(px1, px0); __m128 py10 = _mm_sub_ps(py1, py0); __m128 pz10 = _mm_sub_ps(pz1, pz0); // p2 - p0 __m128 px20 = _mm_sub_ps(px2, px0); __m128 py20 = _mm_sub_ps(py2, py0); __m128 pz20 = _mm_sub_ps(pz2, pz0); // cross(p10, p20) __m128 normalx = _mm_sub_ps( _mm_mul_ps(py10, pz20), _mm_mul_ps(pz10, py20)); __m128 normaly = _mm_sub_ps( _mm_mul_ps(pz10, px20), _mm_mul_ps(px10, pz20)); __m128 normalz = _mm_sub_ps( _mm_mul_ps(px10, py20), _mm_mul_ps(py10, px20)); // normalize; note that areasq/area now contain 4 values, not just one __m128 areasq = _mm_add_ps( _mm_mul_ps(normalx, normalx), _mm_add_ps( _mm_mul_ps(normaly, normaly), _mm_mul_ps(normalz, normalz))); __m128 area = _mm_sqrt_ps(areasq); __m128 areanz = _mm_cmpneq_ps(area, _mm_setzero_ps()); normalx = _mm_and_ps(_mm_div_ps(normalx, area), areanz); normaly = _mm_and_ps(_mm_div_ps(normaly, area), areanz); normalz = _mm_and_ps(_mm_div_ps(normalz, area), areanz); __m128 distance = _mm_add_ps( _mm_mul_ps(normalx, px0), _mm_add_ps( _mm_mul_ps(normaly, py0), _mm_mul_ps(normalz, pz0))); __m128 negdistance = _mm_sub_ps(_mm_setzero_ps(), distance); // this computes the plane equations (a, b, c, d) for each of the 4 triangles __m128 plane0 = normalx; __m128 plane1 = normaly; __m128 plane2 = normalz; __m128 plane3 = negdistance; _MM_TRANSPOSE4_PS(plane0, plane1, plane2, plane3);


コードはもう少し長くなりました。各反復で4つの三角形を処理するようになり、このためのSSE4.1命令は不要になりました。 理論的には、SIMDユニットをより効率的に使用する必要があります。 それがどのように役立つか見てみましょう。







大丈夫、大丈夫です。 fillCellQuadrics



関数はSIMDなしで元の関数のほぼ2倍の速度で実行されますが、コードはわずかに加速しますが、これが複雑さの大幅な増加を正当化するかどうかは不明です。 理論的には、AVX2を使用して反復ごとに8つの三角形を処理できますが、ここではループを手動でさらにスピンする必要があります（理想的には、このコードはすべてISPCを使用して生成されますが、良いコードを生成するための私の素朴な試みは成功しませんでした：シーケンスのロード/保存の代わりに彼は持続的にギャザー/スキャッターを発行したため、実行速度が大幅に低下しました。 他のことを試してみましょう。



AVX2 = SSE2 + SSE2



AVX2は、少し独特な一連の命令です。 8幅の浮動小数点レジスターがあり、1つの命令で8つの操作を実行できます。 しかし、実際には、そのような命令は、レジスターの半分で実行される2つのSSE2命令と違いはありません（私の知る限り、AVX2を搭載した最初のプロセッサーは、2つ以上のマイクロオペレーションで各命令をデコードすることをサポートしているため、パフォーマンスの向上は命令の抽出フェーズによって制限されていました）。 たとえば、 _mm_dp_ps



は2つのSSE2レジスタ間でスカラー積を実行し、 _mm256_dp_ps



は2つのAVX2レジスタの2つの半分間で2つのスカラー積を生成するため、半分ごとに4幅に制限されます。



このため、AVX2コードは普遍的な「8ワイドSIMD」とは異なる場合がありますが、ここでは有利に機能します。4ワイドベクトルを転置してベクトル化を改善する代わりに、SSE2の代わりにAVX2命令を使用して最初のバージョンのSIMDに戻り、ループを2倍にします/ SSE4。 4幅のベクトルをロードして保存する必要がありますが、一般的には、いくつかの設定で_mm256



_mm_



を_mm256



に、 _mm_



を_mm256



に変更するだけです。 



 unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; __m256 p0 = _mm256_loadu2_m128( &vertex_positions[i10].x, &vertex_positions[i00].x); __m256 p1 = _mm256_loadu2_m128( &vertex_positions[i11].x, &vertex_positions[i01].x); __m256 p2 = _mm256_loadu2_m128( &vertex_positions[i12].x, &vertex_positions[i02].x); __m256 p10 = _mm256_sub_ps(p1, p0); __m256 p20 = _mm256_sub_ps(p2, p0); __m256 normal = _mm256_sub_ps( _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, yzx), _mm256_shuffle_ps(p20, p20, zxy)), _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, zxy), _mm256_shuffle_ps(p20, p20, yzx))); __m256 areasq = _mm256_dp_ps(normal, normal, dp_xyz); __m256 area = _mm256_sqrt_ps(areasq); __m256 areanz = _mm256_cmp_ps(area, _mm256_setzero_ps(), _CMP_NEQ_OQ); normal = _mm256_and_ps(_mm256_div_ps(normal, area), areanz); __m256 distance = _mm256_dp_ps(normal, p0, dp_xyz); __m256 negdistance = _mm256_sub_ps(_mm256_setzero_ps(), distance); __m256 normalnegdist = _mm256_blend_ps(normal, negdistance, 0x88); __m256 Qx = _mm256_mul_ps(normal, normal); __m256 Qy = _mm256_mul_ps( _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)), _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0))); __m256 Qz = _mm256_mul_ps(negdistance, normalnegdist);


ここで、受信したQx



/ Qz



/ Qz



128ビットの半分ごとに、2次関数を追加するために使用したのと同じコードを実行できます。 代わりに、三角形の1つのセルに3つの頂点がある場合（ single_cell == true



）、別の三角形に別のセルの3つの頂点がある可能性が非常に高いと想定し、AVX2を使用して2次の最終集約も実行します： 



 unsigned int c00 = vertex_cells[i00]; unsigned int c01 = vertex_cells[i01]; unsigned int c02 = vertex_cells[i02]; unsigned int c10 = vertex_cells[i10]; unsigned int c11 = vertex_cells[i11]; unsigned int c12 = vertex_cells[i12]; bool single_cell = (c00 == c01) & (c00 == c02) & (c10 == c11) & (c10 == c12); if (single_cell) { area = _mm256_mul_ps(area, _mm256_set1_ps(3.f)); Qx = _mm256_mul_ps(Qx, area); Qy = _mm256_mul_ps(Qy, area); Qz = _mm256_mul_ps(Qz, area); Quadric& q00 = cell_quadrics[c00]; Quadric& q10 = cell_quadrics[c10]; __m256 q0x = _mm256_loadu2_m128(&q10.a00, &q00.a00); __m256 q0y = _mm256_loadu2_m128(&q10.a10, &q00.a10); __m256 q0z = _mm256_loadu2_m128(&q10.b0, &q00.b0); _mm256_storeu2_m128(&q10.a00, &q00.a00, _mm256_add_ps(q0x, Qx)); _mm256_storeu2_m128(&q10.a10, &q00.a10, _mm256_add_ps(q0y, Qy)); _mm256_storeu2_m128(&q10.b0, &q00.b0, _mm256_add_ps(q0z, Qz)); } else { // omitted for brevity }


結果のコードは、失敗したSSE2アプローチよりも単純、簡潔、高速です。







もちろん、8倍の加速は達成しませんでしたが、2.45倍しか達成しませんでした。 動的なインデックス付けのために不便なメモリレイアウトで作業することを余儀なくされるため、ロードおよびストレージ操作は依然として4ワイドであり、計算はSIMDに最適ではありません。 しかし、今ではfillCellQuadrics



プロファイルのパイプラインのボトルネックでfillCellQuadrics



なくなり、他の機能に集中できます。



集まって、子供たち



テスト実行で4.8秒（各実行で48ミリ秒）を節約し、現在の主な侵入者はcountTriangles



です。 単純な関数のように見えますが、1回ではなく5回実行されます。 



 static size_t countTriangles(const unsigned int* vertex_ids, const unsigned int* indices, size_t index_count) { size_t result = 0; for (size_t i = 0; i < index_count; i += 3) { unsigned int id0 = vertex_ids[indices[i + 0]]; unsigned int id1 = vertex_ids[indices[i + 1]]; unsigned int id2 = vertex_ids[indices[i + 2]]; result += (id0 != id1) & (id0 != id2) & (id1 != id2); } return result; }


この関数は、すべてのソース三角形を反復処理し、頂点の識別子を比較して非縮退三角形の数を計算します。 ギャザー命令を使用しない限り、SIMDを使用して並列化する方法はすぐにはわかりません。



AVX2命令セットは、x64 SIMDにGather / Scatter命令ファミリを追加しました。 それぞれが4つまたは8つの値を持つベクトルレジスタを受け取り、同時に4つまたは8つのロードまたは保存操作を実行します。 ここでGatherを使用すると、3つのインデックスをダウンロードし、Gatherを一度に（または4または8のグループで）実行して、結果を比較できます。 Intelプロセッサでの収集は、これまでかなり低速でしたが、試してみましょう。 簡単にするために、8つの三角形のデータをアップロードし、以前の試みと同じ方法でベクトルを転置し、各ベクトルの対応する要素を比較します。 



 for (size_t i = 0; i < (triangle_count & ~7); i += 8) { __m256 tri0 = _mm256_loadu2_m128( (const float*)&indices[(i + 4) * 3 + 0], (const float*)&indices[(i + 0) * 3 + 0]); __m256 tri1 = _mm256_loadu2_m128( (const float*)&indices[(i + 5) * 3 + 0], (const float*)&indices[(i + 1) * 3 + 0]); __m256 tri2 = _mm256_loadu2_m128( (const float*)&indices[(i + 6) * 3 + 0], (const float*)&indices[(i + 2) * 3 + 0]); __m256 tri3 = _mm256_loadu2_m128( (const float*)&indices[(i + 7) * 3 + 0], (const float*)&indices[(i + 3) * 3 + 0]); _MM_TRANSPOSE8_LANE4_PS(tri0, tri1, tri2, tri3); __m256i i0 = _mm256_castps_si256(tri0); __m256i i1 = _mm256_castps_si256(tri1); __m256i i2 = _mm256_castps_si256(tri2); __m256i id0 = _mm256_i32gather_epi32((int*)vertex_ids, i0, 4); __m256i id1 = _mm256_i32gather_epi32((int*)vertex_ids, i1, 4); __m256i id2 = _mm256_i32gather_epi32((int*)vertex_ids, i2, 4); __m256i deg = _mm256_or_si256( _mm256_cmpeq_epi32(id1, id2), _mm256_or_si256( _mm256_cmpeq_epi32(id0, id1), _mm256_cmpeq_epi32(id0, id2))); result += 8 - _mm_popcnt_u32(_mm256_movemask_epi8(deg)) / 4; }


AVX2の_MM_TRANSPOSE8_LANE4_PS



マクロは_MM_TRANSPOSE4_PS



に相当します。これは標準ヘッダーにはありませんが、簡単に表示されます。 4つのAVX2ベクトルを受け取り、2つの4×4行列を互いに独立して転置します。 



 #define _MM_TRANSPOSE8_LANE4_PS(row0, row1, row2, row3) \ do { \ __m256 __t0, __t1, __t2, __t3; \ __t0 = _mm256_unpacklo_ps(row0, row1); \ __t1 = _mm256_unpackhi_ps(row0, row1); \ __t2 = _mm256_unpacklo_ps(row2, row3); \ __t3 = _mm256_unpackhi_ps(row2, row3); \ row0 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(1, 0, 1, 0)); \ row1 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(3, 2, 3, 2)); \ row2 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(1, 0, 1, 0)); \ row3 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(3, 2, 3, 2)); \ } while (0)


SSE2 / AVX2命令セットにはいくつかの機能があるため、ベクトルを転置するときには浮動小数点レジスター演算を使用する必要があります。 データを少し不注意にロードしています。 しかし、基本的には重要ではありません。これは、パフォーマンスの収集によって制限されるためです。







countTriangles



は約27％高速になり、ひどいCPI（命令あたりのサイクル）に気づきました。約4倍少ない命令を送信しますが、収集には多くの時間がかかります。 全体の作業が高速化されるのは素晴らしいことですが、もちろん、パフォーマンスの向上はいくぶん落ち込みます。 プロファイル内のfillCellQuadrics



を追い越して、リストの一番上にある最後の関数に移動しましたが、まだ見ていません。



第6章、すべてが正常に機能し始める



最後の関数はcomputeVertexIds



です。 アルゴリズムでは6回実行されるため、最適化の優れた目標でもあります。 SIMDで明確な最適化のために作成されたと思われる関数が初めて見られます。 



 static void computeVertexIds(unsigned int* vertex_ids, const Vector3* vertex_positions, size_t vertex_count, int grid_size) { assert(grid_size >= 1 && grid_size <= 1024); float cell_scale = float(grid_size - 1); for (size_t i = 0; i < vertex_count; ++i) { const Vector3& v = vertex_positions[i]; int xi = int(vx * cell_scale + 0.5f); int yi = int(vy * cell_scale + 0.5f); int zi = int(vz * cell_scale + 0.5f); vertex_ids[i] = (xi << 20) | (yi << 10) | zi; } }


前の最適化の後、何をすべきかを知っています：サイクルを4回または8回展開します。1回の反復だけを高速化しようとしても意味がないため、ベクトル成分を転置し、並行して計算を開始します。 AVX2を使用してこれを行い、一度に8つの頂点を処理します。 



 __m256 scale = _mm256_set1_ps(cell_scale); __m256 half = _mm256_set1_ps(0.5f); for (size_t i = 0; i < (vertex_count & ~7); i += 8) { __m256 vx = _mm256_loadu2_m128( &vertex_positions[i + 4].x, &vertex_positions[i + 0].x); __m256 vy = _mm256_loadu2_m128( &vertex_positions[i + 5].x, &vertex_positions[i + 1].x); __m256 vz = _mm256_loadu2_m128( &vertex_positions[i + 6].x, &vertex_positions[i + 2].x); __m256 vw = _mm256_loadu2_m128( &vertex_positions[i + 7].x, &vertex_positions[i + 3].x); _MM_TRANSPOSE8_LANE4_PS(vx, vy, vz, vw); __m256i xi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vx, scale), half)); __m256i yi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vy, scale), half)); __m256i zi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vz, scale), half)); __m256i id = _mm256_or_si256( zi, _mm256_or_si256( _mm256_slli_epi32(xi, 20), _mm256_slli_epi32(yi, 10))); _mm256_storeu_si256((__m256i*)&vertex_ids[i], id); }


そして結果を見てください：2回







加速computeVertexIds



しました。すべての最適化を考慮して、プログラムの合計実行時間は約120ミリ秒に短縮されました。これは、1秒あたり5,000万の三角形の計算に相当します。



予想される生産性の向上を再び達成できなかったように思えるかもしれませcomputeVertexIds



ん。並列化後に2倍以上加速すべきではないでしょうか。この質問に答えるために、この関数が実行する作業の量を確認してみましょう。



computeVertexIds



1回のプログラム開始で6回実行されます。バイナリ検索中に5回、最後に1回実行されて、さらなる処理に使用される最終識別子が計算されます。この関数は300万個の頂点を処理するたびに、各頂点に対して12バイトを読み取り、4バイトを書き込みます。



合計100回を超えるイノベーターの実行で、この関数は18億の頂点を処理し、21 GBを読み取り、7 GBを書き戻します。 1.46秒で28 GBを処理するには、19 GB / sのバス帯域幅が必要です。を実行して、メモリ帯域幅を確認できmemcmp(block1, block2, 512 MB)



ます。結果は45ミリ秒、つまり、1つのコアで約22 GB /秒です（ただし、AIDA64ベンチマークは私のシステムで最大31 GB /秒の読み取り速度を示しますが、複数のコアを使用します）。実際、達成可能な最大メモリ制限に近づいており、パフォーマンスをさらに向上させるには、これらの頂点を12バイト未満に抑えるために、これらの頂点をより密にパッキングする必要があります。



おわりに



毎秒2800万トライアングルの速度で非常に大きなグリッドを簡素化する、かなり最適化されたアルゴリズムを採用し、SSEおよびAVX命令セットを使用して、ほぼ2倍、1秒あたり5,000万トライアングルまで高速化しました。この過程で、SIMDのさまざまな使用方法を学習する必要がありました。3ワイドベクトルを格納するレジスタ、SoA転置、2つの3ワイドベクトルを格納するAVX2命令、スカラー命令と比較してデータロードを高速化する命令を収集し、最後にストリーミング処理にAVX2を直接適用しました。



多くの場合、SIMDは最適化の最適な出発点ではありません。メッシュオプティマイザーは、プラットフォーム固有の命令を使用せずに、アルゴリズム最適化とマイクロ最適化の多くの反復を実行しました。しかし、ある時点で、これらの可能性は使い果たされ、パフォーマンスが重要な場合、SIMDは必要に応じて使用できる素晴らしいツールです。



これらの最適化がメインブランチに当てはまるmeshoptimizer



かどうかはわかりません。最終的に、これは、アルゴリズムを根本的に変更せずにコードがどれだけ加速するかを確認するための単なる実験です。この記事が有益であり、コードを最適化するためのアイデアを提供してくれることを願っています。この記事の最終情報源はこちらです。この作業は、meshoptimizer 99ab49のバージョンに基づいています、そしてタイ仏モデルがSketchfabで公開されています。


More articles:


All Articles