Clever Geek Handbook

並列C ++アルゴリズムの驚異的なパフォーマンス17。 神話か現実か？

こんばんは



コース「C ++ Developer」から、並列アルゴリズムに関する小規模で興味深い研究を提供します。



行こう



C ++ 17の並列アルゴリズムの出現により、「コンピューティング」コードを簡単に更新し、並列実行のメリットを享受できます。 この記事では、独立したコンピューティングの概念を自然に明らかにするSTLアルゴリズムを検討します。 10コアプロセッサで10倍の高速化を期待できますか？ それとももっと？ それ以下？ それについて話しましょう。



並列アルゴリズムの紹介







C ++ 17は、ほとんどのアルゴリズムに対して実行ポリシー設定を提供します。





簡単に：





簡単な例として、 std::sort



callを並列に呼び出します： 



 std::sort(std::execution::par, myVec.begin(), myVec.end()); // ^^^^^^^^^^^^^^^^^^^ //


アルゴリズムに並列実行パラメーターを追加するのがどれほど簡単かに注意してください！ しかし、パフォーマンスが大幅に改善されるのでしょうか？ 速度が上がりますか？ それとも減速がありますか？



並列std::transform







この記事では、他の並列メソッド（ std::transform_reduce



、 for_each



、 scan



、 sort



...とともに）の基礎となる可能性があるstd::transform



アルゴリズムに注意を払いたいと思います。



テストコードは、次のテンプレートに従って構築されます。 



 std::transform(execution_policy, // par, seq, par_unseq inVec.begin(), inVec.end(), outVec.begin(), ElementOperation);


ElementOperation



関数に同期メソッドがないと仮定します。この場合、コードには並列実行またはベクトル化の可能性があります。 各要素の計算は独立しており、順序は重要ではありません。そのため、実装は要素の独立した処理のために複数のスレッドを（スレッドプール内に）生成できます。



次のことを試してみたい：





ご覧のとおり、並列アルゴリズムを使用するのに「良い」要素の数だけでなく、プロセッサを占有するALU操作もテストします。

ソート、累積（std :: reduceの形式）などの他のアルゴリズムも並列実行を提供しますが、結果を計算するためにより多くの作業が必要です。 したがって、それらを別の記事の候補と見なします。



ベンチマークノート



私のテストでは、Visual Studio 2017、15.8を使用します。これは、現時点（2018年11月）で人気のあるコンパイラ/ STL実装の唯一の実装であるためです（途中GCC！）。 さらに、 execution::par_unseq



MSVCでは使用できないため、 execution::par



のみに焦点を合わせました（ execution::par



と同様に機能します）。



2つのコンピューターがあります。





コードはx64でコンパイルされ、Release more、自動ベクトル化はデフォルトで有効になっています。コマンドの拡張セット（SSE2）とOpenMP（2.0）も含まれています。



コードは私のgithubにあります： github / fenbf / ParSTLTests / TransformTests / TransformTests.cpp



OpenMP（2.0）の場合、ループに対してのみ並列処理を使用します。 



 #pragma omp parallel for for (int i = 0; ...)


コードを5回実行し、最小の結果を確認します。



警告 ：結果は大まかな観察結果のみを反映しているため、実稼働環境で使用する前にシステム/構成を確認してください。 要件と環境は私の要件と異なる場合があります。



この投稿で MSVCの実装について詳しく読むことができます。 そして、CppCon 2018 に関するビル・オニールの最新レポートです（ビルはMSVCでパラレルSTLを実装しました）。



さて、簡単な例から始めましょう！



簡単な変換



入力ベクトルに非常に簡単な操作を適用する場合を考えてください。 要素のコピーまたは乗算が可能です。



例： 



 std::transform(std::execution::par, vec.begin(), vec.end(), out.begin(), [](double v) { return v * 2.0; } );


コンピューターに6コアまたは4コアがあります。4..6倍の順次実行を期待できますか？ ここに私の結果があります（ミリ秒単位の時間）：



運営 ベクターサイズ i7 4720（4コア） i7 8700（6コア）
実行:: seq 10k 0.002763 0.001924
実行::パー 10k 0.009869 0.008983
のopenmp並列 10k 0.003158 0.002246
実行:: seq 10万 0.051318 0.028872
実行::パー 10万 0.043028 0.025664
のopenmp並列 10万 0.022501 0.009624
実行:: seq 1000k 1.69508 0.52419
実行::パー 1000k 1.65561 0.359619
のopenmp並列 1000k 1.50678 0.344863


より高速なマシンでは、パフォーマンスの向上に気付くには約100万の要素が必要であることがわかります。 一方、私のラップトップでは、すべての並列実装が遅くなりました。



したがって、要素の数が増えても、このような変換を使用すると、パフォーマンスが大幅に向上することに気付くことは困難です。



なぜそうですか？



操作は基本的なものであるため、プロセッサコアは数サイクルのみを使用してほぼ瞬時に呼び出すことができます。 ただし、プロセッサコアはメインメモリの待機により多くの時間を費やします。 したがって、この場合、ほとんどの場合、計算を行わずに待機します。



メモリ内の変数の読み取りと書き込みは、キャッシュされている場合は約2〜3サイクル、キャッシュされていない場合は数百サイクルかかります。

https://www.agner.org/optimize/optimizing_cpp.pdf



アルゴリズムがメモリに依存している場合、並列計算によるパフォーマンスの向上は期待できないことに大まかに注意できます。



その他の計算



メモリ帯域幅は非常に重要であり、物事の速度に影響を与える可能性があるため...各要素に影響する計算量を増やしましょう。



アイデアは、メモリを待つ時間を無駄にするよりもプロセッササイクルを使用する方が良いということです。



まず、三角関数を使用します。たとえば、 sqrt(sin*cos)



（これらはプロセッサを占有するための、最適でない形式の条件付き計算です）。



sqrt



、 sin



、およびcos



を使用します。これは、 sqrt



ごとに最大20個、三角関数ごとに最大100個を取ることができます。 この計算量は、メモリアクセス遅延をカバーできます。



チームの遅延の詳細については、Agner Foghによる優れたパフォーマンスガイドを参照してください。



ベンチマークコードは次のとおりです。 



 std::transform(std::execution::par, vec.begin(), vec.end(), out.begin(), [](double v) { return std::sqrt(std::sin(v)*std::cos(v)); } );


そして今何？ 以前の試みよりもパフォーマンスが向上することを期待できますか？



以下に結果を示します（ミリ秒単位の時間）：



運営 ベクターサイズ i7 4720（4コア） i7 8700（6コア）
実行:: seq 10k 0.105005 0.070577
実行::パー 10k 0.055661 0.03176
のopenmp並列 10k 0.096321 0.024702
実行:: seq 10万 1.08755 0.707048
実行::パー 10万 0.259354 0.17195
のopenmp並列 10万 0.898465 0.189915
実行:: seq 1000k 10.5159 7.16254
実行::パー 1000k 2.44472 1.10099
のopenmp並列 1000k 4.78681 1.89017


最後に、良い数字がいくつかあります:)



1000個の要素（ここには表示されていません）の場合、並列計算時間と順次計算時間は類似していたため、1000個を超える要素では、並列バージョンの改善が見られます。



10万個の要素の場合、高速なコンピューターでの結果は、シリアルバージョンのほぼ9倍です（OpenMPバージョンと同様）。



100万要素の最大バージョンでは、結果は5〜8倍高速です。

このような計算では、プロセッサコアの数に応じて「線形」加速を達成しました。 これは予想されることでした。



フレネルおよび3次元ベクトル



上記のセクションでは、「発明された」計算を使用しましたが、実際のコードはどうですか？

滑らかで平らな表面からの光の反射と曲率を記述するフレネル方程式を解きましょう。 これは、3Dゲームでリアルな照明を生成する一般的な方法です。









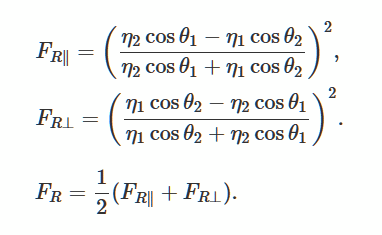
ウィキメディアからの写真



良い例として、 この説明と実装を見つけました。



GLMライブラリの使用について



独自の実装を作成する代わりに、glm libraryを使用しました 。 OpenGlプロジェクトでよく使用します。



ライブラリーはConan Package Managerを介して簡単にアクセスできるため、これも使用します。 パッケージへのリンク 。



コナンファイル： 



 [requires] glm/0.9.9.1@g-truc/stable [generators] visual_studio


ライブラリをインストールするコマンドライン（Visual Studioプロジェクトで使用できるpropsファイルを生成します）： 



 conan install . -s build_type=Release -if build_release_x64 -s arch=x86_64


ライブラリはヘッダーで構成されているため、必要に応じて手動でダウンロードできます。



実際のコードとベンチマーク



scratchapixel.comからglmのコードを適合させました： 



 //    https://www.scratchapixel.com float fresnel(const glm::vec4 &I, const glm::vec4 &N, const float ior) { float cosi = std::clamp(glm::dot(I, N), -1.0f, 1.0f); float etai = 1, etat = ior; if (cosi > 0) { std::swap(etai, etat); } //  sini     float sint = etai / etat * sqrtf(std::max(0.f, 1 - cosi * cosi)); //    if (sint >= 1) return 1.0f; float cost = sqrtf(std::max(0.f, 1 - sint * sint)); cosi = fabsf(cosi); float Rs = ((etat * cosi) - (etai * cost)) / ((etat * cosi) + (etai * cost)); float Rp = ((etai * cosi) - (etat * cost)) / ((etai * cosi) + (etat * cost)); return (Rs * Rs + Rp * Rp) / 2.0f; }


このコードは、プロセッサが実行することができるように、いくつかの数学命令、スカラー積、乗算、除算を使用します。 doubleベクトルの代わりに、4つの要素のベクトルを使用して、使用されるメモリの量を増やします。



ベンチマーク： 



 std::transform(std::execution::par, vec.begin(), vec.end(), vecNormals.begin(), //   vecFresnelTerms.begin(), //  [](const glm::vec4& v, const glm::vec4& n) { return fresnel(v, n, 1.0f); } );


結果は次のとおりです（ミリ秒単位）：



運営 ベクターサイズ i7 4720（4コア） i7 8700（6コア）
実行:: seq 1k 0.032764 0.016361
実行::パー 1k 0.031186 0.028551
のopenmp並列 1k 0.005526 0.007699
実行:: seq 10k 0.246722 0.169383
実行::パー 10k 0.090794 0.067048
のopenmp並列 10k 0.049739 0.029835
実行:: seq 10万 2.49722 1.69768
実行::パー 10万 0.530157 0.283268
のopenmp並列 10万 0.495024 0.291609
実行:: seq 1000k 08.2528 16.9457
実行::パー 1000k 5.15235 2.33768
のopenmp並列 1000k 5.11801 2.95908


「実際の」コンピューティングでは、並列アルゴリズムが優れたパフォーマンスを提供することがわかります。 2台のWindowsマシンでこのような操作を行うと、コアの数にほぼ線形に依存する高速化が実現しました。



すべてのテストで、OpenMPと2つの実装（MSVCとOpenMPが同様に機能する）の結果も示しました。



おわりに



この記事では、並列コンピューティングと並列アルゴリズムを使用する3つのケースを検討しました。 標準アルゴリズムをstd :: execution :: parバージョンに置き換えることは非常に魅力的に思えるかもしれませんが、これは常に行う価値があるとは限りません！ アルゴリズム内で使用する各操作は異なる動作をする場合があり、プロセッサまたはメモリにより依存します。 したがって、各変更を個別に検討してください。



覚えておくべきこと：





この記事を支援してくれたJFTに感謝します！



並列アルゴリズムに関する他の情報源にも注意してください：





並列アルゴリズムに関連する別の記事をご覧ください： Intel Parallel STLとC ++ 17並列アルゴリズムでパフォーマンスを向上させる方法



終わり



私たちはコメントや質問を待っています。それらはここか開いているドアの 先生に残すことができます。


More articles:


All Articles