ビットコインアドレスは、楕円曲線に基づいた暗号署名関数ECDSA()によって計算されます。
したがって、秘密鍵からビットコインアドレスを生成することを検討してください。
秘密鍵d-番号
公開鍵Qは、dGに等しい楕円曲線の点です。
ここで、Gは曲線の基点です。
- 署名の場合、範囲[1、n-1]で乱数kが選択されます。
- 曲線のポイントが計算されます(x1、y1)= k * G
- r = x1 mod Nを計算します。Nは曲線の次数です。
- s = k-1(H(m)+ rd)mod Nを計算します。ここで、k-1はNからk modulo Nの逆数です。
- H(m)は署名されるメッセージのハッシュです。
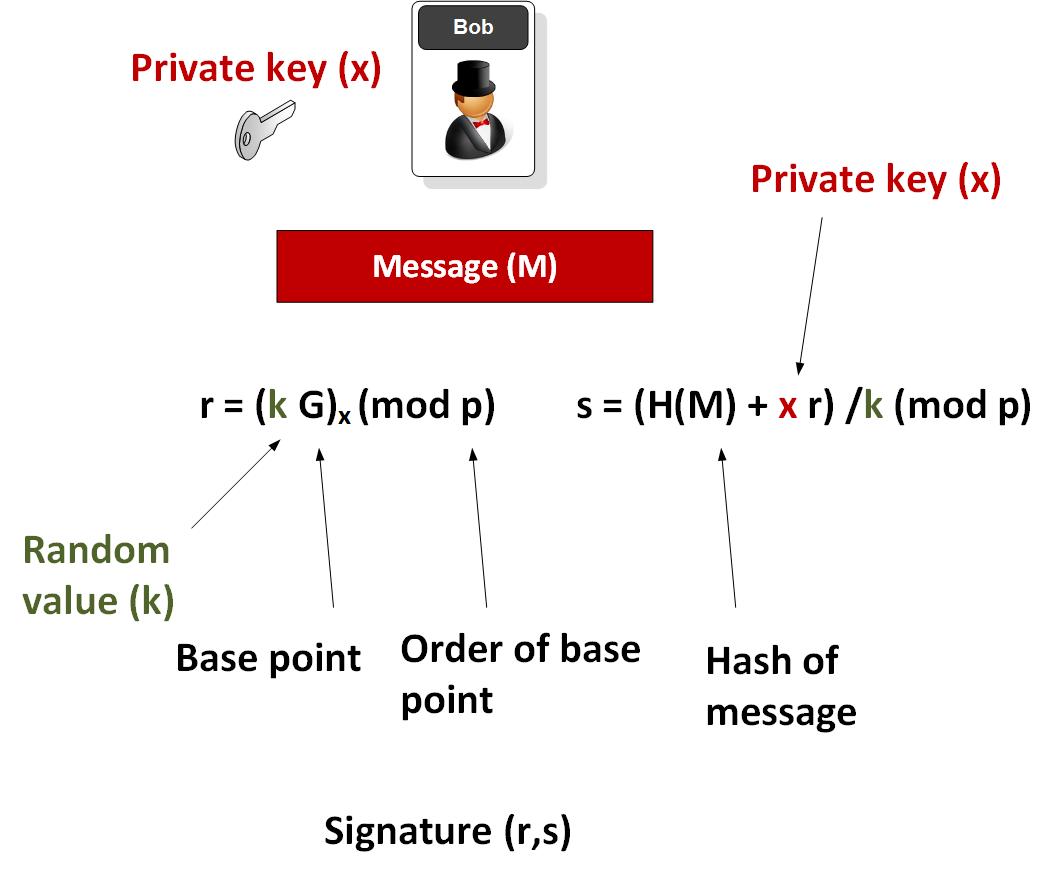
署名はペア(r、s)です。
変数「k」はランダムであり、オペレーティングシステムの標準ライブラリからECDSAアルゴリズムで取得されます。
したがって、関数全体では、この変数のみに影響を与えることができます。 これにより、2つの攻撃ベクトルが得られます。
- 擬似乱数の脆弱性
- 乱数が2回落ちる普遍的な運
擬似乱数ジェネレーター攻撃
Nils Schneiderは、2013年1月28日に個人ページでこの問題を調査して公開した最初の人物です。 しかし、問題は持続し、さらに新しい次元を獲得しました。
PRNGに対するソフトウェア攻撃は、3つのタイプに分類されます。
アルゴリズムの出力の分析に基づく直接暗号攻撃。
入力データに基づく攻撃は、既知の入力データによる攻撃、再現可能な入力データによる攻撃、および選択した入力データに対する攻撃に分類できます。
攻撃者がジェネレーターの初期または初期状態を知っている内部状態を明らかにすることに基づく攻撃。
また、ソフトウェアのブックマークも含まれています。このブックマークでは、アルゴリズムの作成者が、ハッシュ化された擬似乱数とチェーン内の後続の乱数のいずれかを認識しています。 このようなアルゴリズムは、数値が範囲全体に均等に分布しているように見えるため、外部から判断するのは困難です。
ソフトウェアの脆弱性には、個々のライブラリでの擬似乱数の弱い生成も含まれます。 SSL、OpenSSL、一部のJavaライブラリ、JavaScriptなど。 ハッキングの定期刊行物には詳細な資料が繰り返し記載されており、やがて暗号教科書の例になりました。
ビットコインの脅威の規模は?
完全なBitcoinノードを使用すると、すべてのネットワークトランザクションを比較およびグループ化できます。 各アドレスのすべてのトランザクションで変数「k」を比較し、重複を見つけるだけで十分です。
2016年の終わりに初めて調整を行ったとき、データベースのアドレスは2億1,000万を超え、トランザクションは合計で1億7000万を超え、署名は4億4,700万でした。 脆弱なアドレスを10個のスレッドにスキャンするのに1週間かかりました。
その結果、同じシグネチャを持つ1327の脆弱なアドレスが見つかりました! 住所のリストは記事の最後にあります。
これは、これらのアドレスへの秘密鍵を計算できることを意味します。つまり、お金を管理できます。
最大のリークは2015年の夏に発生しました。 JavaScriptウォレットBlockchain.infoが数時間にわたって変数「k」の同じ値を生成しました。 これにより、約200ビットコインが盗まれました!
ソフトウェアの脆弱性のヒューマンファクターを削除すると、偶然の可能性は約0.000296868%です。 それほど多くはありませんが、本当に「幸運」になり、お金を失いたくありません。
これに対処する方法は?
上で説明したように、この脆弱性は、支払いを送信し、少なくとも2つのトランザクションで同じ変数「K」を生成する場合にのみ機能します。 したがって、発信トランザクションを作成しないか、その数を最小化しない場合、脅威はまったくありません。 このような考え方は、ビットコインプロトコルBIP 32(階層的確定的ウォレット、HDウォレット)階層的確定的ウォレットで長い間実装されてきました。
彼のアイデアは、ビットコインアドレスの無限のチェーンを取得できる秘密鍵を使用することです。 1回限りのアドレスを使用して、個々のトランザクションを受信できます。 同時に、HDウォレットの残高は、アドレスチェーンのすべての残高の合計です。 また、送信トランザクションでは、これらのアドレスからコインが収集され、ビットコインアドレスごとに1つの送信トランザクションが作成されます。 変更は、アドレスチェーンから新しいビットコインアドレスに送信されます。
このような操作スキームにより、ウォレットのセキュリティと匿名性が大幅に向上します。
参照:
[1] ECDSA-アプリケーションおよび実装の失敗、Markus Schmid、UC SANTA BARBARA、CS 290G、2015年秋。
[2] Nils Schneider:ブロックチェーンからの弱い署名を使用したビットコイン秘密鍵の回復、ブログエントリ、2013年1月28日。
[3] 秘密鍵復旧の組み合わせ攻撃
[4] 脆弱なアドレスと全体的なバランスのリスト