主要な数学的成果は、研究者の小さなチームによって発見されたツィマー仮説でした。

対称性の高い次元の回折格子の場合、ランク以下の測定値に常に転送できるとは限りません
ロバート・ジマーの成功は多くの方法で定義できます。 2006年からシカゴ大学の学長を務めた彼は、9桁の資金を調達し、キャンパスでの言論の自由を支援する記事を公開するという見出しを見出しました。 しかし、大学の学長になる前は、数学者でした。 そして、彼が真剣な研究を去ってからずっと経って、彼が立ち上げた研究計画がついに結果を出した。
1年前、3人の数学者が 、幾何空間に特定のタイプの対称性がある状況に関連するジマーの仮説を証明しました 。 彼らの証明は、近年最大の数学的成果の一つとなっています。 1970年代後半から1980年代初頭の激しい精神活動中にジマーの前に生じた疑問を終わらせます。
「私は毎晩この仕事について考えながら5年間寝たと言っているので、それに夢中になりました。人々がそれを解決する方法を見るのは素晴らしいことです」とジマーは言いました。
通常、幾何学的な次元空間が大きいほど、より多くの対称性が存在できます。 これは、2次元平面上に存在する円と3次元に広がるボールを調べることで想像できます。ボールを回転させる方法は、円を回転させる方法よりも多くあります。 追加のボール寸法により、追加の対称性が作成されます。
Zimmerの予想は、高ランク格子として知られる特別な種類の対称性を指します。 彼女は、幾何空間の測定がこのタイプの対称性の使用を制限するかどうかを尋ねます。 新作の著者であるシカゴ大学のアーロン・ブラウンとセバスチャン・ウルタド・サラザール 、インディアナ大学のデビッド・フィッシャーは、特定の対称性よりも少ない測定数では観測されないことを示しました。 したがって、彼らはジマーの仮説の正しさを証明した。

現在シカゴ大学の学長であるロバート・ジマーは、ほぼ40年前に彼にちなんで命名された仮説を立てました
彼らの仕事は、他の多くの研究の新しい方法を切り拓く、1つの重要で長年の質問に答えます。 また、幾何空間の固有の特性も明らかにします。 対称性は、そのような空間の最も単純な特性の1つです。 新しい作品は、対称性があるタイプの空間に存在し、他のタイプの空間には存在できないと述べています。 この成果は、数十年のダウンタイムの後に達成されました。
「この仮説は、人々を非常に長い間忙しくさせることができるように思われた」と、この証明について今年の会議を開催したシカゴ大学の数学者、エイミー・ウィルキンソンは述べた。 「そして、彼らはこの質問を比較的単純に破壊した。」
満足のいく対称性
対称性は、子供たちが数学で出会う最初の幾何学的概念の1つです。 彼らは自分の手で、フォームを回転、反転、シフトし、最終的には開始時と同じフォームを取得できることを学びます。 変更の結果としてオブジェクトの形状を維持すると、特定の内部満足度で応答します。これは、宇宙に深い秩序が存在することのヒントです。
数学者には、対称性を研究するための独自の形式言語があります。 与えられた幾何空間で適用可能なさまざまな対称性について簡潔に議論する機会を彼らに与えます。
たとえば、正方形には8つの対称性があり、8つの方法でそれを反転または回転させ、再び正方形を取得します。 円は任意の角度で回転できます。 彼女には無限の対称性があります。 数学者は、指定された幾何学的オブジェクトまたは空間のすべての対称性を収集し、それらを「グループ」にまとめます。
グループはそれ自体興味深いものです。 それらは特定の幾何学的空間の研究の結果としてしばしば現れるが、時には幾何学的に完全に無関係な文脈で現れる。 たとえば、グループは数値セットを形成できます(たとえば、数値から5を加算したり、5を減算したりする対称性があります)。
「グループは、原則として、まったく異なるものの対称性として現れる可能性があります」とジマーは言いました。
学校で勉強しているものよりもエキゾチックな形の対称性があります。 たとえば、格子の対称性を考えてみましょう。 最も単純な格子は、2次元のグリッドです。 平面上で、ラティスを任意の数の正方形だけ上下左右にシフトし、元のラティスとまったく同じように見えるラティスを取得できます。 任意の数の個々のセルを通してグリッドを反映することもできます。 格子のある空間には、無限の数の異なる格子の対称性があります。
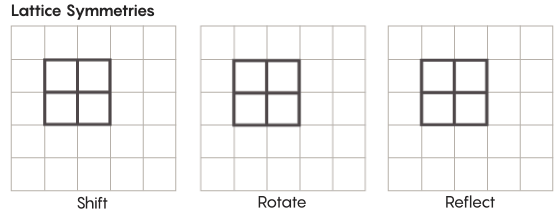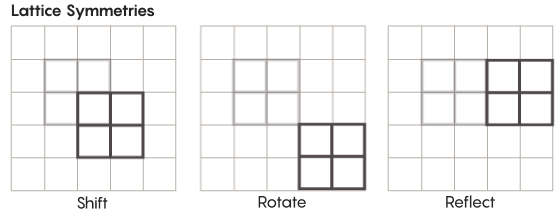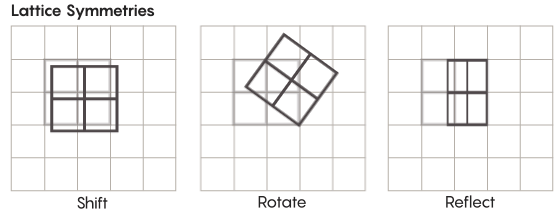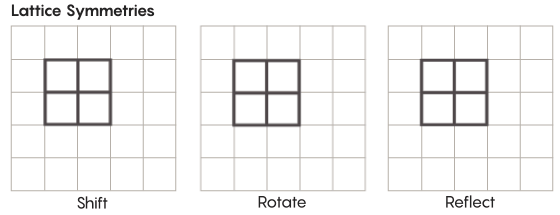
格子は、任意の数の次元に存在できます。 3次元空間では、格子は正方形ではなく立方体で構成されます。 4次元以上では、格子を表示することはできませんが、同じように機能します。 数学者はそれを正確に説明できます。 Zimmer仮説の対象グループには、「上位ランク」格子、または高次元の特定の空間内の格子が含まれます。 「この奇妙な格子は、たとえそれが私に与えられなくても、見ることができれば非常に美しいだろう」とフルタド・サラザールは言った。 「彼女を見ることはとてもいいことだと思う。」
20世紀に、数学者はさまざまな条件下でこれらのグループを発見しました-幾何学だけでなく、数論、論理学、およびコンピューターサイエンスでも。 新しいグループを開いて、質問をするのは論理的です-どのようなスペースがそのような対称性のセットを持っていますか?
グループをスペースに合わせることが明らかに不可能な場合があります。 円の対称性のグループは正方形に適用できないことをすぐに理解できます。 正方形を10度回転すると、元の正方形は得られません。 しかし、無限数の対称性を持つグループと多くの次元を持つ空間が混在すると、グループの適用可能性を判断するのが難しくなります。
「より多くの次元でより複雑なグループに移行する場合、これらの問題は非常に複雑になります。」
間接接続
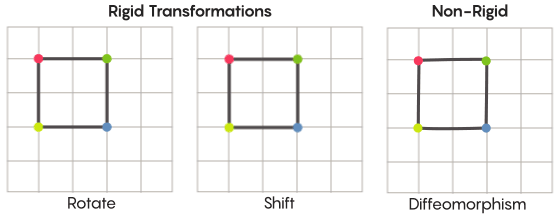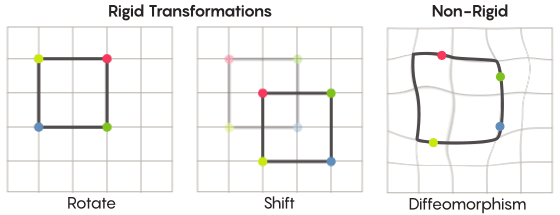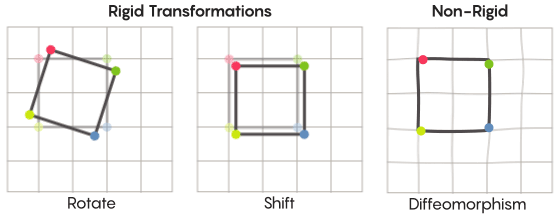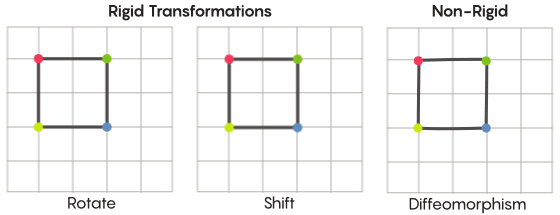
対称性を想像して、フォーム全体の回転を想像してください。たとえば、正方形が90度回転していることです。 しかし、基本的なレベルでは、対称性は移動ポイントに依存します。 空間の対称変換は、空間のすべてのポイントを取得し、他のポイントに移動する必要があることを意味します。 この意味で、正方形を90度回転させるということは、実際には正方形の各点を取り、それを90度回転させて、開始点から離れないようにする必要があることを意味します。

デビッド・フィッシャー
ポイントの移動の問題は、多少厳密に解決できます。 最もよく知られている対称変換-対角線に対する正方形の反射または90度の回転-は非常に厳密です。 ポイントを混同しないという意味で厳格です。 反射前の頂点であったポイントは、後の頂点のままであり(他の頂点になります)、反射後の直線エッジを構成するポイントは、依然として直線エッジを構成します(異なる)。
それほど厳密ではなく、より柔軟なタイプの対称変換があり、Zimmer仮説のコンテキストでは興味深いものです。 このような変換では、ポイントが組織をより強く変更します。 変換後、必ずしも以前の接続を保持しているわけではありません。 たとえば、正方形の各ポイントを正方形の周囲に沿って3単位の長さだけ移動できます。これは、対称変換の基本要件を満たします。つまり、単に空間内の各ポイントを別の場所にシフトします。 証明の共著者であるアーロン・ブラウンは、これらのより自由に見える変換がボールのコンテキストでどのように見えるかを説明しました。
「北極と南極を取り、それらを反対方向にねじることができます。 すると、ポイント間の距離が長くなります」とブラウンは言います。
グリッドの場合、平面に沿って単純に移動するのではなく、変形したメッシュが元のメッシュと重ならないように、ある場所で曲げたり、伸ばしたり、絞ったりすることができます。 このような変換はそれほど厳密ではなく、 微分同相写像と呼ばれます。
ジマーは、彼の仮説で対称性のこのそれほど厳密でないバージョンを使用する正当な理由がありました。 この仮説に関連する最高ランクの特別な格子は、1960年代に、彼の研究でフィールズ賞を受賞したGrigory Alexandrovich Margulisによって最初に研究されました。 マルグリスは、厳密な変換のみが許可されている場合、これらの上位格子を使用してどのような空間を変換できるかについて完全な説明を行いました。
ジマーの仮説は、マルグリスの仕事の自然な継続となった。 最上位のラティスが機能するスペースのリストから始まります-マルグリスはこのリストを発見しました-ラティスがより厳密でない変換を許可されている場合、このリストが拡張されているかどうかを尋ねます。
新しい研究では、3人の数学者が対称性の定義を弱めても高次格子の対称性の範囲を変えないことを証明しました。 ラティスが非常に不規則な変換(シフト、ベンド、ストレッチ)を許可されている場合でも、ラティスにはスコープに対する厳しい制限があります。
「問題のステートメントにこのような柔軟性を追加した後、もちろん直感的に、グリッドはより広く機能するように思われます。 したがって、実際には答えが「いいえ」になることは驚くべきことになります-場合によってはできない、とフィッシャーは言いました。
数学者は、与えられた空間で対称の役割を果たすことができる格子について、空間の次元と格子の次元またはランクの間の正確な対応を確立しました。 一般に、彼らは、格子のランクが高いほど、それを収容できるスペースにより多くの測定が必要であることを示しました。 空間の変換にかなりの柔軟性があったとしても、高ランクの格子の変換は高次元に制限されます。
「これは、空間の構造に非常に基本的なものがあることを示唆しており、そのような変換に対応する能力を意味します」とウィルキンソンは言いました。
Zimmerの仮説は、より大きなプログラムへの最初のステップにすぎません。 それに対処した後、この研究の共著者は、上位の格子を変換できる空間に大きな制限を課しました。 仕事の次の、より野心的な段階は、格子が存在できるそれらの空間への集中であり、そしてこれらの空間の格子を変換するすべての異なる方法の分類です。
「最終的に、プログラムはこれらすべてのメソッドを分類できるはずです。 グリルが作動できない特定の場所が存在するという事実の単純な確立を超えて、多くの興味深い質問があります」とZimmerは述べました。