PS。この記事には、habrエディターマクロによって追加された数式が含まれています。 彼らは時々表示されないと言います。 gif形式のアニメーションも多数あります。
前文
数学的最適化の問題は、「セットで検索」という形式の問題です。 要素 そのような から 行った 「、科学文献では、このように書かれている可能性が高い
歴史的に、勾配降下法やニュートン法などの一般的な方法は線形空間でのみ機能します ) 実際には、線形空間にない最小値を見つける必要があるという問題がしばしばあります。 たとえば、このようなベクトルの関数の最小値を見つける必要があります そのために 、これは次の事実による可能性があります オブジェクトの長さを示します。 または、たとえば、 以下でなければならない点の座標を表します から つまり 。 このような問題の場合、勾配降下法またはニュートン法は直接適用できなくなりました。 最適化の問題の非常に大きなクラスは、上記で説明したものと同様に、「制限」によって便利にカバーされることが判明しました。 つまり、セットを表すと便利です 平等と不平等のシステムの形で
フォームのスペース上の最小化問題 したがって、彼らは慣習的にそれらを「制約のない問題」と呼び始め、等式と不等式のセットによって定義されたセットに関する問題は「制約のある問題」と呼ばれました。
技術的には、絶対に多数 インジケーター -functionを使用して、単一の等式または不等式として表すことができます。
ただし、このような関数にはさまざまな有用なプロパティ(凸性、微分可能性など)がありません。 しかし、しばしば想像することができます いくつかの等式と不等式の形で、それぞれにそのような特性があります。 基本的な理論は、ケースの下で要約されています
どこで -凸関数(必ずしも微分可能ではない)関数、 -マトリックス。 メソッドがどのように機能するかを示すために、2つの例を使用します。
- 線形計画法タスク
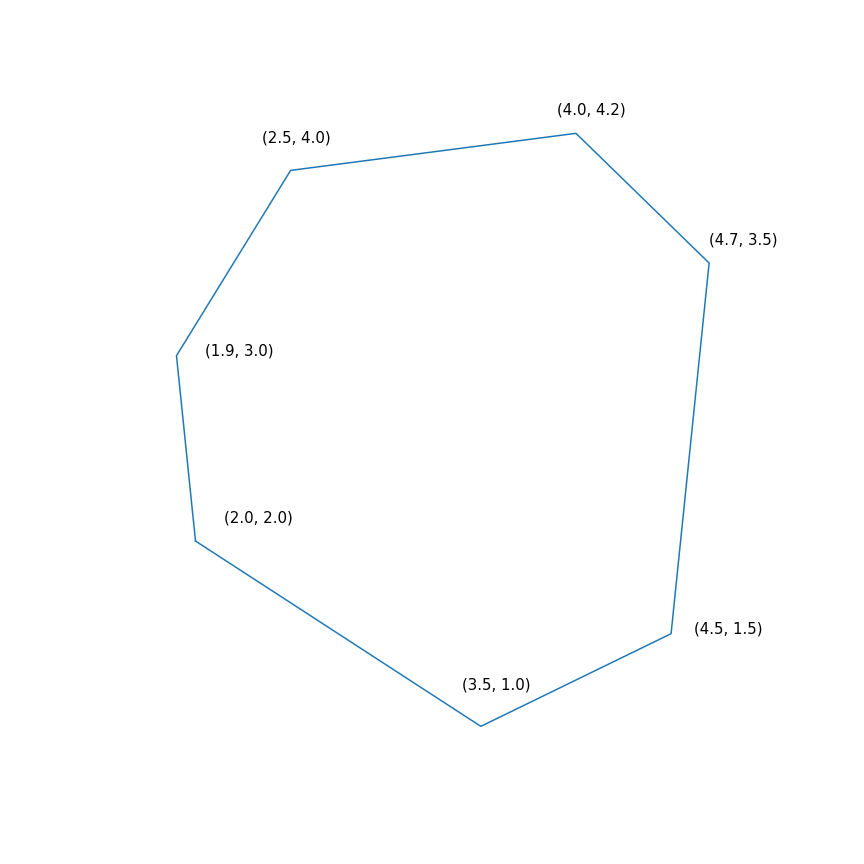
$$ display $$ \ begin {array} {rl} \ mbox {minimize}&-2&x ~~~-&y \\ \ mbox {provided}&-1.0&〜x -0.1&〜y \ leq -1.0 \ \&-1.0&〜x +〜0.6&〜y \ leq -1.0 \\&-0.2&〜x +〜1.5&〜y \ leq -0.2 \\&〜0.7&〜x +〜0.7&〜y \ leq 0.7 \\&〜2.0&〜x -0.2&〜y \ leq 2.0 \\&〜0.5&〜x -1.0&〜y \ leq 0.5 \\&-1.0&〜x -1.5&〜y \ leq- 1.0 \\ \ end {array} $$表示$$
本質的に、この問題は方向(2、1)でポリゴンの最も遠い点を見つけることにあり、問題の解決策は点(4.7、3.5)-ポリゴンの最も「正しい」)です。 しかし、ポリゴン自体
- 1つの2次制約を持つ2次関数の最小化
シンプレックス法
このレビューで取り上げたすべての方法の中で、おそらくシンプレックス法が最も有名です。 この方法は線形計画法のために特別に開発され、提示されたもののうちの1つが有限数のステップで正確な解を達成します(計算に正確な算術が使用される場合、実際には通常そうではありませんが、理論的には可能です)。 シンプレックス法のアイデアは、2つの部分で構成されています。
- 線形不等式と等式のシステムは、多次元凸多面体(多面体)を定義します。 1次元の場合は点、光線、またはセグメントであり、2次元の場合は凸多角形、3次元の場合は凸多面体です。 線形関数を最小化することは、本質的に特定の方向の「最も遠い」点を見つけることです。 直観は、この最も遠い点が特定のピークであるべきだと示唆するべきだと思います。これは確かにそうです。 一般的に、システムの 不等式 次元空間頂点は、システムを満たす点であり、 これらの不平等の平等になります(ただし、不平等には同等なものはありません)。 そのようなポイントの数は常に多くなりますが、常に有限数です。
- 現在、有限のポイントセットがあり、一般的に言えば、単純にそれらを選択して並べ替えることができます。つまり、次のようなことを行います。 不等式により、選択した不等式でコンパイルされた線形方程式系を解き、解が元の不等式系に適合することを確認し、他のそのような点と比較します。 これは非常に単純ですが、非効率的ですが機能する方法です。 シンプレックス法は、反復する代わりに、目的関数の値が改善されるように、エッジに沿って上から上に移動します。 頂点に、関数の値がより良い「隣接」がない場合、最適であることがわかります。
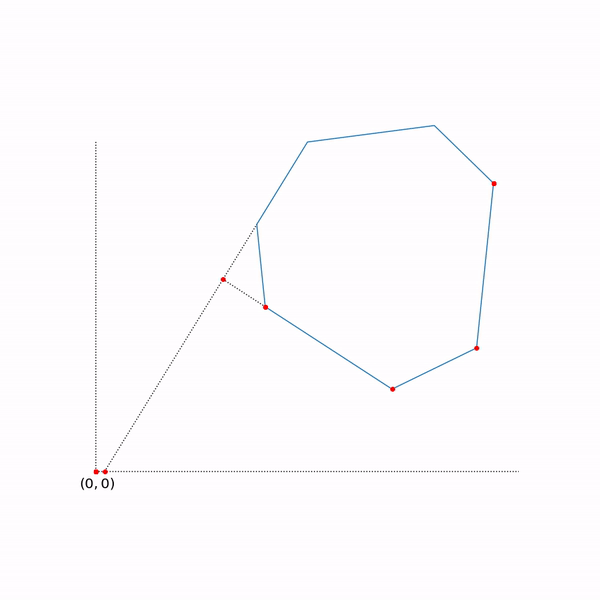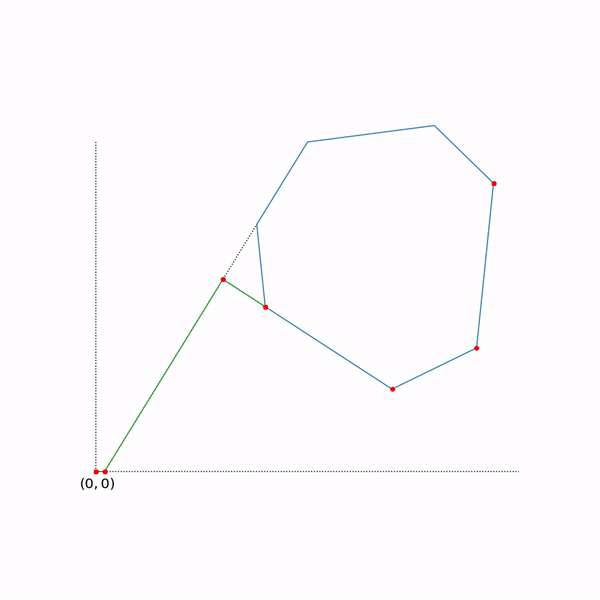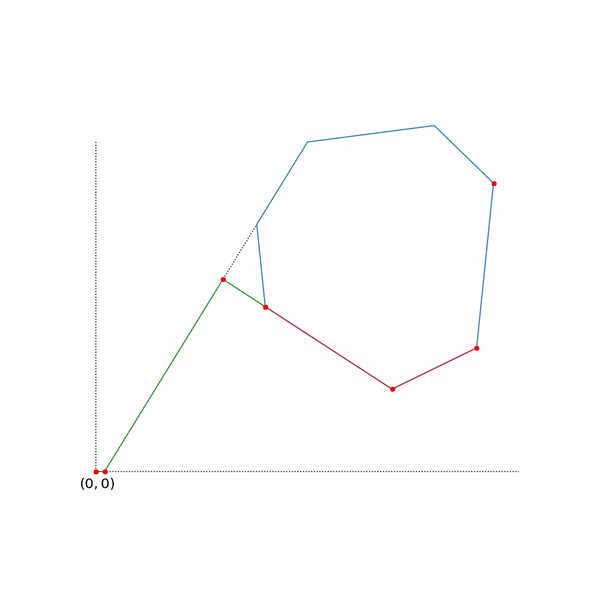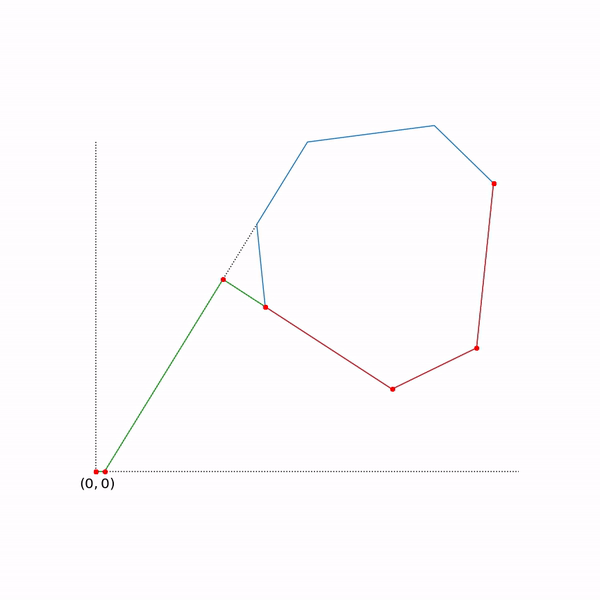
シンプレックス法は反復的です。つまり、逐次的にソリューションが少し改善されます。 そのような方法では、どこかから始める必要があります。一般的な場合、これは補助的な問題を解決することによって行われます
この問題を解決する場合 そのような その後実行 それ以外の場合、元の問題は通常、空のセットで与えられます。 補助的な問題を解決するには、シンプレックス法を使用することもできますが、開始点をとることができます 任意で 。 開始点を見つけることは任意にメソッドの第1フェーズと呼ばれ、元の問題の解を見つけることは任意にメソッドの第2フェーズと呼ばれます。
二相シンプレックス法の軌跡
軌道は、scipy.optimize.linprogを使用して生成されました。

射影勾配降下
勾配降下について、私は最近、別の記事を書き、この方法についても簡単に説明しました。 現在、この方法は非常に活発ですが、より一般的な近位勾配降下の一部として研究されています。 この方法のアイデアは非常に平凡です:勾配降下を凸関数に適用すると 、パラメータの正しい選択により、グローバルな最小値を取得します 。 勾配降下の各ステップの後に、得られた点が修正され、代わりに閉じた凸集合への投影が行われる場合 、その後、結果として関数の最小値を取得します に 。 まあ、またはより正式には、射影勾配降下法は逐次計算するアルゴリズムです
どこで
最後の等式は、セットへの射影の標準演算子を定義します。実際、それは、ポイントに従って、 セットに最も近い点を計算します 。 ここで距離の役割が果たす 、ここで任意のノルムを使用できることに注意してください。ただし、異なるノルムの投影法は異なる場合があります。
実際には、射影勾配降下法は特別な場合にのみ使用されます。 その主な問題は、投影の計算が元の投影よりもさらに難しくなる可能性があり、何度も計算する必要があることです。 射影勾配降下法を使用するのが便利な最も一般的なケースは、次の形式の「ボックス制限」です。
この場合、投影は非常に簡単に計算され、座標ごとに判明します
線形計画問題に射影勾配降下法を使用することはまったく意味がありませんが、すべて同じように実行すると、次のようになります。
線形計画問題の射影勾配降下軌道 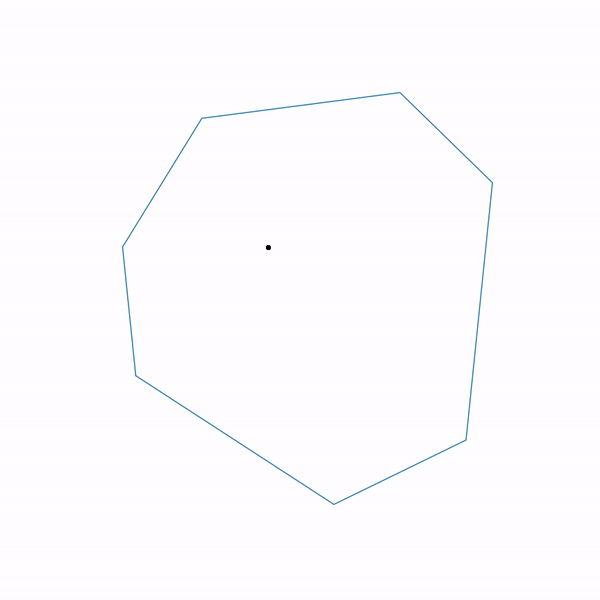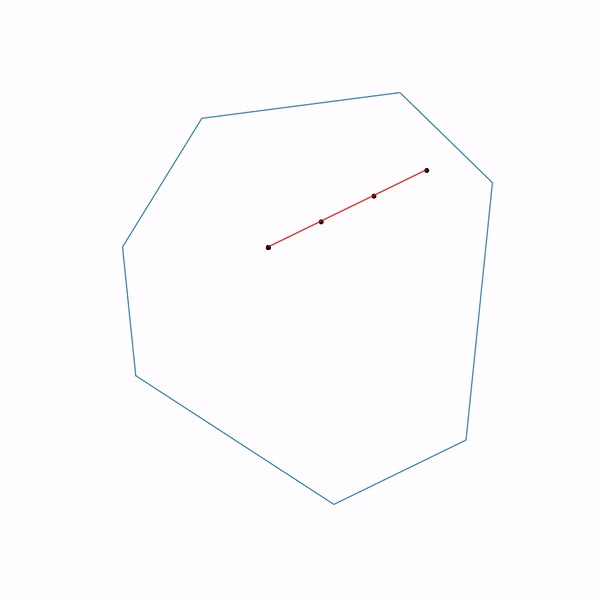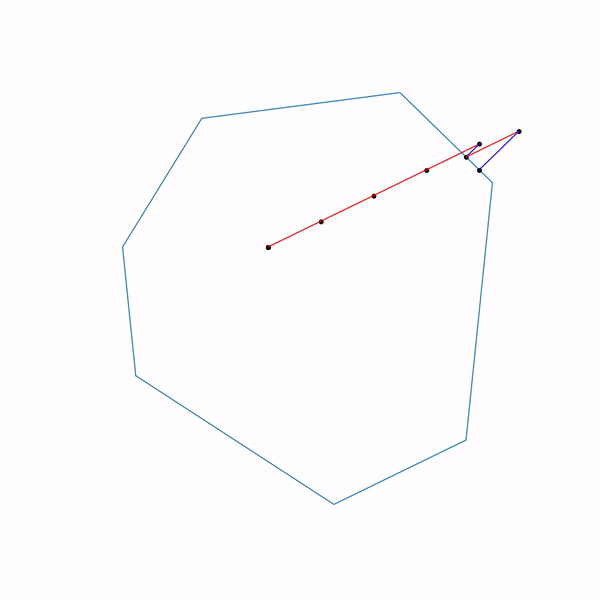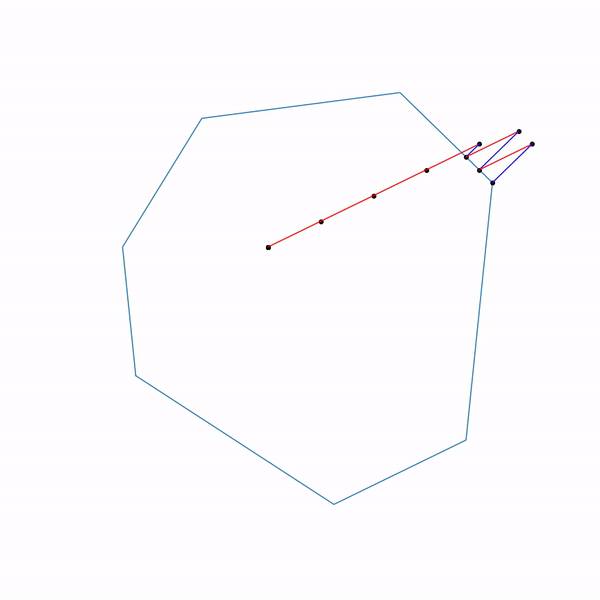

そして、2番目の問題の射影勾配降下の軌跡は次のとおりです。
大きなステップサイズを選択する 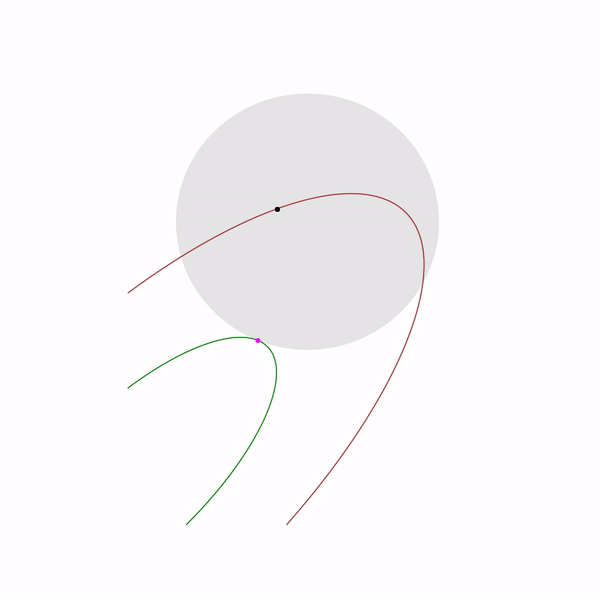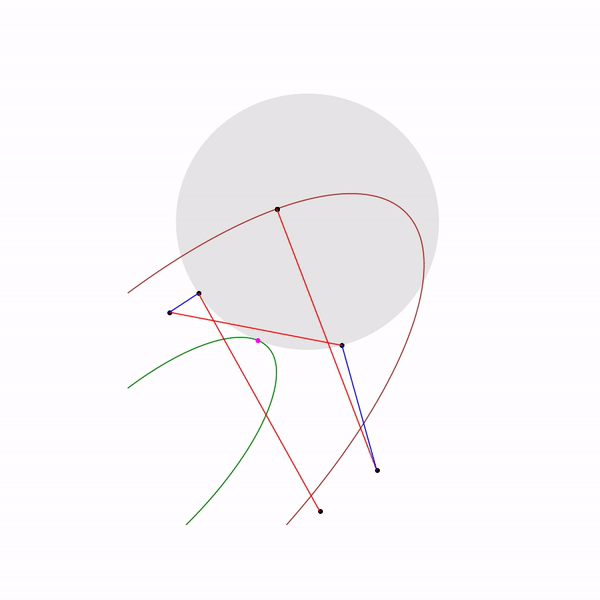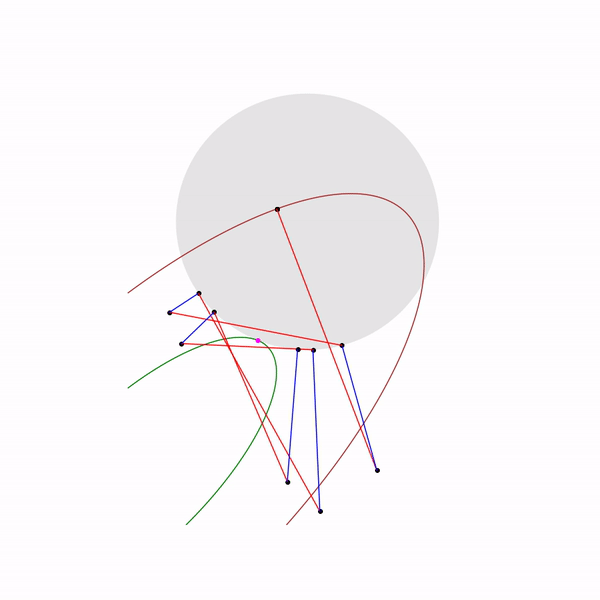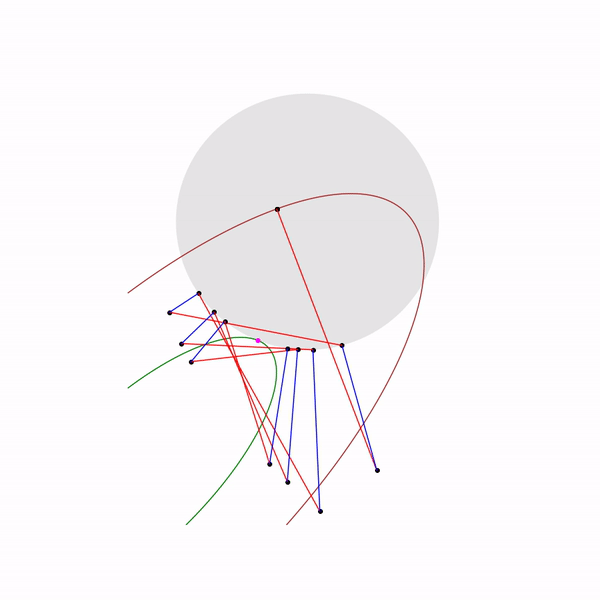

そして
小さなステップサイズを選択してください 

楕円法
この方法は、線形計画問題の最初の多項式アルゴリズムであるという点で注目に値します; 二分法の多次元一般化と考えることができます。 超平面を分離するより一般的な方法から始めます。
- メソッドの各ステップには、問題の解決策を含むセットがあります。
- 各ステップで、超平面が構築され、その後、選択された超平面の片側にあるすべてのポイントがセットから削除され、いくつかの新しいポイントがこのセットに追加されます
最適化問題の場合、「分離超平面」の構築は、凸関数の次の不等式に基づいています
修正する場合 、次に凸関数の場合 半分のスペース ポイント以上の値を持つポイントのみを含む 、つまり、これらのポイントは既に見つけたものよりも優れていないため、それらを切り捨てることができます。 制限の問題についても、制限の1つに違反することが保証されているポイントを同様に取り除くことができます。
分離超平面法の最も単純なバージョンは、点を追加せずに単純に半空間を切り取ることです。 その結果、すべてのステップで特定の多面体ができます。 この方法の問題は、多面体の面の数が段階的に増加する可能性があることです。 さらに、指数関数的に成長する可能性があります。
楕円法は、各ステップで楕円を実際に保存します。 より正確には、超平面が構築された後、最小体積の楕円体が構築され、元の部分の1つが含まれます。 これは、新しいポイントを追加することで実現できます。 楕円体は、次のように常に正定行列とベクトル(楕円体の中心)で定義できます。
半空間と別の楕円体の交点を含む体積の最小楕円体の構築は、 やや面倒な公式を使用して実行できます。 残念ながら、実際には、この方法はシンプレックス法または内部ポイント法と同じくらい優れていました。
しかし、実際にはそれがどのように機能するか
線形計画法 

そして
二次計画法 

内点法
この方法には開発の長い歴史があり、シンプレックス法が開発されたのとほぼ同時に最初の前提条件の1つが現れました。 しかし、当時は、実際に使用するにはまだ十分な効果がありませんでした。 1984年の後半に、この方法の変形が線形計画法のために特別に開発されました。これは理論と実践の両方で優れていました。 さらに、内部点法は、シンプレックス法とは異なり、線形計画法だけに限定されず、現在では制限のある凸最適化問題の主要なアルゴリズムです。
この方法の基本的な考え方は、制限をいわゆるバリア関数の形式の罰金に置き換えることです。 機能 セットのバリア関数と呼ばれる もし
ここに -内部 、 -ボーダー 。 元の問題の代わりに、問題を解決することが提案されています
そして 内側だけに与えられた (実際、これは名前の由来です)、バリアのプロパティにより、 少なくとも 存在します。 また、より インパクトが大きい 。 合理的に合理的な条件の下で、あなたが目指すならそれを達成することができます 無限大、最小 元の問題の解に収束します。
セットの場合 不等式のセットとして与えられる バリア関数の標準的な選択は対数バリアです
最小ポイント 機能 別の 通常は中央経路と呼ばれる曲線を形成しますが、内点法は、この経路をたどろうとします。 これはそれがどのように見えるかです
線形計画法の例 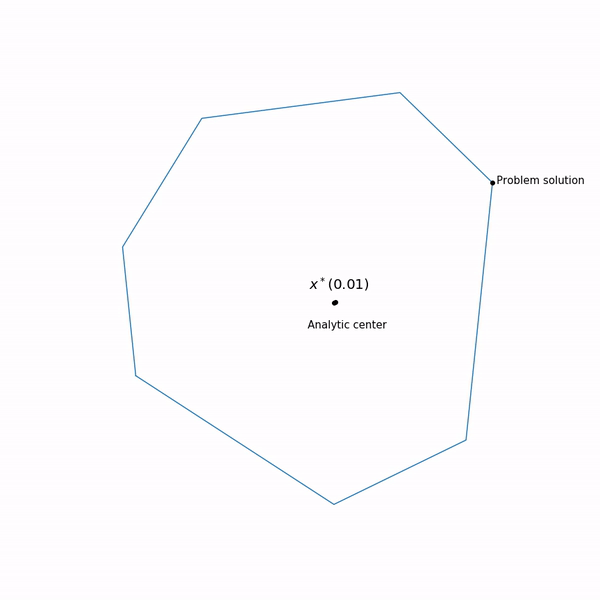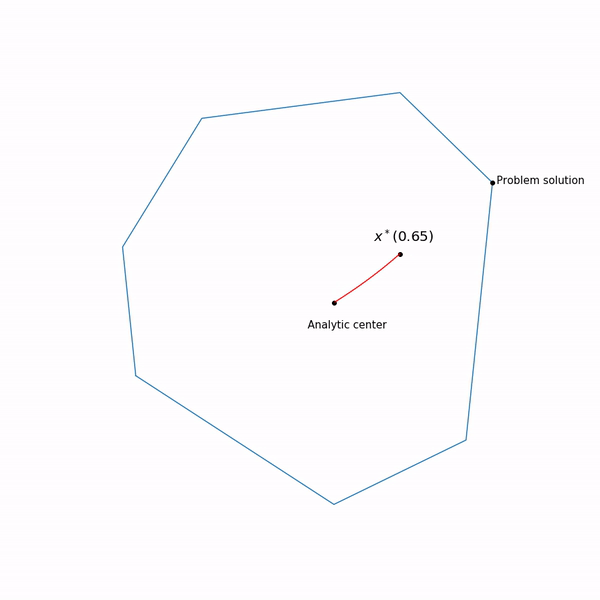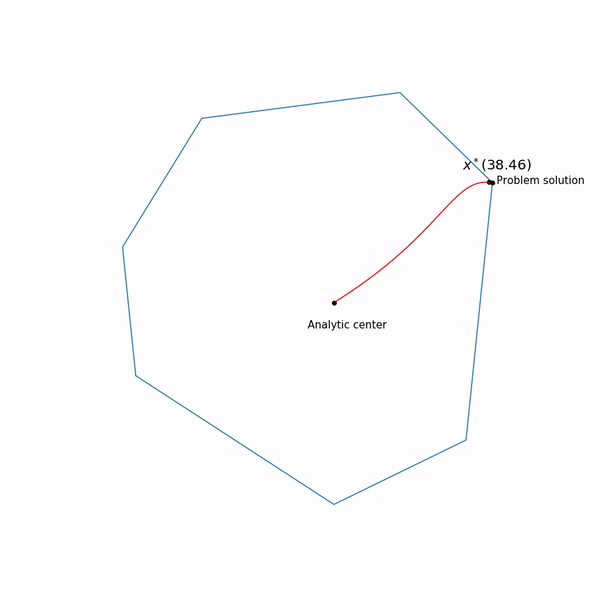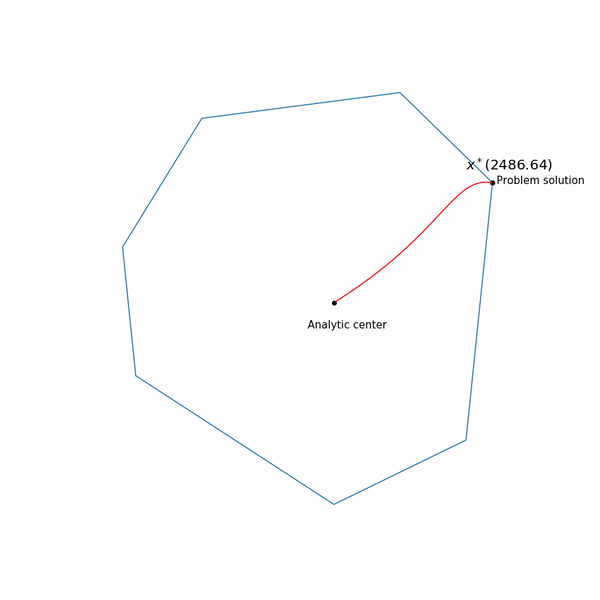
分析センターはただ

分析センターはただ
最後に、内部ポイントメソッド自体の形式は次のとおりです。
- 初期近似を選択する 、
- ニュートン法を使用して新しい近似を選択します
- クリックして拡大
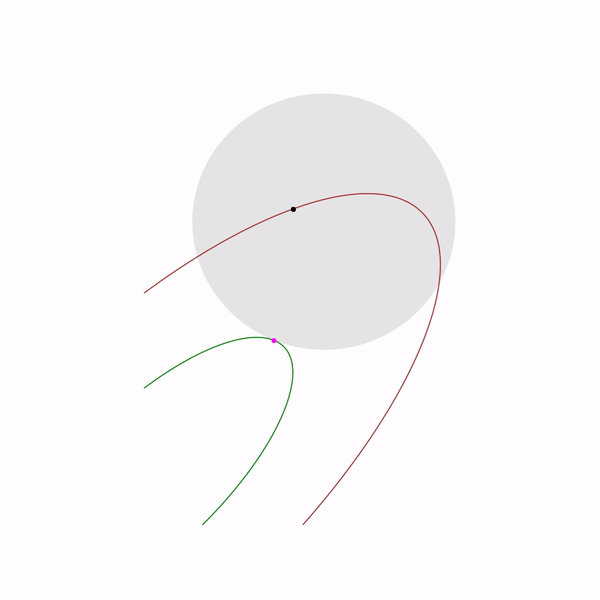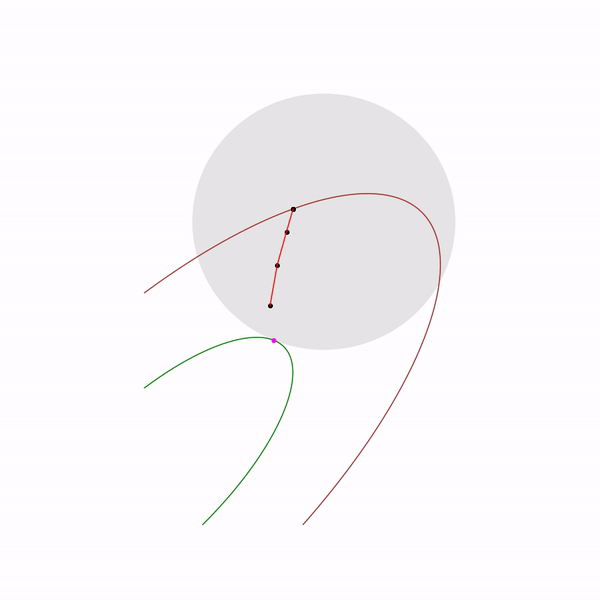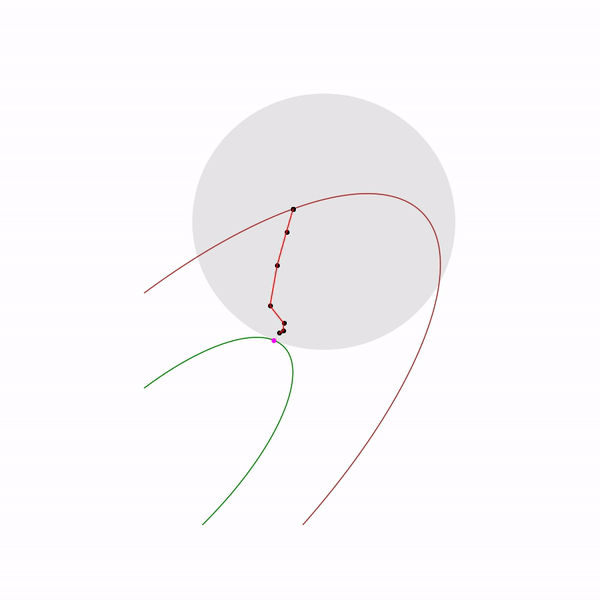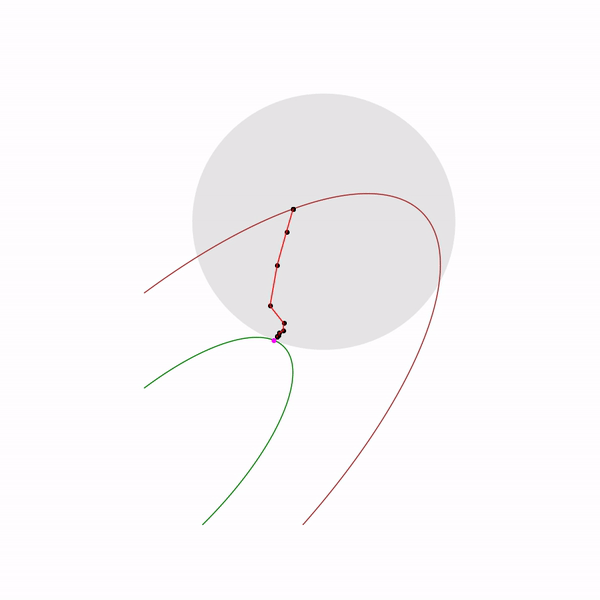
ここでのニュートン法の使用は非常に重要です:実際には、バリア関数の正しい選択により、ニュートン法のステップは
線形計画法タスク 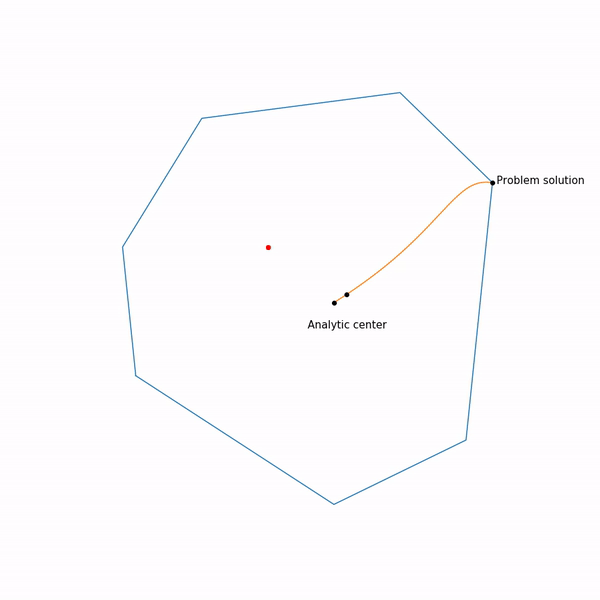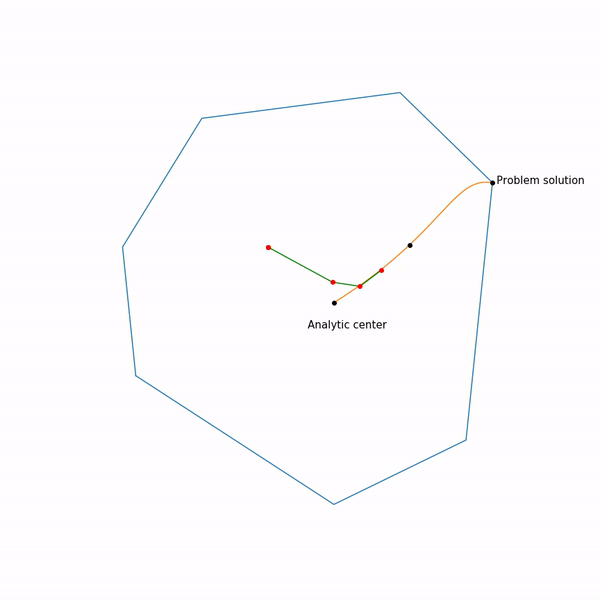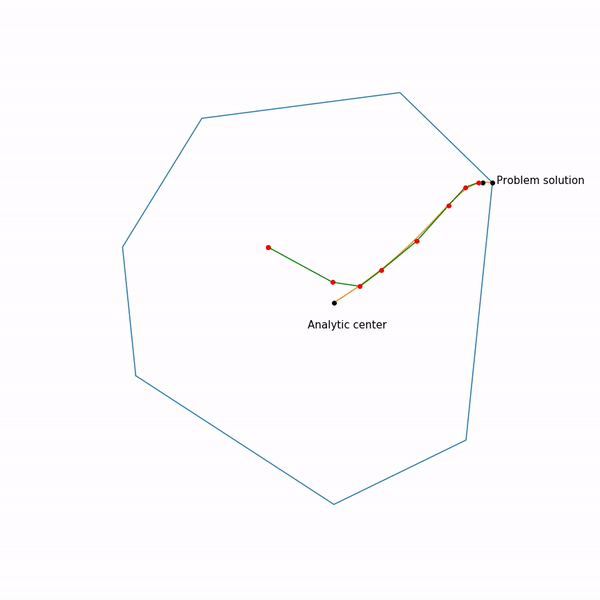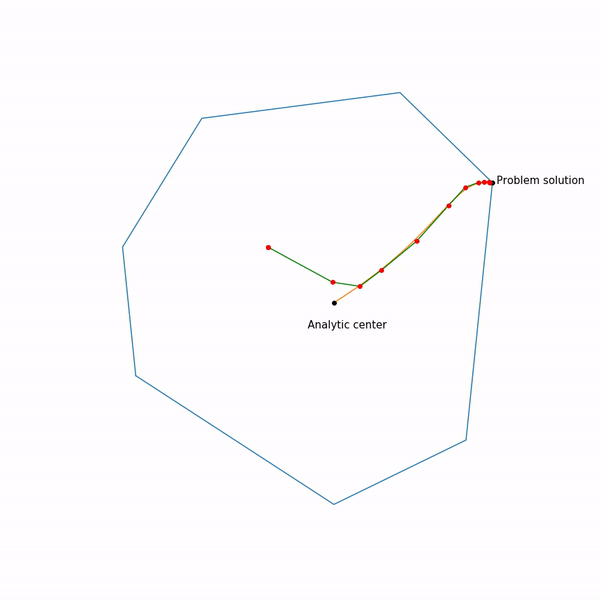
跳ねる黒い点は 、つまり 現在のステップでニュートン法のステップにアプローチしようとしているポイント。

跳ねる黒い点は 、つまり 現在のステップでニュートン法のステップにアプローチしようとしているポイント。
二次計画問題