1年半前、私は「指の数学：最小二乗法」という記事を公開しました。これは、特にフクロウを描くことを提案したという事実から成り立っています。 さて、フクロウなので、もう一度説明する必要があります。 1週間後、このテーマについて正確に、地質学の学生にいくつかの講義を開始します。 私はこの機会を利用して、ここで（適合した）主要な点をドラフトとして提示します。 私の主な目標は、おいしい健康的な食べ物に関する本から既製のレシピを提供することではなく、数学の異なるセクション間の接続が最も興味深いので、それがそうである理由と対応するセクションに他に何があるかを説明することです！



現時点では、次のようにテキストを分割するつもりです。

• 確率論に関する教育プログラム（紹介記事、オプション）
  
  
• 線形連立方程式の紹介
  
  
• 有限要素法
  
  
• 二次形式の最小化とOLS問題の例
  
  
• 最小二乗からニューラルネットワークへ
  
  

最尤法の原理を介して、最小二乗法を少し横に移動します。これには、確率論の方向性が最小限で済みます。 このテキストは、地質学部の3年目のために設計されています。つまり、（関係する機器の観点から！）適切な熱意を持った興味のある高校生はそれを理解できるはずです。

理論家はどのくらい健全ですか、または進化論を信じていますか？

ある日、進化論を信じるかどうか尋ねられました。 今すぐ一時停止し、どのように答えるかを考えてください。







個人的に、私は驚きました、私はそれが信じられると思うと答えました、そして、信仰の問題はここで全く生じません。 科学理論は信仰とはほとんど関係ありません。 要するに、理論は私たちの周りの世界のモデルを構築するだけであり、それを信じる必要はありません。 さらに、 ポッパーの基準では、反論できる科学的理論が必要です。 また、健全な理論には、まず第一に予測力が必要です。 たとえば、作物自体が農薬を生産するように作物を遺伝子組み換えした場合、作物に耐性のある昆虫が現れるのは論理的です。 しかし、通常の植物を遺伝子組み換え植物と並べて栽培することにより、このプロセスが遅くなる可能性はそれほど明白ではありません。 進化論に基づいて、対応するシミュレーションがそのような予測を行い 、 確認されたようです。

そして、最小二乗はそれと何の関係がありますか？

前に述べたように、最尤法を使用して最小二乗法に進みます。 例で説明しましょう。 ペンギンの成長に関するデータに関心があると仮定しますが、これらの美しい鳥のほんの一部しか測定できません。 成長分布モデルをタスクに導入することは非常に論理的です-ほとんどの場合、それは正常です。 正規分布は、平均値と標準偏差の2つのパラメーターによって特徴付けられます。 パラメーターの固定値ごとに、作成した測定値が正確に生成される確率を計算できます。 さらに、パラメーターを変化させることにより、確率を最大化するパラメーターを見つけます。



したがって、最尤法で作業するには、確率論の観点から操作する必要があります。 少し下の、指で、確率と尤度の概念を定義しますが、最初に別の側面に焦点を当てたいと思います。 驚くべきことに、「確率論」というフレーズの中で「理論」という言葉を考えている人はほとんどいません。

学習理論とは何ですか？

確率推定の起源、意味、範囲に関しては、100年以上にわたって激しい議論が続いています。 例えば、 ブルーノ・デ・フィネッティは、確率は何かが起こる確率の主観的分析に過ぎず、この確率は心の外には存在しないと述べました。 これは、起こっていることに賭ける人の意欲です。 この意見は、同じイベントが何度も繰り返される可能性があると想定されている特定の結果の確率に関する古典/フリーベントの見解と正反対であり、特定の結果の「確率」は、繰り返されるテスト中に特定の結果が落ちる頻度に関連しています。 主観主義者と熱狂主義者に加えて、確率は観測者の自信の程度の説明ではなく、宇宙の本当の側面であると主張する客観主義者もいます。



実際のところ、3つの科学学校はすべて、コルモゴロフの公理に基づいて同じ装置を使用しています。 コルモゴロフの公理に基づいて構築された、確率論を支持して、主観主義的な観点から間接的な議論をしましょう。 公理自体は少し後で説明しますが、最初は次のワールドカップに賭けるブックメーカーがあると仮定します。 2つのイベントがあります。a=ウルグアイのチームがチャンピオンになり、b =ドイツのチームがチャンピオンになります。 ブックメーカーは、ウルグアイのチームが勝つチャンスを40％、ドイツのチームが勝つチャンスを30％と見積もっています。 明らかに、ドイツとウルグアイの両方が同時に勝つことはできないため、a∧bのチャンスはゼロです。 同時に、ブックメーカーは、ウルグアイまたはドイツ（アルゼンチンまたはオーストラリアではない）が勝つ確率は80％であると考えています。 次の形式で書きましょう。







ブックメーカーが、イベントaに対する自信の度合いが0.4、つまりP（a） = 0.4であると主張する場合、プレイヤーはブックメーカーの自信の程度に合ったベット額を賭けるかどうかを選択できます。 これは、プレーヤーがブックメーカーの6ルーブルに対して4ルーブルをベットすることで、イベントが発生することに賭けることができることを意味します。 または、プレーヤーは、イベントが起こらないブックメーカーの4ルーブルの代わりに6ルーブルを賭けることができます。



ブックメーカーの信頼度が世界の状態を正確に反映していない場合、長期的には信念がより正確なプレイヤーにお金を失うという事実を当てにすることができます。 さらに、この特定の例では、プレーヤーはブックメーカーが常にお金を失うという戦略を持っています。 それを説明しましょう：







プレーヤーは3回ベットし、チャンピオンシップの結果がどうであれ、常に勝ちます。 優勝賞金の検討には、原則としてウルグアイとドイツのどちらがチャンピオンシップのお気に入りかは含まれません。ブックメーカーの損失は保証されています！ この状況は、ブックメーカーがコルモゴロフの第3公理に違反する確率論の基礎に導かれていないという事実によって導かれました。







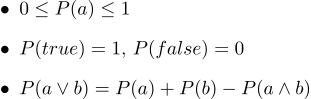
テキスト形式では、次のようになります。

• 1.すべての確率の範囲は0〜1です
• 2.もちろん、真のステートメントの確率は1で、間違いの確率は0です。
• 3. 3番目の公理は分離の公理であり、直観的に理解するのは簡単です。ステートメントaが真である場合と、 bが真である場合は、ステートメントa∨bが真であるすべての場合を確実にカバーします。 ただし、2セットのケースの合計では、それらの交差が2回発生するため、P（a∧b）を減算する必要があります。

1931年、デフィネッティは非常に強力な声明を発表しました。

ブックメーカーが確率論の公理に違反する多くの自信に導かれている場合、各ベットでブックメーカーの損失（プレイヤーの勝利）を保証するようなプレイヤーベットの組み合わせがあります。

確率の公理は、一部のエージェントが保持できる確率的信念のセットを制限するものと見なすことができます。 ブックメーカーのコルモゴロフの公理に従うことは、彼が勝つことを意味するものではないことに注意してください（コミッションの問題は別にしましょう）が、従わない場合、彼は負けることが保証されます。 確率の適用を支持する他の議論が提唱されていることに注意してください。 しかし、確率論に基づいた推論システムの実際的な成功が、多くの見解の修正を引き起こした魅力的なインセンティブであることが判明しました。



それで、Theorverが理にかなっている理由のベールを少し開きましたが、どのようなオブジェクトを操作しますか？ 理論全体は3つの公理のみに基づいています。 3つすべてには、いくつかのマジック関数Pが関係しています。 さらに、これらの公理を見ると、シェイプエリア関数が非常に思い出されます。 面積が確率を決定するように機能するかどうかを確認してみましょう。



「イベント」という言葉を「単位正方形のサブセット」と定義します。 「イベントの確率」という言葉を「対応するサブセットの領域」と定義します。 大まかに言えば、大きな段ボールのターゲットがあり、目を閉じてそれを撃ちます。 特定のセットに弾丸が落ちる可能性は、セットの面積に直接比例します。 この場合の信頼できるイベントは、正方形全体であり、たとえば正方形の任意のポイントなど、明らかに偽です。 確率の定義から、完全にポイントに到達することは不可能であることがわかります（私たちの弾丸は重要なポイントです）。 私は本当に絵が好きで、多くの絵を描きます。理論家も例外ではありません！ 3つの公理すべてを説明しましょう。







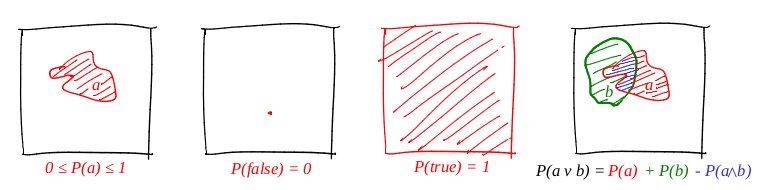
したがって、最初の公理は満たされます。面積は負ではなく、単位を超えることはできません。 信頼できるイベントは正方形全体であり、意図的に誤ったイベントはゼロエリアのセットです。 そして、それは選言と完全に機能します！

例による最大の信頼性

例1：コインフリップ

コイントスの最も単純な例、別名ベルヌーイのスキームを見てみましょう。 N回の実験が行われ、それぞれ2つのイベント（「成功」または「失敗」）が発生する可能性があります。1つは確率pで、もう1つは確率1-pです。 私たちのタスクは、これらのn回の実験で正確にk回成功する確率を見つけることです。 この確率により、ベルヌーイの公式が得られます。







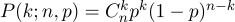
通常のコイン（ p = 0.5 ）を10回投げ（ n = 10 ）、テールが何回落とされるかを考えます：







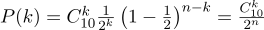
確率密度のグラフは次のとおりです。







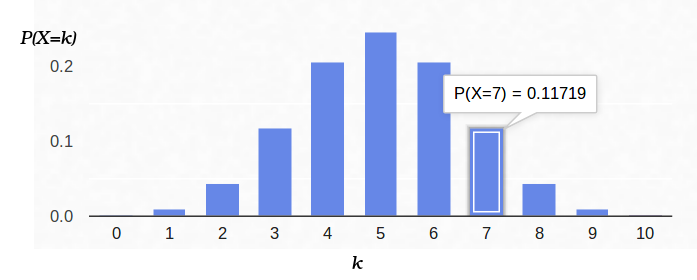
したがって、「成功」の開始の確率（0.5）を修正し、実験の数（10）も修正する場合、「成功」の可能な数は0〜10の任意の整数になりますが、これらの結果は等しくありません。 5つの「成功」を取得することは、1つではないよりもはるかに高い可能性があることは明らかです。 たとえば、7つの頭を数える確率は約12％です。



次に、反対側から同じタスクを見てみましょう。 本当のコインはありますが、先験的な確率「成功」/「失敗」の分布はわかりません。 ただし、10回投げて「成功」の数を数えることができます。 たとえば、7つのテールがあります。 これはどのようにpを評価するのに役立ちますか？



ベルヌーイの公式でn = 10とk = 7を修正し、 pに自由なパラメーターを残してみます。







次に、ベルヌーイの式は、推定されたパラメーターの尤度として解釈できます（この場合はp ）。 関数の文字を変更しましたが、今ではLです （英語のように）。 つまり、尤度は、パラメーターの特定の値に対して観測データ（10回の実験から7回の尾）を生成する確率です。



たとえば、バランスの取れたコイン（ p = 0.5）の可能性は、10トスの7つのテールがドロップされた場合、約12％です。 関数Lをプロットできます：







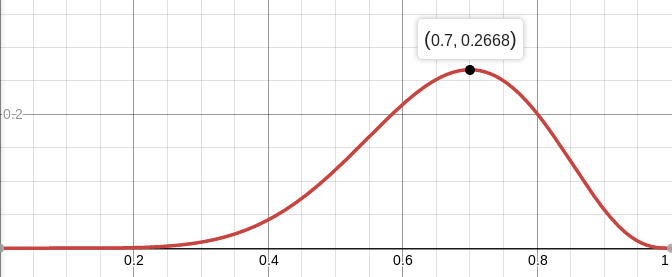
そのため、私たちが持っている観測値を取得する可能性を最大化するパラメーターの値を探しています。 この特定のケースでは、1つの変数の関数があり、その最大値を探しています。 検索を簡単にするために、 Lではなく、 Lの最大値を探します。 対数は厳密に単調な関数であるため、一方と他方を最大化することはまったく同じことです。 そして、対数は製品を区別するのにはるかに便利な量に分割します。 したがって、この関数の最大値を探しています。







これを行うには、その導関数をゼロと同等にします。







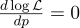
log x = 1 / xの導関数は次のようになります。







つまり、最大尤度（約27％）に到達します。







念のため、2次導関数を計算します。







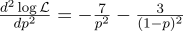
p = 0.7では負であるため、この点は実際にはLの最大値です。







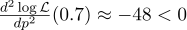
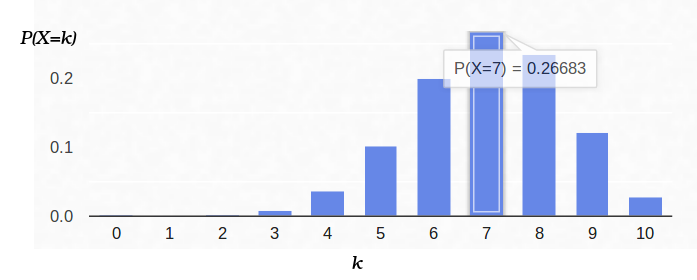
そして、ここにp = 0.7のベルヌーイスキームの確率密度があります：

例2：ADC

測定する特定の一定の物理量があることを想像してみましょう。定規を使った長さでも、電圧計を使った電圧でも。 どんな測定でもこの量の近似値が得られますが、量自体は示されません。 ここで説明する方法は、18世紀の終わりに天体の軌道を測定したガウスによって開発されました。



たとえば、バッテリーの電圧をN回測定すると、N個の異なる測定値が得られます。 どっちがいい？ それだけです！ したがって、N個の数量Ujがあります。







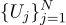
各測定値Ujが理想値とガウスノイズに等しく、ガウスベルの位置とその「幅」という2つのパラメータによって特徴付けられると仮定します。 これは確率密度がどのように見えるかです：







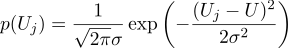
つまり、N個のUjの値を使用して、尤度値を最大化するこのようなパラメーターUを見つけることがタスクです。 信頼性（私はすぐにそれから対数を取ります）は次のように書くことができます：







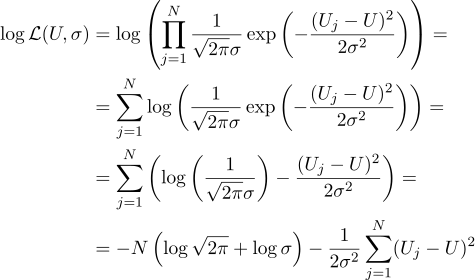
さて、すべてが以前とまったく同じで、探しているパラメーターに関して偏微分をゼロに等しくします：







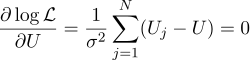
未知の量Uの最も可能性の高い推定値は、すべての測定値の平均として見つけることができます。







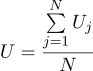
さて、最も可能性の高いシグマパラメーターは通常の標準偏差です。









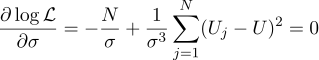
回答のすべての測定値の単純な平均を取得するのは面倒な価値がありましたか？ 私の好みにとって、それは価値がありました。 ところで、測定値の精度を高めるために一定値の複数の測定値を平均化することは標準的な方法です。 たとえば、 ADC平均化 。 ちなみに、このガウスノイズは必要ないので、ノイズがバイアスされていなければ十分です。

例3、そして再び1次元

会話を続けます。同じ例を取り上げますが、少し複雑になります。 特定の抵抗の抵抗値を測定したい。 実験室の電源の助けを借りて、特定の標準数のアンペアを通過させ、これに必要な電圧を測定することができます。 つまり、抵抗エバリュエーターの入力にN組の数値（Ij、Uj）があります。







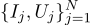
チャートにこれらのポイントを描画します。 オームの法則は、青い線の勾配を探していることを示しています。







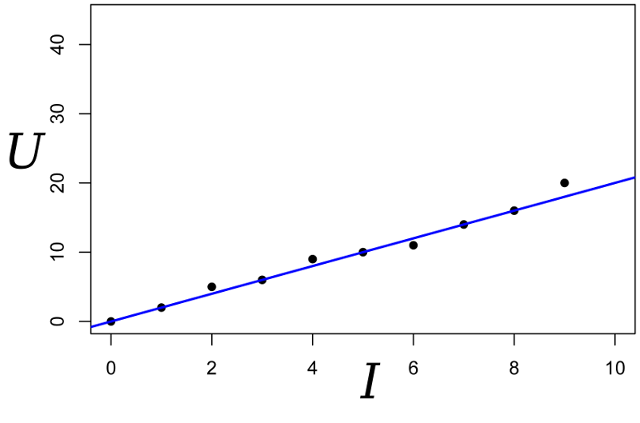
パラメーターRの尤度の式を記述します。







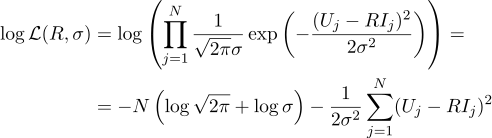
また、対応する偏導関数をゼロに等しくします。







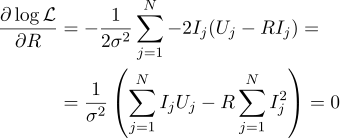
次に、もっともらしい抵抗Rは次の式で求められます。







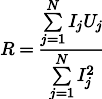
この結果は、すでにすべての測定値の単純な平均よりもやや不明瞭です。 1アンペアの領域で100回の測定を行い、1キロアンペアの領域で1回の測定を行った場合、以前の100回の測定は実際には結果に影響しないことに注意してください。 この事実を思い出しましょう。次の記事で役立つでしょう。

4番目の例：最小二乗に戻る

確かに、最後の2つの例では、尤度対数を最大化することは、推定誤差の二乗和を最小化することと同じであることにすでに気付いています。 別の例を見てみましょう。 基準重量を使用してスチールヤードのキャリブレーションを行います。 質量xjのN個の参照荷重があり、それらをスチールヤードに掛けて、スプリングの長さを測定すると、N個のスプリング長yjが得られます。







フックの法則によれば、バネの伸びは加えられた力に直線的に依存し、この力には商品の重量とバネ自体の重量が含まれます。 バネの剛性をパラメータaとしますが 、自重でのバネの張力はbパラメータです。 次に、この方法で測定の尤度の式を記述できます（以前と同様、ガウス測定ノイズの仮説の下で）。







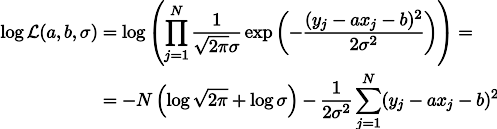
Lの尤度最大化は、推定誤差の二乗和を最小化することと同等です。つまり、次のように定義される関数Sの最小値を探すことができます。







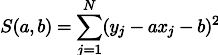
言い換えると、緑のセグメントの長さの平方和を最小化する直線を探しています。







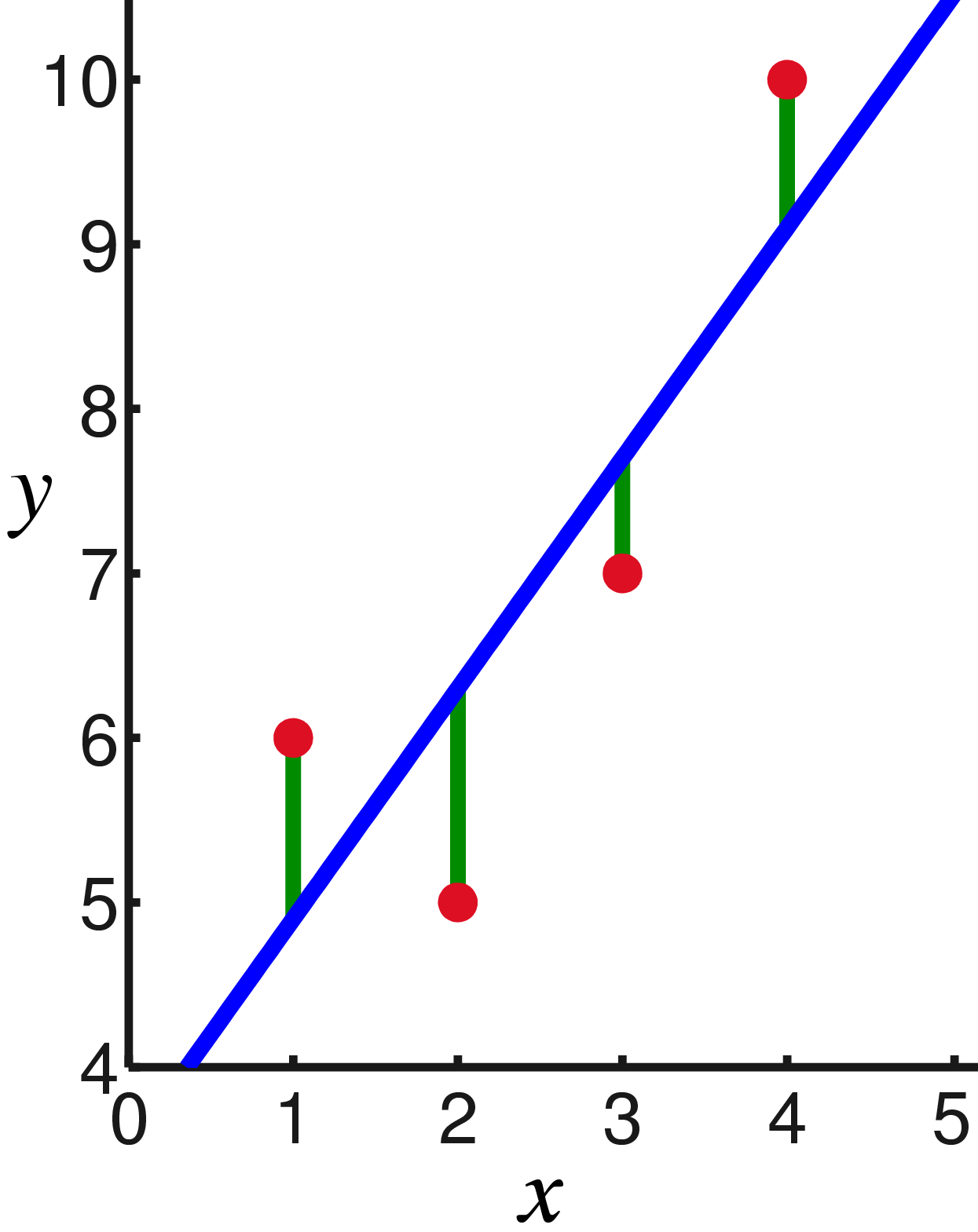
さて、驚くことではありませんが、偏導関数をゼロとみなします。







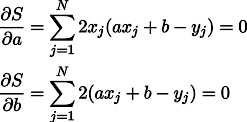
2つの未知数を持つ2つの線形方程式のシステムを取得します。







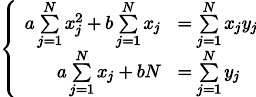
学校の7年生を思い出し、解決策を書きます。

おわりに

最小二乗法は、確率密度がガウスである場合の尤度を最大化する特別な場合です。 密度が（まったくではない）ガウスの場合、最小二乗は最大尤度推定（MLE）とは異なる推定を与えます。 ちなみに、ガウスはかつて、分布は役割を果たさず、テストの独立性のみが重要であると仮定していました。



この記事からわかるように、森の奥に行くほど、この問題に対するより厄介な分析ソリューションになります。 ええ、そうです、18世紀ではありません。コンピューターがあります。 次回は、OLSの問題に対する幾何学的アプローチとプログラムアプローチを見ていきます。