ピクセルを操作する例を使用したk-means（k-means）アルゴリズムの実装

みなさんこんにちは！ 最近、k-meansメソッド（英語のk-means）を使用して画像セグメンテーションを実装するコードを記述する必要がありました。 さて、Googleが最初にすることはヘルプです。 数学的な観点（そこにあるすべての種類の複雑な数学的な落書き、そこに地獄が書かれていることを理解するでしょう）、および英語のインターネット上のいくつかのソフトウェア実装の両方から多くの情報を見つけました。 これらのコードは確かに美しい-疑いの余地はありませんが、アイデアの本質を把握するのは困難です。 どういうわけか、そこはすべて複雑で、混乱していますが、手で、手で、コードを書かず、何も理解できません。 この記事では、単純で生産的ではないが、この素晴らしいアルゴリズムの理解可能な実装を示したいと思います。 さあ、行こう！



それでは、認識の観点からクラスタリングとは何ですか？ 例を挙げましょう。おばあさんのコテージの花の素敵な写真があるとしましょう。







問題は、この写真のほぼ同じ色で塗りつぶされている領域の数を判断することです。 まあ、それはまったく難しくありません：白い花びら-1つ、黄色のセンター-2つ（私は生物学者ではありません、私はそれらが何と呼ばれるかわかりません）、3つの緑。 これらのセクションはクラスターと呼ばれます。 クラスターは、共通の特徴（色、位置など）を持つデータの組み合わせです。 このようなクラスター-セクション内のデータの各コンポーネントを決定して配置するプロセスは、クラスタリングと呼ばれます。



多くのクラスタリングアルゴリズムがありますが、最も単純なものはk-中程度のもので、これについては後で説明します。 K-meansは、ソフトウェアメソッドを使用して簡単に実装できるシンプルで効率的なアルゴリズムです。 クラスタに分散するデータはピクセルです。 ご存じのとおり、カラーピクセルには3つのコンポーネント（赤、緑、青）があります。 これらのコンポーネントの面付けにより、既存の色のパレットが作成されます。







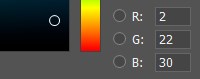
コンピュータのメモリでは、各色成分は0〜255の数字で特徴付けられます。つまり、赤、緑、青の異なる値を組み合わせて、画面上にカラーパレットを取得します。



例としてピクセルを使用して、アルゴリズムを実装します。 K-meansは反復アルゴリズムです。つまり、いくつかの数学的計算を一定回数繰り返した後、正しい結果が得られます。

アルゴリズム

1. データを配信するために必要なクラスターの数を事前に知る必要があります。 これはこの方法の重大な欠点ですが、この問題はアルゴリズムの改善された実装によって解決されますが、これは彼らが言うように、まったく異なる話です。
2. クラスターの初期中心を選択する必要があります。 どうやって？ はい、ランダムに。 なんで？ 各ピクセルをクラスターの中心にスナップできるようにします。 中心は王のようなもので、その周りに彼の主題が集まっています-ピクセル。 各ピクセルが誰に従うかを決定するのは、中心からピクセルまでの「距離」です。
3. 各中心から各ピクセルまでの距離を計算します。 この距離は、空間内のポイント間のユークリッド距離と見なされ、この場合、3つの色成分間の距離と見なされます。

   $$ $$表示$$ \ sqrt {（R_ {2} -R_ {1}）^ 2 +（G_ {2} -G_ {1}）^ 2 +（B_ {2} -B_ {1}）^ 2} 。$$表示$$

   
   
   
   
   最初のピクセルから各中心までの距離を計算し、このピクセルと中心の間の最小距離を決定します。 中心である最小距離は、ピクセルの各コンポーネント-キングとピクセル-被写体の間の算術平均として座標を再計算します。 私たちのセンターは、計算に従って空間をシフトします。
4. すべての中心を再計算した後、ピクセルをクラスターに分配し、各ピクセルから中心までの距離を比較します。 ピクセルはクラスターに配置され、その中心は他の中心よりも近くにあります。
5. ピクセルが同じクラスター内にある限り、すべてが最初から始まります。 大量のデータでは中心が小さな半径で移動し、クラスターの端に沿ったピクセルが一方または他方のクラスターにジャンプするため、これは頻繁に発生しません。 これを行うには、反復の最大数を決定します。

実装

このプロジェクトをC ++で実装します。 最初のファイルは「k_means.h」です。その中で、主なデータ型、定数、および作業用のメインクラス「K_means」を定義しました。

各ピクセルを特徴付けるには、3つのピクセルコンポーネントで構成される構造を作成します。より正確な計算のためにdoubleタイプを選択し、プログラムの定数を決定しました。

const int KK = 10; //  const int max_iterations = 100; //   typedef struct { double r; double g; double b; } rgb;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

K_meansクラス自体：

 class K_means { private: std::vector<rgb> pixcel; int q_klaster; int k_pixcel; std::vector<rgb> centr; void identify_centers(); inline double compute(rgb k1, rgb k2) { return sqrt(pow((k1.r - k2.r),2) + pow((k1.g - k2.g), 2) + pow((k1.b - k2.b), 2)); } inline double compute_s(double a, double b) { return (a + b) / 2; }; public: K_means() : q_klaster(0), k_pixcel(0) {}; K_means(int n, rgb *mas, int n_klaster); K_means(int n_klaster, std::istream & os); void clustering(std::ostream & os); void print()const; ~K_means(); friend std::ostream & operator<<(std::ostream & os, const K_means & k); };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

クラスのコンポーネントを調べてみましょう。



vectorpixcel-ピクセルのベクトル。

q_klaster-クラスターの数。

k_pixcel-ピクセル数。

vectorcentr-クラスタリング中心のベクトル。その中の要素の数はq_klasterによって決定されます。

identity_centers（）-入力ピクセル間で初期中心をランダムに選択する方法。

compute（）およびcompute_s（）は、それぞれピクセル間の距離を計算し、中心を再計算するための組み込みメソッドです。

3つのコンストラクター：最初はデフォルトで、2番目は配列からピクセルを初期化するため、3番目はテキストファイルからピクセルを初期化するためです（私の実装では、ファイルが最初に誤ってデータで満たされ、次にこのファイルからピクセルが読み込まれます。ちょうど私の場合に必要な）;

クラスタリング（std :: ostream＆os）-クラスタリング方法;

メソッドを作成し、出力ステートメントをオーバーロードして結果を公開します。



メソッドの実装：

 void K_means::identify_centers() { srand((unsigned)time(NULL)); rgb temp; rgb *mas = new rgb[q_klaster]; for (int i = 0; i < q_klaster; i++) { temp = pixcel[0 + rand() % k_pixcel]; for (int j = i; j < q_klaster; j++) { if (temp.r != mas[j].r && temp.g != mas[j].g && temp.b != mas[j].b) { mas[j] = temp; } else { i--; break; } } } for (int i = 0; i < q_klaster; i++) { centr.push_back(mas[i]); } delete []mas; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これは、初期クラスタリング中心を選択して中心ベクトルに追加する方法です。 これらの場合、センターを繰り返して交換するためにチェックが実行されます。

 K_means::K_means(int n, rgb * mas, int n_klaster) { for (int i = 0; i < n; i++) { pixcel.push_back(*(mas + i)); } q_klaster = n_klaster; k_pixcel = n; identify_centers(); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

配列からピクセルを初期化するためのコンストラクター実装。

 K_means::K_means(int n_klaster, std::istream & os) : q_klaster(n_klaster) { rgb temp; while (os >> temp.r && os >> temp.g && os >> temp.b) { pixcel.push_back(temp); } k_pixcel = pixcel.size(); identify_centers(); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ファイルとコンソールの両方からデータを入力できるように、このコンストラクターに入力オブジェクトを渡します。

 void K_means::clustering(std::ostream & os) { os << "\n\n :" << std::endl; /*             :        ,    -  ,    ,   ,        .*/ std::vector<int> check_1(k_pixcel, -1); std::vector<int> check_2(k_pixcel, -2); int iter = 0; /* .*/ while(true) { os << "\n\n----------------  №" << iter << " ----------------\n\n"; { for (int j = 0; j < k_pixcel; j++) { double *mas = new double[q_klaster]; /*  :          .      ,   .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[j], centr[i]); os << "   " << j << "   #" << i << ": " << *(mas + i) << std::endl; } /*     m_k      .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } os << "    #" << m_k << std::endl; os << "  #" << m_k << ": "; centr[m_k].r = compute_s(pixcel[j].r, centr[m_k].r); centr[m_k].g = compute_s(pixcel[j].g, centr[m_k].g); centr[m_k].b = compute_s(pixcel[j].b, centr[m_k].b); os << centr[m_k].r << " " << centr[m_k].g << " " << centr[m_k].b << std::endl; delete[] mas; } /*   .*/ int *mass = new int[k_pixcel]; os << "\n  : "<< std::endl; for (int k = 0; k < k_pixcel; k++) { double *mas = new double[q_klaster]; /*    .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[k], centr[i]); os << "   №" << k << "   #" << i << ": " << *(mas + i) << std::endl; } /*  .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } mass[k] = m_k; os << " №" << k << "     #" << m_k << std::endl; } /*            .*/ os << "\n    : \n"; for (int i = 0; i < k_pixcel; i++) { os << mass[i] << " "; check_1[i] = *(mass + i); } os << std::endl << std::endl; os << " : " << std::endl; int itr = KK + 1; for (int i = 0; i < q_klaster; i++) { os << " #" << i << std::endl; for (int j = 0; j < k_pixcel; j++) { if (mass[j] == i) { os << pixcel[j].r << " " << pixcel[j].g << " " << pixcel[j].b << std::endl; mass[j] = ++itr; } } } delete[] mass; /*    .*/ os << " : \n" ; for (int i = 0; i < q_klaster; i++) { os << centr[i].r << " " << centr[i].g << " " << centr[i].b << " - #" << i << std::endl; } } /*         –  .*/ iter++; if (check_1 == check_2 || iter >= max_iterations) { break; } check_2 = check_1; } os << "\n\n ." << std::endl; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

クラスタリングの主な方法。

 std::ostream & operator<<(std::ostream & os, const K_means & k) { os << " : " << std::endl; for (int i = 0; i < k.k_pixcel; i++) { os << k.pixcel[i].r << " " << k.pixcel[i].g << " " << k.pixcel[i].b << " - №" << i << std::endl; } os << std::endl << "   : " << std::endl; for (int i = 0; i < k.q_klaster; i++) { os << k.centr[i].r << " " << k.centr[i].g << " " << k.centr[i].b << " - #" << i << std::endl; } os << "\n : " << k.q_klaster << std::endl; os << " : " << k.k_pixcel << std::endl; return os; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

初期データの出力。

出力例

この例は前もって計画されており、ピクセルはデモ用に選択されています。 プログラムがデータを3つのクラスターにグループ化するには、2回の反復で十分です。 最後の2回の繰り返しの中心を見ると、それらが実際に所定の位置に残っていることがわかります。



さらに興味深いのは、ランダムに生成されたピクセルの場合です。 10個のクラスターに分割する必要がある50個のポイントを生成したので、5回繰り返しました。 3つのクラスターに分割する必要のある50個のポイントを生成したので、最大100回の反復が許可されました。 クラスターが多いほど、プログラムが最も類似したピクセルを見つけてそれらをより小さなグループにまとめるのが簡単になり、逆も同様です-クラスターが少なく、ポイントが多い場合、アルゴリズムは多くの場合、最大反復数を超えたときにのみ終了しますあるクラスターから別のクラスターへ。 ただし、バルクはクラスター内で完全に決定されます。



それでは、クラスタリングの結果を確認しましょう。 10個のクラスターあたり50ポイントの例からいくつかのクラスターの結果を取得し、これらのデータの結果をIllustratorに送り込みました。







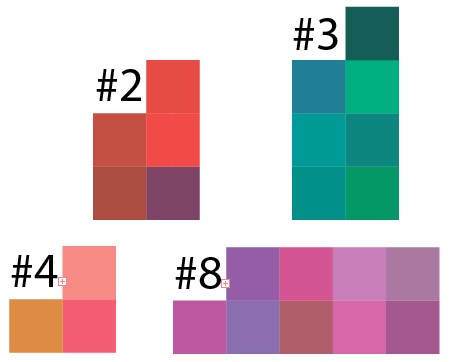
各クラスターでは色の濃淡が優勢であることがわかります。ここでは、ピクセルがランダムに選択されたことを理解する必要があります。実際の生活でのそのような画像の類似物は、すべての色が誤って吹き付けられた何らかの種類の画像であり、同様の色の領域を選択することは困難です



このような写真があるとしましょう。 島を1つのクラスターとして定義することもできますが、増加すると、さまざまな緑の陰影で構成されることがわかります。







これはクラスター8ですが、小さいバージョンでは結果は同様です：







プログラムのフルバージョンは、私のGitHubで表示できます。