多項式時間でのベルトウェイ問題の可解性について

学生は、特にバイオインフォマティクスコースを受講することにより、環状道路の問題を知ることができます。特に、プログラマーにとって最高の品質と精神に最も近いものの1つは、カリフォルニア大学サンディエゴ校のコースラのバイオインフォマティクス（Pavel Pevzner）コースです。 この問題は、ステートメントの単純さ、実際的な重要性、および単純なコーディングでそれを解決する明らかな能力ではまだ解決されていないと考えられるという事実によって注目を集めています。 この方法で問題が提起されます。 多項式時間で点のセットの座標を復元することは可能ですか？ $$ $インライン$ X $インライン$ それらの間のすべてのペアワイズ距離のセットがわかっている場合 $$ $インライン$ \デルタX $インライン$ ？



この一見単純なタスクは、まだ計算幾何学の未解決問題のリストにあります。 さらに、状況は多次元空間のポイント、特に曲線のポイントにも関係しません。すべてのポイントが整数座標を持ち、同じラインにローカライズされる場合、問題はすでに最も簡単なオプションです。



このタスクが数学者によって課題として認識されてからほぼ半世紀（Shamos、1975）で、いくつかの結果が得られました。 1次元の問題に対して2つのケースが考えられます。

1. ポイントは直線上にあります（ターンパイクの問題）
2. ポイントは円上にあります（ベルトウェイの問題）

これらの2つのケースは、理由のために異なる名前を受け取りました-それらを解決するのに異なる努力が必要です。 実際、最初の問題は十分に迅速に（15年で）解決され、バックトラッキングアルゴリズムが構築されました。これにより、平均で2次時間で解が復元されます。 $$ $インライン$ O（n ^ 2 \ log n）$インライン$ どこで $$ $インライン$ n $インライン$ -ポイント数（Skiena、1990）; 2番目のタスクの場合、これはこれまで行われておらず、提案された最適なアルゴリズムは指数関数的な計算の複雑さを持っています $$ $インライン$ O（n ^ n \ log n）$インライン$ （Lemke、2003）。 下の画像は、異なるポイント数のセットの解を得るためにコンピューターがどれくらいの時間動作するかを示しています。







つまり、心理的に許容できる時間（10秒以内）で、多くの $$ $インライン$ X $インライン$ ターンパイクケースでは最大1万ポイント、ベルトウェイケースでは最大10ポイントです。これは実際の用途にはまったく価値がありません。



少し説明。 ターンパイクの問題は、実用的な観点から、つまり遭遇するデータの大部分について解決されると考えられています。 この場合、解を得るための時間が指数関数的に無視される特別なデータセットがあるという事実に対する純粋な数学者の反対 $$ $インライン$ O（2 ^ n \ log n）$インライン$ （チャン、1982）。 ターンパイクとは対照的に、指数アルゴリズムのベルトウェイ問題は、何らかの方法で解決されたとは見なされません。

バイオインフォマティクスの観点から環状道路問題を解決することの重要性

20世紀の終わりに、非リボソーム合成経路と呼ばれる生体分子合成の新しい経路が発見されました。 従来の合成ルートとの主な違いは、最終的な合成結果がDNAにまったくエンコードされていないことです。 代わりに、これらのオブジェクトを収集できる「ツール」（多くの異なるシンセターゼ）のコードのみがDNAに書き込まれます。 したがって、バイオマシンエンジニアリングは大幅に強化されており、わずか20種類の標準部品（タンパク質構成とも呼ばれる標準アミノ酸）で動作する単一タイプのコレクター（リボソーム）の代わりに、500を超える標準部品および非標準部品で動作できる他の多くのタイプのコレクターが登場します（非タンパク質構成アミノ酸とそのさまざまな修飾）。 また、これらのアセンブラは、パーツをチェーンに接続するだけでなく、非常に複雑な構造（周期的、分岐、および多くのサイクルと分岐を持つ構造）を取得できます。 これはすべて、その生活のさまざまなケースで細胞の兵器庫を大幅に増加させます。 そのような構造の生物学的活性は高く、特異性（作用の選択性）もさまざまな特性-制限されていません。 英語の文献におけるこれらの細胞産物のクラスは、NRP（非リボソーム産物、または非リボソームペプチド）と呼ばれています。 生物学者は、非常に効果的であり、特異性による副作用のない新しい薬理学的製剤を見つけることができるのは、まさにそのような細胞代謝の産物であることを望んでいます。



唯一の質問は、NRPをどのように、どこで探すかです。 それらは非常に効果的であるため、細胞はそれらを大量に生産する必要が全くなく、その濃度は無視できる。 そのため、約1％の低い精度と膨大な試薬と時間コストを伴う化学抽出法は役に立ちません。 次。 これらはDNAにエンコードされていないため、ゲノムのデコード中に蓄積されたすべてのデータベース、およびバイオインフォマティクスとゲノミクスのすべての方法も役に立たないことを意味します。 何かを見つける唯一の方法は、物理的方法、つまり質量分析によるものです。 さらに、現代の分光計での物質の検出レベルは非常に高いため、重要でない量、合計>〜800分子（アトモル範囲、または濃度）を見つけることができます $$ $インライン$ 10 ^ {-18} $インライン$ ）



」



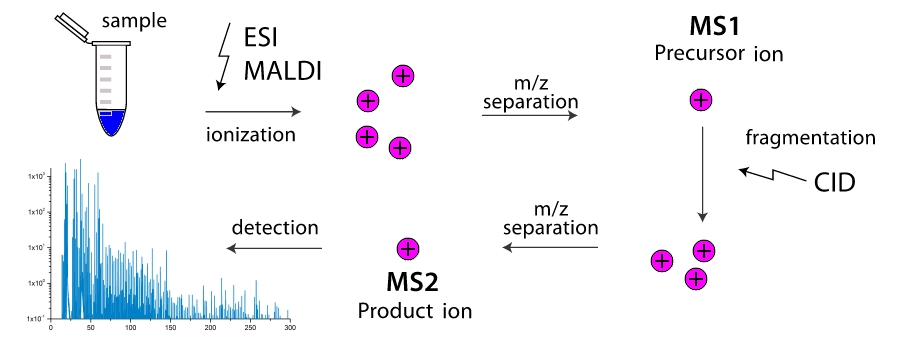質量分析計はどのように機能しますか？ 装置の作業室では、分子は破片に分解されます（外部衝突による頻度は低くなりますが、相互の衝突による頻度が高くなります）。 これらのフラグメントはイオン化され、外部の電磁場で加速および分離されます。 分離は、検出器に到達する時間、または磁場の回転角のいずれかで発生します。これは、フラグメントの質量が大きく、電荷が低いため、不器用になるためです。 したがって、質量分析計は断片の質量を「計量」します。 さらに、「質量」は、同じ質量（より正確には、1つの値 $$ $インライン$ m / z $インライン$ ）さらにフラグメンテーションを進め、さらに分離します。 2段質量分析計は広く分布しており、タンデム質量分析計と呼ばれています。多段質量分析計は非常にまれであり、単に $$ $インライン$ ms ^ n $インライン$ どこで $$ $インライン$ n $インライン$ -ステージの数。 そして、ここで、その構造を知るために、どのようにして、あらゆる分子のあらゆる種類のフラグメントの質量だけを知るというタスクが現れますか？ そこで、それぞれ線形ペプチドと環状ペプチドについて、ターンパイクとベルトウェイの問題になりました。



環状ペプチドの例を使用して、生体分子の構造を復元するタスクが示された問題にどのように軽減されるかについて、さらに詳しく説明します。







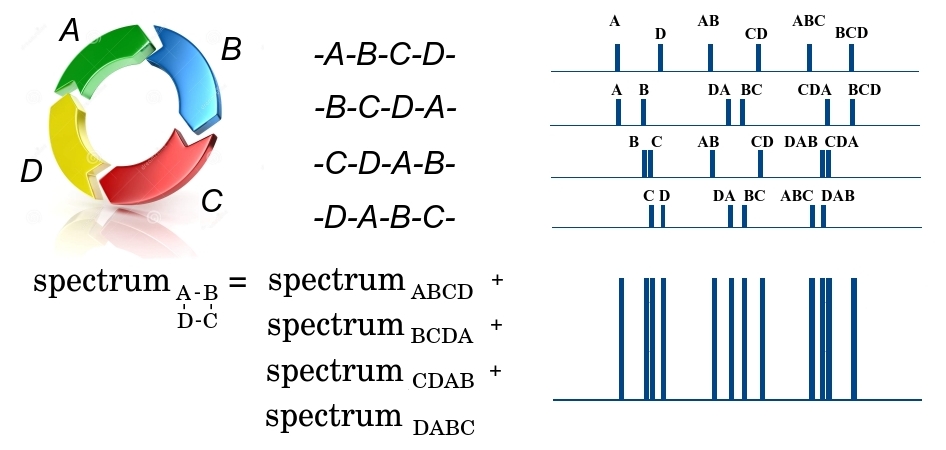
断片化の最初の段階での環状ペプチドABCDは、DA結合またはAB、BCまたはCDのいずれかによって4箇所で切断され、4つの可能な線形ペプチド（ABCD、BCDA、CDABまたはDABC）を形成します。 膨大な数の同一のペプチドが分光計を通過するため、出力には4つのタイプすべてのフラグメントがあります。 さらに、すべてのフラグメントは同じ質量を持ち、最初の段階で分離できないことに注意してください。 2番目の段階では、線形フラグメントABCDを3つの場所で分割し、異なる質量AとBCD、ABとCD、ABCとDの小さなフラグメントを形成し、対応する質量スペクトルを形成します。 このスペクトルでは、フラグメントの質量がx軸に沿って、特定の質量を持つ小さなフラグメントの数がy軸に沿ってプロットされます。 同様に、BCDA、CDAB、DABCの残りの3つの線形フラグメントのスペクトルが形成されます。 4つの大きなフラグメントすべてが第2ステージに渡されるため、それらのすべてのスペクトルが合計されます。 合計、結果はある程度の質量です $$ $ inline $ \ {m_1 ^ {n_1}、m_2 ^ {n_2}、..、m_q ^ {n_q} \} $ inline $ どこで $$ $インライン$ m_i $インライン$ -いくつかの質量、および $$ $インライン$ n_i $インライン$ -その繰り返しの頻度。 ただし、異なる質量が同じ質量を持つ可能性があるため、この質量がどのフラグメントに属し、このフラグメントが一意であるかどうかはわかりません。 ペプチドの結合が互いに離れているほど、ペプチドフラグメントの質量は大きくなります。 つまり、環状ペプチドの要素の順序を復元するタスクは、ベルトウェイの問題になります。 $$ $インライン$ X $インライン$ ペプチドの結合、および多数の要素 $$ $インライン$ \デルタX $インライン$ -結合間のフラグメントの塊。

ベルトウェイ問題を解決するための多項式時間を備えたアルゴリズムの存在の予測

私の経験と、この問題を解決しようとした人や実際に何かをした人とのコミュニケーションから、大多数の人が一般的な場合、またはこのような狭い範囲の整数データのいずれかで解決しようとしていることに気付きました（1、 50）。 どちらのオプションも失敗する運命にあります。 一般的な場合、一次元の場合のベルトウェイ問題の解決策の総数が証明されました。 $$ $インライン$ S_1（n）$インライン$ 値による制限（Lemke、2003）

$$ $$ディスプレイ$$ e ^ {2 ^ {\ frac {\ ln n} {\ ln \ ln n} + o（1）}} \ leq S_1（n）\ leq \ frac {1} {2} n ^ {n-2} $$ディスプレイ$$

これは、漸近線に指数関数的な数の解が存在することを意味します $$ $インライン$ n \右矢印\ infty $インライン$ 。 明らかに、ソリューションの数が指数関数的に増加した場合、それらの受信時間はそれ以上遅くなることはありません。 つまり、一般的な場合、多項式時間解を取得することは不可能です。 狭い範囲の整数データに関しては、すべてを実験的にチェックできます。徹底的な検索によって解決策を探すコードを書くのはそれほど難しくないからです。 小さい方に $$ $インライン$ n $インライン$ このようなコードはそれほど長くかかりません。 そのようなコードのテスト結果は、そのようなデータ条件の下で、任意のセットの異なるソリューションの総数が表示されます $$ $インライン$ \デルタX $インライン$ すでに小さい $$ $インライン$ n $インライン$ また、非常に劇的に成長しています。



これらの事実について学んだ後、あなたは条件に達し、このタスクをあきらめることができます。 これが、ベルトウェイの問題が未解決のままであると考えられる理由の1つであると認めます。 ただし、抜け穴は存在します。 指数関数であることを思い出してください $$ $インライン$ e ^ {\ alpha x} $インライン$ 非常に興味深い動作をします。 最初は、非常にゆっくりと成長し、0から1に無限に大きな間隔で上昇します。 $$ $ inline $ \ infty $ inline $ 0にすると、その成長はますます加速します。 ただし、値が低いほど $$ $インライン$ \ alpha $インライン$ 値が大きいほど $$ $インライン$ x $インライン$ 関数の結果が設定値をステップオーバーするように $$ $インライン$ y = \ xi $インライン$ 。 そのような値として、数字を選択すると便利です $$ $インライン$ \ xi = 2 $インライン$ 、彼の前に唯一の解決策、彼の後に多くの決定があります。 質問 そして、誰がどのデータが入力に到達するかに関する決定の数の依存性をチェックしましたか？ はい、しました。 クロアチアの女性数学者Tamara Dakis（Dakic、2000）による素晴らしいphD論文があり、多項式時間で問題を解決するために入力データが満たすべき条件を決定しました。 最も重要なのは、ソリューションの一意性と入力データのセットに重複がないことです。 $$ $インライン$ \デルタX $インライン$ 。 彼女の博士論文のレベルは非常に高いです。 この学生がターンパイクの問題だけに限定したのは残念ですが、もし彼女が環状道路の問題に関心を向けていたら、それは長い間解決されていたと確信しています。

多項式時間解法ベルトウェイ問題を伴うアルゴリズムの取得

偶然に目的のアルゴリズムを構築できるデータを見つけることができました。 追加のアイデアが必要でした。 主なアイデアは、環状ペプチドのスペクトルは、単一の環切断で形成されるすべての線形ペプチドのスペクトルの合計であるという観察（上記参照）から生まれました。 ペプチド内のアミノ酸配列は、このような線形ペプチドから復元できるため、スペクトル内のラインの総数は重要です（ $$ $インライン$ n $インライン$ 回どこ $$ $インライン$ n $インライン$ -ペプチド内のアミノ酸の数）が過剰です。 問題は、シーケンスを復元する機能を失わないために、どの行をスペクトルから除外するかだけです。 両方のタスク（質量スペクトルからの環状ペプチド配列の復元とベルトウェイの問題）は数学的に同型なので、多くのタスクを間引くことも可能です。 $$ $インライン$ \デルタX $インライン$ 。



間伐作業 $$ $インライン$ \デルタX $インライン$ セットのローカル対称性を使用して構築された $$ $インライン$ \デルタX $インライン$ （Fomin、2016a）。

• 対称化 最初の操作は、セットの任意の要素を選択することです $$ $ inline $ x _ {\ mu} \ in \ Delta X $ inline $ から削除 $$ $インライン$ \デルタX $インライン$ 点に関して対称的なペアを持つ要素を除くすべての要素 $$ $インライン$ x _ {\ mu} / 2 $インライン$ そして $$ $インライン$（L + x _ {\ mu}）/ 2 $インライン$ どこで $$ $インライン$ L $インライン$ -円周（環状道路の場合、すべてのポイントが円上にあることを思い出します）。
• 部分解畳み込み。 2番目の操作では、解に関する推測を使用します。つまり、解に属する個々のポイントの知識、いわゆる部分解を使用します。 多くの $$ $インライン$ \デルタX $インライン$ 条件を満たす要素を除き、すべての要素も削除されます。チェック対象のポイントから部分解のすべてのポイントまでの距離を測定すると、取得されたすべての値は $$ $インライン$ \デルタX $インライン$ 。 取得した距離の少なくとも1つが存在しない場合、 $$ $インライン$ \デルタX $インライン$ その点は無視されます。

定理は、両方の操作がセットを間引くことを証明しました $$ $インライン$ \デルタX $インライン$ 、ただし、ソリューションを復元するのに十分な要素が残っています $$ $インライン$ X $インライン$ 。 これらの操作を使用して、アルゴリズムが構築され、c ++で実装され、ベルトウェイの問題を解決しました（Fomin、2016b）。 このアルゴリズムは、従来のバックトラッキングアルゴリズムとほとんど異なりません（つまり、可能なオプションを列挙して解決策を構築し、構築中にエラーが発生した場合に戻ります）。 唯一の違いは、セットを絞り込むことです $$ $インライン$ \デルタX $インライン$ 私たちをテストするためのオプションはかなり少なくなります。



これがいくつの例です $$ $インライン$ \デルタX $インライン$ 間伐中。







ランダムに生成された長さの環状ペプチドについて計算実験が行われた $$ $インライン$ n $インライン$ 10〜1000個のアミノ酸（対数目盛の縦軸）。 対数目盛の横軸は、さまざまな操作によって間引きされたセット内の要素の数を示します $$ $インライン$ \デルタX $インライン$ 単位で $$ $インライン$ n $インライン$ 。 そのような表現は絶対に珍しいので、例によってどのように読まれるかを解読します。 左の図を見てください。 ペプチドに長さを持たせます $$ $インライン$ n = 100 $インライン$ 。 彼にとって、セット内の要素の数 $$ $インライン$ \デルタX $インライン$ 等しい $$ $インライン$ n ^ 2 = 10000 $インライン$ （これは上の破線の点です $$ $インライン$ y = n ^ 2 $インライン$ ） セットから削除した後 $$ $インライン$ \デルタX $インライン$ 繰り返し要素、要素数 $$ $インライン$ \デルタX $インライン$ に減少 $$ $インライン$ n_D \約n ^ {1.9} \約6300 $インライン$ （十字付きの円）。 対称化の後、要素の数は $$ $インライン$ n_S \約n ^ {1.75} \約3100 $インライン$ （黒丸）、および部分解による畳み込み後 $$ $インライン$ n_C \約n ^ {1.35} \約500 $インライン$ （クロス）。 合計、セットの合計ボリューム $$ $インライン$ \デルタX $インライン$ わずか20倍に削減されました。 同じ長さのペプチドですが、右の図では、収縮は $$ $インライン$ n ^ 2 = 10000 $インライン$ 前に $$ $インライン$ N_C \約n \約100 $インライン$ 、つまり100回。



左図のテストケースの生成は、複製のレベルが $$ $インライン$ k_ {dup} $インライン$ で $$ $インライン$ \デルタX $インライン$ 0.1から0.3の範囲で、右側の場合は0.1未満でした。 複製のレベルは次のように定義されます $$ $ inline $ k_ {dup} = 2- \ log {N_u} / \ log {n} $ inline $ どこで $$ $インライン$ N_u $インライン$ -セット内の一意の要素の数 $$ $インライン$ \デルタX $インライン$ 。 そのような定義は自然な結果をもたらします：セットに重複がない場合 $$ $インライン$ \デルタX $インライン$ その力は $$ $インライン$ N_u = n ^ 2 $インライン$ そして $$ $インライン$ k_ {dup} = 0 $インライン$ 可能な限り最高の複製で $$ $インライン$ N_u = n $インライン$ そして $$ $インライン$ k_ {dup} = 1 $インライン$ 。 異なるレベルの複製を提供できるようにする方法については、少し後で説明します。 図は、複製のレベルが低いほど、間引きされることを示しています $$ $インライン$ \デルタX $インライン$ で $$ $インライン$ k_ {dup} <0.1 $インライン$ 間引きされた要素の数 $$ $インライン$ \デルタX $インライン$ 一般的にその限界に達する $$ $インライン$ O（n ^ 2）\右矢印O（n）$インライン$ 、間引きされたセットでは $$ $インライン$ O（n）$インライン$ 要素を取得できません（操作には、 $$ $インライン$ n $インライン$ 要素）。 セットの力を狭めるという事実 $$ $インライン$ \デルタX $インライン$ 下限値を設定することは非常に重要です。ソリューションを取得する計算の複雑さを劇的に変えるのは彼です。



間引き操作をバックトラッキングアルゴリズムに挿入し、ベルトウェイの問題を解決した後、タマラダキスがターンパイクの問題に関して話したことの完全な類似物が明らかになりました。 思い出させてください。 彼女は、ターンパイク問題では、解が一意であり、重複がない場合、多項式時間で解を得ることができると言いました。 $$ $インライン$ \デルタX $インライン$ 。 重複を完全になくす必要はなく（実際のデータではほとんど不可能です）、そのレベルは非常に小さくなります。 次の図は、ペプチドの長さと複製のレベルに応じて、ベルトウェイの問題の解決に必要な時間を示しています $$ $インライン$ \デルタX $インライン$ 。







図では、横座標と縦座標の両方が対数目盛で示されています。 これにより、カウント時間のシーケンスへの依存性を明確に確認できます $$ $インライン$ T = f（n）$インライン$ 指数関数（直線）または多項式（対数曲線）。 図に見られるように、低レベルの複製（右図）では、解は多項式時間で得られます。 さて、より正確には、解は二次時間で得られます。 これは、間引き操作によってセットのパワーが下限に低下した場合に発生します。 $$ $インライン$ O（n ^ 2）\右矢印O（n）$インライン$ 、残っているポイントはほとんどなく、オプションの繰り返しが単一になると戻り、本質的にアルゴリズムはオプションの繰り返しを停止しますが、残っているものからソリューションを構築します。



PSさて、複製の異なるレベルでのセットの生成に関する最後の秘密を明らかにします。 これは、データ表示の精度が異なるためです。 データが低い精度（整数への丸めなど）で生成された場合、重複のレベルは0.3以上になります。 たとえば、小数点以下3桁までの精度でデータが生成された場合、複製のレベルは急激に低下し、0.1未満になります。 そして、ここから最後の最も重要な発言が続きます。



実際のデータの場合、測定の精度がますます向上する状況では、ベルトウェイの問題はリアルタイムで解決可能になります。





文学



1. Dakic、T.（2000）。 ターンパイク問題について。 博士論文、サイモンフレイザー大学。

2.フォミン。 E.（2016a）シーケンス問題のn ^ 2ステップのn ^ 2ペアワイズ距離のマルチセットからのポイントセットの再構築への簡単なアプローチ：I.理論。 J Comput Biol。 2016、23（9）：769-75。

3.フォミン。 E.（2016b）シーケンス問題のn ^ 2ステップにおけるn ^ 2ペアワイズ距離のマルチセットからのポイントセットの再構築への簡単なアプローチ：II。 アルゴリズム。 J Comput Biol。 2016、23（12）：934-942。

4. Lemke、P.、Skiena、S.、およびSmith、W.（2003）。 点間距離からセットを再構築します。 離散および計算幾何学アルゴリズムと組み合わせ論、25：597–631。

5. Skiena、S.、Smith、W。、およびLemke、P.（1990）。 点間距離からセットを再構築します。 計算幾何学に関する第6回ACMシンポジウムの議事録、332〜339ページ。 カリフォルニア州バークレー

6. Zhang、Z.1982。部分ダイジェストマッピングアルゴリズムの指数関数的な例。 J. Comp。 バイオ 1、235〜240。