abc仮説の数値検証（はい、その1つ）

こんにちは、Habr。



Geektimes Habrでのabc仮説に関する記事が既にいくつかあります（たとえば、 2013年と2018年 ）。 最初は長年証明できず、その後同じ年数を検証できない定理についての物語自体は、少なくとも長編映画に値することは確かです。 しかし、この素晴らしい物語の陰で、定理自体はあまりにも面白すぎると考えられていますが、それほど面白くはありません。 少なくとも、abc仮説が現代科学の数少ない未解決の問題の1つであるという事実は、5年生でも理解できる問題の声明です。 この仮説が本当に正しい場合、他の重要な定理の証明、たとえばフェルマーの定理の証明に簡単に従う。



Motizukiの栄誉を主張することなく、仮説で約束された平等がどれだけ満たされているかをコンピューターで確認することにしました。 実際、そうではない-現代のプロセッサはゲームをプレイするだけではありません-その主な（計算）目的でコンピューターを使用しないのはなぜですか...



猫の下で、誰が何が起こったか気にしてください。

問題の声明

最初から始めましょう。 定理とは何ですか？ ウィキペディアが言うように（英語版の表現はもう少し明確です）、相互に単純な（共通の除数がない）a、b、cの場合、a + b = c、ε> 0の場合、トリプルa + bの数は限られています = c、そのような：







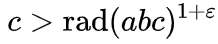
rad関数はradicalと呼ばれ、数の素因数の積を示します。 たとえば、rad（16）= rad（2 * 2 * 2 * 2）= 2、rad（17）= 17（17は素数）、rad（18）= rad（2 * 3 * 3）= 2 * 3 = 6、rad（1,000,000）= rad（2 ^ 6⋅5 ^ 6）= 2 * 5 = 10。



実際、定理の本質は、そのようなトリプルの数が非常に少ないことです。 たとえば、ε= 0.2および等式100 + 27 = 127をランダムに取る場合、rad（100）= rad（2 * 2 * 5 * 5）= 10、rad（27）= rad（3 * 3 * 3）= 3 rad（127）= 127、rad（a * b * c）= rad（a）* rad（b）* rad（c）= 3810、3810 ^ 1.2は明らかに127より大きく、不等式は成り立ちません。 ただし、例外はあります。たとえば、49 + 576 = 625の等式の場合、定理の条件は満たされます（希望する人は自分で確認できます）。



定理によれば、次の重要な瞬間はこれらの平等の限られた数です。 つまり これは、単にコンピューター上でそれらをすべて整理しようとすることができることを意味しています。 その結果、これはノーベル賞に非常に興味深いプログラミング作業を与えます。



それでは始めましょう。

ソースコード

最初のバージョンはPythonで書かれており、この言語はこのような計算には遅すぎますが、コードを記述するのは簡単でシンプルで、プロトタイピングには便利です。



ラジカルを取得する ：数を素因数に分解してから、繰り返しを削除し、配列をセットに変換します。 次に、すべての要素の積を取得します。

def prime_factors(n): factors = [] # Print the number of two's that divide n while n % 2 == 0: factors.append(int(2)) n = n / 2 # n must be odd at this point so a skip of 2 ( i = i + 2) can be used for i in range(3, int(math.sqrt(n)) + 1, 2): # while i divides n , print i ad divide n while n % i == 0: factors.append(int(i)) n = n / i # Condition if n is a prime number greater than 2 if n > 2: factors.append(int(n)) return set(factors) def rad(n): result = 1 for num in prime_factors(n): result *= num return result
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

相互に素数 ： 数を因数分解し 、集合の共通部分をチェックします。

 def not_mutual_primes(a,b,c): fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c) return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

チェック ：既に作成された関数を使用します。ここではすべてが簡単です。

 def check(a,b,c): S = 1.2 # Eps=0.2 if c > (rad(a)*rad(b)*rad(c))**S and not_mutual_primes(a, b, c): print("{} + {} = {} - PASSED".format(a, b, c)) else: print("{} + {} = {} - FAILED".format(a, b, c)) check(10, 17, 27) check(49, 576, 625)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

希望する人は、上記のコードを任意のオンラインPython言語エディターにコピーして、自分で実験することができます。 もちろん、コードは期待どおりに実行され、すべてのトリプルを少なくとも100万個まで列挙するのは長すぎます。 ネタバレの下に最適化されたバージョンがあり、それを使用することをお勧めします。



最終バージョンは、マルチスレッドといくつかの最適化を使用してC ++で書き直されました（交差セットを使用したCでの作業はハードコアですが、おそらく高速になります）。 ソースコードはスポイラーの下にあり、無料のg ++​​コンパイラでコンパイルできます。コードはWindows、OSX、さらにはRaspberry Piでも動作します。





C ++コンパイラをインストールするのが面倒な人のために、少し最適化されたPythonバージョンが提供されており、任意のオンラインエディタで実行できます（ https://repl.it/languages/pythonを使用しました）。

結果

トリプルa、b、cは実際にはごくわずかです。



以下にいくつかの結果を示します。

N = 10 ：1「3」、リードタイム<0.001c

1 + 8 = 9



N = 100 ：2“トリプル”、ランタイム<0.001c

1 + 8 = 9

1 + 80 = 81



N = 1000 ：8「トリプル」、ランタイム<0.01c

1 + 8 = 9

1 + 80 = 81

1 + 242 = 243

1 + 288 = 289

1 + 512 = 513

3 + 125 = 128

13 + 243 = 256

49 + 576 = 625



N = 10000 ：23「トリプル」、ランタイム2秒





N = 100000 ：53「トリプル」、ランタイム50c





N = 1,000,000の場合、 102個の「トリプル」しかなく、完全なリストがネタバレの下に表示されます。





残念ながら、プログラムはまだゆっくりと動作し、N = 10,000,000の結果を待たず、計算時間は1時間以上です（どこかでアルゴリズムの最適化を間違えた可能性があります。



さらに興味深いのは、結果をグラフィカルに見ることです。







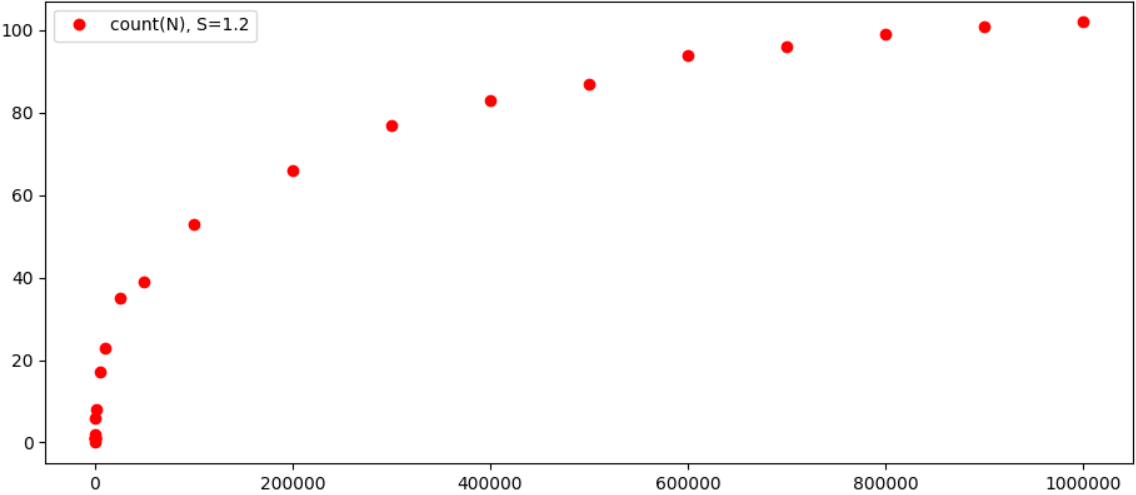
原則として、可能なトリプルの数のNへの依存性がN自体よりも著しく遅くなることは非常に明白であり、結果は各εの特定の数に収束する可能性があります。 ところで、εが増加すると、トリプルの数が著しく減少します。たとえば、ε= 0.4の場合、N <100000（1 + 4374 = 4375および343 + 59049 = 59392）に対して2つの等式しかありません。 そのため、一般に、定理は本当に成り立っているようです（まあ、おそらく、より強力なコンピューターで既にテストされており、おそらくこれはすべて長い間計算されています）。



希望する人は自分で実験することができます。誰かが10,000,000以上の数字の結果を持っているなら、私は喜んでそれらを記事に加えます。 もちろん、「トリプル」のセットが完全に成長を停止する瞬間まで「カウント」することは興味深いでしょうが、非常に長い時間がかかる可能性があり、計算速度はNにN * N（またはN ^ 3）とても長い。 それにもかかわらず、驚くべきものが近くにあり、希望する人は検索に参加することができます。



編集：コメントで示唆されているように、ウィキペディアには結果の表がすでにあります-Nから10 ^ 18の範囲で「トリプル」の数はまだ増え続けているため、セットの「終わり」はまだ見つかりません。 さらに興味深いことに、陰謀は依然として保存されています。