翻訳者から：正確に175年と3日前に四元数が発明されました。 このラウンドの日付に敬意を表して、私はこの概念を明確な言語で説明する資料を取り上げることにしました。



四元数の概念は、アイルランドの数学者ウィリアムローワンハミルトンirによって、1843年10月16日月曜日にアイルランドのダブリンで発明されました。 ハミルトンと彼の妻はロイヤルアイルランドアカデミーに行き、ブルームブリッジを越えてロイヤル運河を渡りました 。彼は驚くべき発見をし、すぐに橋の石をひっかきました。

$$

$$i ^ 2 = j ^ 2 = k ^ 2 = ijk = -1$$

四元数の乗算の基本式が発見されたことに敬意を表して、王立運河に架かるブルーム橋の記念額。



この記事では、四元数の概念をわかりやすい方法で説明しようとします。 クォータニオンを視覚化する方法を説明し、クォータニオンで実行できるさまざまな操作についても説明します。 さらに、マトリックス、オイラー角および四元数の使用を比較し、オイラー角またはマトリックスの代わりに四元数を使用する場合と、不要な場合の説明を試みます。

内容

• 1.はじめに
• 2.複素数
  • 2.1。 複素数の加算と減算
  • 2.2。 複素数とスカラー値の乗算
  • 2.3。 複素数の積
  • 2.4。 複素数の二乗
  • 2.5。 共役複素数
  • 2.6。 複素数の絶対値
  • 2.7。 2つの複素数の商
• 3.度 $$$i$
• 4.複雑な飛行機
  
  
  • 4.1。 ローター
• 5.四元数
  • 5.1。 順序ペアとしての四元数
  • 5.2。 四元数の加算と減算
  • 5.3。 四元数積
  • 5.4。 リアルクォータニオン
  • 5.5。 スカラー四元数乗算
  • 5.6。 純粋な四元数
  • 5.7。 加算四元数形式
  • 5.8。 単一四元数
  • 5.9。 四元数バイナリ形式
  • 5.10。 共役四元数
  • 5.11。 四元数ノルム
  • 5.12。 四元数の正規化
  • 5.13。 逆四元数
  • 5.14。 クォータニオンスカラープロダクト
• 6.ターン
• 7.クォータニオンの補間
  
  
  • 7.1。 SLERP
    
    
    • 7.1.1。 四元数の差
    • 7.1.2。 四元数を累乗する
    • 7.1.3。 四元数の分数差
    • 7.1.4。 考慮すべき要素
  • 7.2。 分隊
• 8.結論
• 9.デモをダウンロードする
• 10.参照

45分でクォータニオンを完全に理解することはできません。



この記事には多くの数学が含まれているため、弱虫向けではありません。

はじめに

コンピュータグラフィックスでは、空間内の位置（変位）と空間内の方向（回転）を記述するためにマトリックスが使用されます。 単一の変換マトリックスを使用して、オブジェクトのスケールを記述することもできます。 この行列は「基底空間」と見なすことができます。 ベクトルまたはポイント（または別のマトリックス）に変換のマトリックスを掛けると、このベクトル、ポイント、またはマトリックスをこのマトリックスで表される空間に「変換」します。



この記事では、変換マトリックスについて詳しく説明しません。 私のマトリックスの記事で変換マトリックスの詳細を読むことができます。



この記事では、クォータニオンを使用して空間内のオブジェクトの方向（回転）を記述する別の方法について説明します。

複素数

クォータニオンを完全に理解するためには、まずクォータニオンがどこから来たのかを理解する必要があります。 四元数の原理は、複素数システムの概念に基づいています。



既知の数値セット（ natural 、 integer 、 realおよびrational ）に加えて、複素数のシステムは虚数と呼ばれる新しい数値セットを追加します。 架空の数値は、解のない特定の方程式を解くために考案されました。たとえば：

$$

$$x ^ 2 + 1 = 0$$

この式を解決するには、 $$$x ^ 2 = -1$ 、そして、ご存知のように、これは不可能です。なぜなら、任意の数の二乗（正または負）は常に正だからです。



数学者は、式に解がないことを受け入れられなかったため、新しい概念が発明されました。そのような方程式を解くために使用できる虚数です。



虚数は次のとおりです。

$$

$$i ^ 2 = -1$$

この仮定を理解しようとしないでください。なぜなら、その存在には論理的な理由がないからです。 それを受け入れるだけです $$$i$ -正方形は $$$-1$ 。



虚数のセットは次のように表すことができます $$$\ mathbb {I}$ 。



複素数のセット（で示される $$$\ mathbb {C}$ 次の形式の実数と虚数の合計です。

$$

$$z = a + bi ~~ a、b \ in \ mathbb {R}、~~ i ^ 2 = -1$$

また、すべての実数は $$$b = 0$ 、そしてすべての虚数は $$$a = 0$ 。

複素数の加算と減算

実数部と虚数部を加算および減算することにより、複素数を加算および減算できます。



追加：

$$

$$（a_1 + b_1i）+（a_2 + b_2i）=（a_1 + a_2）+（b_1 + b_2）i$$

減算：

$$

$$（a_1 + b_1i）-（a_2 + b_2i）=（a_1-a_2）+（b_1-b_2）i$$

複素数とスカラー値の乗算

複素数の各メンバーにスカラーを乗算することにより、複素数にスカラーが乗算されます。

$$

$$\ lambda（a + bi）= \ lambda {a} + \ lambda {b} i$$

複素数の積

さらに、通常の代数規則を使用して複素数を乗算することもできます。

$$

$$\ begin {array} {rcl} z_1＆=＆（a_1 + b_1i）\\ z_2＆=＆（a_2 + b_2i）\\ z_1z_2＆=＆（a_1 + b_1i）（a_2 + b_2i）\\＆=＆ a_1a_2 + a_1b_2i + b_1a_2i + b_1b_2i ^ 2 \\＆=＆（a_1a_2-b_1b_2）+（a_1b_2 + b_1a_2）i \ end {array}$$

複素数の二乗

また、複素数は、それ自体を乗算することで2乗できます。

$$

$$\ begin {array} {rcl} z＆=＆（a + bi）\\ z ^ 2＆=＆（a + bi）（a + bi）\\＆=＆（a ^ 2-b ^ 2） + 2abi \ end {array}$$

共役複素数

複素数の共役値は 、虚数部の符号が変更された複素数であり、 $$$\バー{z}$ またはどのように $$$z ^ *$ 。

$$

$$\ begin {array} {rcl} z＆=＆（a + bi）\\ z ^ *＆=＆（a-bi）\ end {array}$$

複素数とその共役値の乗算は興味深い結果をもたらします。

$$

$$\ begin {array} {rcl} z＆=＆（a + bi）\\ z ^ *＆=＆（a-bi）\\ zz ^ *＆=＆（a + bi）（a-bi）\ \＆=＆a ^ 2-abi + abi + b ^ 2 \\＆=＆a ^ 2 + b ^ 2 \ end {array}$$

複素数の絶対値

複素数の共役数を使用して、複素数の絶対値（またはnorm 、またはMagnitude ）を計算できます。 複素数の絶対値は、複素数の平方根とその共役の積です。 それは $$$| z |$ ：

$$

$$\ begin {array} {rcl} z＆=＆（a + bi）\\ | z | ＆=＆\ sqrt {zz ^ *} \\＆=＆\ sqrt {（a + bi）（a-bi）} \\＆=＆\ sqrt {a ^ 2 + b ^ 2} \ end {array}$$

2つの複素数の商

2つの複素数の商を計算するには、分子と分母に分母の共役数を掛けます。

$$

$$\ begin {array} {rcl} z_1＆=＆（a_1 + b_1i）\\ z_2＆=＆（a_2 + b_2i）\\ \ cfrac {z_1} {z_2}＆=＆\ cfrac {a_1 + b_1i} { a_2 + b_2i} \\＆=＆\ cfrac {（a_1 + b_1i）（a_2-b_2i）} {（a_2 + b_2i）（a_2-b_2i）} \\＆=＆\ cfrac {a_1a_2-a_1b_2i + b_1a_2i-bi ^ 2} {a_2 ^ 2 + b_2 ^ 2} \\＆=＆\ cfrac {a_1a_2 + b_1b_2} {a_2 ^ 2 + b_2 ^ 2} + \ cfrac {b_1a_2-a_1b_2} {a_2 ^ 2 + b_2 ^ 2} i \ end {array}$$

学位 $$$i$

私たちがそれを主張する場合 $$$i ^ 2 = -1$ その後の可能性がなければなりません $$$i$ 他の程度に。

$$

$$\ begin {array} {rrrrrrr} i ^ 0＆=＆＆＆＆＆＆＆1 \\ i ^ 1＆=＆＆＆＆＆＆i \\ i ^ 2＆=＆＆＆＆＆＆-1 \\ i ^ 3＆=＆ii ^ 2＆=＆＆＆-i \\ i ^ 4＆=＆i ^ {2} i ^ {2}＆=＆＆＆1 \\ i ^ 5＆=＆ii ^ 4 ＆=＆＆＆i \\ i ^ 6＆=＆ii ^ 5＆=＆i ^ 2＆=＆-1 \ end {array}$$

このシリーズを記録し続けると、パターンに気付くでしょう $$$（1、i、-1、-i、1、\ドット）$ 。



同様のパターンは、負の度合いの増加とともに発生します。

$$

$$\ begin {array} {rcr} i ^ 0＆=＆1 \\ i ^ {-1}＆=＆-i \\ i ^ {-2}＆=＆-1 \\ i ^ {-3} ＆=＆i \\ i ^ {-4}＆=＆1 \\ i ^ {-5}＆=＆-i \\ i ^ {-6}＆=＆-1 \ end {array}$$

あなたはすでに数学でこのパターンを見たかもしれませんが、 $$$（x、y、-x、-y、x、\ドット）$ 、2次元デカルト平面でポイントを反時計回りに90度回転することによって取得されます。 行 $$$（x、-y、-x、y、x、\ドット）$ 2次元デカルト平面上でポイントを90度回転させることにより作成されます。









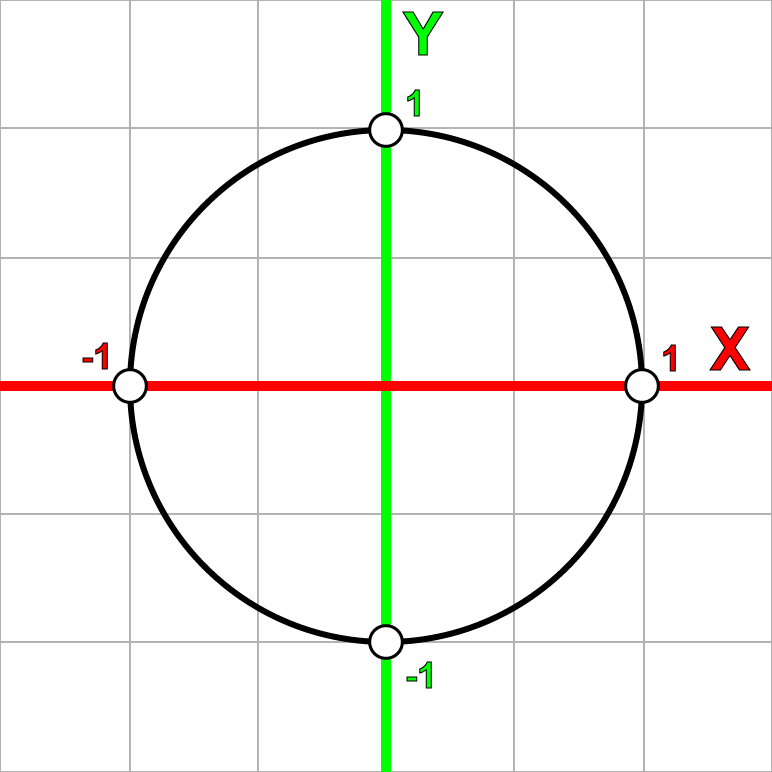
デカルト平面

複雑な飛行機

同様に、 複素数を複素平面と呼ばれる2次元グリッドに適用して、 実数部を水平軸に、 虚数部を垂直軸にリンクできます。









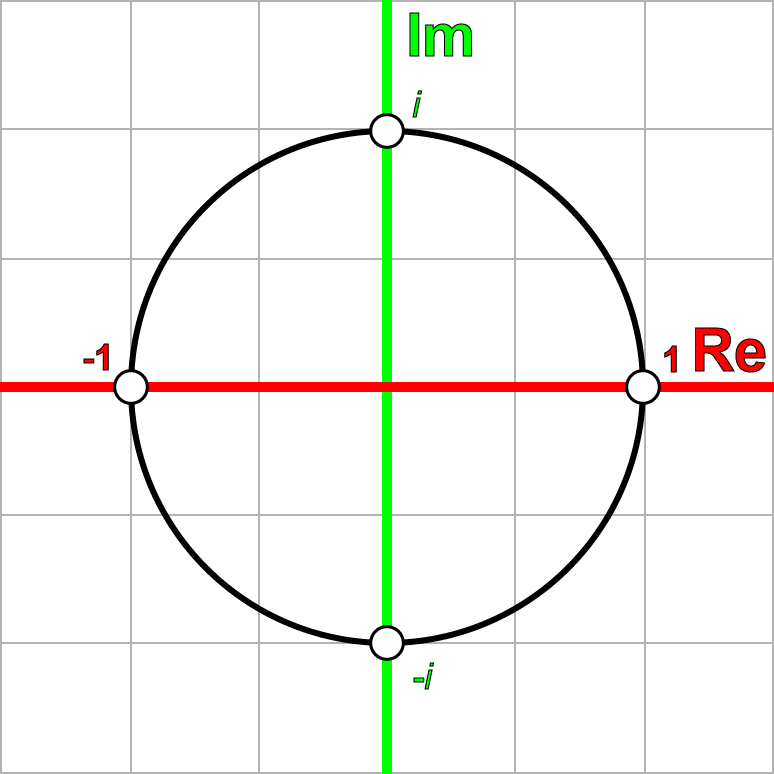
複雑な飛行機



前の行からわかるように、複素数を乗算すると $$$i$ 、その後、複素平面上で複素数を90度単位で回転させることができます。



これが正しいかどうかを確認しましょう。 複素平面上の任意の点を取ります $$$p$ ：

$$

$$p = 2 + i$$

そしてそれを掛けます $$$i$ 受け取った $$$q$ ：

$$

$$\ begin {array} {rcl} p＆=＆2 + i \\ q＆=＆pi \\＆=＆（2 + i）i \\＆=＆2i + i ^ 2 \\＆=＆- 1 + 2i \ end {array}$$

掛け算 $$$q$ に $$$i$ 私たちは得る $$$r$ ：

$$

$$\ begin {array} {rcl} q＆=＆-1 + 2i \\ r＆=＆qi \\＆=＆（-1 + 2i）i \\＆=＆-i + 2i ^ 2 \\＆ =＆-2-i \ end {array}$$

そして、乗算 $$$r$ に $$$i$ 私たちは得る $$$s$ ：

$$

$$\ begin {array} {rcl} r＆=＆-2-i \\ s＆=＆ri \\＆=＆（-2-i）i \\＆=＆-2i-i ^ 2 \\＆ =＆1-2i \ end {array}$$

そして、乗算 $$$s$ に $$$i$ 私たちは得る $$$t$ ：

$$

$$\ begin {array} {rcl} s＆=＆1-2i \\ t＆=＆si \\＆=＆（1-2i）i \\＆=＆i-2i ^ 2 \\＆=＆2 + i \ end {array}$$

そして、私たちは正確に始めたところに行きました $$$p$ ） これらの複素数を複素平面に配置すると、次の結果が得られます。









複素平面上の複素数



これで、複素平面上で時計回りに回転し、複素数に $$$-i$ 。

ローター

また、複素数を次の形式で設定することにより、複素平面上で任意のターンを実行できます。

$$

$$q = \ cos \ theta + i \ sin \ theta$$

複素数にローターを掛けるとき $$$q$ 一般式が得られます：

$$

$$\ begin {array} {rcl} p＆=＆a + bi \\ q＆=＆\ cos \ theta + i \ sin \ theta \\ pq＆=＆（a + bi）（\ cos \ theta + i \ sin \ theta）\\ a ^ {\ prime} + b ^ {\ prime} i＆=＆a \ cos \ theta-b \ sin \ theta +（a \ sin \ theta + b \ cos \ theta）i \終了{配列}$$

マトリックス形式で記述できるもの：

$$

$$\ begin {bmatrix} a ^ {\ prime}＆-b ^ {\ prime} \\ b ^ {\ prime}＆a ^ {\ prime} \ end {bmatrix} = \ begin {bmatrix} \ cos \ theta ＆-\ sin \ theta \\ \ sin \ theta＆\ cos \ theta \ end {bmatrix} \ begin {bmatrix} a＆-b \\ b＆a \ end {bmatrix}$$

原点を基準にして複素平面上の任意の点を反時計回りに回転させる方法は何ですか。

四元数

複素数のシステムと複素平面について学習したので、それらを3次元空間に持ち込むことができます。 $$$i$ さらに2つの虚数。



四元数の一般的な形式は次のとおりです

$$

$$q = s + xi + yj + zk ~~ s、x、y、z \ in \ mathbb {R}$$

ハミルトンの有名な表現によると：

$$

$$i ^ 2 = j ^ 2 = k ^ 2 = ijk = -1$$

$$

$$\ begin {array} {ccc} ij = k＆jk = i＆ki = j \\ ji = -k＆kj = -i＆ik = -j \ end {array}$$

の関係に気づくかもしれません $$$i$ 、 $$$j$ そして $$$k$ 単位デカルトベクトルのベクトル乗算のルールに非常に似ています。

$$

$$\ begin {array} {ccc} \ mathbf {x} \ times \ mathbf {y} = \ mathbf {z}＆\ mathbf {y} \ times \ mathbf {z} = \ mathbf {x}＆\ mathbf { z} \ times \ mathbf {x} = \ mathbf {y} \\ \ mathbf {y} \ times \ mathbf {x} =-\ mathbf {z}＆\ mathbf {z} \ times \ mathbf {y} = -\ mathbf {x}＆\ mathbf {x} \ times \ mathbf {z} =-\ mathbf {y} \ end {array}$$

ハミルトンはまた、その虚数 $$$i$ 、 $$$j$ そして $$$k$ 3つのデカルト単位ベクトルを表すために使用できます $$$\ mathbf {i}$ 、 $$$\ mathbf {j}$ そして $$$\ mathbf {k}$ 虚数と同じ性質を持つため、 $$$\ mathbf {i} ^ 2 = \ mathbf {j} ^ 2 = \ mathbf {k} ^ 2 = -1$ 。









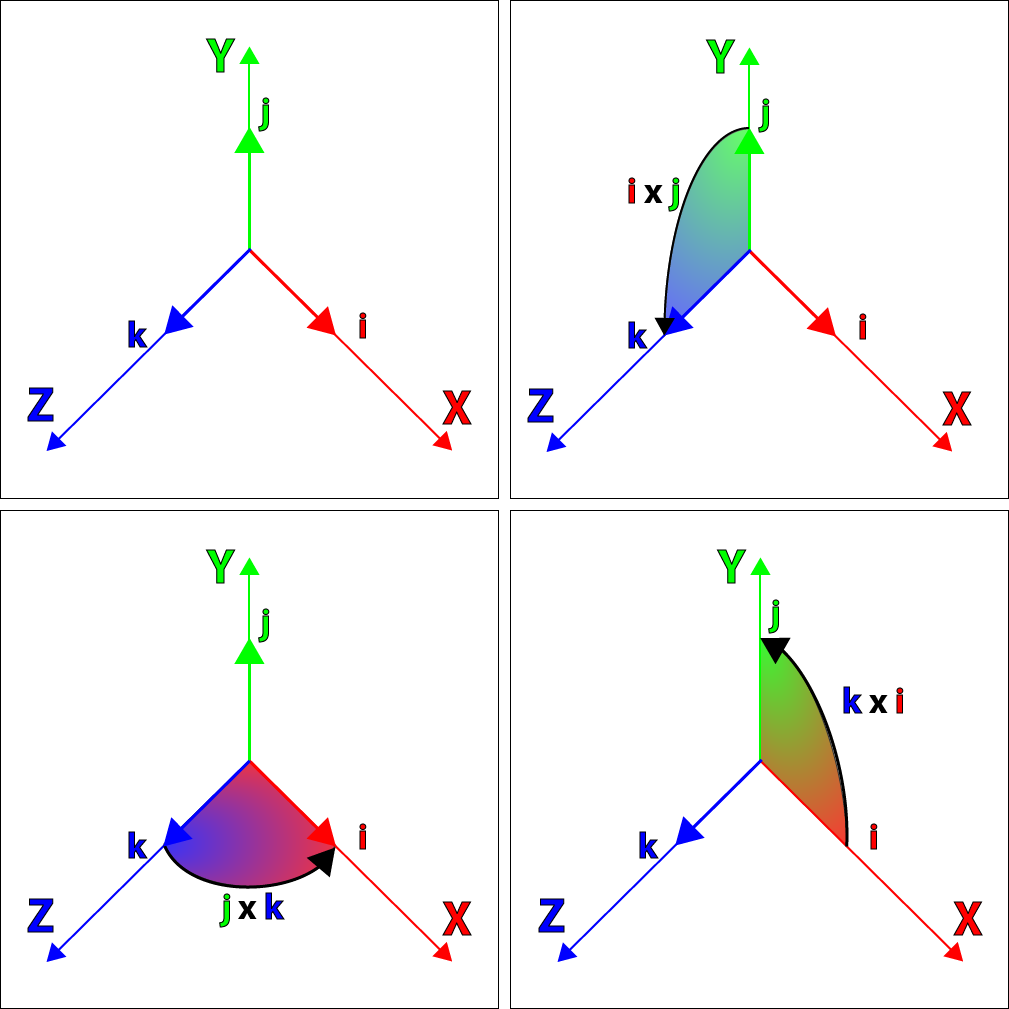
プロパティのグラフィカルな表現 $$$\ mathbf {ij}$ 、 $$$\ mathbf {jk}$ 、 $$$\ mathbf {ki}$



上の画像は、次の形式でデカルト単位ベクトル間の関係をグラフィカルに示しています $$$\ mathbf {i}$ 、 $$$\ mathbf {j}$ そして $$$\ mathbf {k}$ 。

順序ペアとしての四元数

四元数を順序付きペアとして表すこともできます。

$$

$$q = [s、\ mathbf {v}] ~~ s \ in \ mathbb {R}、\ mathbf {v} \ in \ mathbb {R} ^ 3$$

どこで $$$\ mathbf {v}$ 個々のコンポーネントとして表すこともできます。

$$

$$q = [s、x \ mathbf {i} + y \ mathbf {j} + z \ mathbf {k}] ~~ s、x、y、z \ in \ mathbb {R}$$

このエントリを使用すると、四元数と複素数の一般的な特徴をより簡単に表すことができます。

四元数の加算と減算

四元数は、複素数と同様に加算および減算できます。

$$

$$\ begin {array} {rcl} q_a＆=＆[s_a、\ mathbf {a}] \\ q_b＆=＆[s_b、\ mathbf {b}] \\ q_a + q_b＆=＆[s_a + s_b、 \ mathbf {a} + \ mathbf {b}] \\ q_a-q_b＆=＆[s_a-s_b、\ mathbf {a}-\ mathbf {b}] \ end {array}$$

クォータニオン作品

2つのクォータニオンの積も表現できます。

$$

$$\ begin {array} {rcl} q_a＆=＆[s_a、\ mathbf {a}] \\ q_b＆=＆[s_b、\ mathbf {b}] \\ q_ {a} q_ {b}＆=＆ [s_ {a}、\ mathbf {a}] [s_ {b}、\ mathbf {b}] \\＆=＆（s_ {a} + x_ {a} i + y_ {a} j + z_ {a } k）（s_ {b} + x_ {b} i + y_ {b} j + z_ {b} k）\\＆=＆（s_ {a} s_ {b} -x_ {a} x_ {b} -y_ {a} y_ {b} -z_ {a} z_ {b}）\\＆＆+（s_ {a} x_ {b} + s_ {b} x {a} + y_ {a} z_ {b } -y_ {b} z_ {a}）i \\＆＆+（s_ {a} y_ {b} + s_ {b} y_ {a} + z_ {a} x_ {b} -z_ {b} x_ {a}）j \\＆＆+（s_ {a} z_ {b} + s_ {b} z_ {a} + x_ {a} y_ {b} -x_ {b} y_ {a}）k \ end {配列}$$

これにより、別のクォータニオンが得られます。 前の式の虚数を置き換えると $$$i$ 、 $$$j$ そして $$$k$ 順序付きペア（クォータニオンユニットとも呼ばれます）を取得すると、

$$

$$i = [0、\ mathbf {i}]〜j = [0、\ mathbf {j}]〜k = [0、\ mathbf {k}]$$

そして、元の式に代入して $$$[1、\ mathbf {0}] = 1$ 私達は得る：

$$

$$\ begin {array} {rcl} [s_ {a}、\ mathbf {a}] [s_ {b}、\ mathbf {b}]＆=＆（s_ {a} s_ {b} -x_ {a} x_ {b} -y_ {a} y_ {b} -z_ {a} z_ {b}）[1、\ mathbf {0}] \\＆＆+（s_ {a} x_ {b} + s_ {b } x {a} + y_ {a} z_ {b} -y_ {b} z_ {a}）[0、\ mathbf {i}] \\＆＆+（s_ {a} y_ {b} + s_ { b} y_ {a} + z_ {a} x_ {b} -z_ {b} x_ {a}）[0、\ mathbf {j}] \\＆＆+（s_ {a} z_ {b} + s_ {b} z_ {a} + x_ {a} y_ {b} -x_ {b} y_ {a}）[0、\ mathbf {k}] \ end {array}$$

この式を順序付きペアの合計に展開すると、次のようになります。

$$

$$\ begin {array} {rcl} [s_ {a}、\ mathbf {a}] [s_ {b}、\ mathbf {b}]＆=＆[s_ {a} s_ {b} -x_ {a} x_ {b} -y_ {a} y_ {b} -z_ {a} z_ {b}、\ mathbf {0}] \\＆＆+ [0、（s_ {a} x_ {b} + s_ {b } x {a} + y_ {a} z_ {b} -y_ {b} z_ {a}）\ mathbf {i}] \\＆＆+ [0、（s_ {a} y_ {b} + s_ { b} y_ {a} + z_ {a} x_ {b} -z_ {b} x_ {a}）\ mathbf {j}] \\＆＆+ [0、（s_ {a} z_ {b} + s_ {b} z_ {a} + x_ {a} y_ {b} -x_ {b} y_ {a}）\ mathbf {k}] \ end {array}$$

四元数単位を掛けて共通ベクトル成分を抽出すると、この方程式を次のように書き換えることができます。

$$

$$\ begin {array} {rcl} [s_ {a}、\ mathbf {a}] [s_ {b}、\ mathbf {b}]＆=＆[s_ {a} s_ {b} -x_ {a} x_ {b} -y_ {a} y_ {b} -z_ {a} z_ {b}、\ mathbf {0}] \\＆＆+ [0、s_ {a}（x_ {b} \ mathbf {i } + y_ {b} \ mathbf {j} + z_ {b} \ mathbf {k}）+ s_ {b}（x_ {a} \ mathbf {i} + y_ {a} \ mathbf {j} + z_ { a} \ mathbf {k}）\\＆＆（y_ {a} z_ {b} -y_ {b} z_ {a}）\ mathbf {i} +（z_ {a} x_ {b} -z_ { b} x_ {a}）\ mathbf {j} +（x_ {a} y_ {b} -x_ {b} y_ {a}）\ mathbf {k}] \ end {array}$$

この方程式は、2つの順序付きペアの合計を示します。 最初の順序ペアは材料のクォータニオンで、2番目は純粋なクォータニオンです。 これらの2つの順序付きペアは、1つの順序付きペアに結合できます。

$$

$$\ begin {array} {rcl} [s_ {a}、\ mathbf {a}] [s_ {b}、\ mathbf {b}]＆=＆[s_ {a} s_ {b} -x_ {a} x_ {b} -y_ {a} y_ {b} -z_ {a} z_ {b}、\\＆＆s_ {a}（x_ {b} \ mathbf {i} + y_ {b} \ mathbf {j } + z_ {b} \ mathbf {k}）+ s_ {b}（x_ {a} \ mathbf {i} + y_ {a} \ mathbf {j} + z_ {a} \ mathbf {k}）\\ ＆＆+（y_ {a} z_ {b} -y_ {b} z_ {a}）\ mathbf {i} +（z_ {a} x_ {b} -z_ {b} x_ {a}）\ mathbf { j} +（x_ {a} y_ {b} -x_ {b} y_ {a}）\ mathbf {k}] \ end {array}$$

代入すると、

$$

$$\ begin {array} {rcl} \ mathbf {a}＆=＆x_ {a} \ mathbf {i} + y_ {a} \ mathbf {j} + z_ {a} \ mathbf {k} \\ \ mathbf {b}＆=＆x_ {b} \ mathbf {i} + y_ {b} \ mathbf {j} + z_ {b} \ mathbf {k} \\ \ mathbf {a} \ cdot \ mathbf {b}＆ =＆x_ {a} x_ {b} + y_ {a} y_ {b} + z_ {a} z_ {b} \\ \ mathbf {a} \ times \ mathbf {b}＆=＆（y_ {a} z_ {b} -y_ {b} z_ {a}）\ mathbf {i} +（z_ {a} x_ {b} -z_ {b} x_ {a}）\ mathbf {j} +（x_ {a} y_ {b} -x_ {b} y_ {a}）\ mathbf {k} \ end {array}$$

取得するもの：

$$

$$[s_ {a}、\ mathbf {a}] [s_ {b}、\ mathbf {b}] = [s_ {a} s_ {b}-\ mathbf {a} \ cdot \ mathbf {b}、s_ {a} \ mathbf {b} + s_ {b} \ mathbf {a} + \ mathbf {a} \ times \ mathbf {b}]$$

これは、四元数の積の一般的な方程式です。

リアルクォータニオン

実際のクォータニオンは、ベクトルが $$$\ mathbf {0}$ ：

$$

$$q = [s、\ mathbf {0}]$$

そして、2つのマテリアルクォータニオンの積は、別のマテリアルクォータニオンです。

$$

$$\ begin {array} {rcl} q_a＆=＆[s_a、\ mathbf {0}] \\ q_b＆=＆[s_b、\ mathbf {0}] \\ q_ {a} q_ {b}＆=＆ [s_a、\ mathbf {0}] [s_b、\ mathbf {0}] \\＆=＆[s_ {a} s_ {b}、\ mathbf {0}] \ end {array}$$

これは、虚数項を含む2つの複素数の積に似ています。

$$

$$\ begin {array} {rcl} z_1＆=＆a_1 + 0i \\ z_2＆=＆a_2 + 0i \\ z_ {1} z_ {2}＆=＆（a_1 + 0i）（a_2 + 0i）\\ ＆=＆a_ {1} a_ {2} \ end {array}$$

スカラー四元数乗算

次のルールを順守しながら、クォータニオンにスカラーを掛けることもできます。

$$

$$\ begin {array} {rcl} q＆=＆[s、\ mathbf {v}] \\ \ lambda {q}＆=＆\ lambda [s、\ mathbf {v}] \\＆=＆[\ラムダ{s}、\ラムダ\ mathbf {v}] \ end {array}$$

上記の実際のクォータニオンの積を使用して、クォータニオンに実際のクォータニオンとしてスカラーを掛けることにより、これを確認できます。

$$

$$\ begin {array} {rcl} q＆=＆[s、\ mathbf {v}] \\ \ lambda＆=＆[\ lambda、\ mathbf {0}] \\ \ lambda {q}＆=＆[ \ lambda、\ mathbf {0}] [s、\ mathbf {v}] \\＆=＆[\ lambda {s}、\ lambda \ mathbf {v}] \ end {array}$$

純粋な四元数

材料の四元数に加えて、ハミルトンは純粋な四元数をゼロスカラー項を持つ四元数として定義しました：

$$

$$q = [0、\ mathbf {v}]$$

または、コンポーネントを書き留める場合：

$$

$$q = xi + yj + zk$$

また、2つの純粋な四元数の積を取得できます。

$$

$$\ begin {array} {rcl} q_a＆=＆[0、\ mathbf {a}] \\ q_b＆=＆[0、\ mathbf {b}] \\ q_ {a} q_ {b}＆=＆ [0、\ mathbf {a}] [0、\ mathbf {b}] \\＆=＆[-\ mathbf {a} \ cdot \ mathbf {b}、\ mathbf {a} \ times \ mathbf {b} ] \ end {array}$$

上記のクォータニオンの積則に従って。

加算四元数形式

さらに、クォータニオンは、クォータニオンの実部と純粋部の合計として表現できます。

$$

$$\ begin {array} {rcl} q＆=＆[s、\ mathbf {v}] \\＆=＆[s、\ mathbf {0}] + [0、\ mathbf {v}] \ end {array }$$

単一四元数

任意のベクトルを取る $$$\ mathbf {v}$ 、このベクトルは、次のようにスカラー値と方向の両方で表現できます。

$$

$$\ mathbf {v} = v \ mathbf {\ hat {v}}〜\ text {where}〜v = | \ mathbf {v} |〜\ text {and}〜| \ mathbf {\ hat {v}} | = 1$$

この定義を純粋な四元数の定義と組み合わせると、次のようになります。

$$

$$\ begin {array} {rcl} q＆=＆[0、\ mathbf {v}] \\＆=＆[0、v \ mathbf {\ hat {v}}] \\＆=＆v [0、 \ mathbf {\ hat {v}}] \ end {array}$$

ゼロスカラーと単位ベクトルを持つ単位四元数を記述することもできます。

$$

$$\ hat {q} = [0、\ mathbf {\ hat {v}}]$$

四元数バイナリ形式

これで、単一の四元数の定義と四元数の加法形式を組み合わせて、複素数の説明で使用される表記法に似た形式の四元数を取得できます。

$$

$$\ begin {array} {rcl} q＆=＆[s、\ mathbf {v}] \\＆=＆[s、\ mathbf {0}] + [0、\ mathbf {v}] \\＆= ＆[s、\ mathbf {0}] + v [0、\ mathbf {\ hat {v}}] \\＆=＆s + v \ hat {q} \ end {array}$$

これは、四元数を複素数に非常によく似た形式で表す方法を提供します。

$$

$$\ begin {array} {rcl} z＆=＆a + bi \\ q＆=＆s + v \ hat {q} \ end {array}$$

四元数の共役数

四元数の共役数は、符号の反対側の四元数のベクトル部分を取ることで計算できます。

$$

$$\ begin {array} {rcl} q＆=＆[s、\ mathbf {v}] \\ q ^ *＆=＆[s、-\ mathbf {v}] \ end {array}$$

四元数とその共役数の積により、次のことがわかります。

$$

$$\ begin {array} {rcl} qq ^ *＆=＆[s、\ mathbf {v}] [s、-\ mathbf {v}] \\＆=＆[s ^ 2- \ mathbf {v} \ cdot- \ mathbf {v}、-s \ mathbf {v} + s \ mathbf {v} + \ mathbf {v} \ times- \ mathbf {v}] \\＆=＆[s ^ 2 + \ mathbf { v} \ cdot \ mathbf {v}、\ mathbf {0}] \\＆=＆[s ^ 2 + v ^ 2、\ mathbf {0}] \ end {array}$$

四元数ノルム

複素数のノルムの定義を思い出してください：

$$

$$\ begin {array} {rcl} | z | ＆=＆\ sqrt {a ^ 2 + b ^ 2} \\ zz ^ *＆=＆| z | ^ 2 \ end {array}$$

同様に、クォータニオンのノルム（または大きさ）は次のように定義されます。

$$

$$\ begin {array} {rcl} q＆=＆[s、\ mathbf {v}] \\ | q | ＆=＆\ sqrt {s ^ 2 + v ^ 2} \ end {array}$$

これにより、次のようにクォータニオンのノルムを表現できます。

$$

$$qq ^ * = | q | ^ 2$$

四元数の正規化

クォータニオンノルムの定義があれば、それを使用してクォータニオンを正規化できます。 四元数は、 $$$| q |$ ：

$$

$$q ^ {\ prime} = \ frac {q} {\ sqrt {s ^ 2 + v ^ 2}}$$

たとえば、クォータニオンを正規化しましょう：

$$

$$q = [1,4 \ mathbf {i} +4 \ mathbf {j} -4 \ mathbf {k}]$$

まず、四元数率を計算する必要があります。

$$

$$\ begin {array} {rcl} | q | ＆=＆\ sqrt {1 ^ 2 + 4 ^ 2 + 4 ^ 2 +（-4）^ 2} \\＆=＆\ sqrt {49} \\＆=＆7 \ end {array}$$

次に、正規化された四元数を計算するために、四元数を四元数のノルムで除算する必要があります。

$$

$$\ begin {array} {rcl} q ^ {\ prime}＆=＆\ cfrac {q} {| q |} \\ [1.0em]＆=＆\ cfrac {（1 + 4 \ mathbf {i} + 4 \ mathbf {j} -4 \ mathbf {k}）} {7} \\ [1.0em]＆=＆\ cfrac {1} {7} + \ cfrac {4} {7} \ mathbf {i} + \ cfrac {4} {7} \ mathbf {j}-\ cfrac {4} {7} \ mathbf {k} \ end {array}$$

逆四元数

逆四元数は $$$q ^ {-1}$ 。 逆四元数を計算するには、四元数の共役数を取り、それをノルムの二乗で除算します。

$$

$$q ^ {-1} = \ frac {q ^ *} {| q | ^ 2}$$

これを示すために、逆数の定義を使用できます。

$$

$$qq ^ {-1} = [1、\ mathbf {0}] = 1$$

そして、両側に四元数の共役数を掛けると、次のようになります。

$$

$$q ^ {*} qq ^ {-1} = q ^ {*}$$

置換により、以下が得られます。

$$

$$\ begin {array} {rcl} | q | ^ {2} q ^ {-1}＆=＆q ^ {*} \\ q ^ {-1}＆=＆\ cfrac {q ^ {*}} {| q | ^ {2}} \ end {array}$$

ノルムが1の単一の四元数ノルムの場合、次のように記述できます。

$$

$$q ^ {-1} = q ^ {*}$$

クォータニオンスカラープロダクト

ベクトルのスカラー積と同様に、対応するスカラー部分を乗算して結果を合計することにより、2つの四元数のスカラー積を計算できます。

$$

$$\ begin {array} {rcl} q_1＆=＆[s_1、x_1 \ mathbf {i} + y_1 \ mathbf {j} + z_1 \ mathbf {k}] \\ q_2＆=＆[s_2、x_2 \ mathbf { i} + y_2 \ mathbf {j} + z_2 \ mathbf {k}] \\ q_1 {\ cdot} q_2＆=＆s_ {1} s_ {2} + x_ {1} x_ {2} + y_ {1} y_ {2} + z_ {1} z_ {2} \ end {array}$$

四元数のスカラー積を使用して、四元数間の角度差を計算することもできます。

$$

$$\ cos \ theta = \ frac {s_ {1} s_ {2} + x_ {1} x_ {2} + y_ {1} y_ {2} + z_ {1} z_ {2}} {| q_ {1 } || q_ {2} |}$$

単一の四元数ノルムの場合、方程式を単純化できます。

$$

$$\ cos \ theta = s_ {1} s_ {2} + x_ {1} x_ {2} + y_ {1} y_ {2} + z_ {1} z_ {2}$$

ターン

ローターと呼ばれる特別な形式の複素数を特定したことを思い出してください。これは、次のように2次元平面上の点を回転させるために使用できます。

$$

$$q = \ cos \ theta + i \ sin \ theta$$

四元数との複素数の類似性により、四元数を表現することが可能になります。これは、3次元空間で点を回転するために使用できます。

$$

$$q = [\ cos \ theta、\ sin \ theta \ mathbf {v}]$$

四元数の積を計算して、この理論が正しいかどうかを確認しましょう $$$q$ およびベクトル $$$\ mathbf {p}$ 。 まず、表現することができます $$$\ mathbf {p}$ 次のように純粋な四元数として：

$$

$$p = [0、\ mathbf {p}]$$

A $$$q$ 次の形式の単一の四元数ノルムです。

$$

$$q = [s、\ lambda \ mathbf {\ hat {v}}]$$

それから

$$

$$\ begin {array} {rcl} p ^ {\ prime}＆=＆qp \\＆=＆[s、\ lambda \ mathbf {\ hat {v}}] [0、\ mathbf {p}] \\ ＆=＆[-\ lambda \ mathbf {\ hat {v}} \ cdot \ mathbf {p}、s \ mathbf {p} + \ lambda \ mathbf {\ hat {v}} \ times \ mathbf {p}] \ end {array}$$

結果は、スカラー部分とベクトル部分を持つ一般的な四元数であることがわかります。



最初に「特別な」ケースを見てみましょう。 $$$\ mathbf {p}$ 垂直 $$$\ mathbf {\ hat {v}}$ 。 この場合、スカラー積のメンバー $$$-\ lambda \ mathbf {\ hat {v}} \ cdot \ mathbf {p} = 0$ 結果は純粋な四元数になります：

$$

$$p ^ {\ prime} = [0、s \ mathbf {p} + \ lambda \ mathbf {\ hat {v}} \ times \ mathbf {p}]$$

この場合、 $$$\ mathbf {p}$ に関して $$$\ mathbf {\ hat {v}}$ 私たちはただ置き換える $$$s = \ cos \ theta$ そして $$$\ lambda = \ sin \ theta$ 。

$$

$$p ^ {\ prime} = [0、\ cos \ theta \ mathbf {p} + \ sin \ theta \ mathbf {\ hat {v}} \ times \ mathbf {p}]$$

たとえば、ベクトルを回転させましょう $$$\ mathbf {p}$ Z軸に対して45°。 その後、四元数 $$$q$ に等しくなります：

$$

$$\ begin {array} {rcl} q＆=＆[\ cos \ theta、\ sin \ theta \ mathbf {k}] \\＆=＆\ left [\ frac {\ sqrt {2}} {2}、 \ frac {\ sqrt {2}} {2} \ mathbf {k} \ right] \ end {array}$$

そして、ベクトルを取りましょう $$$\ mathbf {p}$ これは特別な場合に関連します $$$\ mathbf {p}$ 垂直 $$$\ mathbf {k}$ ：

$$

$$p = [0.2 \ mathbf {i}]$$

それでは作品を見つけましょう

$$

$$qp$$

：

$$

$$\ begin {array} {rcl} p ^ {\ prime}＆=＆qp \\＆=＆\ left [\ frac {\ sqrt {2}} {2}、\ frac {\ sqrt {2}} { 2} \ mathbf {k} \ right] [0.2 \ mathbf {i}] \\＆=＆\ left [0.2 \ frac {\ sqrt {2}} {2} \ mathbf {i} +2 \ frac {\ sqrt {2}} {2} \ mathbf {k} \ times \ mathbf {i} \ right] \\＆=＆[0、\ sqrt {2} \ mathbf {i} + \ sqrt {2 } \ mathbf {j}] \ end {array}$$

軸を中心に45°回転したきれいな四元数を与えるもの $$$\ mathbf {k}$ 。 最終ベクトルの値が保持されることを確認することもできます。

$$

$$\ begin {array} {rcl} | \ mathbf {p} ^ {\ prime} | ＆=＆\ sqrt {\ sqrt {2} ^ {2} + \ sqrt {2} ^ {2}} \\＆=＆2 \ end {array}$$

まさに私たちが期待したもの！



これを次の画像でグラフィカルに表示できます。









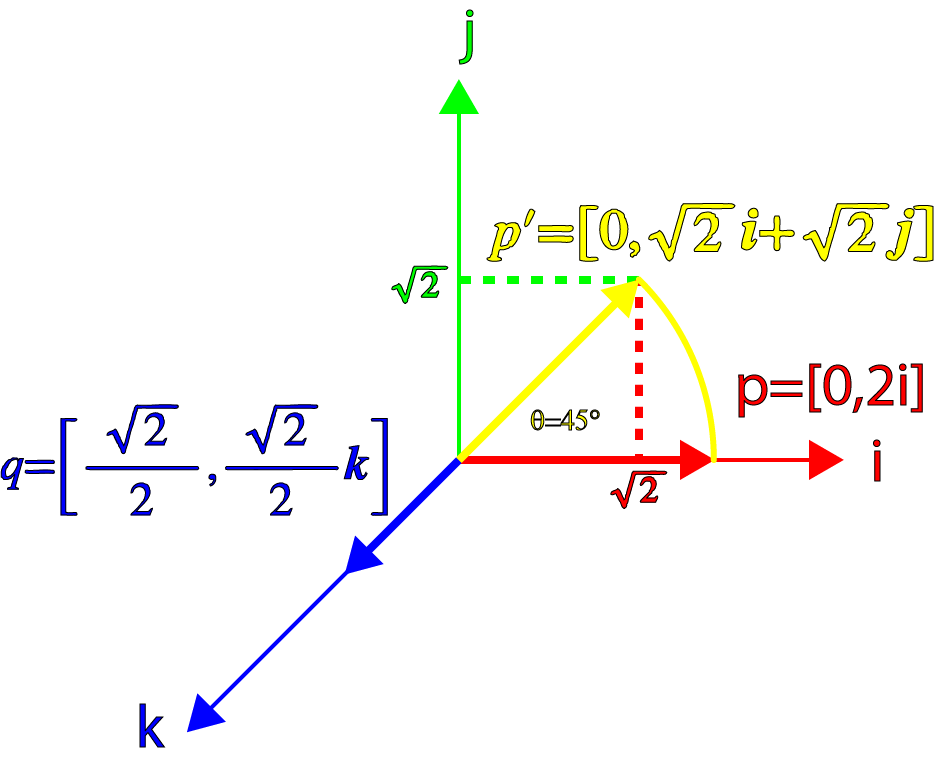
四元数の回転（1）



では、直交しないクォータニオンを見てみましょう $$$\ mathbf {p}$ 。 クォータニオンのベクトル部分について、45°のオフセットを $$$\ mathbf {p}$ 次に取得します：

$$

$$\ begin {array} {rcl} \ mathbf {\ hat {v}}＆=＆\ frac {\ sqrt {2}} {2} \ mathbf {i} + \ frac {\ sqrt {2}} {2 } \ mathbf {k} \\ \ mathbf {p}＆=＆2 \ mathbf {i} \\ q＆=＆[\ cos \ theta、\ sin \ theta \ mathbf {\ hat {v}}] \\ p＆=＆[0、\ mathbf {p}] \ end {array}$$

そして、ベクトルを掛けます $$$\ mathbf {p}$ に $$$q$ 私達は得る：

$$

$$\ begin {array} {rcl} p ^ {\ prime}＆=＆qp \\＆=＆[\ cos \ theta、sin \ theta \ mathbf {\ hat {v}}] [0、\ mathbf {p }] \\＆=＆[-\ sin \ theta \ mathbf {\ hat {v}} \ cdot \ mathbf {p}、\ cos \ theta \ mathbf {p} + \ sin \ theta \ mathbf {\ hat { v}} \ times \ mathbf {p}] \ end {array}$$

置換後 $$$\ mathbf {\ hat {v}}$ 、 $$$\ mathbf {p}$ そして $$$\ theta = 45 ^ {\ circ}$ 私達は得る：

$$

$$\ begin {array} {rcl} p ^ {\ prime}＆=＆\ left [-\ frac {\ sqrt {2}} {2} \ left（\ frac {\ sqrt {2}} {2} \ mathbf {i} + \ frac {\ sqrt {2}} {2} \ mathbf {k} \ right）\ cdot（2 \ mathbf {i}）、\ frac {\ sqrt {2}} {2} 2 \ mathbf {i} + \ frac {\ sqrt {2}} {2} \ left（\ frac {\ sqrt {2}} {2} \ mathbf {i} + \ frac {\ sqrt {2}} {2} \ mathbf {k} \ right）\ times2 \ mathbf {i} \ right] \\＆=＆[-1、\ sqrt {2} \ mathbf {i} + \ mathbf {j}] \ end {array}$$

つまり、それはもはや純粋な四元数ではなく、45°回転されておらず、ベクトルのノルムは2に等しくありません（それは $$$\ sqrt {3}$ ）



この結果はグラフィカルに表示できます。









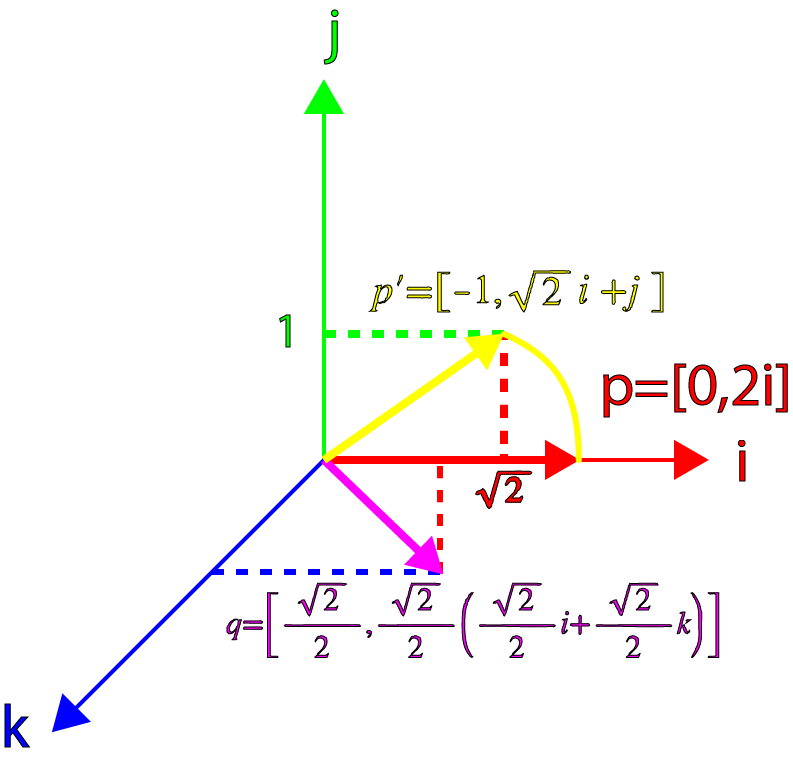
クォータニオンターン（2）

厳密に言えば、四元数を表すのは間違っています $$$p ^ {\ prime}$ なぜなら、実際には4次元のベクトルだからです！ 簡単にするために、クォータニオンのベクトルコンポーネントのみを示します。

ただし、すべてが失われるわけではありません。 ハミルトンは、結果を掛けると $$$qp$ 反対の値に $$$q$ 、結果は純粋な四元数になり、ベクトル成分のノルムが保持されます。 この例でこれを適用できるかどうか見てみましょう。



まず、計算しましょう $$$q ^ {-1}$ ：

$$

$$\ begin {array} {rcl} q＆=＆\ left [\ cos \ theta、\ sin \ theta \ left（\ frac {\ sqrt {2}} {2} \ mathbf {i} + \ frac {\ sqrt {2}} {2} \ mathbf {k} \ right）\ right] \\ q ^ {-1}＆=＆\ left [\ cos \ theta、-\ sin \ theta \ left（\ frac {\ sqrt {2}} {2} \ mathbf {i} + \ frac {\ sqrt {2}} {2} \ mathbf {k} \ right）\ right] \ end {array}$$

で $$$\ theta = 45 ^ {\ circ}$ 私達は得る：

$$

$$\ begin {array} {rcl} q ^ {-1}＆=＆\ left [\ frac {\ sqrt {2}} {2}、-\ frac {\ sqrt {2}} {2} \ left（ \ frac {\ sqrt {2}} {2} \ mathbf {i} + \ frac {\ sqrt {2}} {2} \ mathbf {k} \ right）\ right] \\＆=＆\ frac {1 } {2} \左[\ sqrt {2}、-\ mathbf {i}-\ mathbf {k} \右] \ end {array}$$

前の値を組み合わせる $$$qp$ そして $$$q ^ {-1}$ 私達は得る：

$$

$$\ begin {array} {rcl} qp＆=＆\ left [-1、\ sqrt {2} \ mathbf {i} + \ mathbf {j} \ right] \\ qpq ^ {-1}＆=＆\左[-1、\ sqrt {2} \ mathbf {i} + \ mathbf {j} \右] \ frac {1} {2} \左[\ sqrt {2}、-\ mathbf {i}-\ mathbf {k} \ right] \\＆=＆\ frac {1} {2} \ left [-\ sqrt {2}-\ left（\ sqrt {2} \ mathbf {i} + \ mathbf {j} \ right ）\ cdot（-\ mathbf {i}-\ mathbf {k}）、\ mathbf {i} + \ mathbf {k} + \ sqrt {2} \ left（\ sqrt {2} \ mathbf {i} + \ mathbf {j} \ right）-\ mathbf {i} + \ sqrt {2} \ mathbf {j} + \ mathbf {k} \ right] \\＆=＆\ frac {1} {2} \ left [- \ sqrt {2} + \ sqrt {2}、\ mathbf {i} + \ mathbf {k} +2 \ mathbf {i} + \ sqrt {2} \ mathbf {j}-\ mathbf {i} + \ sqrt {2} \ mathbf {j} + \ mathbf {k} \ right] \\＆=＆\ left [0、\ mathbf {i} + \ sqrt {2} \ mathbf {j} + \ mathbf {k} \右] \ end {array}$$

これは純粋な四元数であり、結果の標準は次のとおりです。

$$

$$\ begin {array} {rcl} | p ^ {\ prime} | ＆=＆\ sqrt {1 ^ 2 + \ sqrt {2} ^ 2 + 1 ^ 2} \\＆=＆\ sqrt {4} \\＆=＆2 \ end {array}$$

等しい $$$\ mathbf {p}$ 、つまり、ベクトルのノルムが保持されます。



下の画像は、回転の結果を示しています。









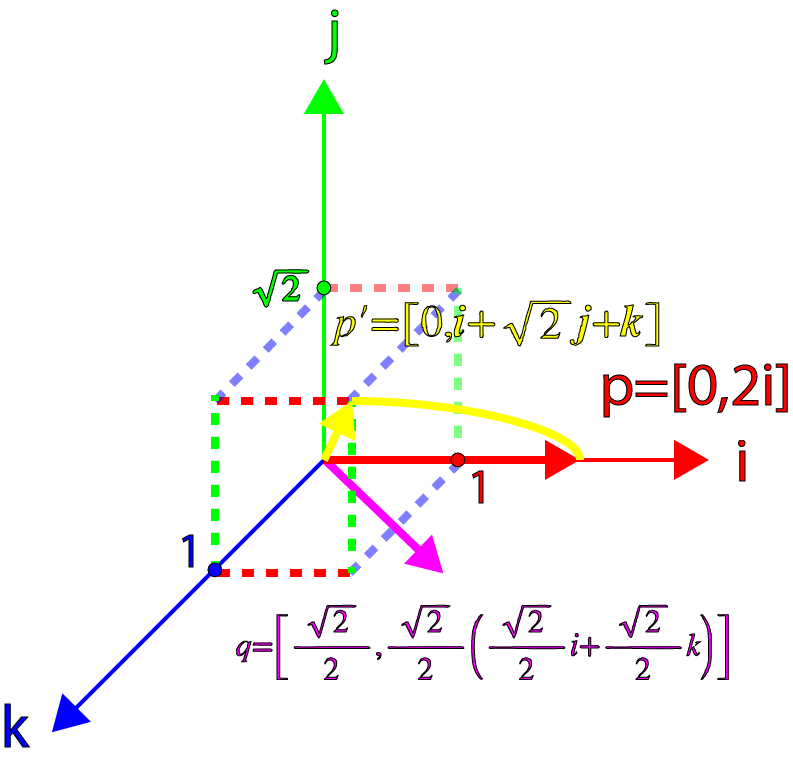
クォータニオンターン（3）



結果は純粋な四元数であり、元のベクトルのノルムは保持されていますが、ベクトルは必要な2倍である45°ではなく90°回転しています。 したがって、ベクトルの正しい回転のために $$$\ mathbf {p}$ 角に $$$\シータ$ 任意の軸に対して $$$\ mathbf {\ hat {v}}$ 半角を取り、次のクォータニオンを作成する必要があります。

$$

$$q = \左[\ cos \ frac {1} {2} \ theta、\ sin \ frac {1} {2} \ theta \ mathbf {\ hat {v}} \右]$$

クォータニオンターニングの一般的なビューとは何ですか！

四元数補間

コンピューターグラフィックスでクォータニオンを使用する最も重要な理由の1つは、クォータニオンが空間の回転を非常によく表現していることです。 四元数は、問題がオイラーコーナーの回転を表している折りたたみフレームなど、3D空間でポイントを回転させる他の方法の負担を取り除きます。



クォータニオンを使用して、3D空間での回転補間を表すいくつかの方法を定義できます。 私が検討している最初の方法はSLERPと呼ばれます 。 2つの方向の間のポイントをスムーズに補間するために使用されます。 2番目の方法はSLERPの開発であり 、 SQUADと呼ばれます。 パスを指定する一連の方向に沿って補間するために使用されます。

SLERP

SLERPは、Spherical L inear Interpolation（球面線形補間）の略です。 SLERPは、2つの方向の間のポイントをスムーズに補間する機能を提供します。



私は最初のオリエンテーションを $$$q_1$ 、および2番目の $$$q_2$ 。 補間された点は $$$\ mathbf {p}$ 、補間された点は $$$\ mathbf {p} ^ {\ prime}$ 。 補間パラメーター $$$t$ 補間します $$$\ mathbf {p}$ から $$$q_1$ で $$$t = 0$ 前に $$$q_2$ で $$$t = 1$ 。



標準の線形補間式は次のとおりです。

$$

$$\ mathbf {p} ^ {\ prime} = \ mathbf {p_1} + t（\ mathbf {p_2}-\ mathbf {p_1}）$$

この方程式を適用する基本的な手順は次のとおりです。

• の差を計算します $$$\ mathbf {p_1}$ そして $$$\ mathbf {p_2}$ 。
• この差の小数部分を取ります。
• 2つのポイント間のわずかな差によって初期値を修正します。

同じ基本原理を使用して、四元数の2つの方向の間を補間できます。

四元数の差

最初のステップは、以下の差を計算する必要があることを意味します $$$q_1$ そして $$$q_2$ 。 クォータニオンのコンテキストでは、これは2つのクォータニオン間の角度差を計算することに似ています。

$$

$$\デルタ{q} = q_1 ^ {-1} q_2$$

四元数を累乗する

次のステップは、この差の小数部分を取得することです。 クォータニオンの小数部を計算するには、値が範囲内の累乗になる $$$[0 ... 1]$ 。



クォータニオンを累乗する一般式は次の形式になります。

$$

$$q ^ t = \ exp（t \ log {q}）$$

四元数の指数関数は次のようになります。

$$

$$\ begin {array} {rcl} \ exp（q）＆=＆\ exp \ left（[0、\ theta \ mathbf {\ hat {v}}] \ right）\\＆=＆[\ cos \ theta 、\ sin \ theta \ mathbf {\ hat {v}}] \ end {array}$$

四元数の対数の形式は次のとおりです。

$$

$$\ begin {array} {rcl} \ log {q}＆=＆\ log（\ cos \ theta {+} \ sin \ theta \ mathbf {\ hat {v}}）\\＆=＆\ log \ left （\ exp（\ theta \ mathbf {\ hat {v}}）\右）\\＆=＆\ theta \ mathbf {\ hat {v}} \\＆=＆[0、\ theta \ mathbf {\ hat {v}}] \ end {array}$$

で $$$t = 0$ 次のものがあります。

$$

$$\ begin {array} {rcl} q ^ 0＆=＆\ exp（0 \ log {q}）\\＆=＆\ exp（[\ cos（0）、\ sin（0）\ mathbf {\ hat {v}}]）\\＆=＆\ exp（[1、\ mathbf {0}]）\\＆=＆[1、\ mathbf {0}] \ end {array}$$

そしていつ $$$t = 1$ 私たちは持っています

$$

$$\ begin {array} {rcl} q ^ 1＆=＆\ exp（\ log {q}）\\＆=＆q \ end {array}$$

四元数の分数差

補間された角回転を計算するには、初期の向きを変更します $$$q_1$ の差の小数部に $$$q_1$ そして $$$q_2$ 。

$$

$$q ^ {\ prime} = q_1 \左（q_1 ^ {-1} q_2 \右）^ t$$

四元数の球面線形補間の一般的なビューは何ですか。 ただし、これは実際に一般的に使用される種類のSLERP方程式ではありません。



同様の式を適用して、ベクトルの四元数への球面補間を実行できます。 ベクトルの球面補間の一般的な形式は次のように定義されます。

$$

$$\ mathbf {v} _t = \ frac {\ sin（1-t）\ theta} {\ sin \ theta} \ mathbf {v} _1 + \ frac {\ sin {t \ theta}} {\ sin \ theta} \ mathbf {v} _2$$

グラフィカルに、これは次の画像に示すことができます。









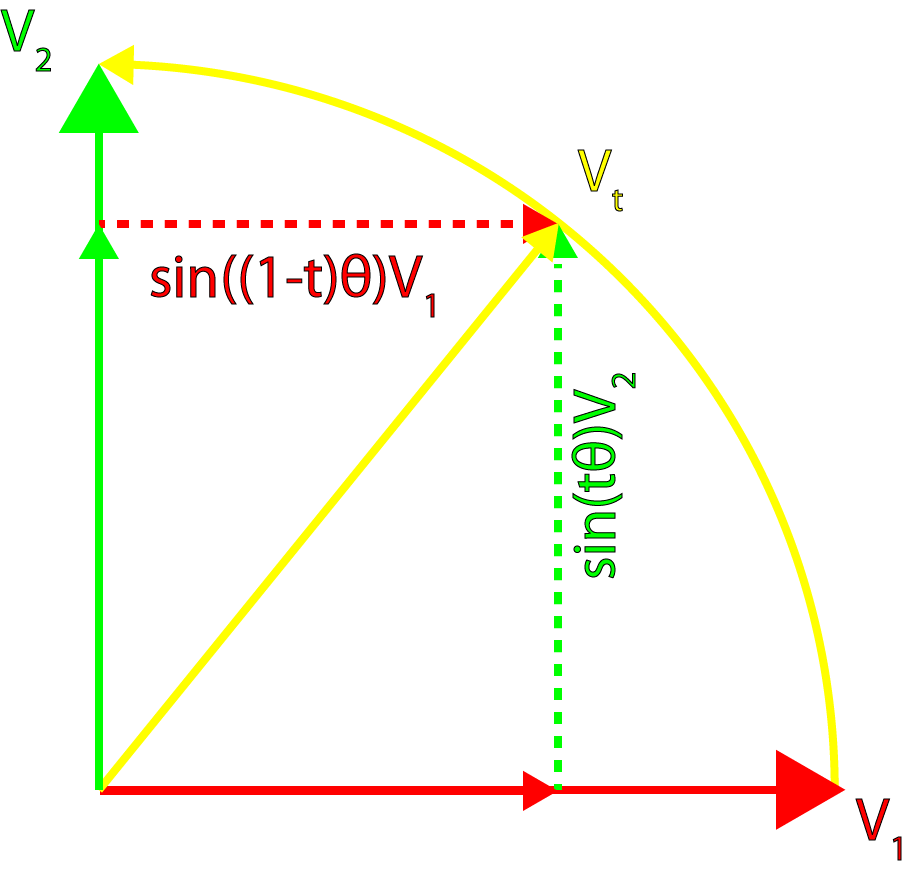
四元数補間



この式は、変更せずにクォータニオンに適用できます。

$$

$$q_t = \ frac {\ sin（1-t）\ theta} {\ sin \ theta} q_1 + \ frac {\ sin {t \ theta}} {\ sin \ theta} q_2$$

そして、角度を取得することができます $$$\シータ$ スカラー積の計算 $$$q_1$ そして $$$q_2$ 。

$$

$$\ begin {array} {rcl} \ cos \ theta＆=＆\ cfrac {q_1 {\ cdot} q_2} {| q_1 || q_2 |} \\＆=＆\ cfrac {s_ {1} s_ {2} + x_ {1} x_ {2} + y_ {1} y_ {2} + z_ {1} z_ {2}} {| q_1 || q_2 |} \\ \ theta＆=＆\ cos ^ {-1} \左（\ cfrac {s_ {1} s_ {2} + x_ {1} x_ {2} + y_ {1} y_ {2} + z_ {1} z_ {2}} {| q_1 || q_2 |} \右）\ end {array}$$

考慮すべき要素

この実装には、使用時に考慮すべき2つの問題があります。



第一に、四元数のスカラー積が負の値であることが判明した場合、補間は4次元の球で長く進みますが、これは必ずしも望ましいとは限りません。 この問題を解決するには、スカラー積の結果を確認し、それが負の場合、いずれかの方向と反対の値を取ることができます。 クォータニオンのスカラー部分とベクトル部分を反転しても、それらが表す方向は変わりませんが、これを行うことにより、回転が「最短」パスに沿って行われることが保証されます。



角度の差が $$$q_1$ そして $$$q_2$ とても小さい $$$\ sin \ theta$ 0になります。これが発生した場合は、 $$$\ sin \ theta$ 不確かな結果を得ることができます。 この場合、次の間の線形補間の使用に戻ることができます $$$q_1$ そして $$$q_2$ 。

分隊

SLERPを2つのクォータニオン間の補間に使用できるのと同様に、 SQUAD （ S球面および四角形のラング-球面および四角形）を使用して、回転経路に沿ったスムーズな補間を行うことができます。



四元数が多数ある場合：

$$

$$q_1、q_2、q_3、\ cdots、q_ {n-2}、q_ {n-1}、q_ {n}$$

そして、「補助」クォータニオン（ $$$s_i$ ）、これを中間制御点と見なすことができます：

$$

$$s_i = \ exp \ left（-\ frac {\ log \ left（q_ {i + 1} q_i ^ {-1} \ right）+ \ log \ left（q_ {i-1} q_i ^ {-1} \右）} {4} \右）q_i$$

曲線の一部に沿った方向は次のように定義されます：

$$

$$q_ {i-1}、q_i、q_ {i + 1}、q_ {i + 2}$$

時間tでこれは次のようになります。

$$

$$\ mathrm {squad}（q_i、q_ {i + 1}、s_i、s_ {i + 1}、t）= \ mathrm {slerp}（\ mathrm {slerp}（q_i、q_ {i + 1}、t ）、\ mathrm {slerp}（s_i、s_ {i + 1}、t）、2t（1-t））$$

おわりに

理解するのは困難ですが、ターンを操作する場合、四元数はオイラー行列と角度に対していくつかの明らかな利点を提供します。

• SLERPとSQUADを使用したクォータニオン補間は、空間の向きをスムーズに補間する方法を提供します。
• クォータニオンを使用した回転の連結は、マトリックス形式で表された回転を組み合わせるよりも高速です。
• 単一ノルムクォータニオンの場合、回転の逆数はクォータニオンのベクトル部分を減算することによって取得されます。 行列が正規直交でない場合、回転行列の逆数の計算ははるかに遅くなります（正規直交である場合、これは単なる行列の転置です）。
• 四元数の行列への変換は、オイラー角の場合よりもわずかに高速です。
• 回転を記述するために、クォータニオンには4つの数値（正規化されている場合は3つ。プログラム実行中に実数部を計算できます）だけが必要ですが、マトリックスには少なくとも9つの値が必要です。

ただし、クォータニオンを使用するすべての利点に加えて、いくつかの欠点もあります。

• 四元数は、浮動小数点数の丸め誤差により無効になる場合があります。 ただし、この「エラーのクリープ」は、クォータニオンを再正​​規化することで排除できます。
• おそらく、四元数の使用に対する最も重大な障害は、四元数の理解が非常に複雑であることです。 私の記事を読んでこの問題を解決してください。

四元数を実装する数学ライブラリは多数あり、そのうちの一部のみが四元数を正しく実装しています。 私自身の経験では、四元数の高品質な実装を備えた優れた数学ライブラリはGLM （OpenGL Math Library）です。 独自のアプリケーションでクォータニオンを使用する場合は、このライブラリをお勧めします。

デモをダウンロード

クォータニオンを使用して空間内のオブジェクトを回転させるデモを作成しました。 デモはUnity 3.5.2で作成されました。このエンジンを無料でダウンロードして、デモのソースコードを表示できます。 zipファイルにはWindowsバイナリ実行可能ファイルも含まれていますが、UnityではMac用のアプリケーションもビルドできます。



quaternions.zipを理解する

参照資料

ビンス、J（2011）。 コンピューターグラフィックスの四元数。 1日 編 ロンドン：スプリンガー。

Dunn、F. and Parberry、I.（2002）。 グラフィックスおよびゲーム開発用の3D Math Primer。 1日 編 テキサス州プラノ：Wordware Publishing、Inc.