アンリアルエンジン4チュートリアル：ペイントフィルター

時間の経過とともに、ゲームの外観はどんどん良くなります。 見事なグラフィックスの時代では、自分のゲームを他のゲームから際立たせることは困難です。 ゲームをグラフィカルにさらにユニークにする1つの方法は、非写実的なレンダリングを使用することです。



非写実的なレンダリングには、多くのレンダリング手法が含まれます。 これらには、セルシェーディング、漫画の輪郭、およびハッチングが含まれます。 ゲームを絵のように見せることもできます！ この効果を実現する1つの方法は、川原フィルタをぼかすことです。



Kawaharaフィルタリングを実装するために、次のことを学びます。

• 複数のコアの平均と分散を計算する
• 最小分散のカーネルの平均を出力します
• Sobel演算子を使用して、ピクセルのローカル方向を見つけます
• ローカルピクセルの方向に基づいてサンプリングコアを回転させる

注：このチュートリアルでは、Unreal Engineの基本をすでに理解していることを前提としています。 アンリアルエンジンを学んでいるだけなら、初心者向けの 10部構成のアンリアルエンジンチュートリアルシリーズをご覧ください。



このチュートリアルではHLSLを使用するため、C＃などのそれに似た言語に精通している必要があります。

注：このチュートリアルは、シェーダーに関する一連のチュートリアルの第4部です。

• パート1：セルシェーディング
• パート2：トゥーン回路
• パート3：カスタムHLSLシェーダー
• パート4：ペイントフィルター

仕事を始める

チュートリアル資料をダウンロードすることから始めます。 それらを解凍し、 PaintFilterStarterに移動してPaintFilter.uprojectを開きます 。 次のシーンが表示されます。









時間を節約するために、シーンにはすでにPP_Kuwaharaのポストプロセスボリュームがあります。 これは、変更するマテリアル（およびシェーダーファイル）です。









まず、Kawaharaフィルターとは何か、そしてどのように機能するかを理解しましょう。

川原フィルター

写真を撮るとき、画像にざらざらした質感があることに気付くでしょう。 これは私たちが絶対に必要としないノイズです。









通常、ノイズは、ぼかしなどのローパスフィルターを使用して除去されます。 以下は、半径5のボックスブラーを適用した後のノイズの多い画像です。









ほとんどのノイズは消えましたが、すべての境界線はシャープさを失いました。 画像を滑らかにしてオブジェクトの境界を保存できるフィルターがあればいいのに！



ご想像のとおり、カワハラフィルターはこれらの要件をすべて満たしています。 仕組みを見てみましょう。

川原フィルタリングの仕組み

畳み込みのように、カワハラフィルターはコアを使用しますが、1つではなく4つが使用されます。 コアは、1つのピクセルで（現在の）オーバーラップするように配置されます。 以下は、Kawaharaフィルターのコアの例です。









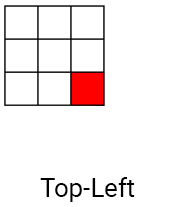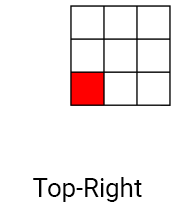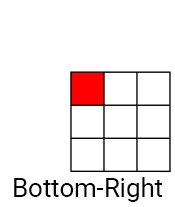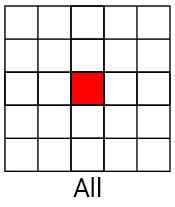
まず、各コアの平均 （平均色）を計算します。 そのため、コアをぼかす、つまりノイズを滑らかにします。



また、各コアについて、 分散を計算します。 実際、これはコアの色がどれだけ変化するかの尺度です。 たとえば、同系色のコアの分散は低くなります。 色が異なる場合、コアの分散は高くなります。

注：分散の概念に精通していない場合、またはその計算方法がわからない場合は、「数学の標準偏差と分散は楽しい」という記事をお読みください。

最後に、分散が最小のコアを見つけ、その平均値を導き出します。 分散に基づいた選択のおかげで、Kawaharaフィルターは境界を維持できます。 いくつかの例を見てみましょう。

川原ろ過の例

以下は、10x10のグレースケール画像です。 左下から右上の角に向かって、境界線があることがわかります。 また、画像の一部の領域にノイズが存在することに気付くかもしれません。









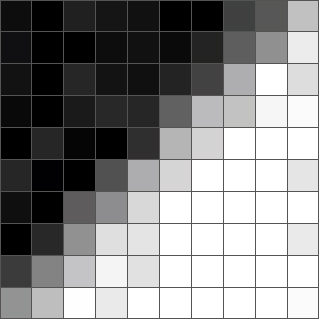
最初にピクセルを選択し、どのコアの分散が最小かを判断します。 境界線とその関連カーネルの隣のピクセルは次のとおりです。









ご覧のとおり、境界にある核の色は大きく異なります。 これは高分散について教えてくれ、フィルターがそれらを選択しないことを意味します。 境界線上にあるコアの選択を回避することにより、フィルターはぼやけた境界線の問題を排除します。



このピクセルの場合、フィルターは最も均一であるため、緑色のコアを選択します。 出力値は、緑のコアの平均値、つまり黒に近い色になります。



境界線とそのコアのもう1つのピクセルを次に示します。









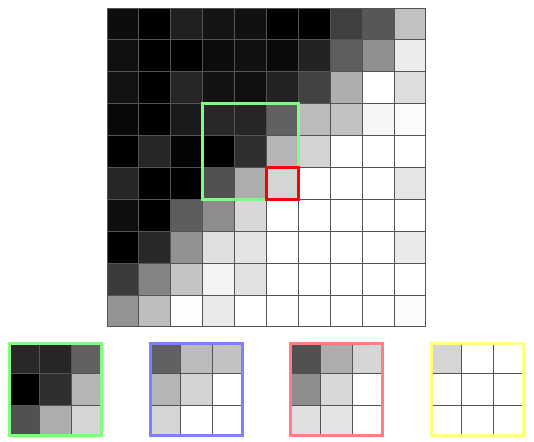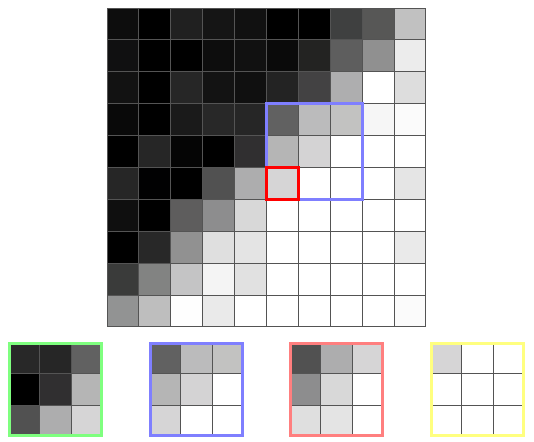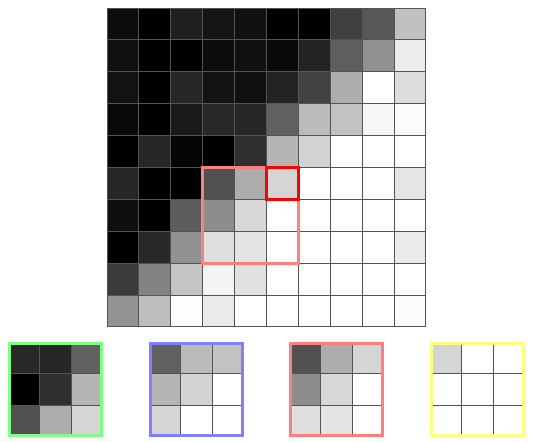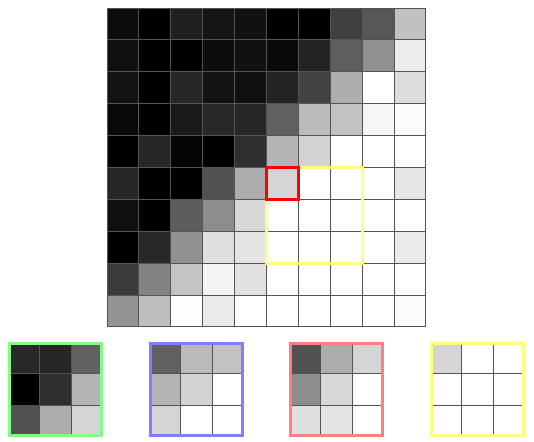
今回は、黄色のコアの分散が最小になります。これは、境界にない唯一のコアだからです。 したがって、出力値は黄色のコアの平均、つまり白に近い色になります。



以下は、ボックスブラーと半径5の川原フィルタリングの比較です。









ご覧のとおり、川原フィルタリングは、境界線を滑らかにして維持するという素晴らしい仕事をしています。 私たちの場合、フィルターは境界線をさらにシャープにしました！



偶然にも、境界線を保持するこのアンチエイリアシング機能は、画像にペイントされた画像の外観を与えることができます。 ブラシストロークは通常、シャープな境界線と低ノイズを生成するため、カワハラフィルターは現実的な画像を芸術的なスタイルに変換するのに便利な選択肢です。



可変サイズの川原フィルタリング写真の結果は次のとおりです。









かなりきれいですね。 Kawaharaフィルターの作成を始めましょう。

Kawaharaフィルターの作成

このチュートリアルでは、フィルターはGlobal.usfとKuwahara.usfの 2つのシェーダーファイルに分割されています。 最初のファイルには、カーネルの平均値と分散を計算する機能が含まれます。 2番目のファイルはフィルターエントリポイントで、各コアに対して上記の関数を呼び出します。



最初に、平均と分散を計算する関数を作成します。 OSでプロジェクトフォルダーを開き、 Shadersフォルダーに移動します。 次にGlobal.usfを開きます 。 内部には、 GetKernelMeanAndVariance()



関数があります。



関数の作成を開始する前に、追加のパラメーターが必要です。 関数のシグネチャを次のように変更します。

 float4 GetKernelMeanAndVariance(float2 UV, float4 Range)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

メッシュをサンプリングするには、2つのfor



が必要です。1つは水平オフセットです。 2つ目は垂直方向のものです。 最初の2つのRangeチャネルには、水平ループの境界が含まれます。 2番目の2つには、垂直サイクルの境界が含まれます。 たとえば、左上のコアをサンプリングし、フィルターの半径が2の場合、 Rangeの値は次のようになります。

 Range = float4(-2, 0, -2, 0);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

今こそサンプリングを開始する時です。

ピクセルサンプリング

まず、2つのfor



を作成する必要がありfor



。 GetKernelMeanAndVariance()



（変数の下GetKernelMeanAndVariance()



次のコードを追加します。

 for (int x = Range.x; x <= Range.y; x++) { for (int y = Range.z; y <= Range.w; y++) { } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これにより、すべてのコアオフセットが得られます。 たとえば、左上のコアをサンプリングし、フィルターの半径が2の場合、オフセットは（0、0）から（-2、-2）の範囲になります。









次に、サンプルピクセルの色を取得する必要があります。 次のコードを内側のfor



ループに追加for



ます。

 float2 Offset = float2(x, y) * TexelSize; float3 PixelColor = SceneTextureLookup(UV + Offset, 14, false).rgb;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最初の行は、サンプルピクセルのオフセットを取得し、UV空間に変換します。 2行目は、オフセットを使用してサンプルピクセルの色を取得します。



次に、平均と分散を計算する必要があります。

平均と分散の計算

平均の計算は非常に簡単なタスクです。 すべての色を単純に要約し、サンプル内のピクセル数で割るだけです。 分散については、次の式を使用します。ここで、 xはサンプルピクセルの色です。









最初に行う必要があるのは、金額の計算です。 平均を取得するには、変数Meanに色を追加するだけです。 分散を取得するには、色を2乗してからVarianceに追加する必要があります。 前のコードの下に次のコードを追加します。

 Mean += PixelColor; Variance += PixelColor * PixelColor; Samples++;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、 for



ループの後に次を追加for



ます。

 Mean /= Samples; Variance = Variance / Samples - Mean * Mean; float TotalVariance = Variance.r + Variance.g + Variance.b; return float4(Mean.r, Mean.g, Mean.b, TotalVariance);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最初の2行は、平均と分散を計算します。 ただし、問題が発生します。分散がRGBチャネル間で分散されます。 それを解決するために、3行目でチャネルをまとめて合計分散を取得します。



最後に、関数は平均と分散をfloat4として返します。 平均値はRGBチャンネルにあり、分散はチャンネルAにあります。



平均と分散を計算する関数ができたので、コアごとにそれを呼び出す必要があります。 Shadersフォルダーに戻り、 Kuwahara.usfを開きます。 まず、いくつかの変数を作成する必要があります。 内部のコードを次のものに置き換えます。

 float2 UV = GetDefaultSceneTextureUV(Parameters, 14); float4 MeanAndVariance[4]; float4 Range;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

各変数の用途は次のとおりです。

• UV：現在のピクセルのUV座標
• MeanAndVariance：各コアの平均と分散を保存する配列
• 範囲：現在のカーネルのfor
  
  
  
  ループの境界を格納するために使用

次に、コアごとにGetKernelMeanAndVariance()



を呼び出す必要があります。 これを行うには、次を追加します。

 Range = float4(-XRadius, 0, -YRadius, 0); MeanAndVariance[0] = GetKernelMeanAndVariance(UV, Range); Range = float4(0, XRadius, -YRadius, 0); MeanAndVariance[1] = GetKernelMeanAndVariance(UV, Range); Range = float4(-XRadius, 0, 0, YRadius); MeanAndVariance[2] = GetKernelMeanAndVariance(UV, Range); Range = float4(0, XRadius, 0, YRadius); MeanAndVariance[3] = GetKernelMeanAndVariance(UV, Range);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

したがって、各コアの平均と分散を次の順序で取得します：左上、右上、左下、右下。



次に、分散が最小のコアを選択し、その平均値を導出する必要があります。

最小分散カーネルの選択

分散が最小のカーネルを選択するには、次のコードを追加します。

 // 1 float3 FinalColor = MeanAndVariance[0].rgb; float MinimumVariance = MeanAndVariance[0].a; // 2 for (int i = 1; i < 4; i++) { if (MeanAndVariance[i].a < MinimumVariance) { FinalColor = MeanAndVariance[i].rgb; MinimumVariance = MeanAndVariance[i].a; } } return FinalColor;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

各部分の機能は次のとおりです。

1. 最終的な色と最小の分散を保持する2つの変数を作成します。 最初のコアの平均値と分散値でそれらの両方を初期化します。
2. 残りの3つのコアをループします。 現在のコアの分散が最小のものよりも低い場合、その平均と分散は新しいFinalColorとMinimumVarianceになります。 サイクルが完了すると、 FinalColorが表示されます。これは、分散が最小のカーネルの平均値になります。

Unrealに戻り、 Materials \ PostProcessに移動します。 PP_Kuwaharaを開き、 影響のない変更を加えて、[ 適用 ]をクリックします。 メインエディターに戻り、結果を確認します。









かなり良いように見えますが、よく見ると、画像に奇妙なブロック領域があることがわかります。 それらのいくつかを強調しました。









これは、軸と整列したカーネルを使用することの副作用です。 改良されたバージョンのフィルターを適用することで、この効果を減らすことができます 。これをKawahara Directional Filterと呼びます 。

川原方向性フィルター

このフィルターは元のフィルターと似ていますが、カーネルはローカルピクセルの方向に揃えられます。 Kawahara方向フィルターのカーネルの例を次に示します。

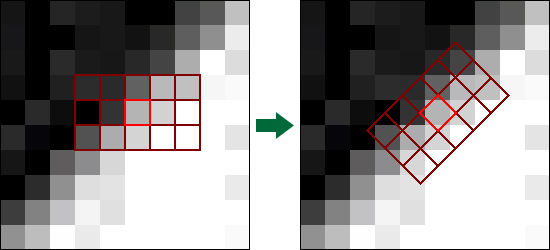
注：コアをマトリックスとして表現できるため、通常の幅x高さではなく高さx幅の形式で測定値を記録します。 マトリックスについては後で詳しく説明します。

ここで、フィルターは境界線に沿って配置されるようにピクセルの方向を決定します。 その後、コア全体を適宜回転させることができます。



ローカル方向を計算するために、フィルターはSobel演算子を使用して畳み込みを渡します。 「ソベル演算子」という用語がおなじみのように聞こえるのは、境界を認識するための一般的な手法だからです。 しかし、これが境界認識技術である場合、ローカルオリエンテーションを取得するためにどのように使用できますか？ この質問に答えるには、Sobel演算子の仕組みを理解する必要があります。

Sobelオペレーターの仕組み

1つのコアの代わりに、Sobelオペレーターは2つのコアを使用します。









Gxは水平方向の勾配を与えます。 Gyは垂直方向に勾配を与えます。 このような3×3グレースケール画像を例として使用してみましょう。









最初に、各コアの平均ピクセルを畳み込みます。









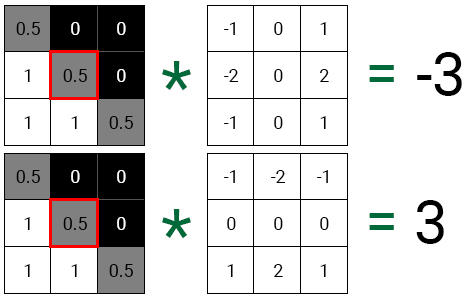
各値を2D平面に配置すると、結果のベクトルが境界と同じ方向を指すことがわかります。









ベクトルとX軸の間の角度を見つけるために、勾配の値をアークタンジェント関数（atan）に代入します。 次に、結果の角度を使用してコアを回転できます。



これが、Sobel演算子を使用してピクセルのローカル方向を取得する方法です。 やってみよう。

ローカルオリエンテーションを見つける

Global.usfを開き、 GetPixelAngle()



内に次のコードを追加します。

 float GradientX = 0; float GradientY = 0; float SobelX[9] = {-1, -2, -1, 0, 0, 0, 1, 2, 1}; float SobelY[9] = {-1, 0, 1, -2, 0, 2, -1, 0, 1}; int i = 0;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

注： GetPixelAngle()



最後のブラケットGetPixelAngle()



欠落していることに注意してください。 これは意図的に行われます！ これを行う理由を知りたい場合は、HLSLシェーダーに関するチュートリアルを参照してください。



各変数の用途は次のとおりです。

• GradientX：水平方向の勾配を保存します
• GradientY：垂直方向の勾配を保存します
• SobelX：配列としての水平Sobel演算子の中核
• SobelY：配列としての垂直Sobel演算子のコア
• i： SobelXおよびSobelYの各アイテムにアクセスするために使用

次に、 SobelXおよびSobelYコアを使用して畳み込みを行う必要があります。 次のコードを追加します。

 for (int x = -1; x <= 1; x++) { for (int y = -1; y <= 1; y++) { // 1 float2 Offset = float2(x, y) * TexelSize; float3 PixelColor = SceneTextureLookup(UV + Offset, 14, false).rgb; float PixelValue = dot(PixelColor, float3(0.3,0.59,0.11)); // 2 GradientX += PixelValue * SobelX[i]; GradientY += PixelValue * SobelY[i]; i++; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

各部分で何が起こるかを次に示します。

1. 最初の2行は、サンプルピクセルの色を取得します。 3行目は、彩度を下げ、グレーの濃淡の値に変換します。 これにより、各カラーチャネルの勾配を取得する代わりに、画像全体の勾配の計算が簡単になります。
2. 両方のコアについて、グレーの濃淡のピクセル値に対応するカーネル要素を掛けます。 次に、結果を対応する勾配変数に追加します。 次に、カーネルの次の要素のインデックスが含まれるように、増分iが発生します。

角度を取得するには、 atan()



関数を使用して、勾配値を置き換えます。 for



ループの下に、次のコードを追加します。

 return atan(GradientY / GradientX);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ピクセルの角度を取得する関数ができたので、カーネルを回転させるために何らかの方法でそれを適用する必要があります。 マトリックスを使用してこれを行うことができます。

マトリックスとは何ですか？

マトリックスは、数値の2次元配列です。 たとえば、次の2×3マトリックス（2行3列）です。









マトリックス自体は特に面白くありません。 しかし、行列をベクトルで乗算すると、行列の真の力が現れます。 これにより、（マトリックスのタイプに応じて）回転やスケーリングなどのアクションを実行できます。 しかし、回転のためのマトリックスをどのように作成しますか？



座標系では、各次元のベクトルがあります。 これらは、軸の正の方向を決定する基本ベクトルです。



以下は、2次元座標系のさまざまな基底ベクトルのいくつかの例です。 赤い矢印はXの正の方向を示します。緑の矢印はYの正の方向を示します。









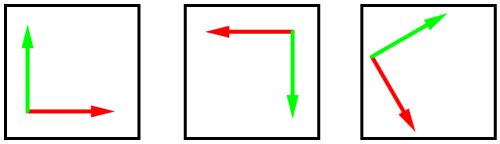
ベクトルを回転させるには、これらの基底ベクトルを使用して回転行列を作成します。 これは、回転後の基底ベクトルの位置を含む単純な行列です。 たとえば、座標（1、1 ）にベクトル（オレンジ色の矢印）があるとします。









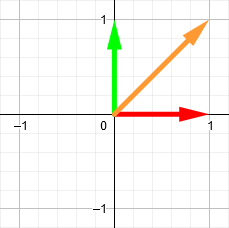
時計回りに90度回転させたいとします。 まず、基底ベクトルを同じ量だけ回転させます。









次に、基底ベクトルの新しい位置を使用して2×2行列を作成します。 最初の列は赤い矢印の位置で、2番目の列は緑の矢印の位置です。 これが回転行列です。









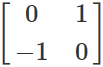
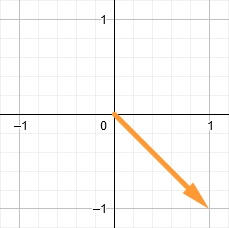
最後に、オレンジ色のベクトルと回転行列を使用して行列乗算を実行します。 結果は、オレンジ色のベクトルの新しい位置になります。

注： HLSLにはこのための組み込み関数があるため、行列乗算の実行方法を知る必要はありません。 しかし、知りたい場合は、Math is Funの「 行列を乗算する方法」の記事を参照してください。

それは素晴らしいことではありませんか？ しかし、さらに良いのは、上記のマトリックスを使用して、2Dベクトルを時計回りに90度回転できることです。 フィルターについて言えば、これは、各ピクセルの回転行列を一度作成し、それをコア全体に使用するのに十分であることを意味します。



次に、回転行列を使用してカーネルを回転させます。

コア回転

まず、 GetKernelMeanAndVariance()



を変更して、2×2マトリックスをGetKernelMeanAndVariance()



する必要があります。 これは、 Kuwahara.usfで回転行列を作成して転送するために必要です。 GetKernelMeanAndVariance()



署名を次のように変更します。

 float4 GetKernelMeanAndVariance(float2 UV, float4 Range, float2x2 RotationMatrix)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、内側のfor



ループの最初の行を次のコードに置き換えます。

 float2 Offset = mul(float2(x, y) * TexelSize, RotationMatrix);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

mul()



は、offsetとRotationMatrixを使用して行列乗算を行います。 したがって、現在のピクセルを中心にオフセットを回転させます。



次に、回転行列を作成する必要があります。

回転行列を作成する

回転行列を作成するには、次のように正弦関数と余弦関数を適用します。









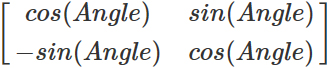
Global.usfを閉じ、 Kuwahara.usfを開きます。 次に、変数のリストの下に次を追加します。

 float Angle = GetPixelAngle(UV); float2x2 RotationMatrix = float2x2(cos(Angle), -sin(Angle), sin(Angle), cos(Angle));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最初の行は、現在のピクセルの角度を計算します。 2行目は、角度を使用して回転行列を作成します。



最後に、コアRotationMatrixごとに転送する必要があります。 GetKernelMeanAndVariance()



各呼び出しを次のように変更します。

 GetKernelMeanAndVariance(UV, Range, RotationMatrix)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、ここで川原方向性フィルターの作成が完了しました！ Kuwahara.usfを閉じてPP_Kuwaharaに戻ります。 何にも影響しない変更を加えるには、[ 適用 ]をクリックして閉じます。



以下の画像は、従来のカワハラフィルターと指向性カワハラフィルターの比較を示しています。 方向性フィルターはブロッキングを作成しないことに注意してください。

注： PPI_Kuwaharaを使用して、フィルターのサイズを変更できます。 Xに沿った半径がYに沿った半径よりも大きくなるようにフィルターのサイズを変更することをお勧めします。 これにより、境界に沿ってコアのサイズが大きくなり、指向性の作成に役立ちます。

次はどこへ行きますか？

完成したプロジェクトはこちらからダウンロードできます。



Kawaharaフィルターについて詳しく知りたい場合は、 異方性Kawaharaフィルターに関する記事を参照してください。 実際、川原方向性フィルターは、この記事で紹介したフィルターの簡易バージョンです。



マトリックスを使って新しいエフェクトを作成できるように、マトリックスを実験することをお勧めします。 たとえば、回転行列とぼかし行列の組み合わせを使用して、放射状または円形のぼかしを作成できます。 マトリックスとその仕組みの詳細については、3Blue1Brown Essence of Linear Algebraのビデオシリーズをご覧ください。