血管の中心線を検出する問題の解決策

タスクの本質

医療診断の過程で、患者の血管を検査する必要がある場合があります。 このような研究は血管造影と呼ばれます。 トモグラフの出現により、古典的な血管造影法に加えて、MRIおよびCT血管造影法が登場しました。これは、1つの投影で平坦な画像のみを提供する従来の血管造影法とは異なり、血管の完全な3次元表現を取得できます。 そのような研究を行うために、患者の血液にコントラストが導入されます。これは、写真の血管を明るくする特別な物質です。 提案された診断に応じて、医師は全体像を評価するか、問題が発生した血管の特定のセクションを見つけようとします。 血管の一部が狭くなり、血液の通過量が本来よりも少ない場合、この場所は狭窄と呼ばれます。









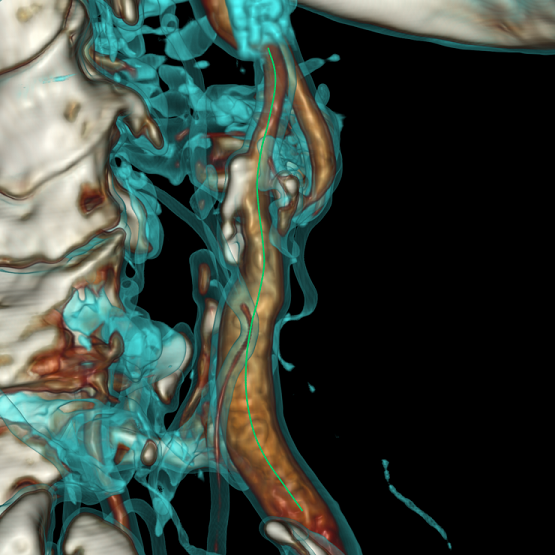
医師の仕事の1つは、狭窄を見つけて、その危険性を評価することです。 開発者のタスクは、通常どおり、エンドユーザーの作業を促進することです。 このためには、血管壁の完全な3Dモデルを構築し、初期解析を実施する必要があります。 これは大規模で興味深いタスクですが、より単純でよく知られている問題、つまり船の中心線の構築に基づいています。

最初の試み

この記事を読み続ける前に、断層撮影の作業の結果として得られたデータの表示に少し慣れることをお勧めします。 これは、 DICOMビューアのボクセルレンダリングに関する長年の記事を内側から読むことで実行できます。 要するに、信号の値（強度）が保存されている各要素には、数値の3D配列があります。 この配列はボリュームと呼ばれます。 要素自体はボクセルであり、3D配列内のそのインデックスは3D座標になります。 各ボクセルをレンダリングする前に、その強度は関数によって処理され、ボクセルは特定の色、明るさ、透明度を取得します。



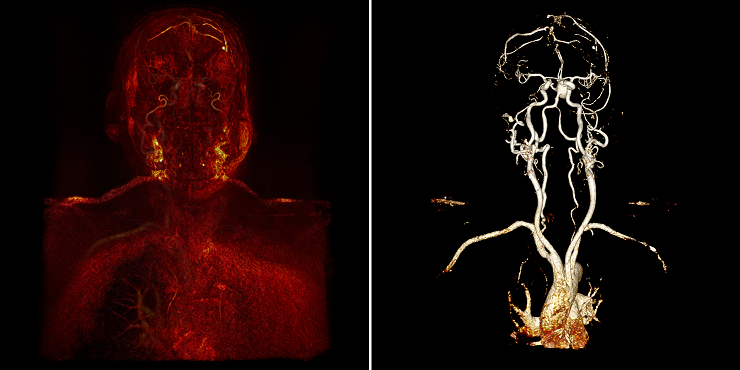
タスクに関して、私が最初に直面したのは、レンダリングによって視覚レベルですべての血管を表示できることです。 つまり、左の図のように理解できない「おridge」から、設定で遊んだ後、右の図のように非常に明白な容器を作成できます。









問題は解決されたようです：血管は「ここにあります」、領域成長アルゴリズムはすぐに思い浮かびます：必要なボクセルの色と透明度がわかっているので、指定されたポイント間のパスが敷設されるまで、近隣を反復処理できます。





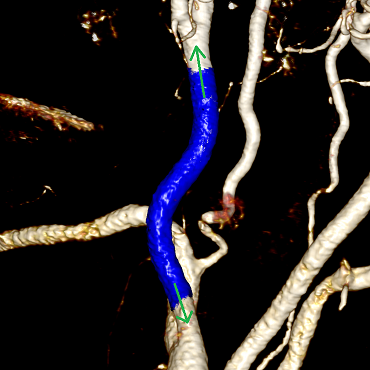
さらに、枝を扱う場合、船舶のネットワーク全体を拡張できるという考えがあります。 しかし、実際には、すべてがそれほど単純ではありません。 血管を骨に隣接させることができます（ボクセルの色は同じであるため、骨は血管の一部で知覚されます）。





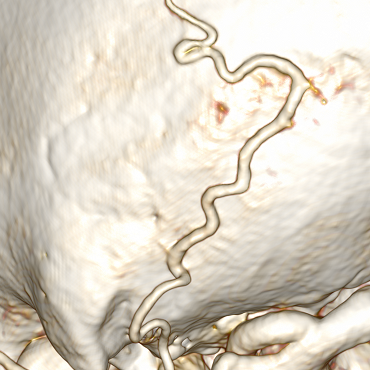
血管は曲がったり、近くに横たわったりする場合があります。





血管の一部は非常に薄く、さらには途切れることがあります。





最適なレンダリング設定を見つけるのは簡単です。 ユーザーはいわゆるウィンドウを変更することができ、少なくとも同じ研究のすべての血管に適した特定のウィンドウ値はありません。 ウィンドウは、特定のケースに合わせて毎回カスタマイズする必要があります。 以下は、設定が異なる同じ場所の3つのオプションです。









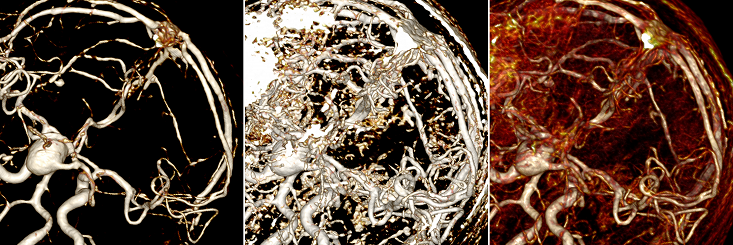
その結果、直感的に正しいと思われるアルゴリズムを変更するか、まったく異なるアプローチを試す必要があるという結論に達しました。 多くの失敗した試行の後、私は何か他のものを試みなければなりませんでした。

古典的なアプローチ

血管検出（血管検出）の問題に対する主なアプローチは、ヘッセ行列（ヘッセ行列）の固有値を計算することです。 また、最近、彼らはニューラルネットワークをこのタスクに接続しようとしています。 ただし、標準ソリューションはより多くの文献で言及されており、船舶の検出だけでなく、他の多くのタスク（天体画像での物体の検出など）にも使用されるため、信頼性が高いように見えるため、ニューラルネットワークを放棄する必要がありました。



私たちの場合、ヘッセ行列は、その要素が特定のボクセルの強度の2次の偏微分である行列です。

$$

$$H_ {M} = \ begin {pmatrix} \ frac {\ partial ^ 2 f} {\ partial ^ 2 x}＆\ frac {\ partial ^ 2 f} {\ partial x \ partial y}＆\ frac {\パーシャル^ 2 f} {\パーシャルx \パーシャルz} \\ \ frac {\パーシャル^ 2 f} {\パーシャルx \パーシャルy}＆\ frac {\パーシャル^ 2 f} {\パーシャル^ 2 y}＆ \ frac {\ partial ^ 2 f} {\ partial y \ partial z} \\ \ frac {\ partial ^ 2 f} {\ partial x \ partial z}＆\ frac {\ partial ^ 2 f} {\ partial y \ partial z}＆\ frac {\ partial ^ 2 f} {\ partial ^ 2 z} \ end {pmatrix}$$

-それぞれ、二次偏微分。



ヘッセ行列を作成した後、次の方程式を解いて固有値と固有ベクトルを見つける必要があります。

$$

$$\ begin {vmatrix} \ frac {\ partial ^ 2 f} {\ partial ^ 2 x}-\ lambda_ {1}＆\ frac {\ partial ^ 2 f} {\ partial x \ partial y}＆\ frac { \部分^ 2 f} {\部分x \部分z} \\ \ frac {\部分^ 2 f} {\部分x \部分y}および\ frac {\部分^ 2 f} {\部分^ 2 y} -\ lambda_ {2}＆\ frac {\ partial ^ 2 f} {\ partial y \ partial z} \\ \ frac {\ partial ^ 2 f} {\ partial x \ partial z}＆\ frac {\ partial ^ 2 f} {\ partial y \ partial z}＆\ frac {\ partial ^ 2 f} {\ partial ^ 2 z}-\ lambda_ {3} \ end {vmatrix} = 0$$

-固有値。 それらを見つける問題は3次方程式を解くことに帰着しますが、この場合、行列は対称であるため、解は単純化され、小さな擬似コードで表すことができます。

p1 = A(1,2)^2 + A(1,3)^2 + A(2,3)^2 if (p1 == 0) eig1 = A(1,1) eig2 = A(2,2) eig3 = A(3,3) else q = trace(A)/3 p2 = (A(1,1) - q)^2 + (A(2,2) - q)^2 + (A(3,3) - q)^2 + 2 * p1 p = sqrt(p2 / 6) B = (1 / p) * (A - q * I) r = det(B) / 2 if (r <= -1) phi = pi / 3 else if (r >= 1) phi = 0 else phi = acos(r) / 3 end eig1 = q + 2 * p * cos(phi) eig3 = q + 2 * p * cos(phi + (2*pi/3)) eig2 = 3 * q - eig1 - eig3 end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Aは元の3x3マトリックスです。 I-ユニット3x3マトリックス。 eig1、eig2、eig2-固有値; trace（）-マトリックスのトレースを返します。 det（）-行列の行列式を返します。



これで、固有ベクトルを見つけることができます。 これを行うには、方程式で：

$$

$$\ begin {vmatrix} \ frac {\ partial ^ 2 f} {\ partial ^ 2 x}-\ lambda＆\ frac {\ partial ^ 2 f} {\ partial x \ partial y}＆\ frac {\ partial ^ 2 f} {\ partial x \ partial z} \\ \ frac {\ partial ^ 2 f} {\ partial x \ partial y}＆\ frac {\ partial ^ 2 f} {\ partial ^ 2 y}-\ lambda ＆\ frac {\ partial ^ 2 f} {\ partial y \ partial z} \\ \ frac {\ partial ^ 2 f} {\ partial x \ partial z}＆\ frac {\ partial ^ 2 f} {\ partial y \部分的なz}＆\ frac {\部分的な^ 2 f} {\部分的な^ 2 z}-\ lambda \ end {vmatrix} \ cdot \ begin {vmatrix} V_ {x} \\ V_ {y} \\ V_ {z} \ end {vmatrix} = 0$$

代わりに、見つかった固有値の1つを置き換えます 。 見つかったベクトル そして固有ベクトルになります。 そのようなベクトルは3つあります。 -固有値ごとに1つ。 固有値とベクトルはこの順序でソートする必要があります 、ベクトルも場所を変更します。 値の交換 そして 私たちも交換します そして 。 ソート後に条件が満たされた場合 、マトリックスが構築されたボクセルは血管に属すると考えられています。 さらに、固有ベクトル ボクセルが壁にどれだけ近くても、血管に沿った方向を示します。









ボクセルが血管に属する場合、いわゆる血管分布は、マトリックスの固有値に基づいて計算されます。 文献にはさまざまな公式がありますが、そのうちの1つを自分用に適合させました。

$$

$$V _ {\ sigma} = \左（1- \ frac {{\ lvert} {\ lvert} \ lambda_ {2} {\ rvert}-{\ lvert} \ lambda_ {3} {\ rvert} {\ rvert} } {{\ lvert} \ lambda_ {2} {\ rvert} + {\ lvert} \ lambda_ {3} {\ rvert}} \ right）\ cdot \ left（\ lambda_ {1} \ frac {2} {3 }-\ lambda_ {2}-\ lambda_ {3} \ right）\ cdot \ left（1-e ^ {-\ frac {{\ lambda_ {1}} ^ 2 + {\ lambda_ {2}} ^ 2+ {\ lambda_ {3}} ^ 2} {2}} \右）$$

-したがって、血管の価値



血管が大きいほど、ボクセルは血管の中心に近くなります。 与えられたボクセルから中心線を見つけるための簡単なアルゴリズムを想像するのは簡単です：

1. 現在のボクセル内の血管の方向を決定し、
2. 血管の断面を方向に垂直に作成し、勾配に沿って最大血管密度の断面ボクセルに移動します。
3. ボクセル内の血管の方向を最大血管度で決定し、
4. 血管の方向に小さな一歩を踏み出し、新しいボクセルに落ちます。
5. 手順1に戻ります。

どちらが必要かを前もって知ることができないため、最初の時点から、移動は2つの方向に発生します。





その結果、最も美しいものではなく、正しい中心線が得られます。







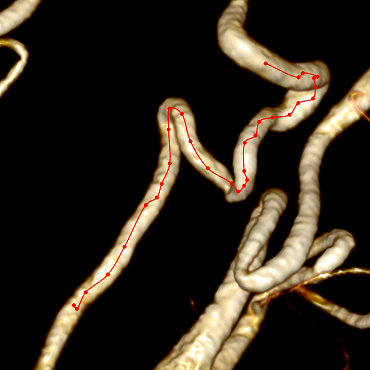
中心線の角度を小さくするには、ボクセルの整数座標を放棄し、3D空間のポイントの小数座標に移動する必要があります。また、構築後に中心線のわずかな平滑化を実行することもできます。



分数座標に移動するには、バイキュービック補間を使用して強度値を取得しました。 1次元空間でのフィルターの一般式は次のとおりです。

$$

$$k（x）= \ frac {1} {6} \ begin {cases}（12-9B-6C）\ lvert {x} \ rvert ^ 3 +（-18 + 12B + 6C）\ lvert {x} \ rvert ^ 2 +（6-2B）、\ quad if \> \ lvert {x} \ rvert <1 \\（-B-6C）\ lvert {x} \ rvert ^ 3 +（6B + 30C）\ lvert { x} \ rvert ^ 2 +（-12B-48C）\ lvert {x} \ rvert +（8B + 24C）、\\> \> 1 \ leq \ lvert {x} \ rvert <2 \\ 0、\ quad \ end {cases}$$

どこで そして 定義済みの値があります。 もし 次に、Bスプラインを扱っています。 、次に基本スプラインを使用します。 私たちの場合 、 （Catmull-Romフィルター）。 それから私達は得る：

$$

$$k（x）= \ frac {1} {6} \ begin {cases} 9 \ lvert {x} \ rvert ^ 3-15 \ lvert {x} \ rvert ^ 2 + 6、\ quad if \> \ lvert {x} \ rvert <1 \\-3 \ lvert {x} \ rvert ^ 3 + 15 \ lvert {x} \ rvert ^ 2-24 \ lvert {x} \ rvert + 12、\ quad if \> 1 \ leq \ lvert {x} \ rvert <2 \\ 0、\ quadそれ以外の場合\ end {cases}$$

1Dの場合を検討してください。 値がポイントで指定されている場合 座標付き 補間します どこで 、それから各頂点の重みを計算できます：

$$

$$\\ w _ {-1}（x）= \ frac {1} {2}（x ^ 2（2-x）-x）\\ w_ {0}（x）= \ frac {1} {2} （x ^ 2（3x-5）+2）\\ w_ {1}（x）= \ frac {1} {2}（x ^ 2（4-3x）+ x）\\ w_ {2}（x ）= \ frac {1} {2} x ^ 2（x-1）$$

最終的な補間値：

$$

$$f（x）= p _ {-1} \ cdot w _ {-1}（x）+ p_ {0} \ cdot w_ {0}（x）+ p_ {1} \ cdot w_ {1}（x）+ p_ {2} \ cdot w_ {2}（x）$$

次に、3D空間の完全なケースを検討します。 ご想像のとおり、4x4x4ボクセルディメンションのキューブ内に補間します。 基礎として、1Dケースで考慮される重みを使用します。

$$

$$f（x_ {0}、y_ {0}、z_ {0}）= \ sum_ {i = -1} ^ {2} \ sum_ {j = -1} ^ {2} \ sum_ {k = -1 } ^ {2} w_ {i}（x_ {0}-\ lfloor x_ {0} \ rfloor）\ cdot w_ {j}（y_ {0}-\ lfloor y_ {0} \ rfloor）\ cdot w_ {k }（z_ {0}-\ lfloor z_ {0} \ rfloor）\ cdot \\\ cdot I（\ lfloor x_ {0} \ rfloor + i、\ lfloor y_ {0} \ rfloor + j、\ lfloor z_ { 0} \ rfloor + k）$$

どこで -ポイントの小数座標、 -座標を持つボクセルの強度 、 -切り捨て。



一部の人にとっては、すべてのボクセルの重みの合計が1であることは興味深いように思えるかもしれません。

$$

$$\ sum_ {i = -1} ^ {2} \ sum_ {j = -1} ^ {2} \ sum_ {k = -1} ^ {2} w_ {i}（x- \ lfloor x \ rfloor） \ cdot w_ {j}（y- \ lfloor y \ rfloor）\ cdot w_ {k}（z- \ lfloor z \ rfloor）= 1$$

詳細

ヘッセ行列の導関数の計算に戻りましょう。 二次偏導関数は数値的であるとみなされるため、座標と強度があります。誰もが知っていることです。主なものは有限差分法です。 ポイントについて ：





ノイズを除去するには、導関数を計算する前に、特定の値でガウス平滑化を実行する必要があります 次に、平滑化された強度値から既に特定の点でヘッセ行列を計算します。 ある点でのガウス平滑化 ：

$$

$$G（x_ {0}、y_ {0}、z_ {0}）= \ sum_ {i = -r} ^ {r} \ sum_ {j = -r} ^ {r} \ sum_ {k = -r } ^ {r} I（x_ {0} + i、y_ {0} + j、z_ {0} + k）\ cdot \ frac {1} {（2 \ pi）^ \ frac {3} {2} \ sigma ^ 3} \ cdot {e} ^ {-\ frac {i ^ 2 + j ^ 2 + k ^ 2} {2 \ sigma ^ 2}}$$

どこで 点での強度の値を返します ; 通常は価値があります （ -切り上げ）; -平滑化係数。



平滑化前、平滑化後の血管の垂直断面の強度値、3番目の図では、血管分布値：









また、 値が大きいほど 私たちは見つけようとしている太い血管を使います 。 そして、一般的にすべての容器が必要であるため、細くても太くても、多くの意味が必要です。 、各値に対して平滑化を実行する必要があります。 範囲に決着しました 10個の値が含まれます。



しかし、成長とともに 二次導関数の値は減少します。 これは、順番に、血管新生が大きいと計算されたという事実につながります 血管が少なく、同じポイントで計算され、小さい 、実際には太い容器を扱っています。 実像に関係なく、細い血管に似た構造が常に優勢であることが判明しました。 したがって、問題が発生します：それぞれの結果の血管性を互いに関連付ける方法 ？ これを行うには、計算の結果を正規化する必要があります。 文献では、結果として生じる血管性を伴う操作が通常実行されます、例えば：



どこで -正規化された血管、 -平滑化のために得られた血管分布 、 実験的に選択した場合、適切なオプションは0.5です。



いわゆるガンマ正規化を使用しました。 どこで -ヘッセ行列 導関数の順序、つまり 2 私たちの場合、実験的に選択された0.5オプションは、それ自体がよく表れています。 次に、式全体が 。



さて、血管新生の値を小さな値で計算しようとすると 完全に細い血管の中心にある場合、血管の値とほぼ等しくなり、 完全に厚い容器の中心に。



中心線を作成するときの任意の点の計算アルゴリズムは次のようになります。

1. • 値を選択 ポイントとその近傍で滑らかにします（これらは微分を計算するために必要です）、
   • 二次導関数を計算し、ヘッセ行列を作成します。
   • ヘッセ行列を乗算して正規化します 、固有値を見つける
     
     
   • 血管分布を計算する
   • 未使用の場合 、その後、先頭に戻り、そうでない場合はポイント2に進みます。
2. 血管分布が最大であることが判明したヘッセ行列の固有ベクトルを計算し、血管の方向ベクトルを取得します。

このアルゴリズムと中心線を構成するアルゴリズムを組み合わせて、最終結果を取得します。

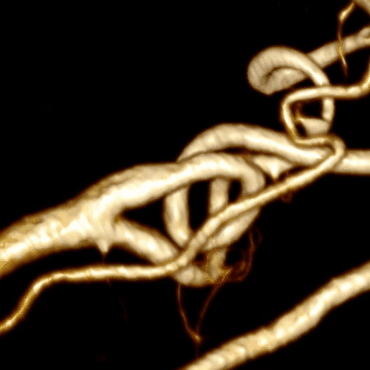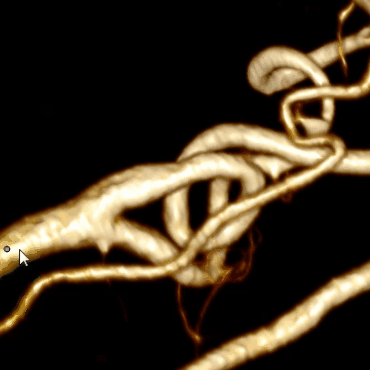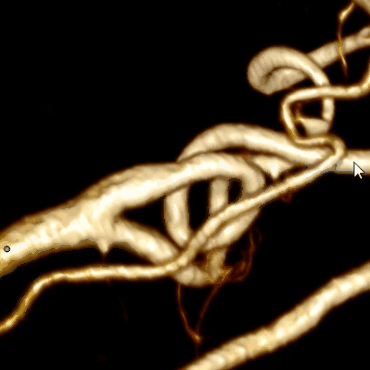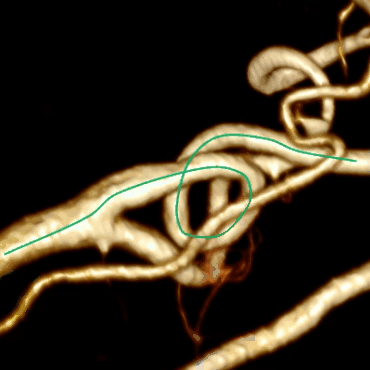
最適化

上記のアプローチはうまく機能しますが、いくつかのポイントがあります。 まず、パフォーマンスを向上させるには、すべてのボクセルとすべてのボクセルに対して事前にスムージングを実行する必要があります 。 次に、調査のサイズは通常約512x512x512ボクセルであるという事実を考慮すると、平滑化結果を保存するために必要なメモリサイズは平均で約5 GBを占有します。 使用されるメモリの量を減らすために、ピラミッド（スケールスペースピラミッド）を使用しました。



これは、各スムージングの後、隣接するボクセルの強度値がぼやけてほぼ等しくなるため、それらすべてを保存する意味がないためです。 つまり もっと 、ボリューム全体の平滑化を復元するために計算されたボクセルが必要になることは少なくなります。



一般的に、このように機能します。 ボリュームのゼロレイヤーはオリジナルです。 平滑化フィルター（¼、½、¼）が各ボリューム軸に沿って数回適用され、その後、ボリュームの次元が半分になります。 結果のボリュームは最初のレイヤーに属します。 その後、操作が繰り返され、2番目のレイヤーが取得されます。 その後、3番目など 各層には特定の値があります。 。 2Dの例：







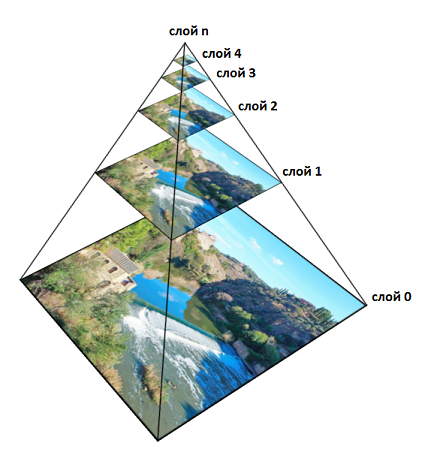
3Dではメモリの総量が等しくなることを計算するのは簡単です どこで -元のボリュームを保存するために必要なメモリの量。 しかし、ピラミッドの使用には、私たちが遭遇した多くの困難と問題があり、それらについて話すと別の記事になります。

まとめ

中心線を構築するための上記のアプローチは非常に効果的であると考えることができますが、いくつかの欠点があります。

1. CT検査では、骨の内側を通る血管（脊椎など）を検出することはできません
2. 血管が細長い細長い骨、組織、または構造の近くを通過する場合、血管を検出できるとは限りません（そのような場合、骨、組織、および構造自体が血管と間違われる可能性があります）
3. ボトルネックは分岐（血管の分岐）です

問題1と2は、骨を差し引くことで解決されます。 このため、2つのCT検査が必要です-コントラストありとコントラストなし。 このような研究の唯一の違いは照明付きの血管であることは明らかです。 言い換えると、血管のある研究の各ボクセルの強度から血管のない研究の各ボクセルの強度を差し引くと、血管に属するボクセルのみが非ゼロ強度になります。 しかし、患者の体のまったく同じ位置で2つの研究を行うことはできないため、主な問題は3D空間での2つの研究の組み合わせです。 これを行うには、回転と変位の変換を使用します。 空間の方向は骨に沿って進むため、 それらは剛体構造です。 骨を見つけるために、グラフに基づくウォーターフォールの非常に興味深いアルゴリズムを使用しました。



分岐の問題は、血管の始点と終点を示すことで解決されます。その間に中心線を構築する必要があります。 2方向のそれぞれの2点のそれぞれで構築を開始する必要があり、中心線を横切るときは、単純にそれらを1つに結合します。 なぜなら 血管は一方向にのみ分岐します（動脈の場合は太い血管が細くなり、静脈の場合は細い血管が太くなります）。このアプローチにより、2つのポイントを接続できます。



それだけです、ご清聴ありがとうございました。 念のため、製品へのリンク 。