background-color: #9B51E0

をこの特定の紫色として認識するのはなぜですか？

長い間、私はこの質問に対する答えを知っていると思っていました。しかし、よく熟考した後、彼は知識に大きなギャップがあることに気づきました。

今、私はこれらのギャップのいくつかを、電磁放射、光学生物学、比色分析、カラーイメージング機器を研究することで埋めることを望んでいます。必要に応じて、特定のセクションにスキップできます。ここに目次があります。

それ以外の場合は、物理学から始めましょう。

電磁放射

電波、マイクロ波、赤外線、可視光、紫外線、X線、ガンマ線はすべて電磁放射の形式です。これらの呼び方は異なりますが、これらの名前は単に電磁スペクトルの異なる波長範囲を示しています。

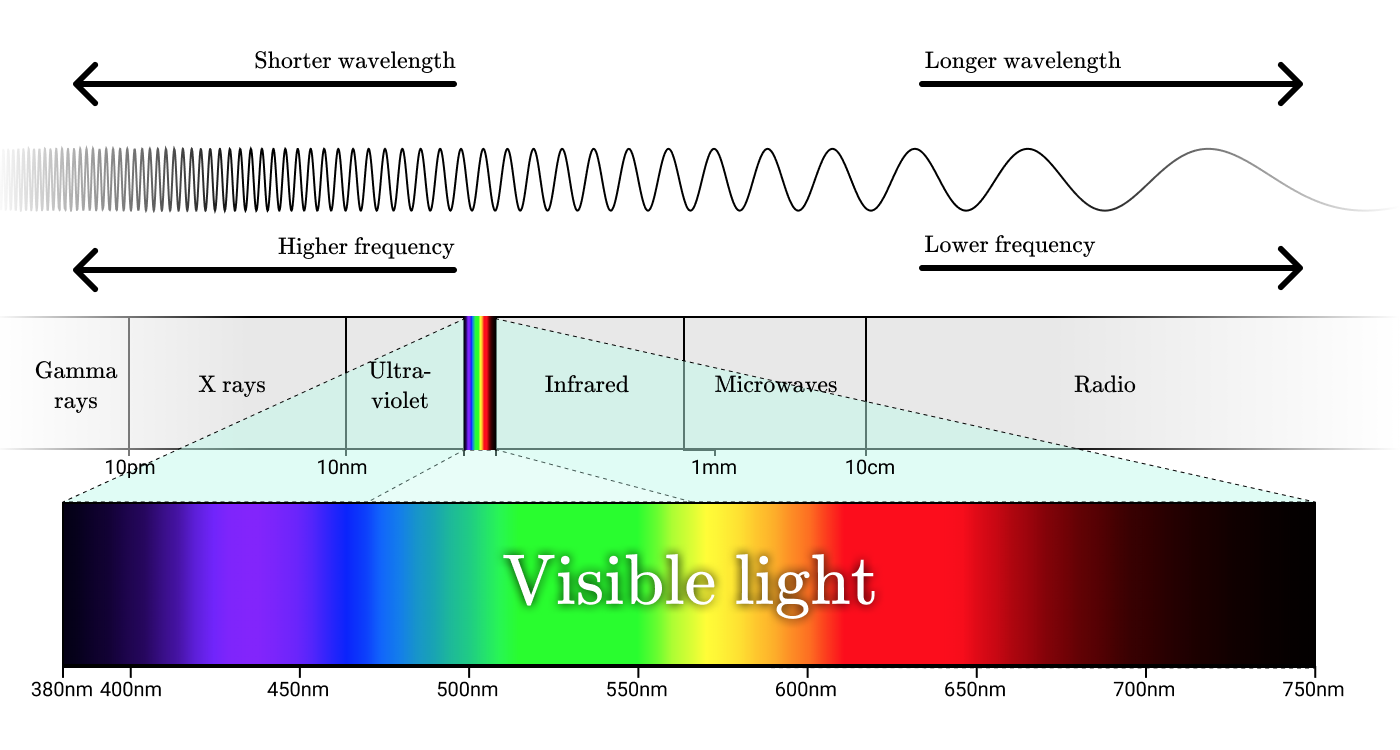
電磁スペクトル

電磁放射の最小単位は光子です。光子のエネルギーは対応する波の周波数に比例し、高エネルギーの光子は高周波に対応します。

色を理解するには、まず放射線を理解する必要があります。白熱灯の放射を詳しく見てみましょう。

写真：アレックス・アイビー

ランプがどれだけのエネルギーを放出するかを尋ねることができます。 放射束 （

P h i_{e}

$\ Phi_e$ ）オブジェクトとは、1秒あたりに放出される総エネルギーであり、ワットで測定されます。 100ワットの白熱電球の放射束は約80ワットで、残りの20ワットは非放射熱に直接変換されます。

各波長範囲にどれだけのエネルギーが含まれるかを知りたい場合は、放射のスペクトル密度を調べることができます。スペクトル放射密度（

P h i_{e 、 l a m b d a}

$\ Phi_ {e、\ lambda}$ ）は、単位波長あたりの放射束です。通常、ワット/ナノメートルで測定されます。

白熱電球のスペクトル放射密度を波長の関数として表すと、次のようになります。

この曲線で囲まれた領域は、放射束に対応します。方程式の形で：

P h i_{e} = i n t_{0}^{} i n f t y P h i_{e 、 l a m b d a} （ l a m b d a ） d l a m b d a

$\ Phi_e = \ int_0 ^ \ infty \ Phi_ {e、\ lambda}（\ lambda）d \ lambda$ 。この場合、領域の面積は約80ワットに相当します。

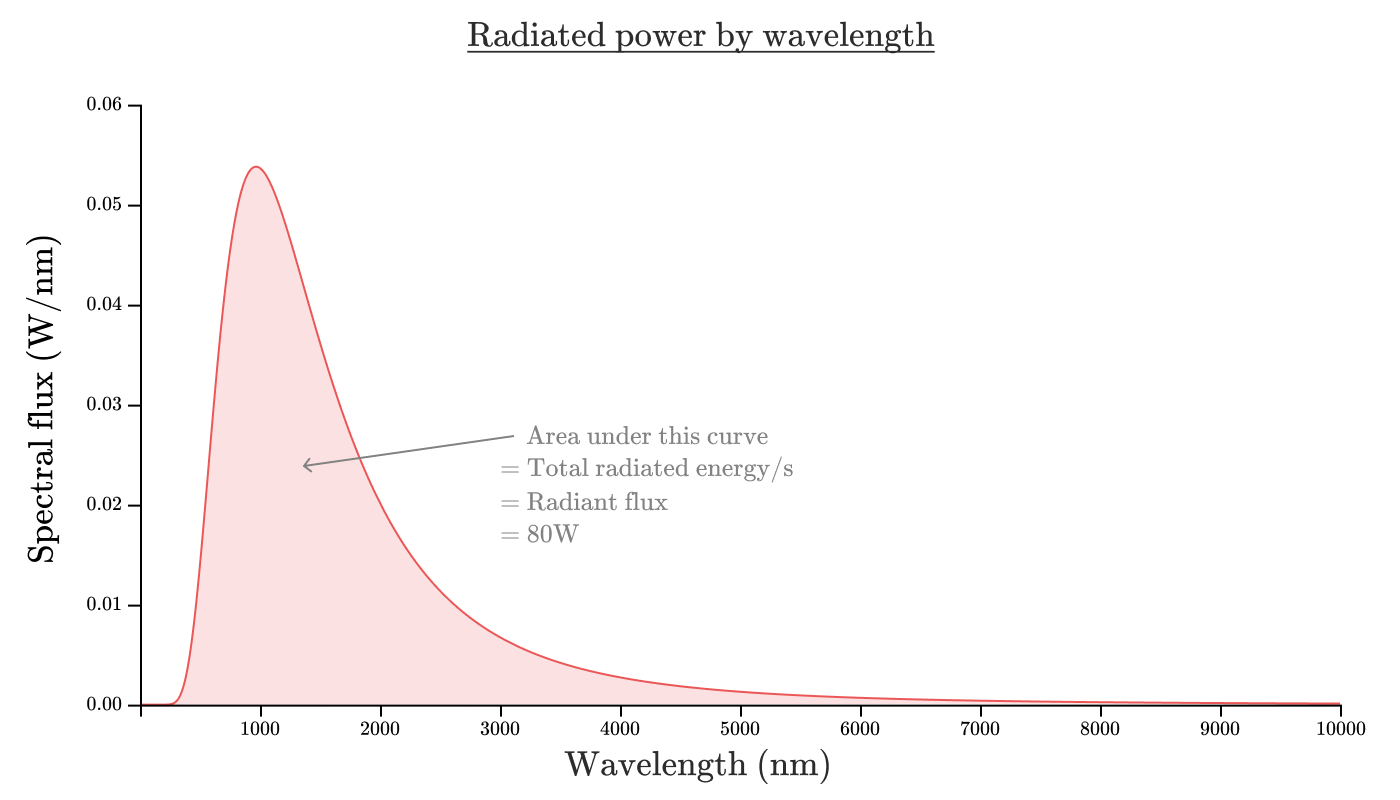
P h i_{e}^{t e x t b u l b} = i n t_{0}^{} i n f t y P h i_{e 、 l a m b d a}^{} t e x t b u l b （ l a m b d a ） d l a m b d a = 80 t e x t W

$\ Phi_ {e} ^ {\ text {bulb}} = \ int_0 ^ \ infty \ Phi_ {e、\ lambda} ^ \ text {bulb}（\ lambda）d \ lambda = 80 \ text {W}$

環境保護主義者の広告から、白熱電球は非常に効果がないと聞いたことがあります。「うーん、80％はそれほど効率が悪いとは思わない」

そして、それは本当です。白熱電球は、電気を放射線に変換する非常に効果的な方法です。残念ながら、これは電気を人間の目に見える放射線に変換するひどい方法です。

可視光

可視光の波長範囲は

l a m b d a = 380 t e x t n m

$\ lambda = 380 \ text {nm}$ 前に

l a m b d a = 750 t e x t n m

$\ lambda = 750 \ text {nm}$ 。白熱灯のグラフでは、これは下図の影付きの領域です。

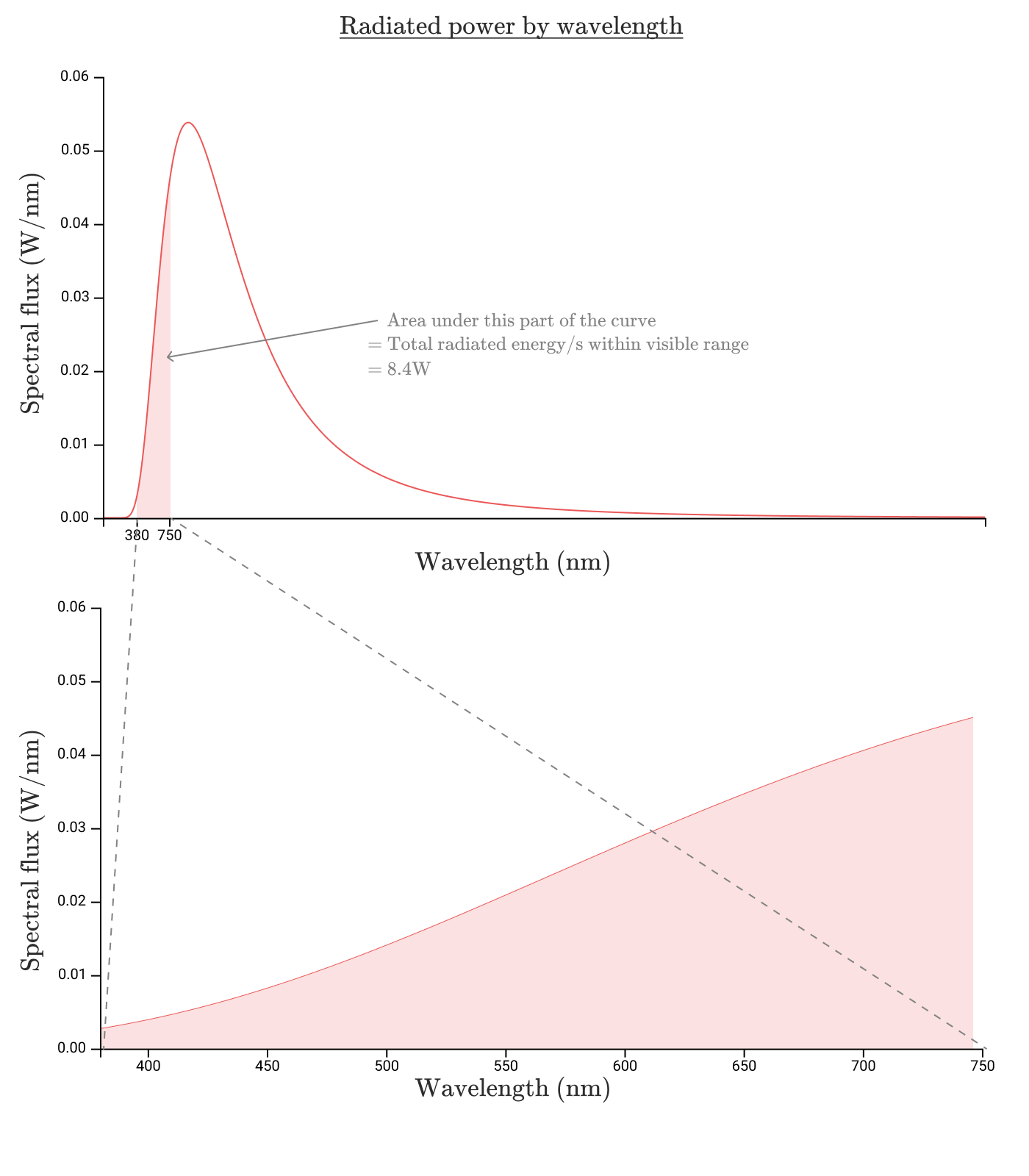
i n t_{380 t e x t n m}^{750 t e x t n m} P h i_{e 、 l a m b d a}^{} t e x t b u l b （ l a m b d a ） d l a m b d a = 8.7 W

$\ int_ {380 \ text {nm}} ^ {750 \ text {nm}} \ Phi_ {e、\ lambda} ^ \ text {bulb}（\ lambda）d \ lambda = 8.7W$

したがって、 可視範囲では8.7 Wが放出され、8.7％の効率が得られます。ひどいですね。実際、状況はさらに悪化しています。

理由を理解するために、可視光が見える理由を見てみましょう。

知覚可能な明るさ

写真提供：クリストファー・バーンズ

白熱灯がすべての波長で等しく発光しないのと同じように、私たちの目もすべての範囲の放射線に等しく敏感ではありません。各波長に対する人間の目の感度を測定すると、単色放射の相対的なスペクトル光効率の関数が得られます。標準スペクトル発光効率関数

b a r y （ \ラ ム ダ ）

$\ bar y（\ラムダ）$ 次のようになります。

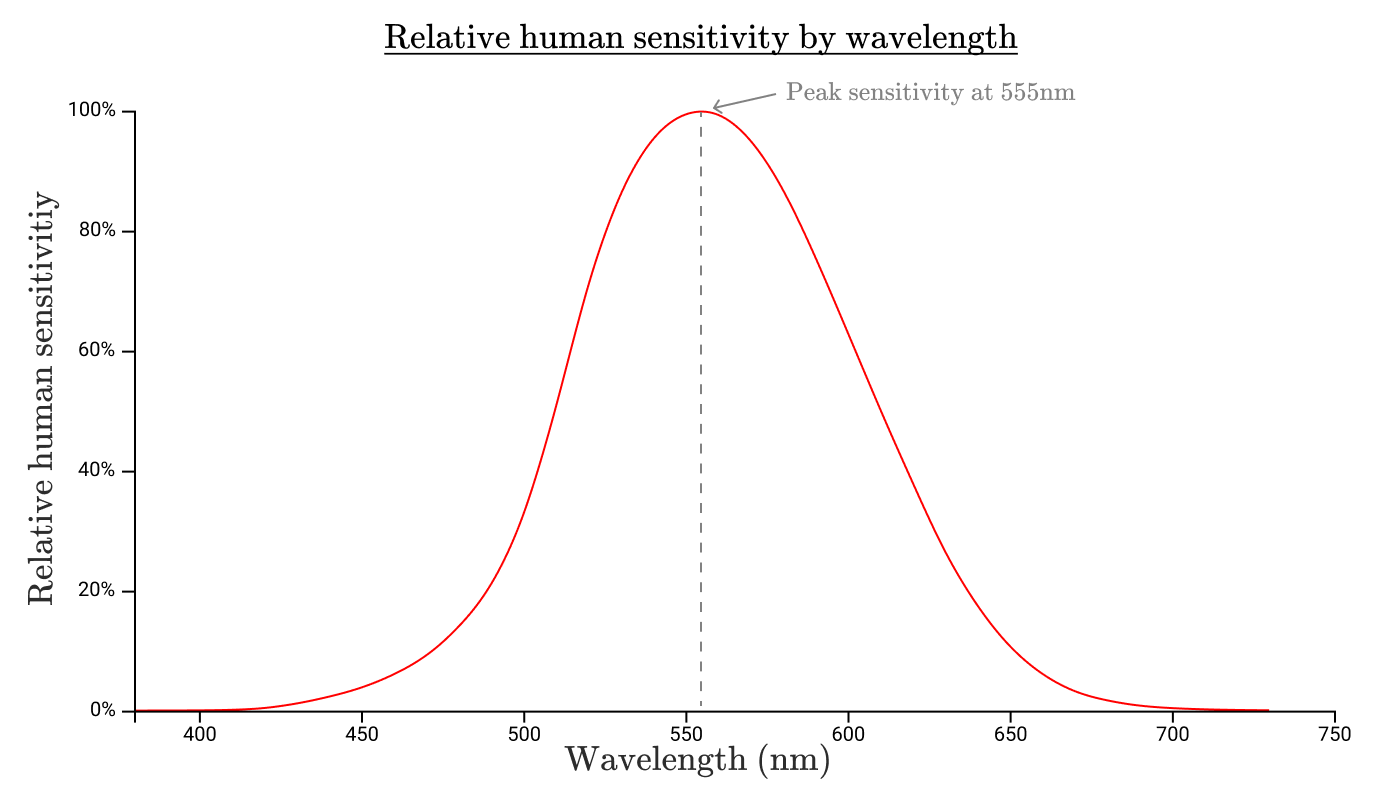
この関数の境界は、可視光の範囲を決定します。私たちの目はこの光を知覚しないので、この範囲外には何も見えません！

この曲線は、私たちの目が650 nmまたは450 nmの放射よりも550 nmの放射にはるかに敏感であることも示しています。

他の動物の目は他の範囲の波に敏感であり、したがって、相対的なスペクトル光効率の他の機能がそれらに作用します。鳥は、紫外線範囲の放射線を見ることができます

l a m b d a = 300 t e x t n m

$\ lambda = 300 \ text {nm}$ 前に

l a m b d a = 400 t e x t n m

$\ lambda = 400 \ text {nm}$ したがって、科学的な鳥が電磁スペクトルに関する科学記事を書いた場合、範囲のこの部分を「可視光」と呼びます。

写真：ティモシー・ライン

放射のスペクトル密度のプロットに単色放射の相対スペクトル光効率の関数を掛ける

b a r y （ \ラ ム ダ ）

$\ bar y（\ラムダ）$ 、光源から放射される各波長の、人間が知覚する明るさへの寄与を記述する関数を取得します。

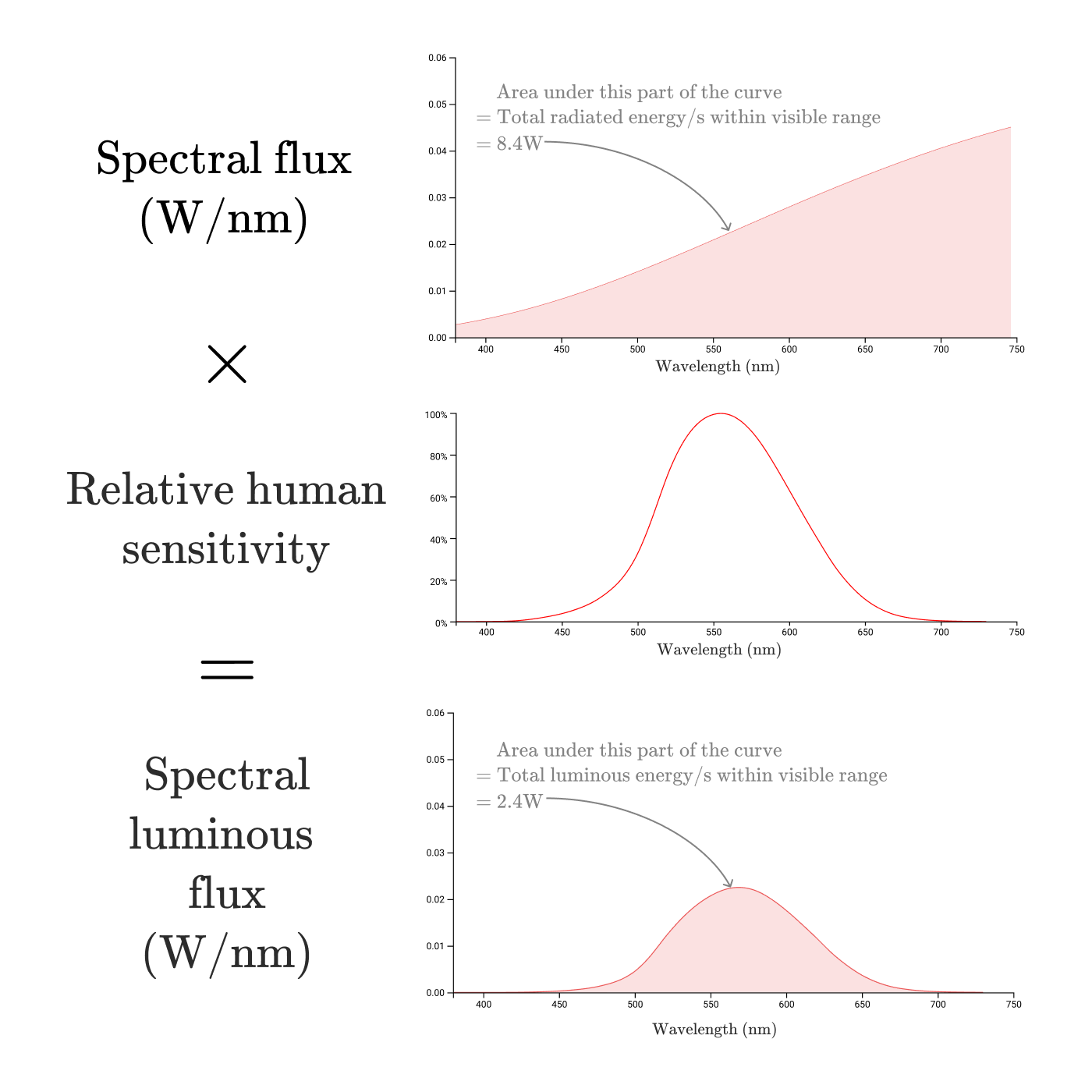
これは、 光束のスペクトル密度 （

P h i_{v 、 l a m b d a}

$\ Phi_ {v、\ lambda}$ ）客観的な出力ではなく人間の知覚との関係を強調するために、光束はワットではなくルーメンで測定され、変換係数は683.002 lm / Wです。

P h i_{v 、 l a m b d a} （ l a m b d a ） = 683.002 f r a c t e x t l m t e x t W c d o t b a r y （ l a m b d a ） c d o t P h i_{e 、 l a m b d a} （ \ラ ム ダ ）

$\ Phi_ {v、\ lambda}（\ lambda）= 683.002 \ frac {\ text {lm}} {\ text {W}} \ cdot \ bar y（\ lambda）\ cdot \ Phi_ {e、\ lambda} （\ラムダ）$

光束（

P h i_{v}

$\ Phi_v$ ）光源から-これは、 人が知覚する総光パワーです。

放射束の曲線で囲まれた領域の面積を計算して放射束を計算したように、光束のスペクトル密度曲線で囲まれた領域を取得して、知覚される放射のワットからルーメンへの変換で光束を見つけることができます：

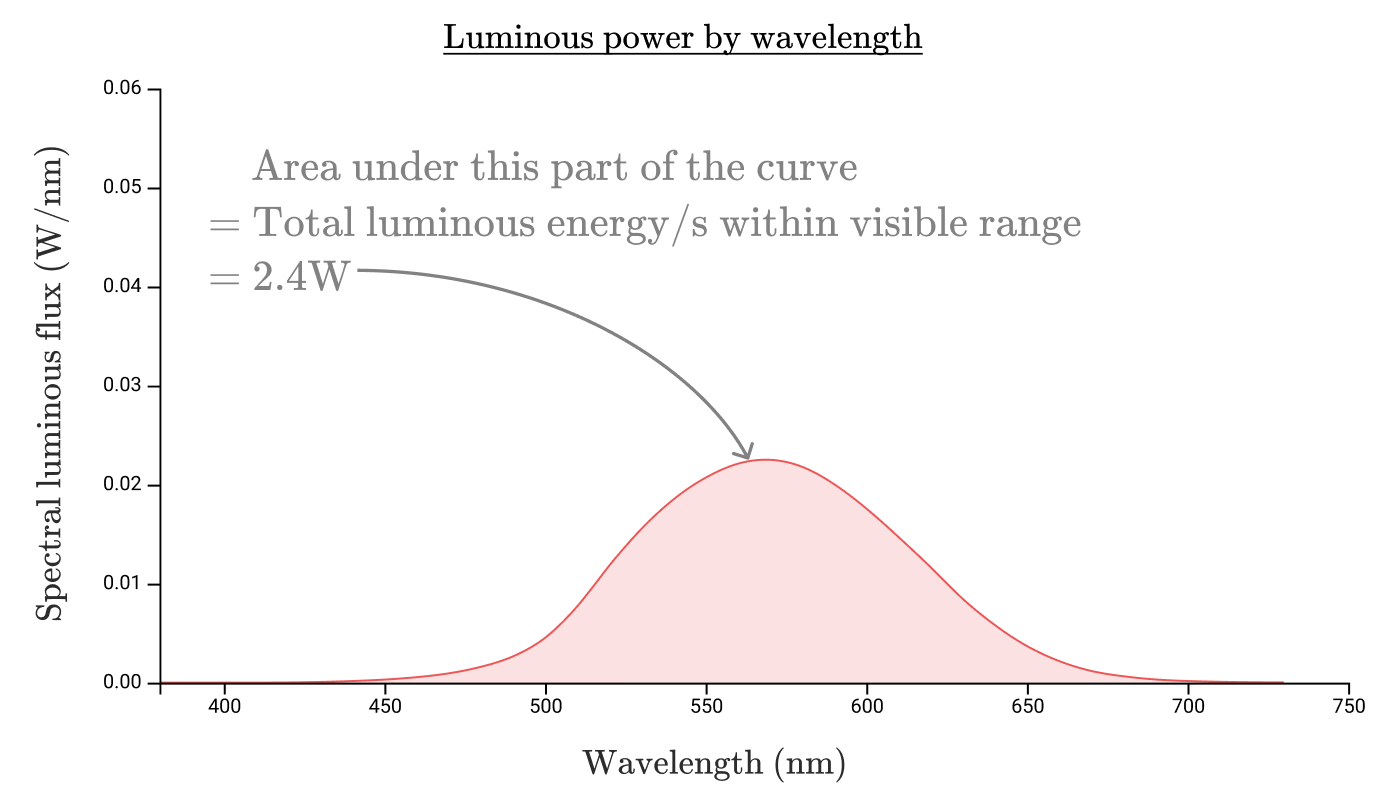
P h i_{v}^{} t e x t b u l b = i n t_{0}^{} i n f t y b a r y （ l a m b d a ） c d o t P h i_{e 、 l a m b d a}^{} t e x t b u l b （ l a m b d a ） d l a m b d a = 683.002 f r a c t e x t l m t e x t W c d o t 2.4 t e x t W \約 1600 t e x t l m

$\ Phi_ {v} ^ \ text {bulb} = \ int_0 ^ \ infty \ bar y（\ lambda）\ cdot \ Phi_ {e、\ lambda} ^ \ text {bulb}（\ lambda）d \ lambda = 683.002 \ frac {\ text {lm}} {\ text {W}} \ cdot 2.4 \ text {W} \約1600 \ text {lm}$

したがって、当社の100ワット白熱灯の光束は、悲惨な2.4 Wまたは1600ルーメンです！白熱灯の発光効率はわずか2.4％であり、電気の放射への80％変換の効率とはかけ離れています。

おそらく、光源が放射を可視範囲に集中させた場合、より効率的な照明を得ることができます。白熱灯、蛍光灯、LEDランプのスペクトルを比較してみましょう。

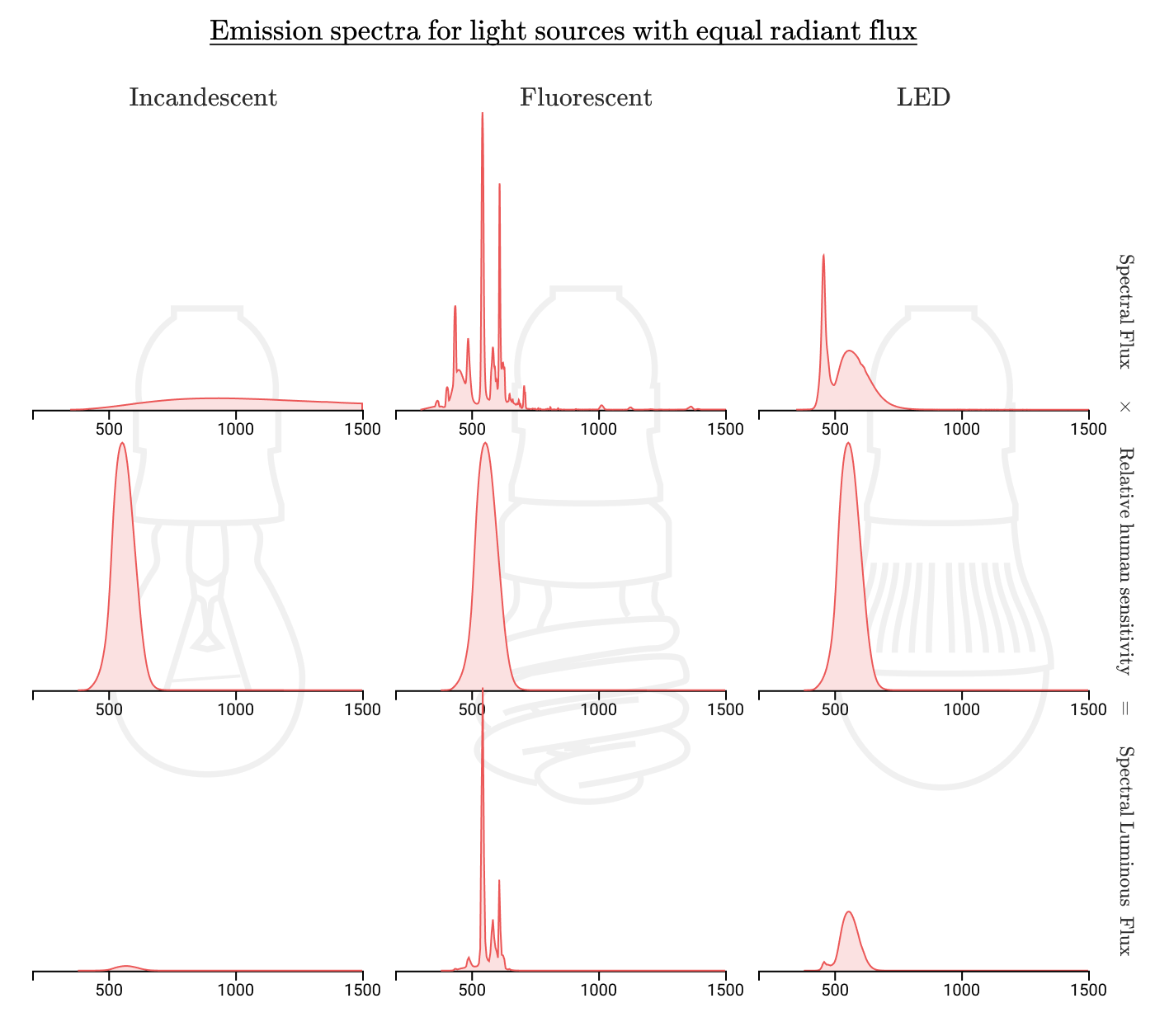
実際、蛍光灯とLEDランプは、人間には見えない範囲ではるかに少ないエネルギーを消費します。白熱灯の効率が1〜3％の場合、蛍光灯の場合は約10％、LEDランプの場合は最大20％です。

しかし、記事のトピックに戻って、十分な明るさ：色！

色の定量化

写真：ローレン・マンケ

この色を識別する方法は？目の前にレモンがある場合、電話でどのような色を言うことができますか？レモンは黄色だと言えますが、どれが黄色ですか？これらの黄色の各色を正確に識別する方法は？

色は電磁放射の人間による解釈であるという知識を武器に、放射のスペクトル密度を使用して数学的に色を決定するのは魅力的かもしれません。人が見る色は、単色（単一波長）の一種のバランスのとれた組み合わせになります。単色は、スペクトル色とも呼ばれます。

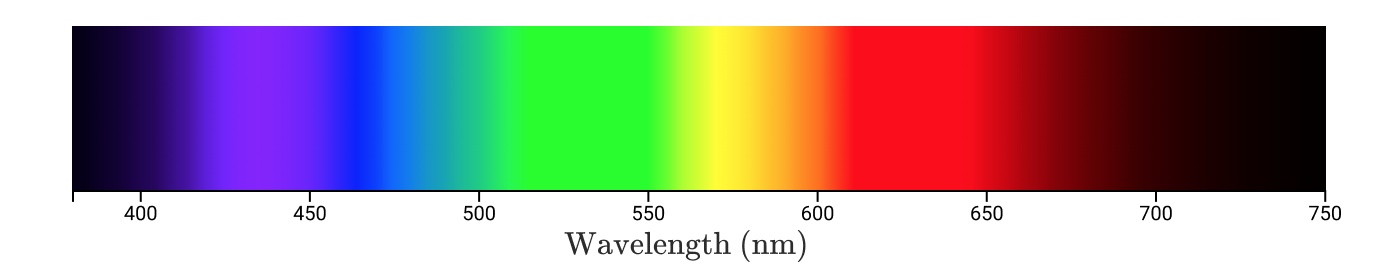
単波長の色

任意のオブジェクトについて、放射（または反射）のスペクトルを測定し、それを使用して色を正確に決定できます。スペクトルを再現できる場合は、色を正確に再現します！

レモン上の点から反射された太陽光は、おおよそ次の反射スペクトルを持つ可能性があります。

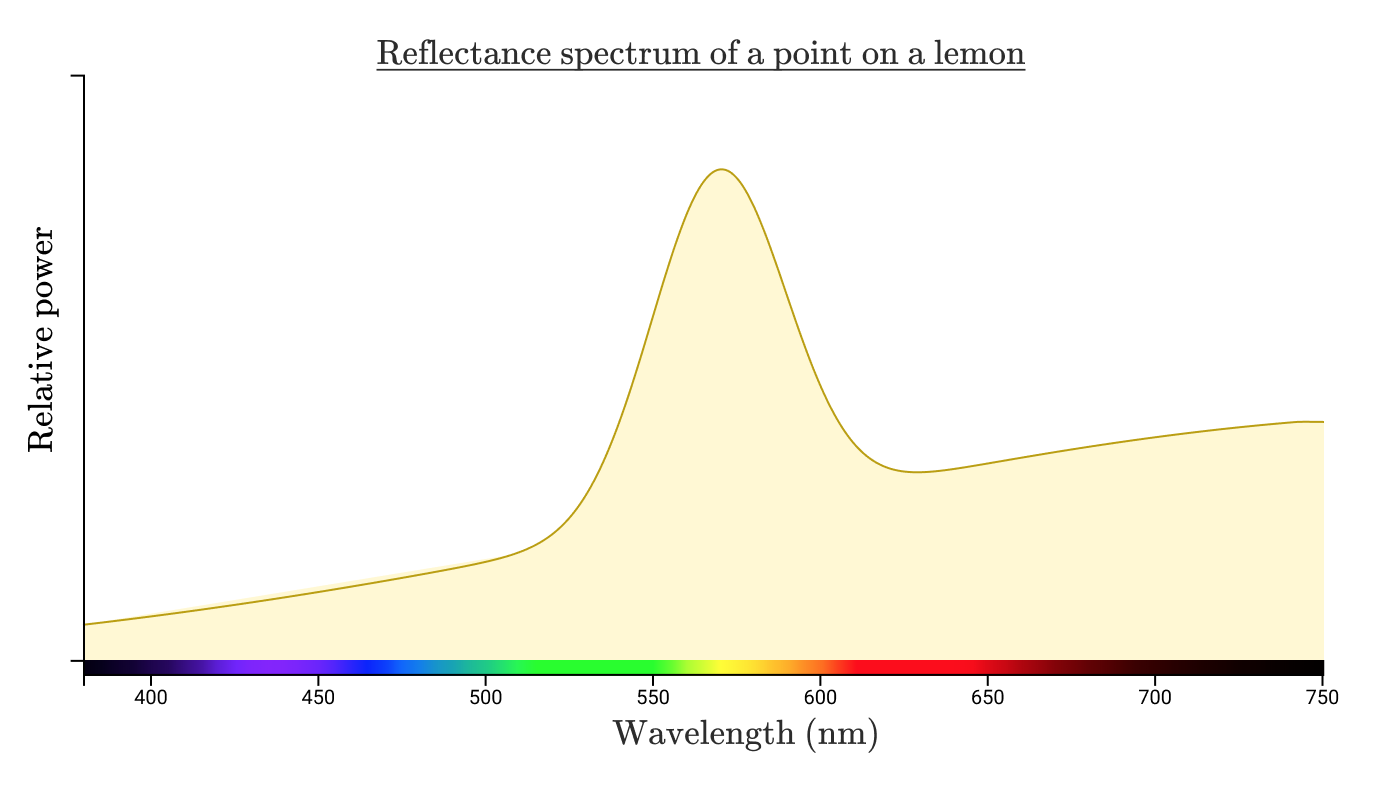
注：目に到達する放射線のパワーと強度の分布は、光源のパワーと発光スペクトル、光源から照らされたオブジェクトまでの距離、オブジェクトのサイズと形状、オブジェクトの吸収スペクトル、およびユーザーからオブジェクトまでの距離に依存します。 考えることがたくさんありますので、この光が人間の目に届くときに何が起こるかに焦点を当てましょう。 今のところ、ユニットを無視して、概念に焦点を合わせます。

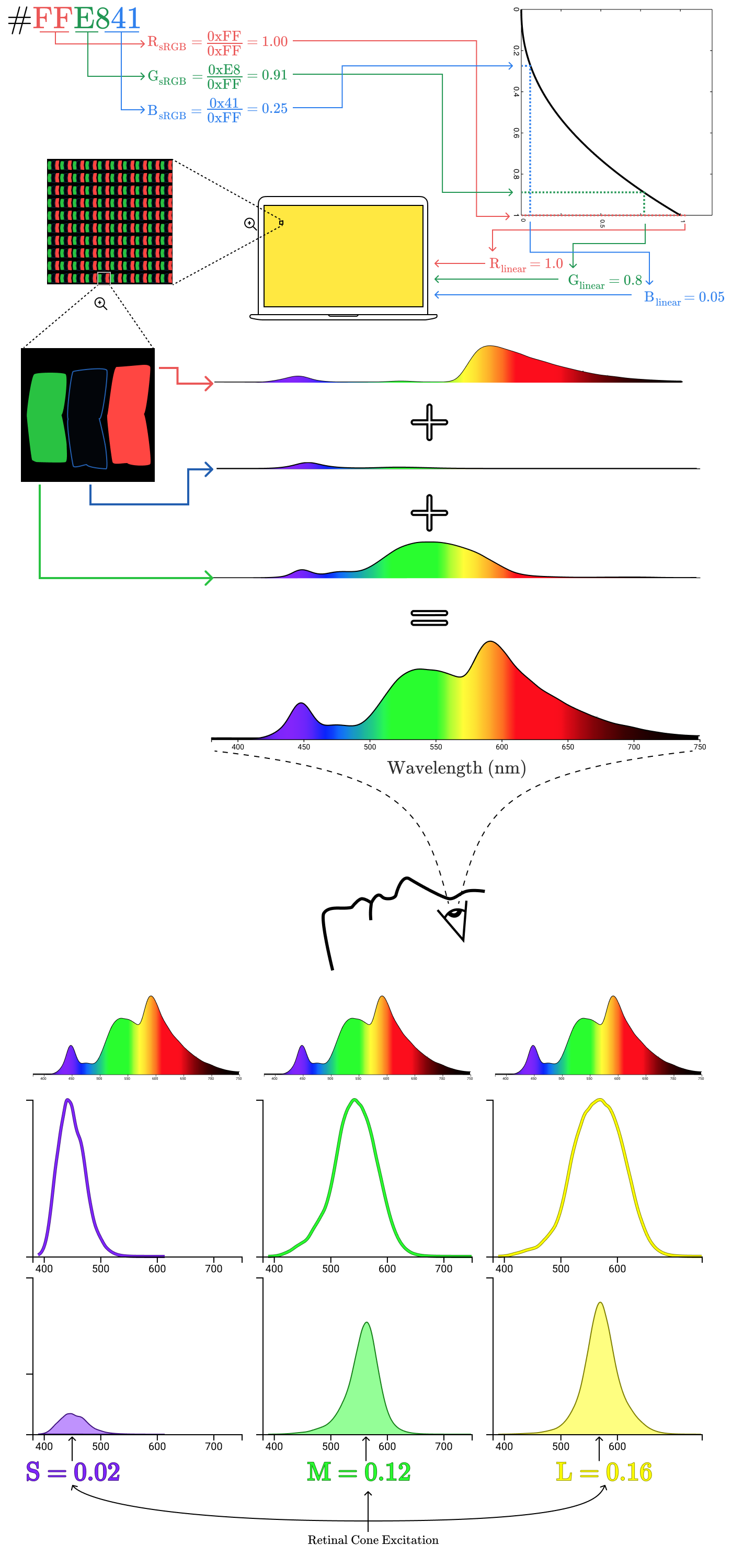
このようなスペクトル分布のエネルギーが人間の目に入ると、彼はそれを「黄色」と知覚します。レモンの写真を撮って、その写真をコンピューターにアップロードしたとします。次に、画面上のレモンの特定のポイントが実際の手の実際のレモンの色と変わらないように、画面上の色を慎重に調整しました。

画面からスペクトル強度分布を測定する場合、どのように見えると思いますか？上記のレモンの反射スペクトルに似ていることを期待するのは合理的です。しかし、実際には次のようになります。

人間の観察者にとって同じように見える2つの異なるスペクトル強度分布は、 メタマーと呼ばれます。

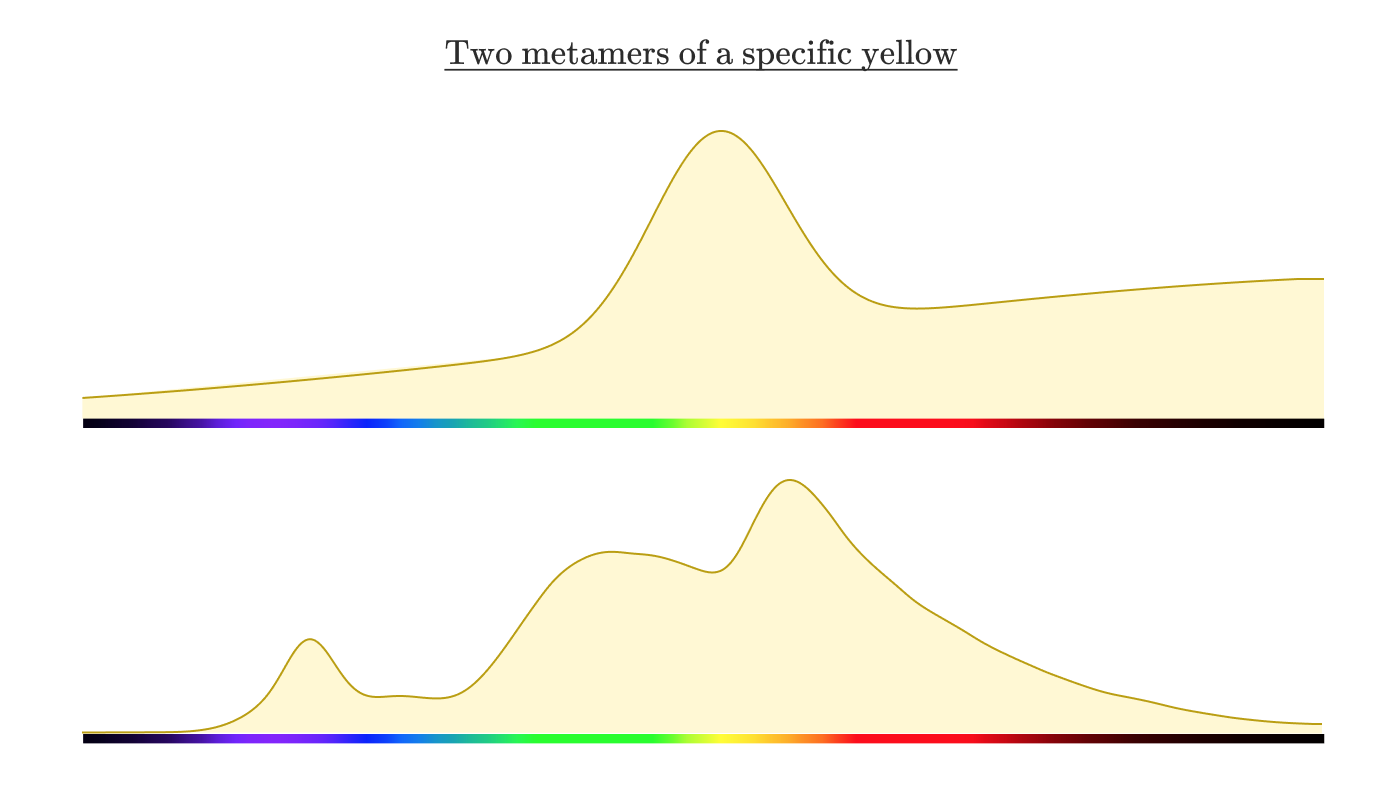
これがどのように可能であるかを理解するには、目の生物学を考慮してください。

光生物学

写真：アマンダ・ダルビョルン

目の網膜、rod体、および錐体の特殊な細胞は、光の知覚に関与しています。スティックは主に低光条件で重要であり、色の知覚に大きな役割を果たさないため、コーンに焦点を当てます。

人々は通常、3種類のコーンを持っています。 3つの異なるタイプのコーンが存在するため、人は「三色覚」になります。ただし、ヒトテトラクロマチンの症例が少なくとも1つ確認されています！他の動物にはさらに多くのコーン種があります。脚足類には 16種があります。

各タイプのコーンは、反応する光の波長によって示されます。標準指定は、S、M、およびL（短波、中波、長波）です。

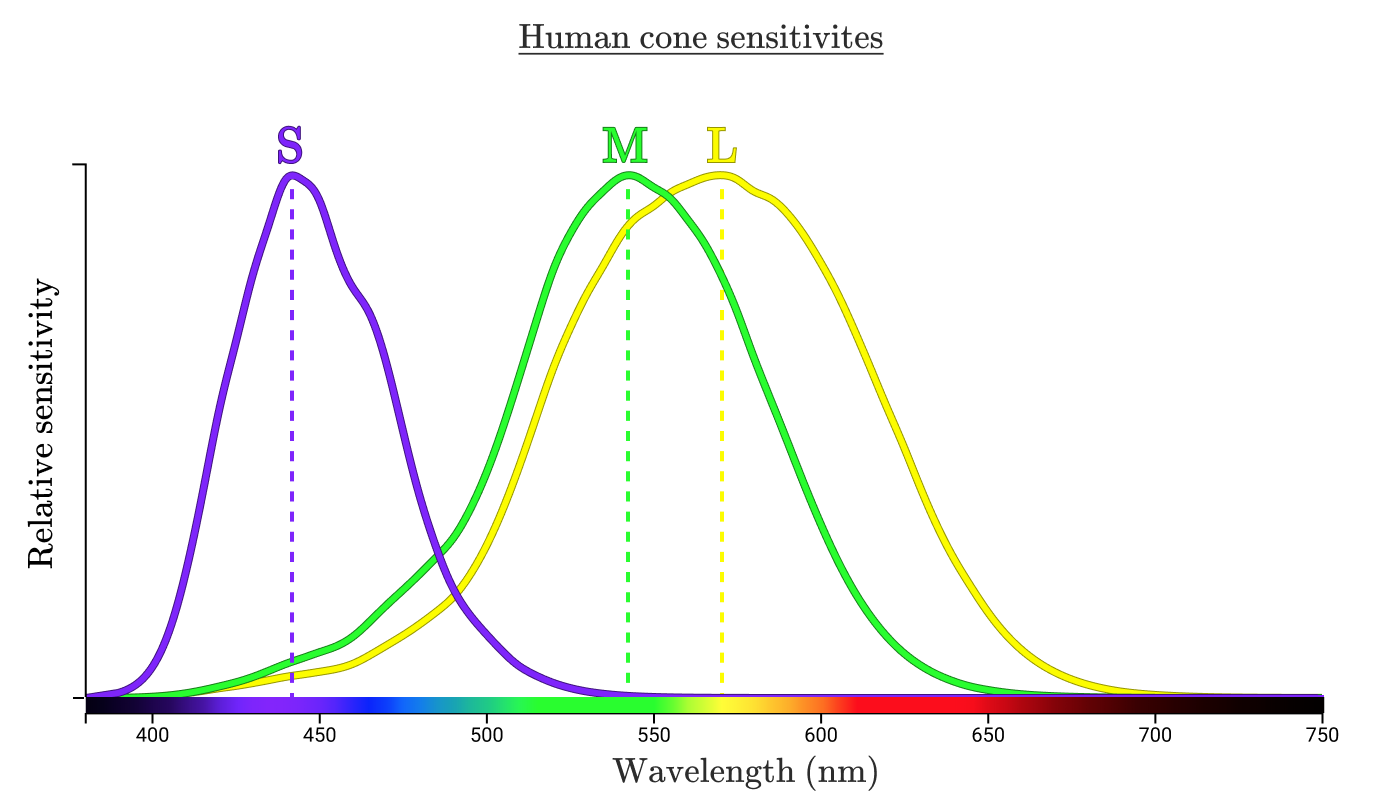
3つの曲線は、特定のタイプのコーンが各波長に対してどの程度敏感かを示しています。各曲線の最高点は「ピーク波長」と呼ばれ、コーンが最も敏感な波長を示します。

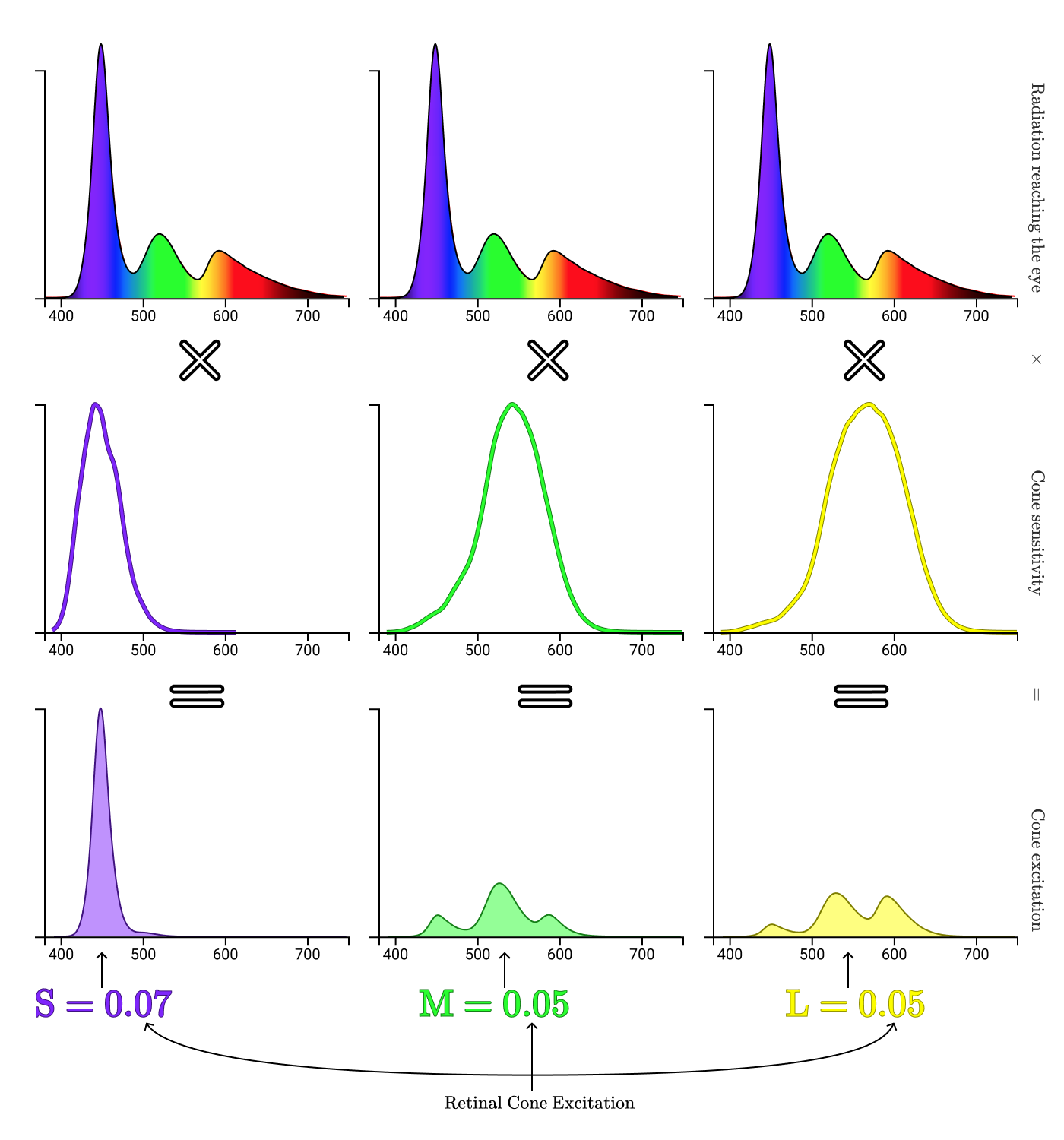
手のレモンからの反射光をコーンがどのように処理するかを見てみましょう。

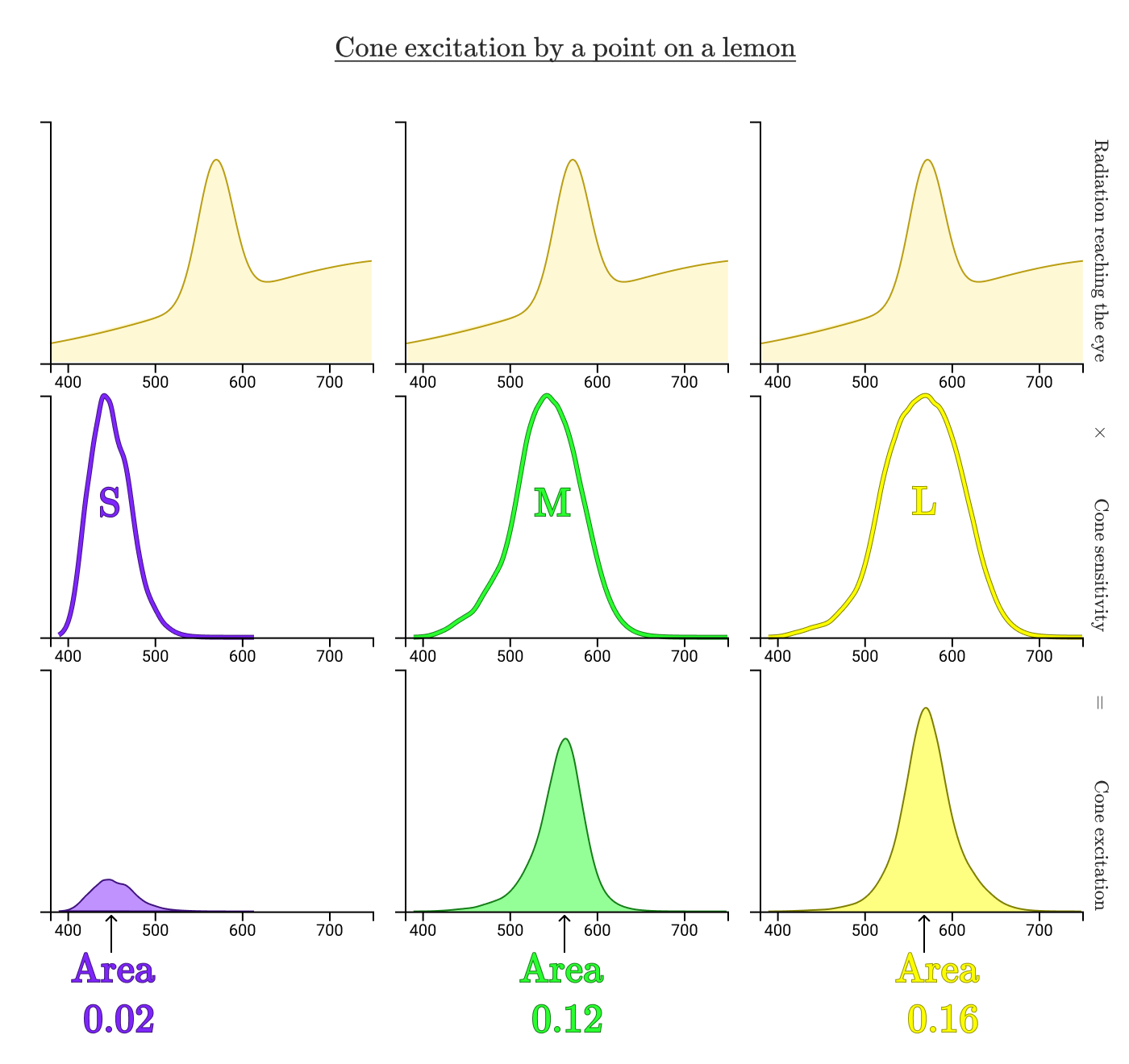
曲線で囲まれた領域は、レモンから反射された放射のどの程度が各タイプのコーンを励起するかを示しています。この場合、円錐S、M、およびLの正規化された励起は、それぞれ0.02、0.12、および0.16です。次に、画面上のレモンのプロセスを繰り返します。

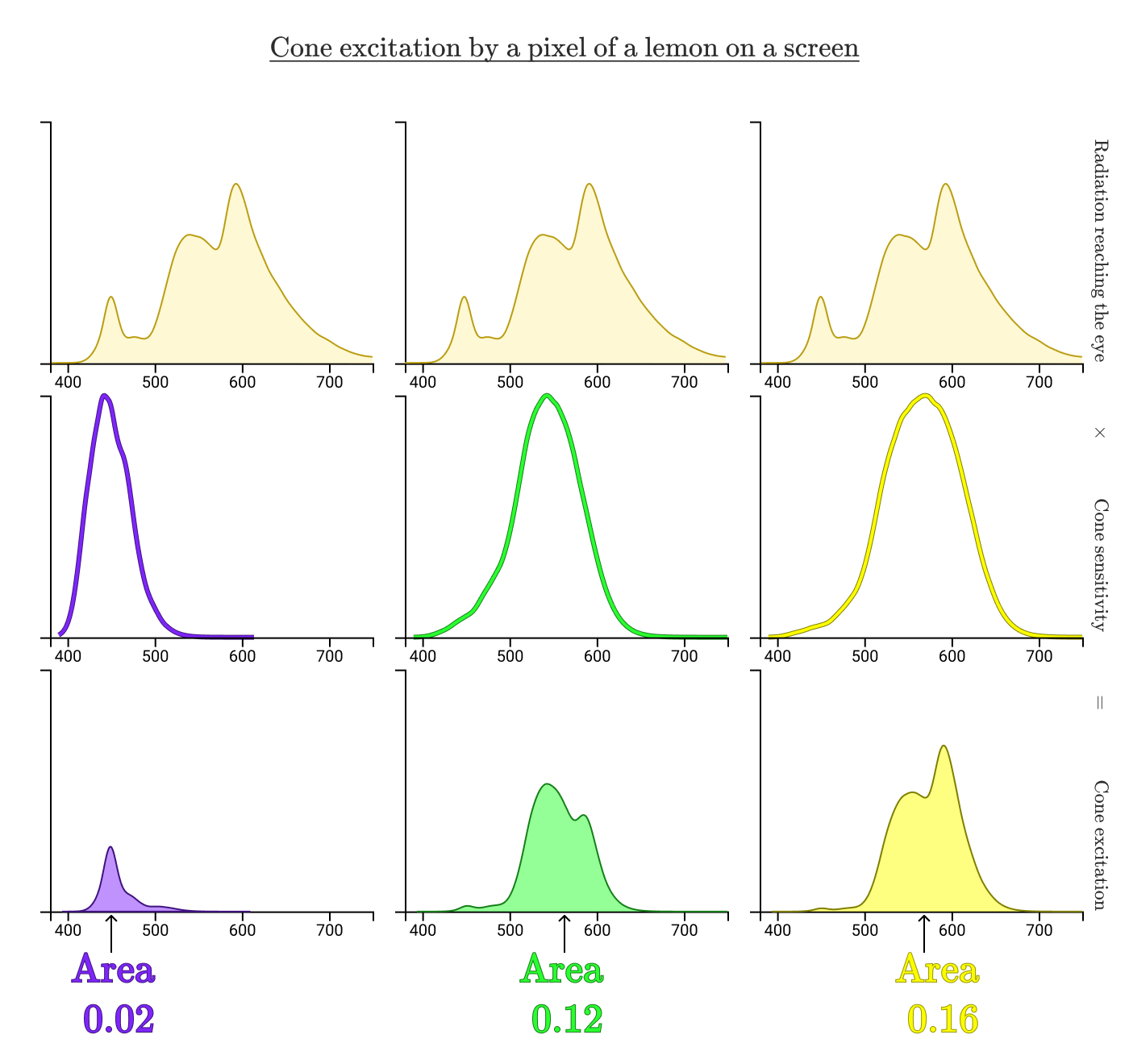
放射スペクトルは完全に異なりますが、コーンの励起は同じです（S = 0.02、M = 0.12、L = 0.16）。それが、本物のレモンのドットとデジタルレモンのドットが同じように見える理由です！

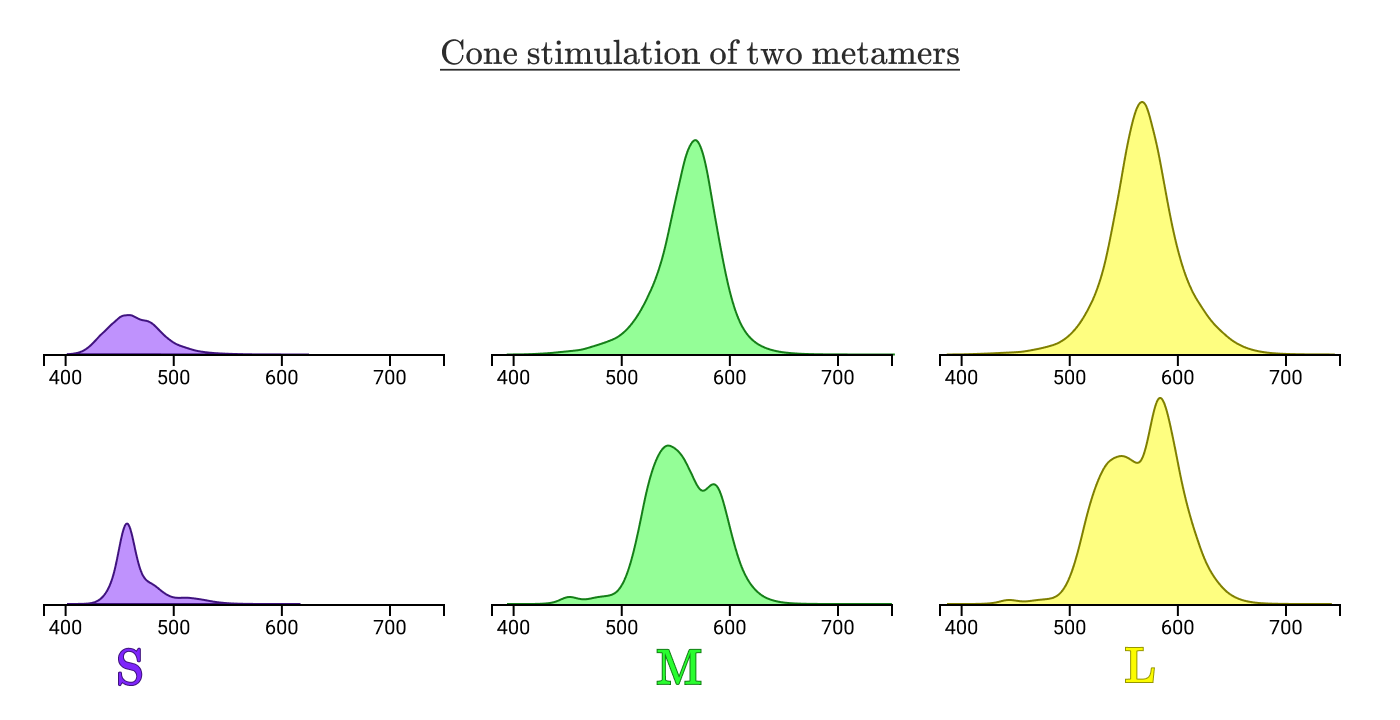
メタマーは常に、3種類のコーンの刺激曲線の下に正規化された領域を持ちます。

3つのコーンセットは、スペクトルフラックス密度曲線を低減します。

P h i_{e} （ \ラ ム ダ ）

$\ Phi_e（\ラムダ）$ トリプルの数へ

（ S 、 M 、 L ）

$（S、M、L）$ 、および個別のトリプレット

（ S 、 M 、 L ）

$（S、M、L）$ 別の色になります！複雑な連続関数を使用するよりも個々の数字（0.02、0.12、0.16）を使用する方がはるかに簡単なので、これは非常に便利です。数学愛好家の場合：私たちの目は、無限次元の空間から3次元への次元縮小を実行します。これを無意識に行うことができるのはとてもクールです。

現実のトリプレット

（ S 、 M 、 L ）

$（S、M、L）$ -これは、色空間の最初の例です。

色空間

色空間を使用すると、色を定量化できます。前の章で、特定の黄色がSML色空間で（0.02、0.12、0.16）として表されることを確認しました。これは、 LMS色空間として知られています。

この色空間は錐体の刺激を表すため、定義上、人の目に見える色はすべて正のLMS座標で表すことができます（3つではなく4つの座標を必要とする非常にまれな四色彩色の人を除く）。

残念ながら、この色空間にはいくつかの役に立たない特性があります。

まず、すべてのトリプレット値（色成分または色座標とも呼ばれる）が物理的に可能なわけではありません。たとえば、LMS座標（0、1、0）。この座標に到達するには、コーンLとSをまったく刺激せずに、コーンMを何らかの方法で刺激する必要がありますが、これは不可能です。

Mコーンを刺激する波長は、タイプLまたはS（またはその両方）のコーンも刺激します。

その結果、たった1種類のコーンの刺激を増やすことは本当に難しいという問題が生じます。この副作用のため、特に、このカラーモデルはディスプレイの生産とあまり互換性がありません。

もう1つの歴史的で実際的な問題は、コーンの正確な感度は1990年代まで知られていなかったことであり、数学的に正確なカラーモデルを開発する必要性はずっと早く生じました。この分野における最初の重要な進歩は1920年代後半に起こりました。

ライトおよびギルドカラー実験

1920年代後半、ウィリアムデビッドライトとジョンギルドは実験を行いました。 3つの特定の波長の寄与により、個々の色を正確に識別しました。

おそらく網膜上の3種類の錐体については知らなかったが、目に見えるすべての色を3色の組み合わせとして表現できるという考えに至る100年前に。

チャールズ・ヘイターの3色カラー理論の例、1826

ライトとギルドは、被験者がテスト波長を固定波長の3つの光源の組み合わせとして決定できるようにする装置を構築するというアイデアを思いつきました。インストールは次のようになりました。

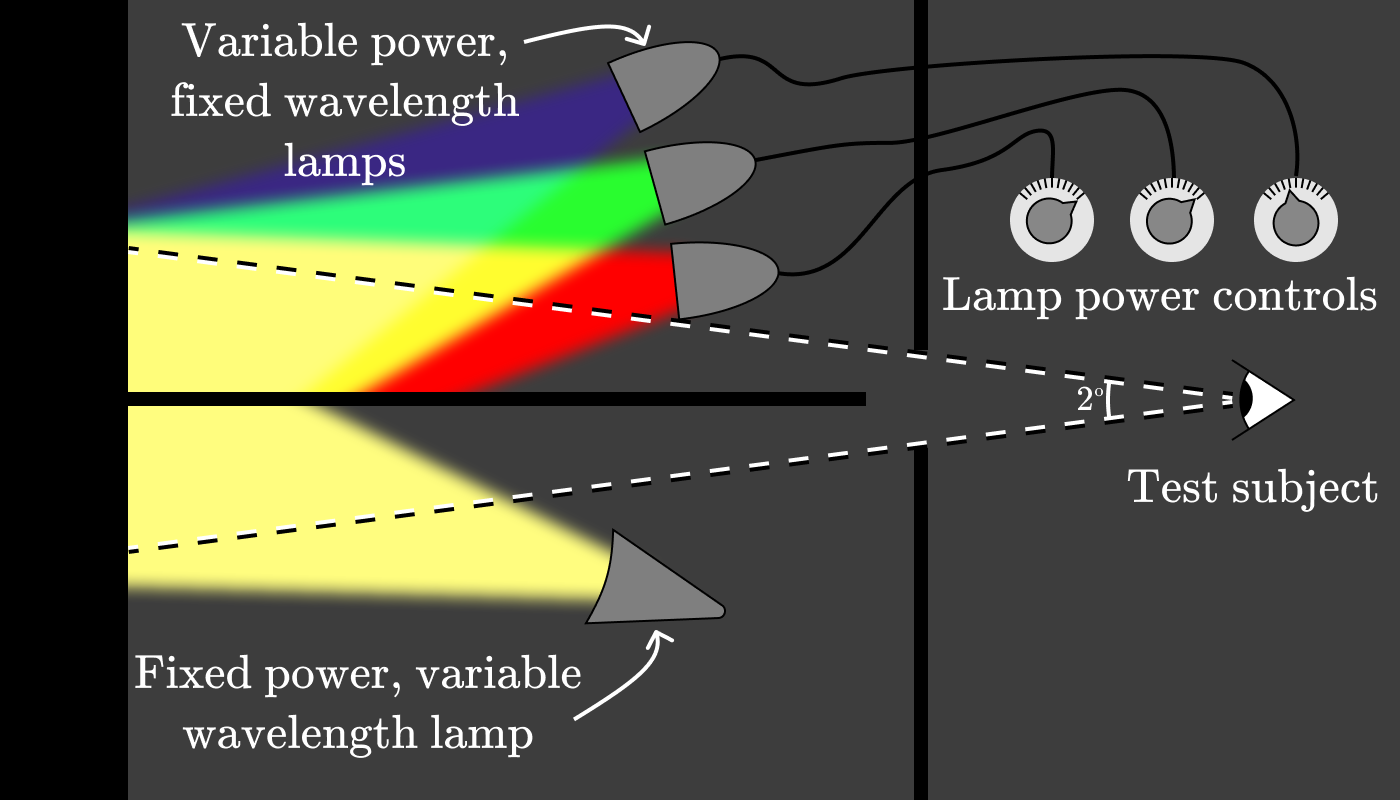
実験者は、以下のランプを特定の波長（たとえば、600 nm）に調整し、色が一致するように3つの制御ランプの出力を調整するように被験者に依頼しました。

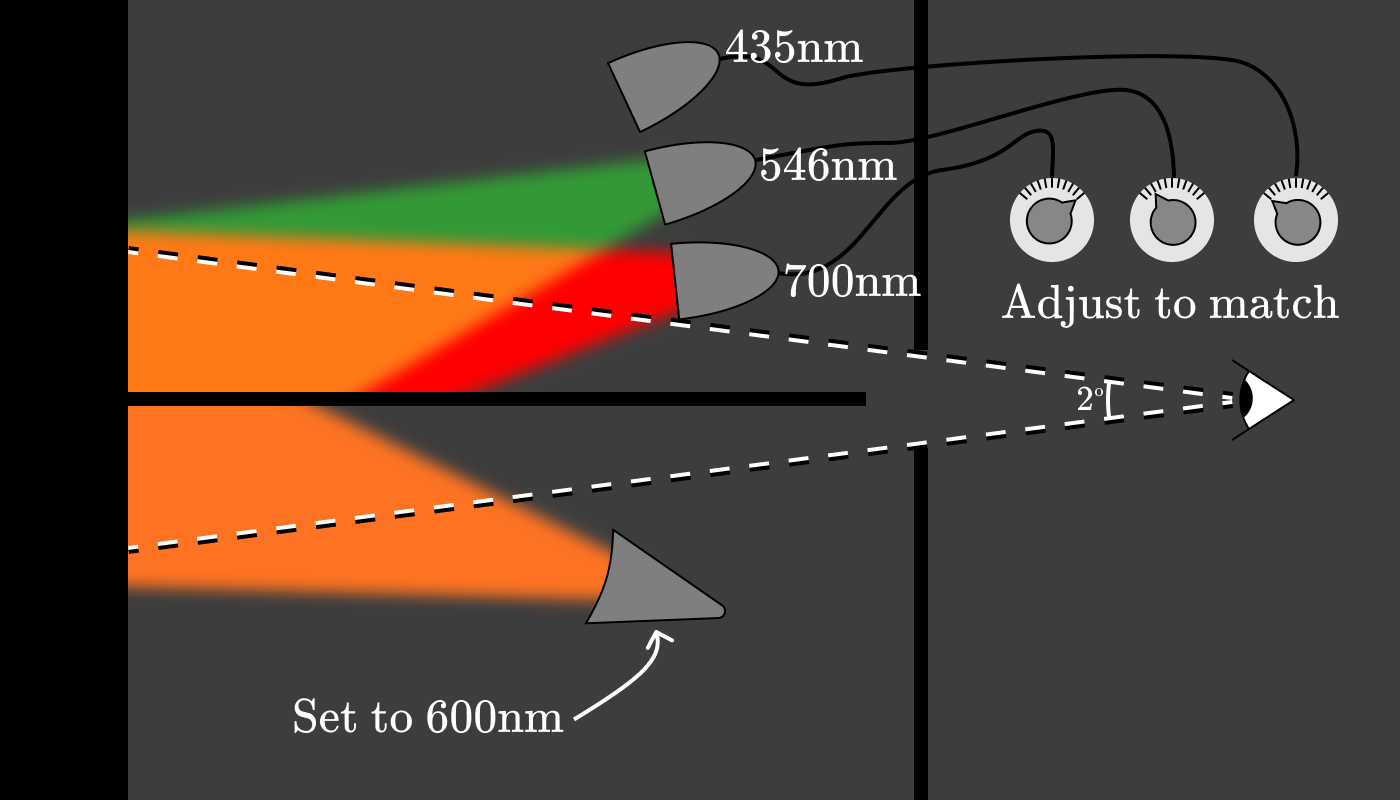
3つのランプ（赤、緑、青）のそれぞれのパワーは、600 nmに相当する3つの純粋なスペクトル色を提供します。約10人の被験者について5 nmごとにこの実験を繰り返した後、特定の波長で色の外観を復元するために必要な赤（700 nm）、緑（546 nm）、青（435 nm）の光の量を示すグラフが作成されました。関数は、 カラーマッチング関数（CMF）として知られています。

これらの特定の色追加機能は次のように知られています

b a r r （ l a m b d a ）

$\ bar r（\ lambda）$ 、

b a r g （ \ラ ム ダ ）

$\ bar g（\ラムダ）$ そして

\バ ー b （ \ラ ム ダ ）

$\バーb（\ラムダ）$ 。

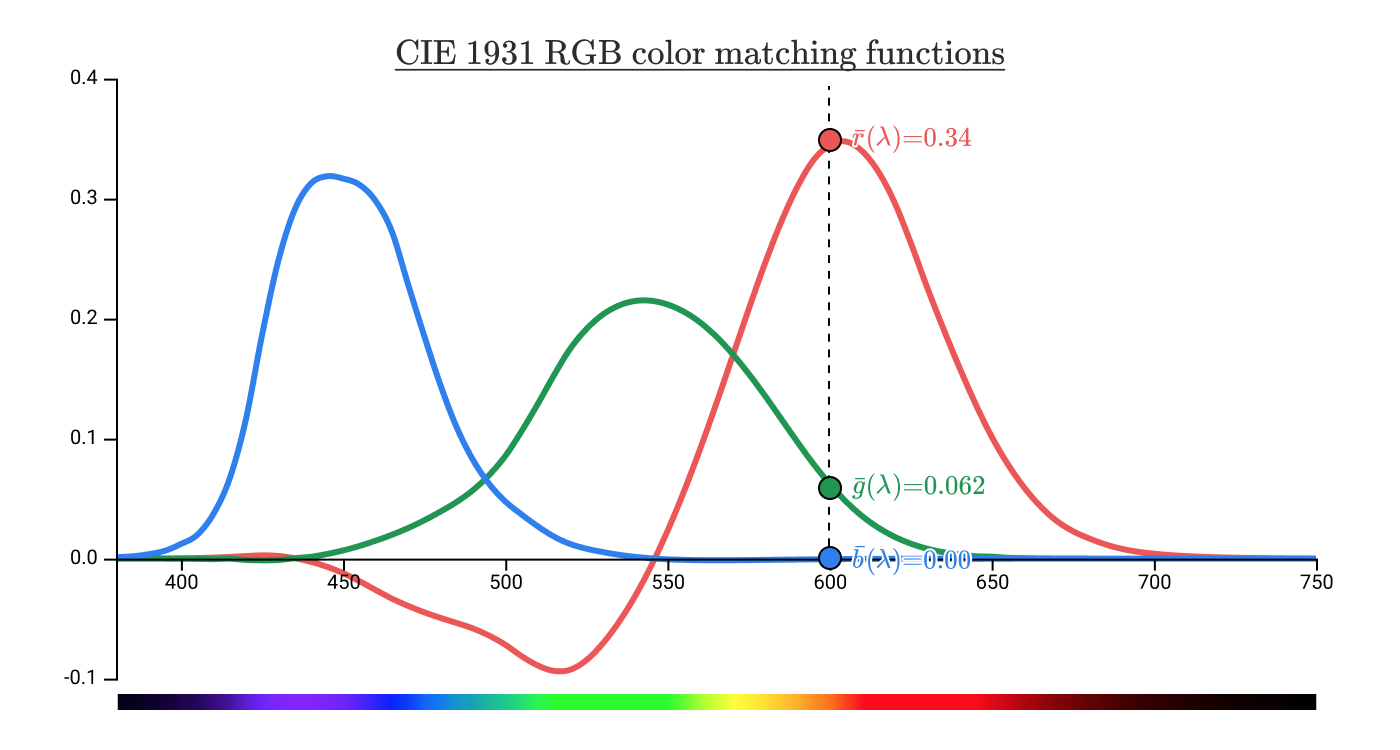
それらは、600 nmの波長に関連付けられている明確なスペクトル色を与えます。

（ R 、 G 、 B ）

$（R、G、B）$ 座標（0.34、0.062、0.00）。これは、 CIE 1931 RGB色空間の色の値です。

待って、関数の負の値はどういう意味ですか？

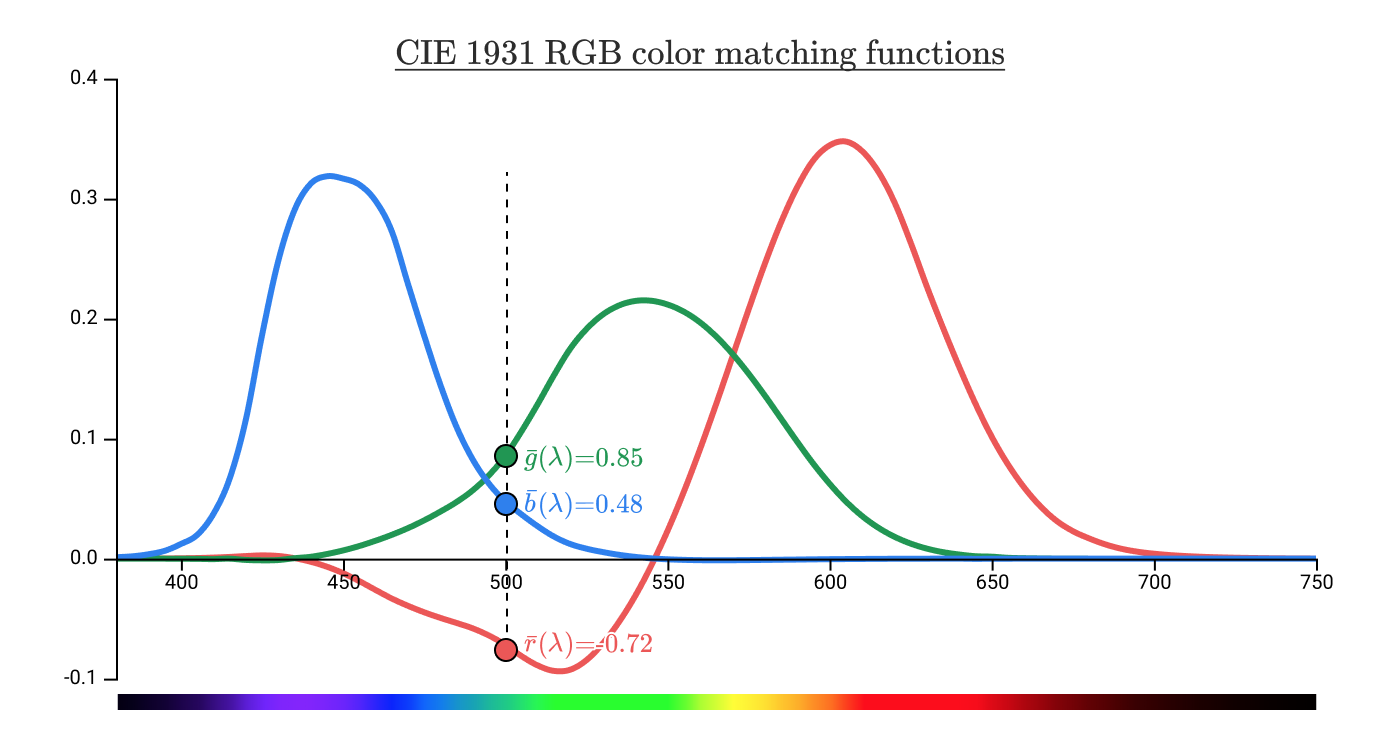
500 nmの波長の色に関連付けられている純粋なスペクトル色では、座標

（ R 、 G 、 B ）

$（R、G、B）$ 等しい（−0.72、0.85、0.48）。それでは–0.72とはどういう意味ですか？

上部の赤（700 nm）ランプのパラメーターでは、上部の青と緑のランプの出力に関係なく、下部の500 nmの色と一致させることはできません。しかし、赤いランプを下に動かすことで、両側で一致させることができます。

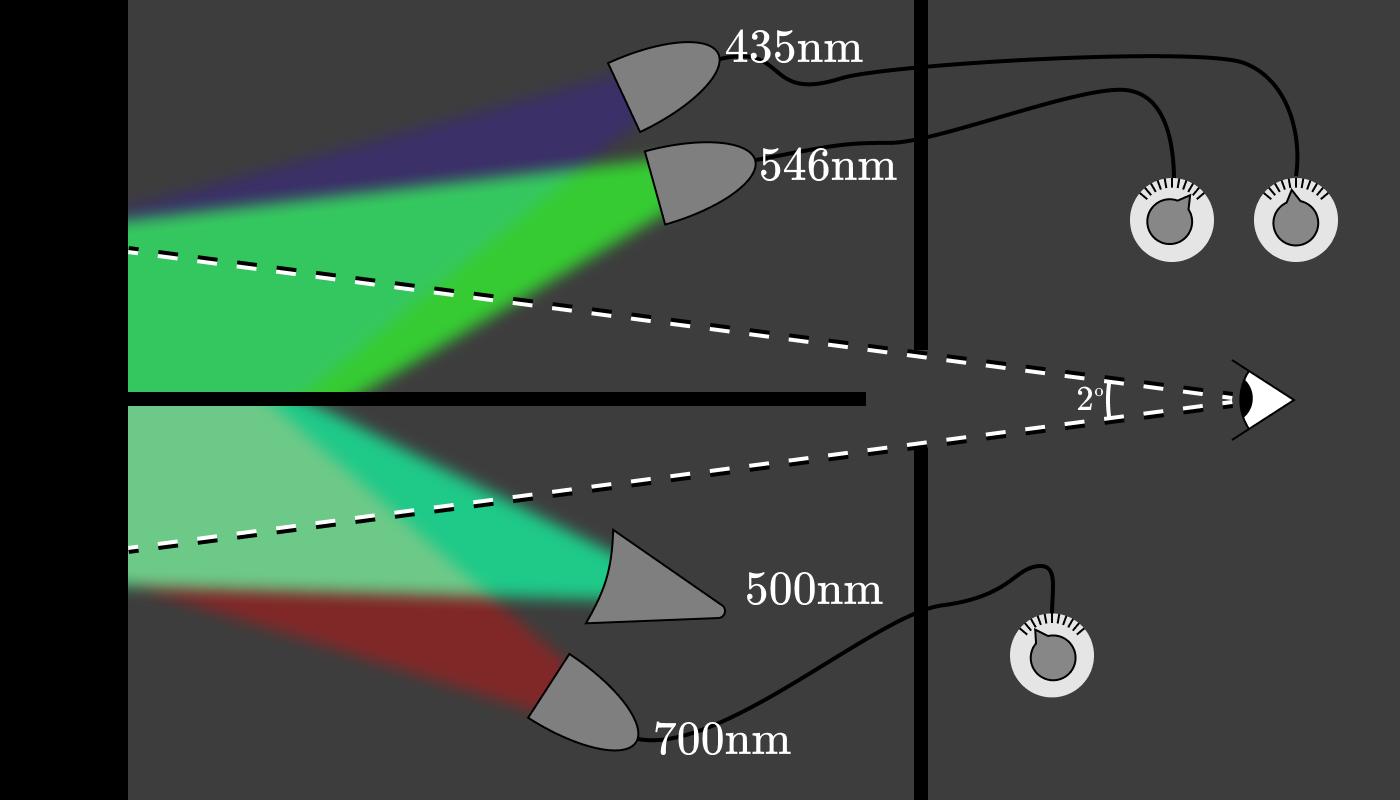
実際の実験セットアップでは、おそらく、固定波長の完全なランプセットが上下に設置されて、「ネガティブ」ゾーンで各ランプを調整しました。

色の組み合わせ機能を使用して、赤（700 nm）、緑（546 nm）、青（435 nm）の光の量を組み合わせて（負の場合もあります）単色光の一致を見つけることができます。

色を追加する機能は、コーンL、M、Sの感度を分析したのと同じ方法で分析できます。同じレモン色を使用します。

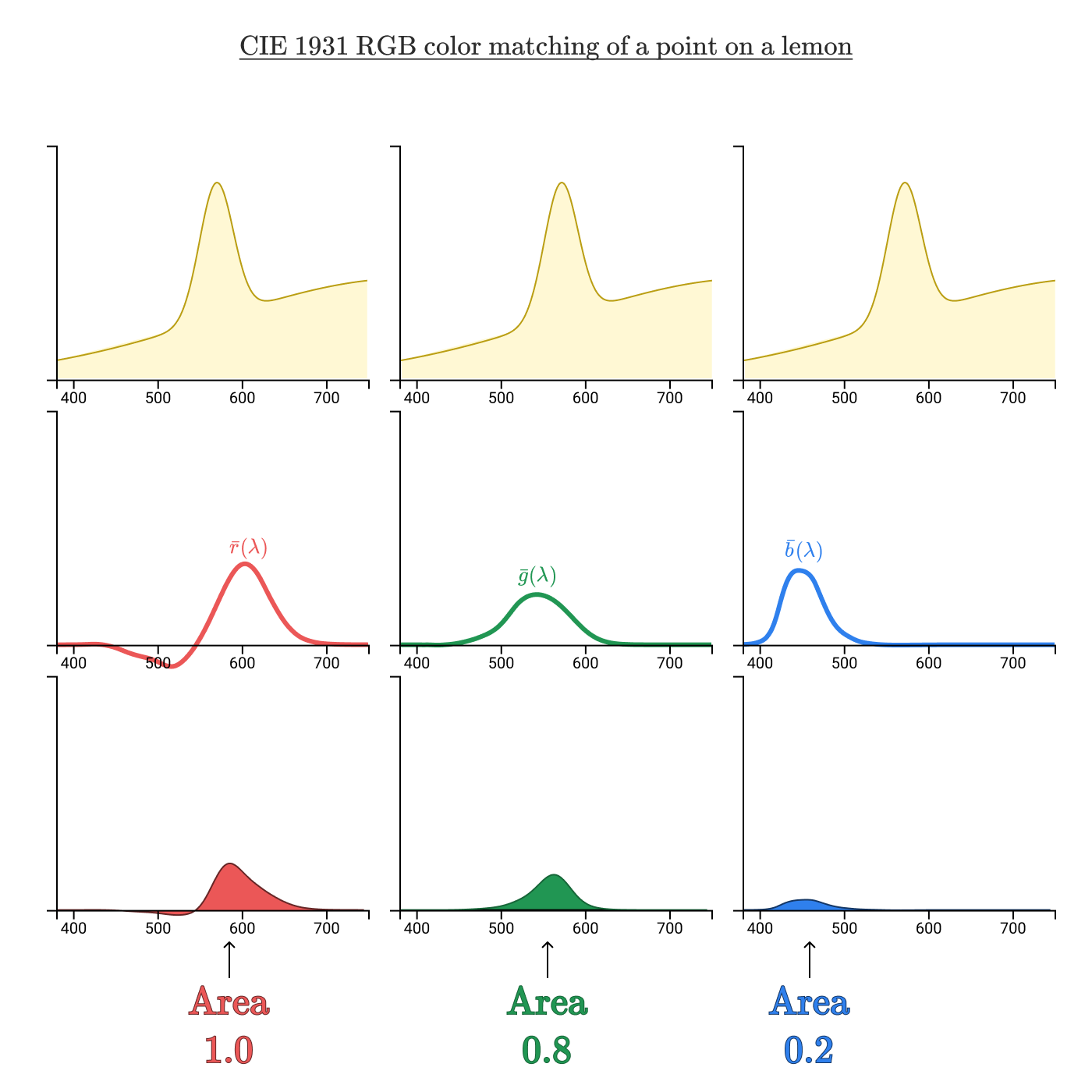
スペクトル曲線と色加算関数の積曲線で囲まれた領域を取得すると、この色を一意に識別するRGBトリプレット（1,0、0,8、0,2）が得られました。

色空間

（ L 、 M 、 S ）

$（L、M、S）$ 色、色空間を正確に決定できます

（ R 、 G 、 B ）

$（R、G、B）$ 負の座標を持つ色を除き、それを正確に再現する方法を提供します。

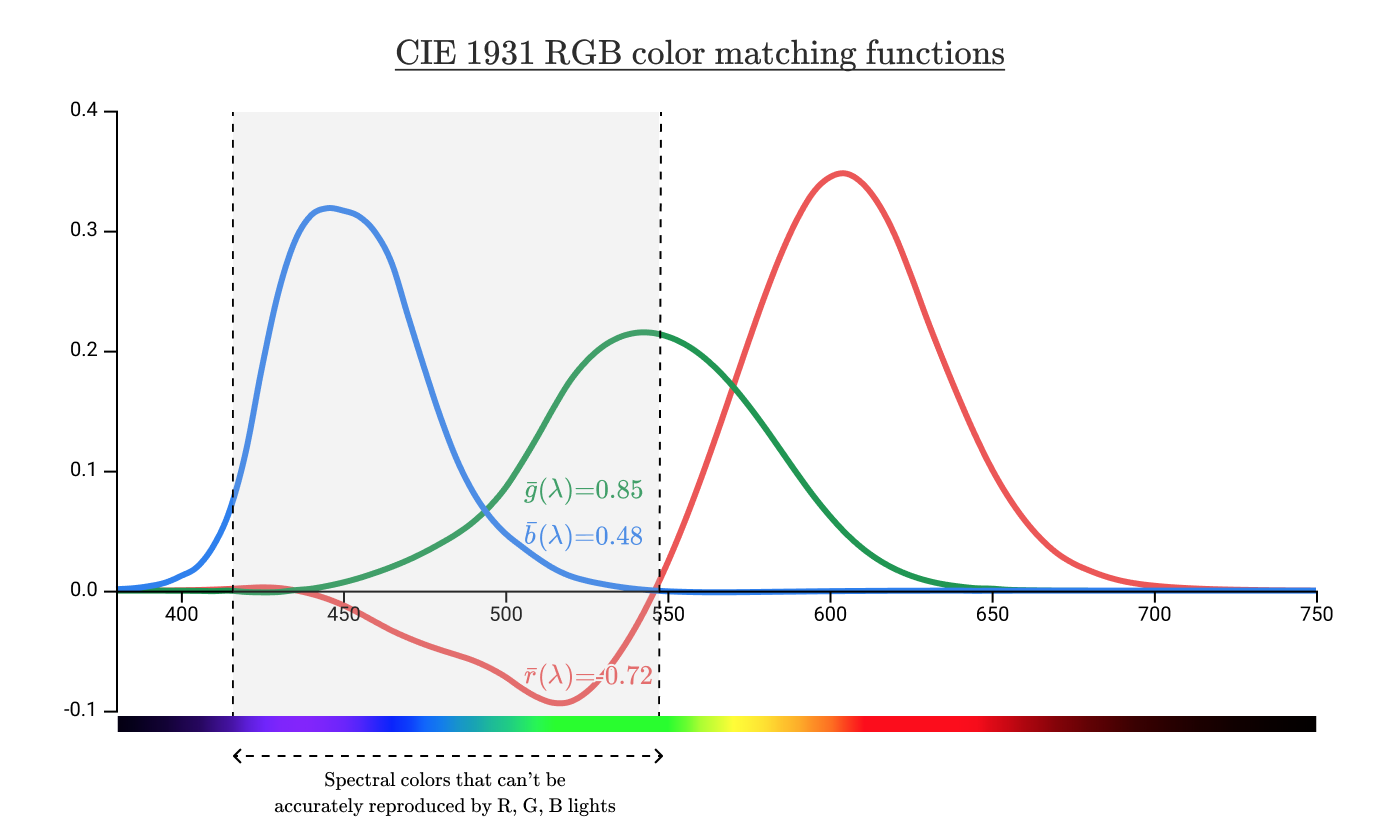
しかし、このグラフは、再現できないスペクトル色のみを示しています。非スペクトル色はどうですか？ R、G、Bの組み合わせでピンクを生成することは可能ですか？またはシアン（青緑色）？

これらの質問に答えるには、色空間を視覚化するより良い方法が必要です。

色空間と色度の可視化

これまで、ほとんどの図で、水平軸に沿って波長を配置し、いくつかのグラフを同じ平面に次々に配置してきました。

代わりに、関数として色を表すことができます

（ R 、 G 、 B ）

$（R、G、B）$ または

（ L 、 M 、 S ）

$（L、M、S）$ 。三次元空間で色がどのように見えるか見てみましょう

（ R 、 G 、 B ）

$（R、G、B）$ 。

いいね！虹のスペクトル色だけでなく、より広い範囲の色がここに表示されます。

2つの次元に縮小するには、値のペアごとに個別の図を作成するのが最も簡単です。次に例を示します。

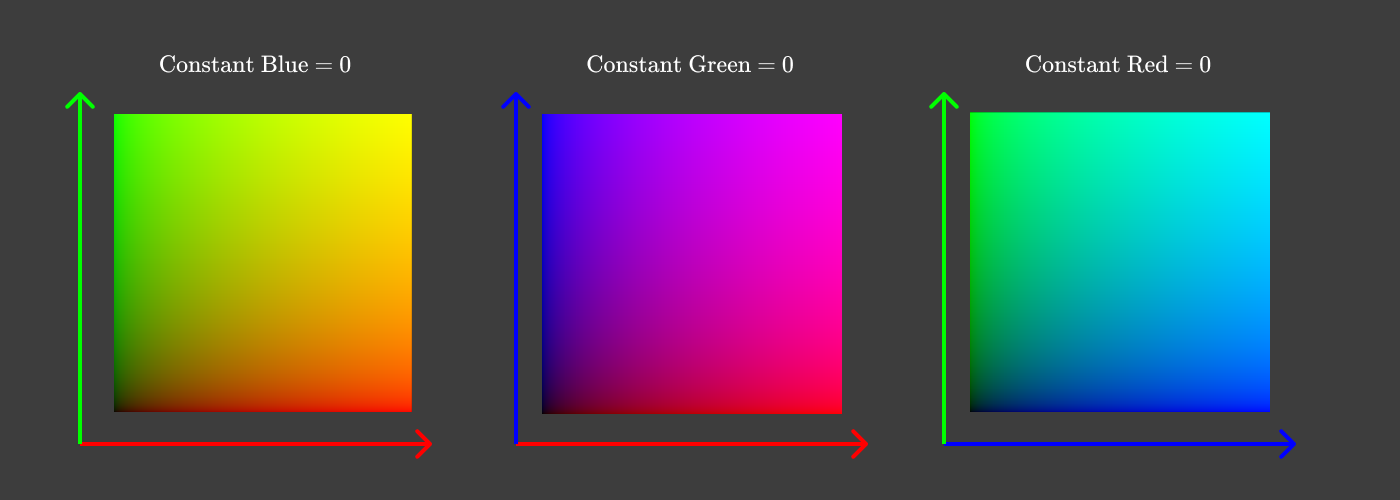
ゼロ3番目のコンポーネントを持つコンポーネントのペア

各図では、1つの次元を破棄し、3つの色成分の1つをゼロにしました。しかし、赤、緑、または青のコンポーネントを修正する代わりに、すべての色を見て、 明るさを修正する方が便利です。

キューブをもう一度見ると、（0、0、0）が黒に対応し、（1、1、1）が白に対応していることがわかります。

キューブを含む平面を斜めに切断するとどうなりますか

（ 1 、 0 、 0 ）

$（1、0、0）$ 、

（ 0 、 1 、 0 ）

$（0、1、0）$ そして

（ 0 、 0 、 1 ）

$（0、0、1）$ ？

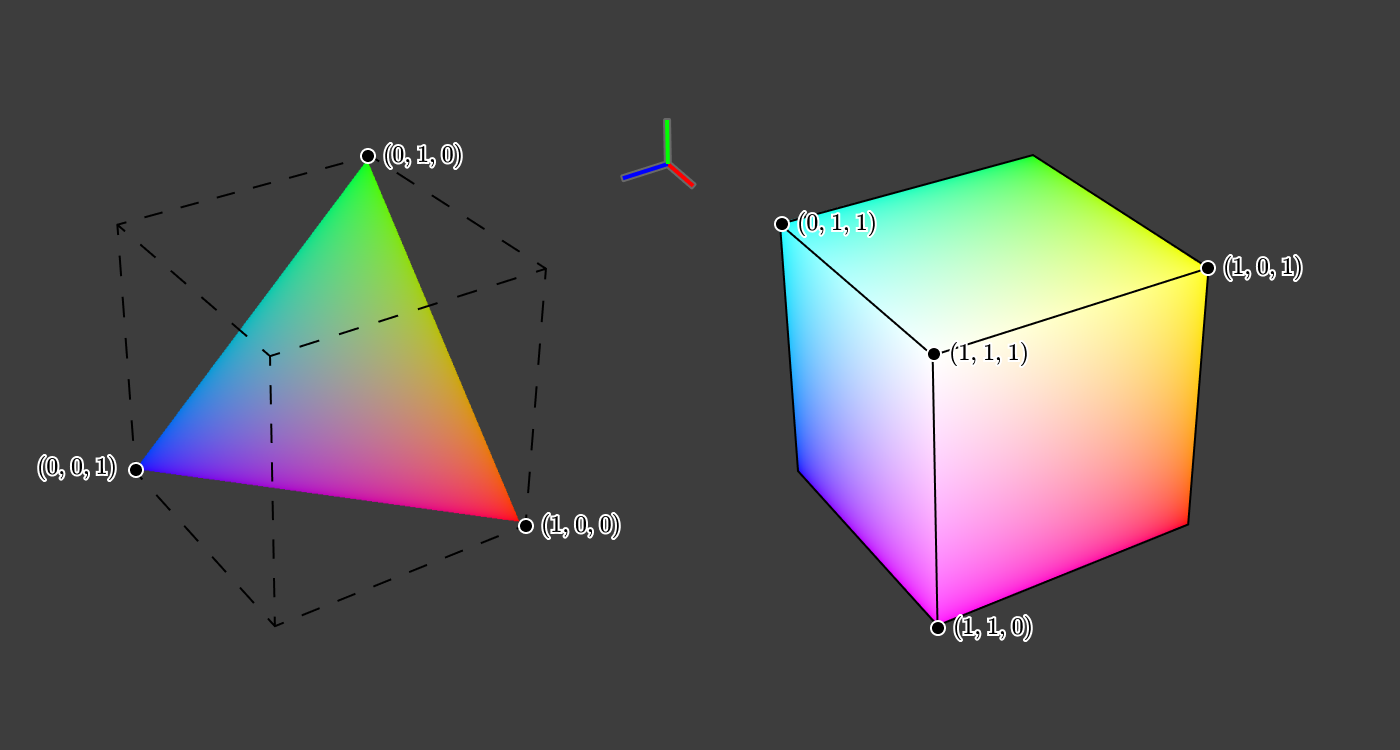
この立方体の三角形のスライスには、次のプロパティがあります。

R + G + B = 1

$R + G + B = 1$ そして私達は使用できます

R + G + B

$R + G + B$ 明度の大まかな近似のように。上から三角形のスライスを見ると、これが得られます：

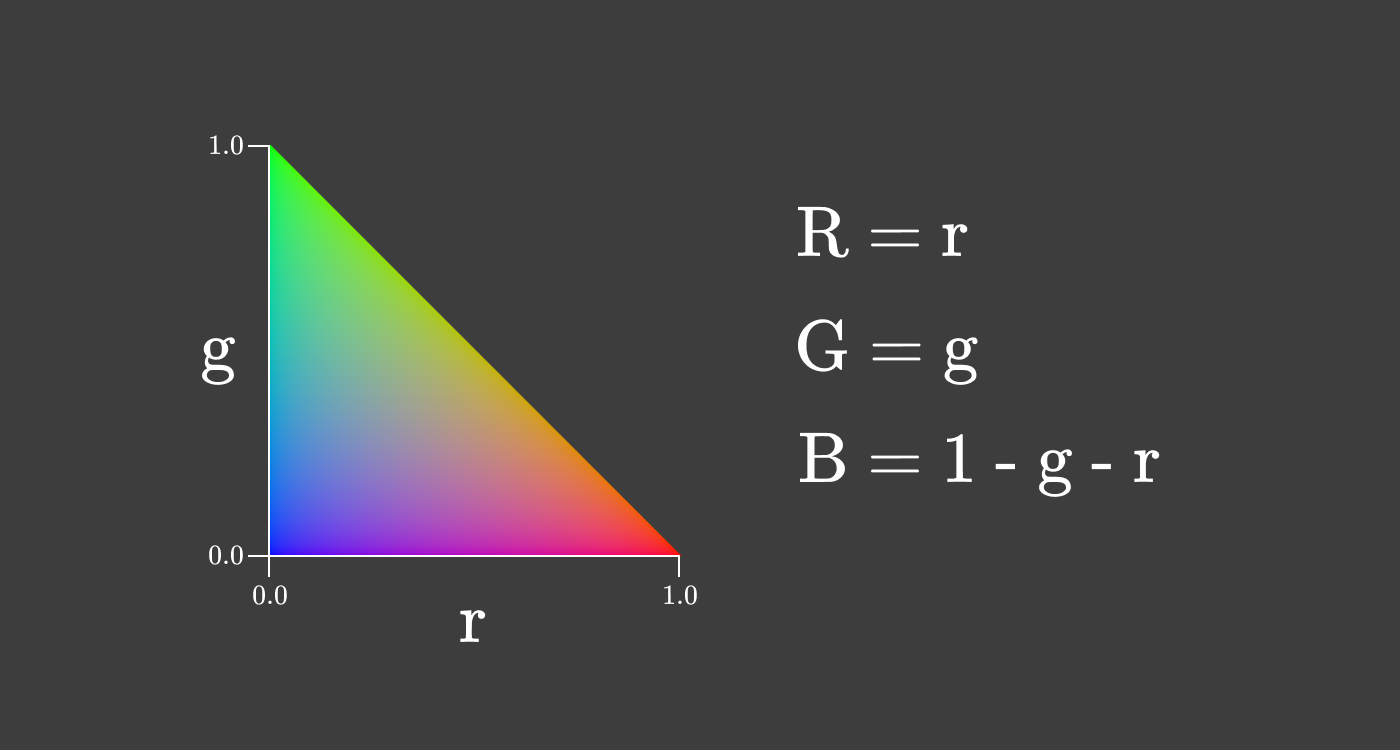
色のこの2次元表現は色度と呼ばれます。この特定の種はrg-chromaticityと呼ばれます。色度は、明度に関係なく、原色の比率に関する情報を提供します。

これは、異なる色度レベルで同じ色度を維持できることを意味します。

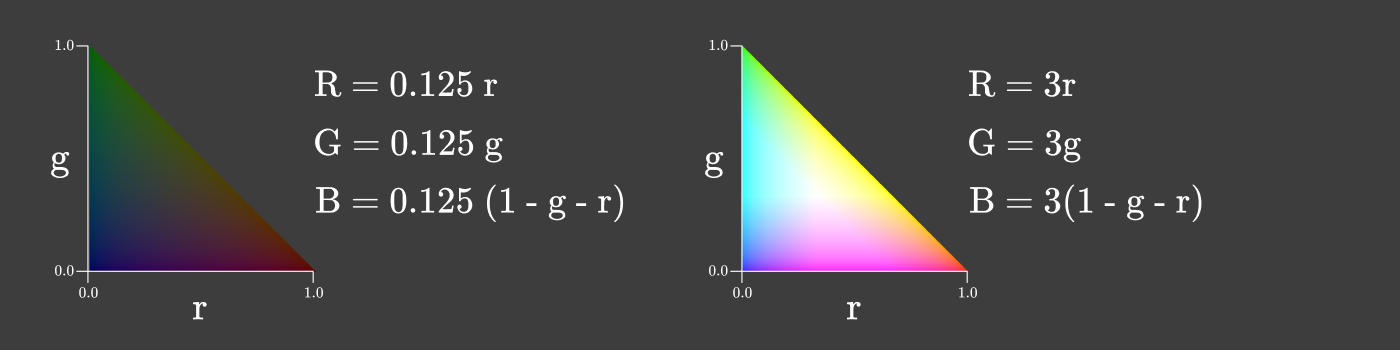
強度がrとgと共に変化する色度図を作成して、R、G、Bの関係を維持しながら強度を最大化することもできます。

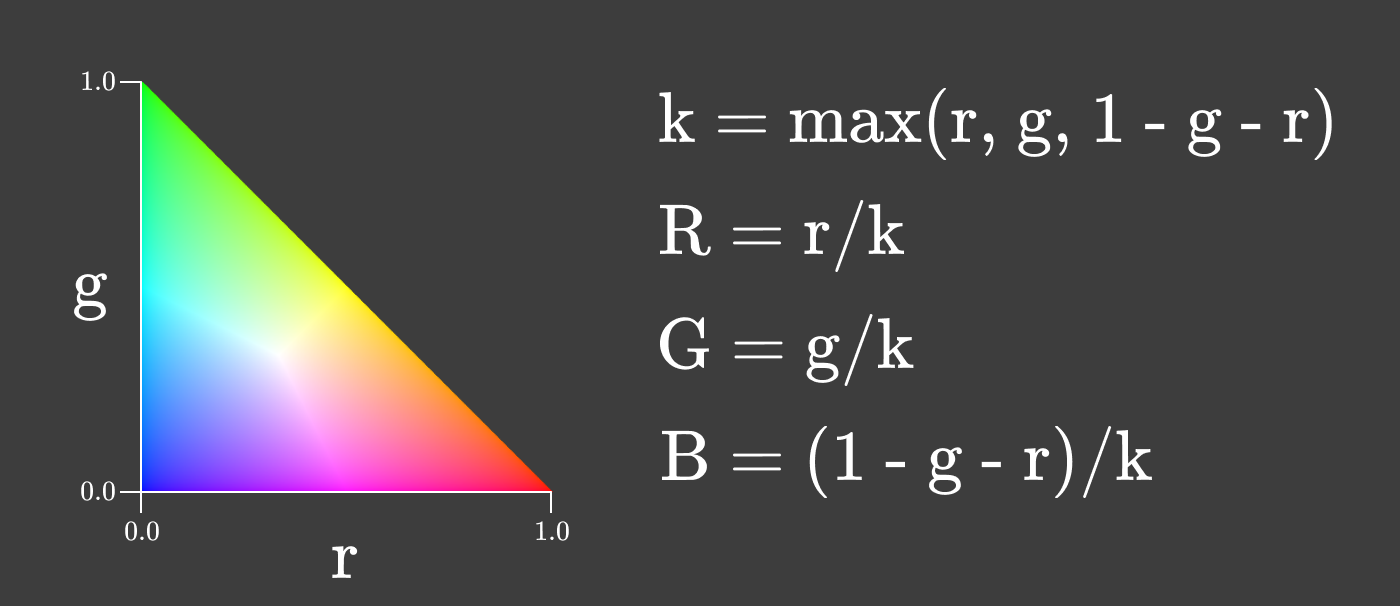
色度は色の有用な特性です。光源のスペクトル構成が同じであれば、光源の強度が変化しても色度は変化しないためです。画面の明るさが変化しても、色度は一定のままです！

色度を2つの次元に分割する方法は多数あります。一般的な方法の1つは、HSLおよびHSV色空間で使用されます。両方の色空間で、色度は「色相」と「彩度」に分けられます。

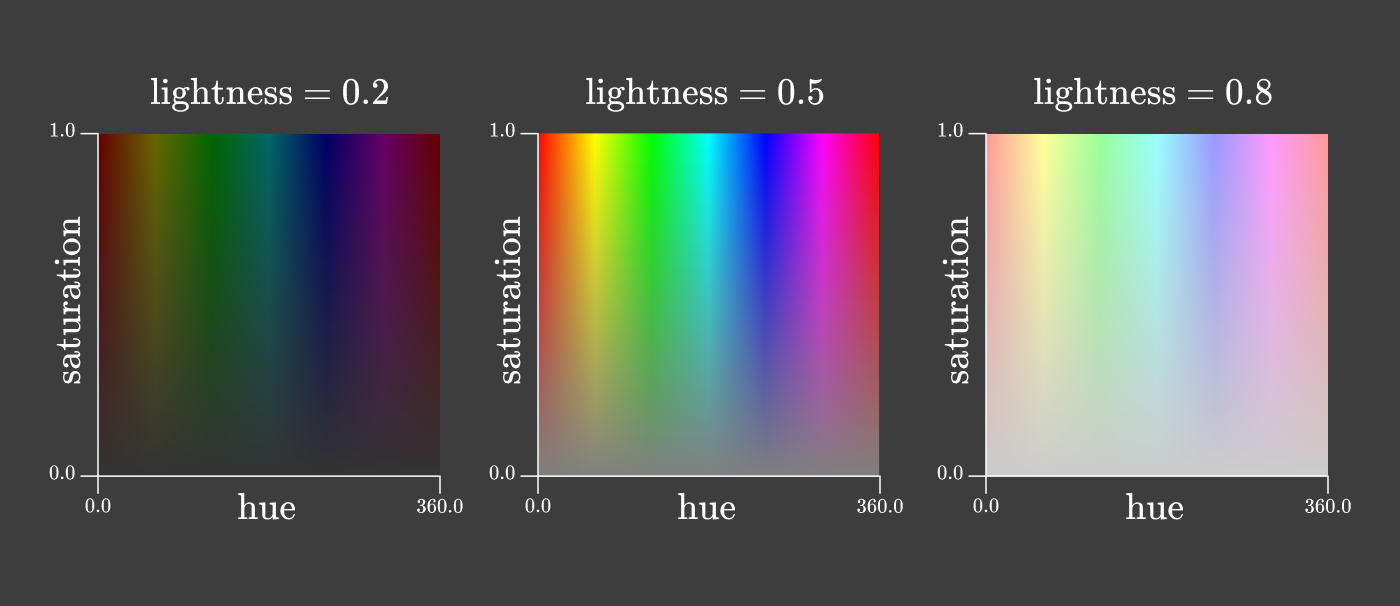
一見したところ、rg色度三角形とこれらの色相/彩度の正方形には虹のすべての色が含まれているように見えます。さて、色の追加機能でそれらの迷惑な負の値に戻る時間です。

ガンマおよびスペクトル軌跡

色追加機能を使用する場合

\bar{r} (λ)

$\bar r(\lambda)$ 、

\bar{g} (λ)

$\bar g(\lambda)$ そして

とビルドRG-色度スペクトル色は、あなたがおおよそのスケジュールを取得：黒の曲線を示し、純粋なスペクトル色の色のドットの色度。この曲線はスペクトル軌跡と呼ばれます。アスタリスクは、色追加実験で使用されたランプの波長に対応しています。この図に以前の色度の三角形を配置します。スペクトル軌跡内の領域には、人間に見えるすべての色が含まれています。市松模様の領域は、人が知覚する色を示していますが、不可能です。

\bar{b} (λ)

$\bar b(\lambda)$

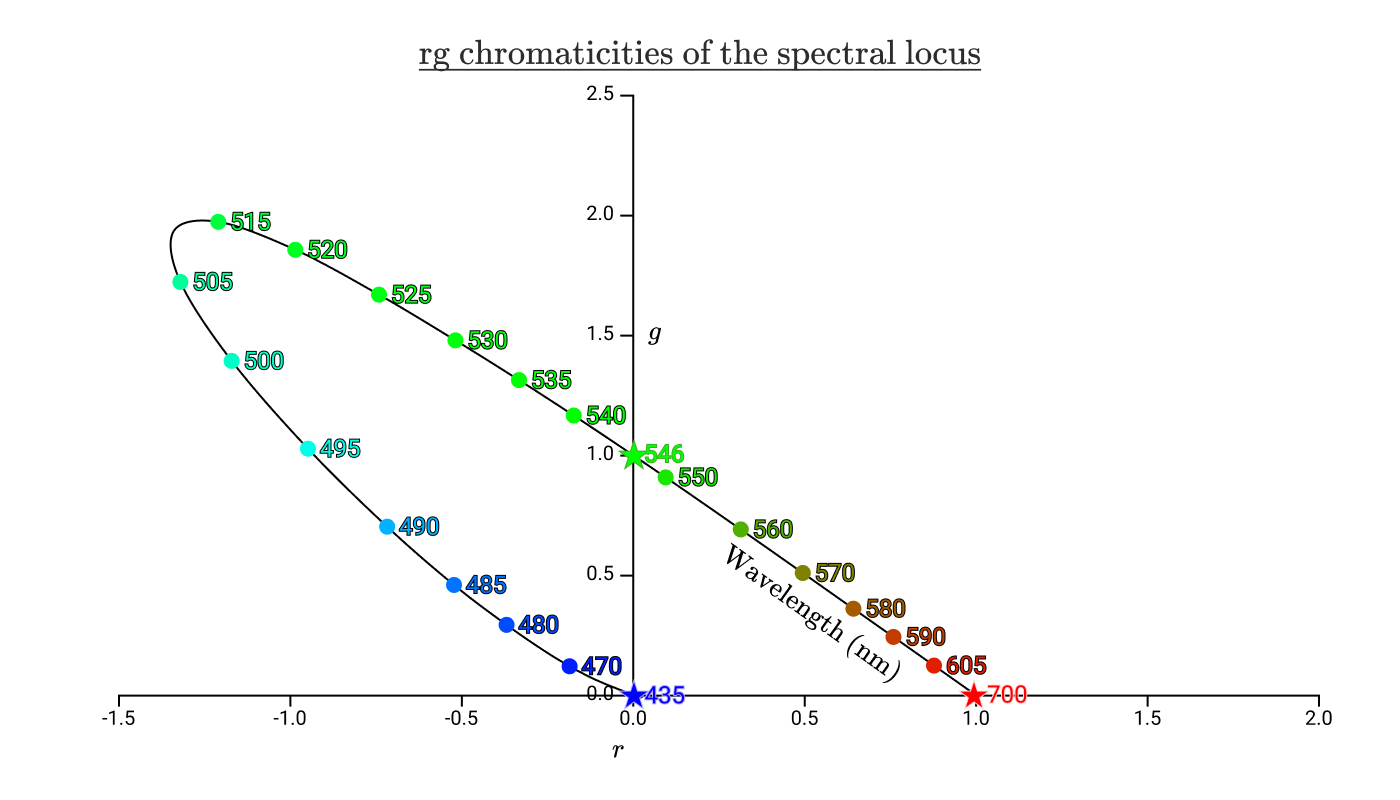
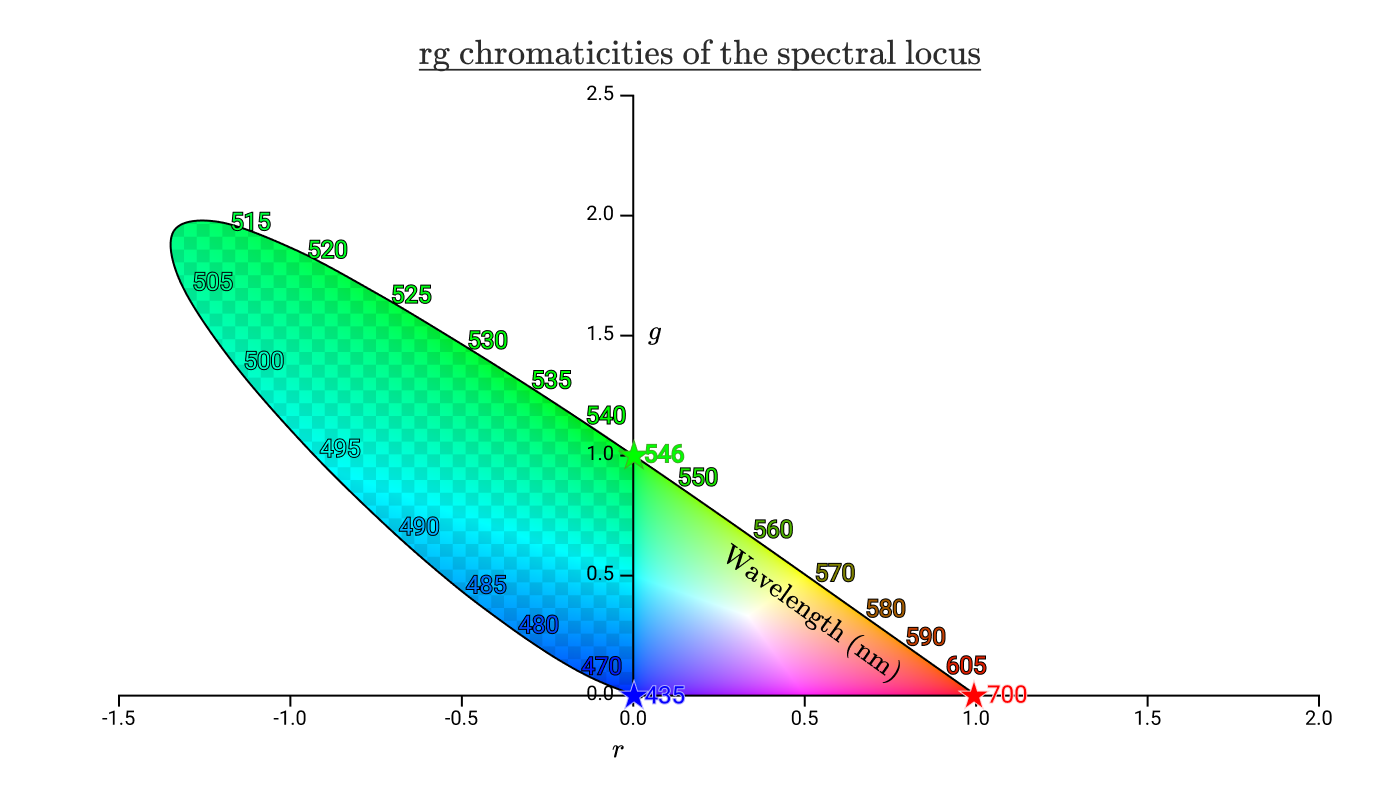
435 nm、546 nm、700 nmの波を追加して再現します。この図から、純粋なシアンを含む435 nm〜546 nmのスペクトル色を再現できないことがわかります。

チェッカーのない右側の三角形は、R、G、Bの正の値によって再現できるすべての色です。この領域を色空間の色域と呼びます。最終的に 16進コードに戻る

前に、別の色空間を考慮する必要があります。

CIE XYZ色空間

1931年、国際照明委員会が召集されました。彼女は2つの色空間を設定しました。1つ目は、ライトとギルドの色合成実験から作成された、すでに説明したRGB色空間です。2番目はXYZ色空間でした。

XYZ色空間のタスクの1つは、人間に見えるすべての色に対して正の値を取得し、すべての色度値が両方の軸で[0、1]の範囲になるようにすることです。これを行うために、RGBスペースの適切な線形変換を慎重に選択しました。

[\begin{matrix} X \\ Y \\ Z \end{matrix}] = \frac{1}{b_{21}} [\begin{matrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{matrix}] [\begin{matrix} R \\ G \\ B \end{matrix}] = \frac{1}{0.17697} [\begin{matrix} 0.49000 & 0.31000 & 0.20000 \\ 0.17697 & 0.81240 & 0.010630 \\ 0.0000 & 0.010000 & 0.99000 \end{matrix}] [\begin{matrix} R \\ G \\ B \end{matrix}]

$\begin{bmatrix} X \\ Y \\ Z \end{bmatrix} = \frac{1}{b_{21}} \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix} = \frac{1}{0.17697} \begin{bmatrix} 0.49000 & 0.31000 & 0.20000 \\ 0.17697 & 0.81240 & 0.010630 \\ 0.0000 & 0.010000 & 0.99000 \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix}$

XYZ空間におけるrg色度の類似物はxy色度であり、色度図はより標準的な座標系に配置されます。

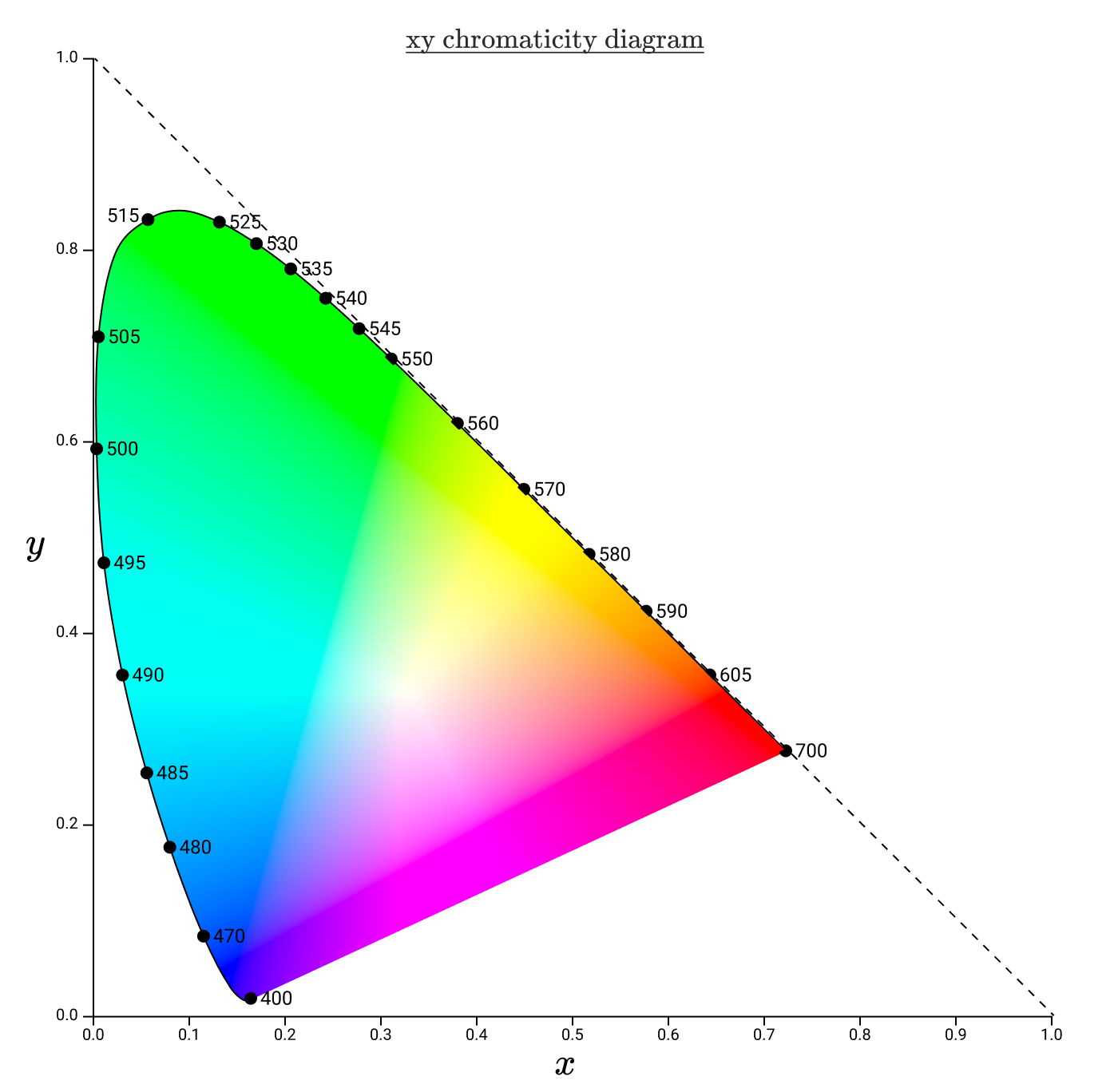
ガンマは通常、xy色度図の三角形で表されます。たとえば、今回は再びCIE RGB色域です。今回はxy空間です。

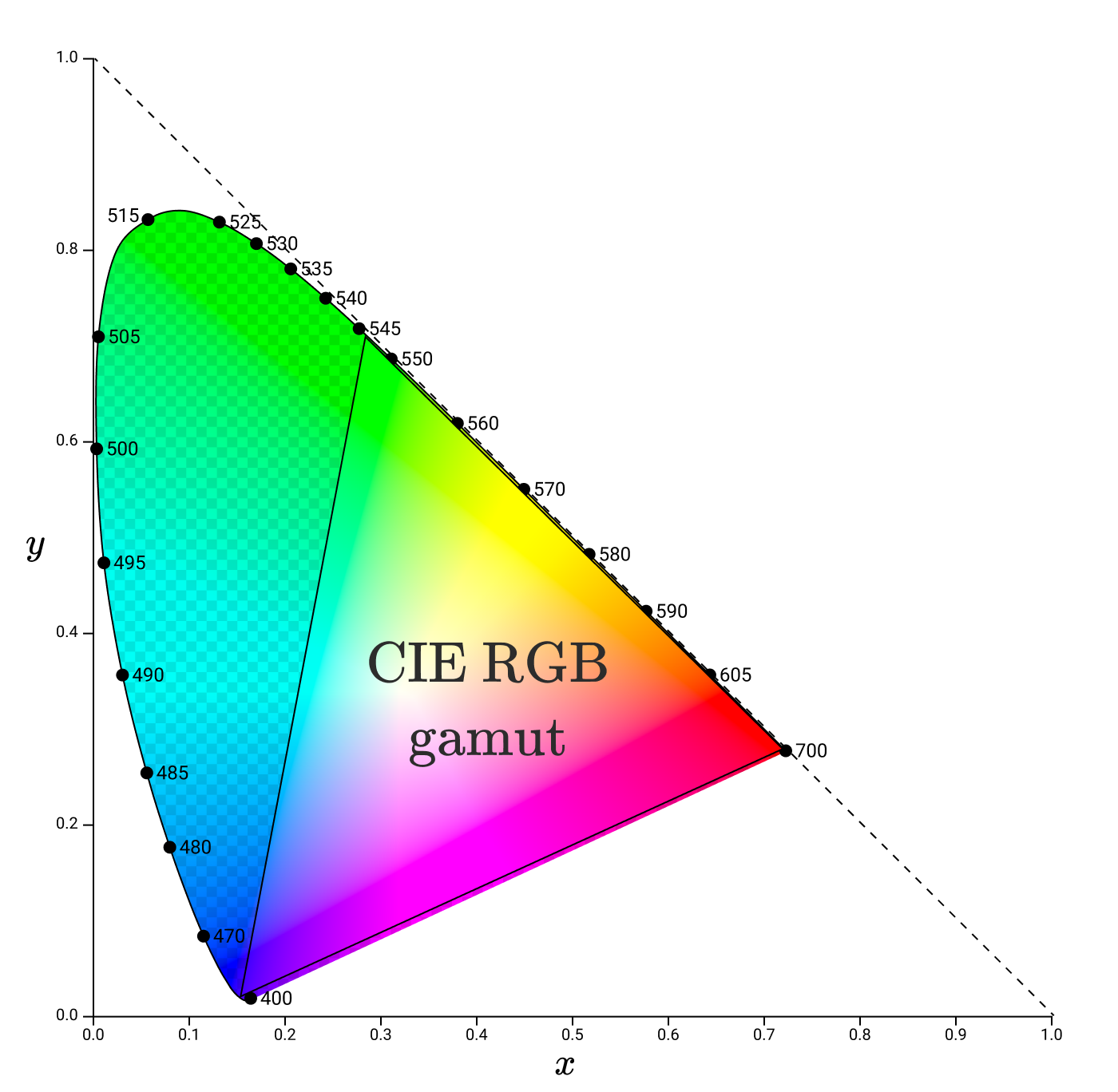
ガンマと色度を理解したので、デジタルディスプレイがどのように適切な色を表示できるかについて最終的に議論を始めることができます。

スクリーンのサブピクセル

ディスプレイのメーカーに関係なく、強い虫眼鏡の下にピクセルのグリッドが表示されます。各ピクセルは、赤、緑、青の3つのサブピクセルで構成されています。次のようになります。

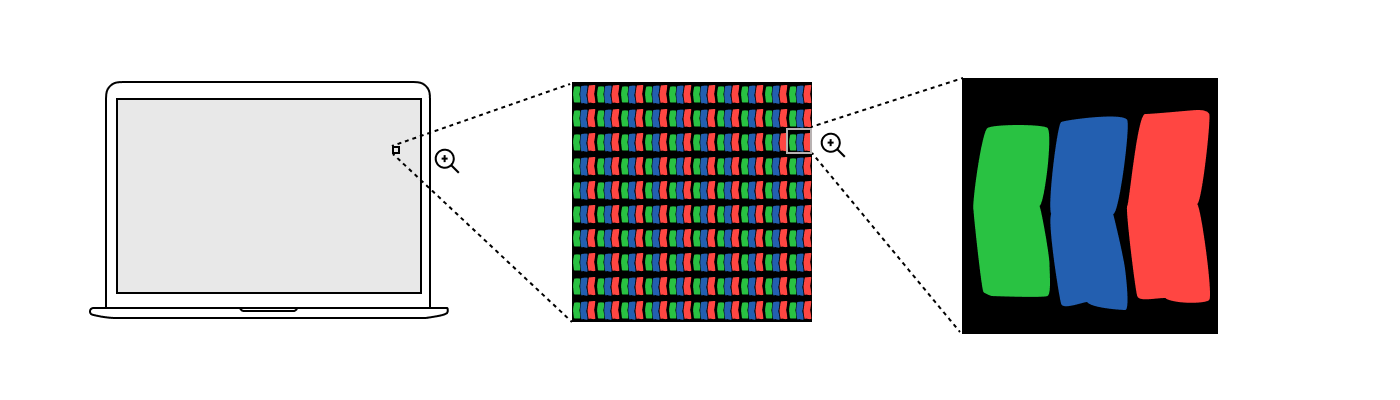
色追加実験のランプとは異なり、サブピクセルは単色の光を発しません。サブピクセルの各タイプには、モニターごとに異なる独自のスペクトル分布があります。f.luxometer

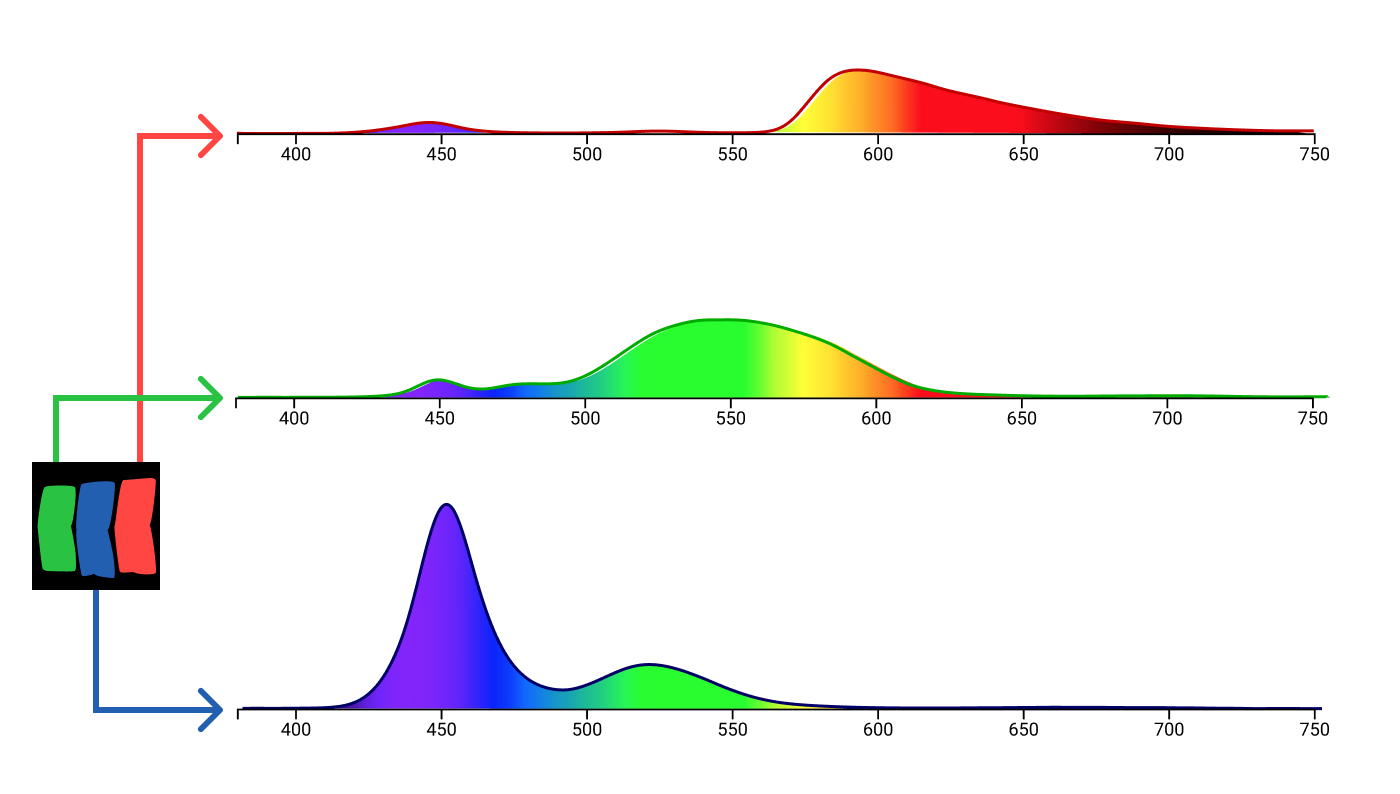
からのMacBook Airサブピクセルスペクトルデータ ColorSync

ユーティリティを使用して、Macbook Proのディスプレイのxy空間のガンマを決定しました。

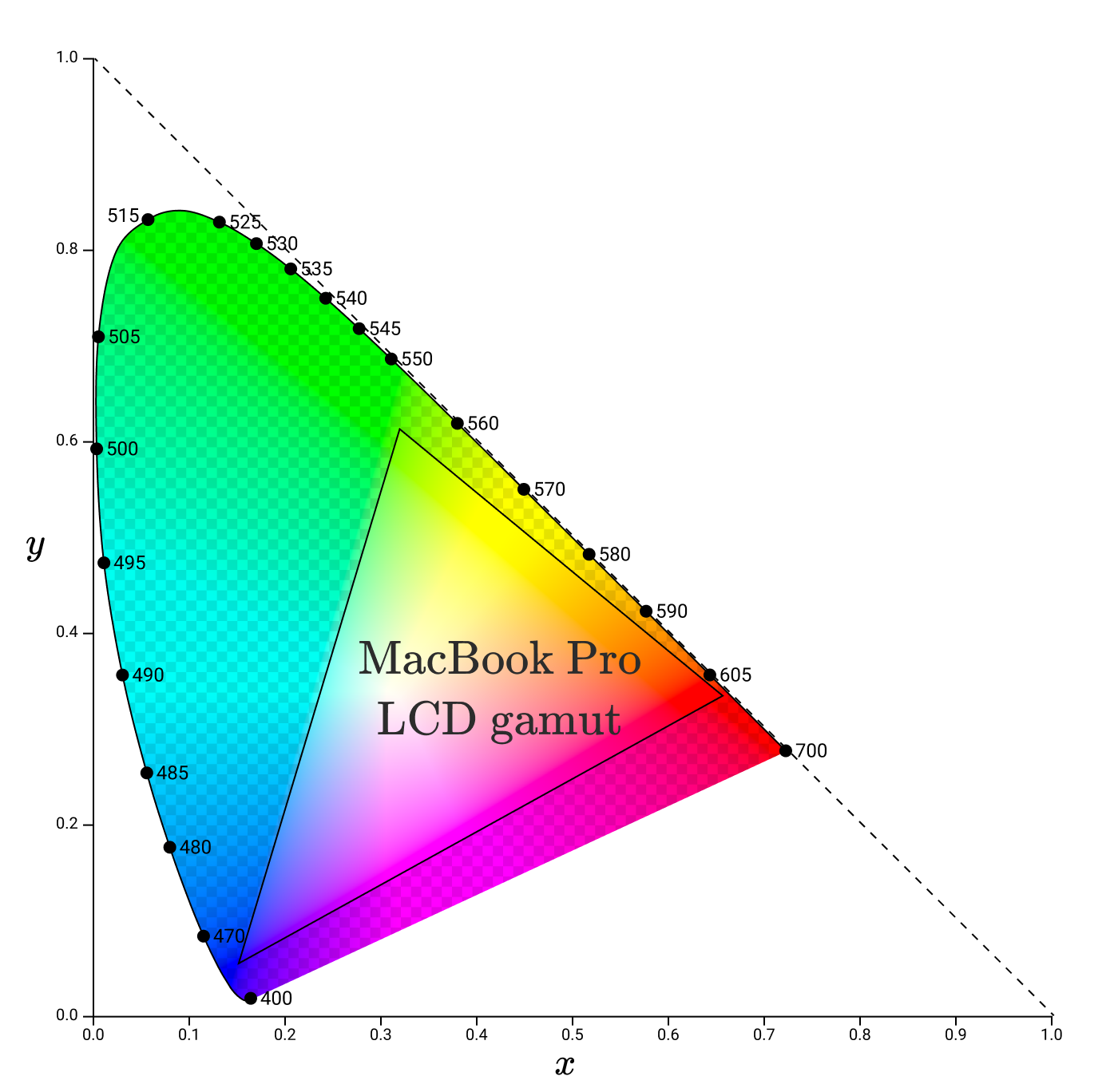
ガンマ角は、スペクトル軌跡に沿って存在しないことに注意してください。サブピクセルは純粋な単色光を放射しないため、理解できます。この色域は、このモニターが正確に再現できる原色のフルカラースペクトルを表します。

モニターの色域はさまざまですが、現代のモニターは特定の他の色域sRGBをカバーしようとする必要があります。

sRGB

sRGB（「標準の赤緑青」）は、異なるデバイス間で色情報を正確に送信するために1996年にHPとMicrosoftによって作成された色空間です。

この規格は、原色の色度を定義しています。

色度	赤	緑色	青
x	0.6400	0.3000	0.1500
y	0.3300	0.6000	0,0600
Y	0.2126	0.751	0,0722

それらを色空間に適用すると、MacBook LCDスクリーンの色域に似たガンマが得られますが、それより少し少なくなります。

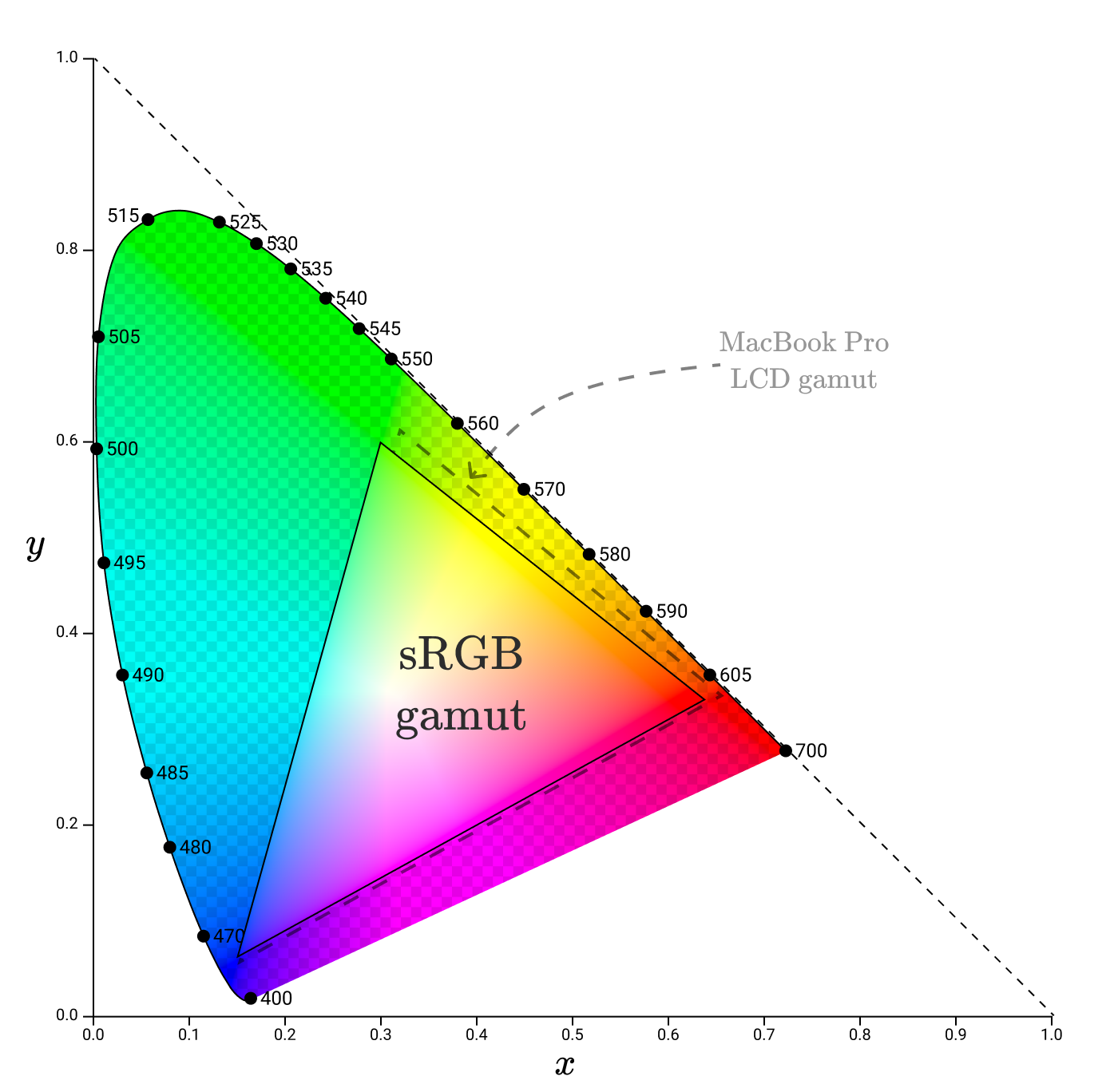
公式のsRGB色域の一部は、MacBook ProのLCD色域の一部ではないため、ディスプレイでは正確に再現できません。このため、MacBookは修正されたsRGB色域を使用しているようです。

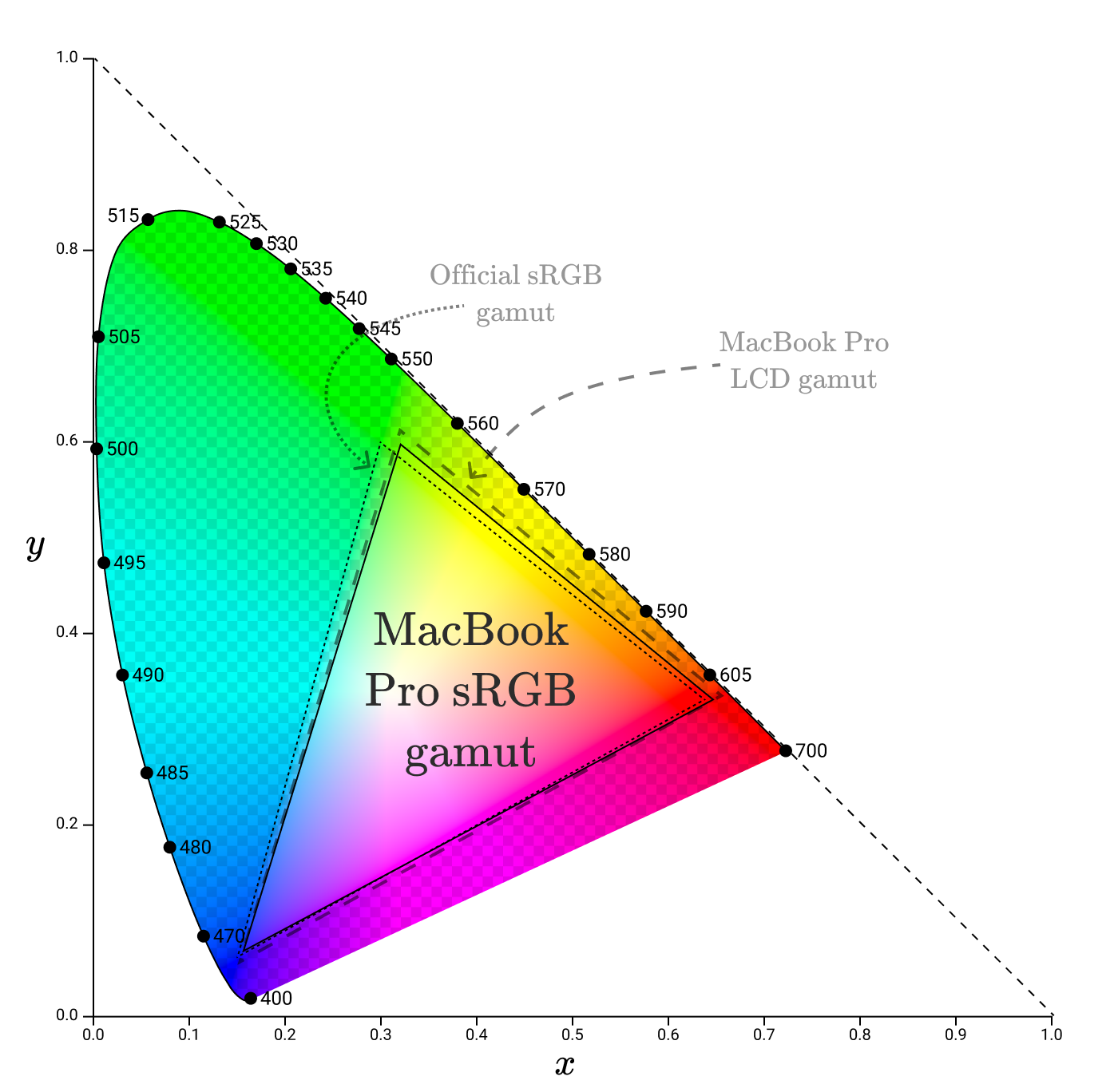
sRGBは、ほぼすべての場所で使用されるデフォルトの色空間です。これは、ブラウザの標準色空間です（CSS標準で指定されています）。この記事の図はすべてsRGB色空間にあります。これは、sRGB色域外のすべての色が図で正しく再現されないことを意味します！

これにより、最終的にインターネット上のカラーコードがわかります。

16進sRGBコード

#9B51E0

sRGB空間の色を設定します。これを対応する座標（R、G、B）に変換するには、3つのコンポーネントのそれぞれを0xFF

、つまり255で除算します。この場合：座標は色＃9BE1E0に対応します

0x9B / 0xFF = 0.61 
      

        
        
        
      

     0x51 / 0xFF = 0.32 
      

        
        
        
      

     0xE0 / 0xFF = 0.88

(0.61, 0.32, 0.88)

$(0.61, 0.32, 0.88)$ 。

これらの値をディスプレイに送信してサブピクセルの強度を設定する前に、もう1つのステップであるガンマ補正を実行する必要があります。

ガンマ補正

RGB空間の各座標に256個の可能な値がある場合、隣接する座標の各ペアが互いに可能な限り異なることを確認したいと思います。たとえば、その#030000

異なる#040000

方法#F40000

から#F50000

。

人間の視覚は、強い光よりも弱い光の小さな変化に敏感であるため、これらの256の値の多くを低光領域に配置することをお勧めします。

グレーの濃淡をエンコードしたいが、これには3ビットしかなく、8つの可能な値が得られると想像してください。

エネルギーの線形関数としてグレーの値を作成すると、次のようになります

。3ビット値と呼びましょう

Y

$Y$ 。すべての値が均等に分布している場合（

）、次の写真が表示されます：ご覧のように、知覚の違い

Y = \frac{⌊ 8 E ⌋}{8}

$Y = \frac{\left\lfloor8E\right\rfloor}{8}$

Y = 0

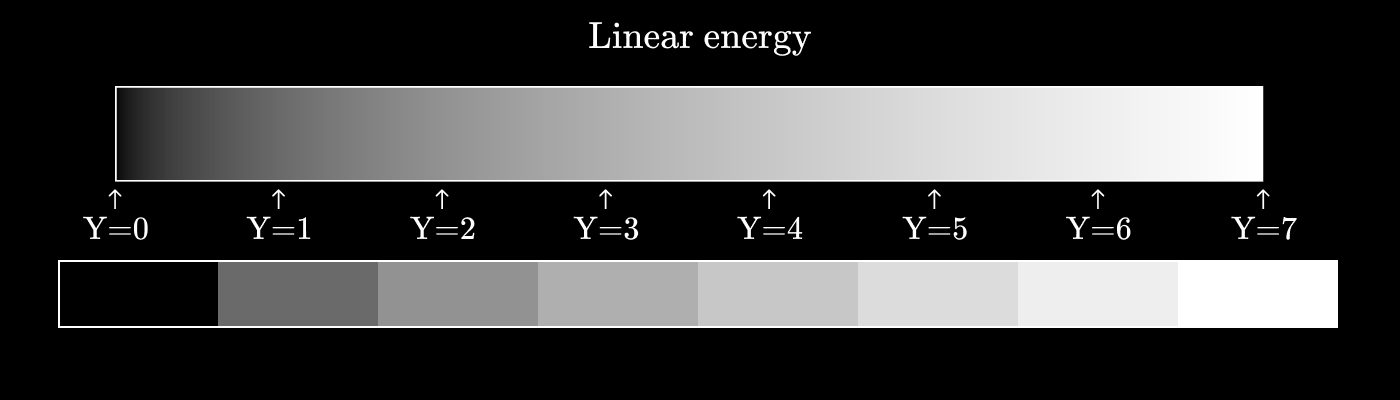
$Y=0$ そして

の間よりもはるかに大きいです

Y = 1

$Y=1$

Y = 6

$Y=6$ そして

Y = 7

$Y=7$ 。

次に、代わりにべき関数を使用した場合に何が起こるかを見てみましょう。やってみよう

知覚の均一性にはるかに近づいたため、値の各隣接ペアは、他の隣接ペアと同じ程度に異なります。このエネルギー値の離散値への変換は、ガンマコーディングと呼ばれます。逆の操作（離散値のエネルギーへの変換）はガンマデコードと呼ばれます。一般に、ガンマ補正は次の式に従って実行されます

Y = {(\frac{⌊ 8 E ⌋}{8})}^{2}

$Y = \left(\frac{\left\lfloor8E\right\rfloor}{8}\right)^2$

V_{o u t} = A V_{i n}^{γ}

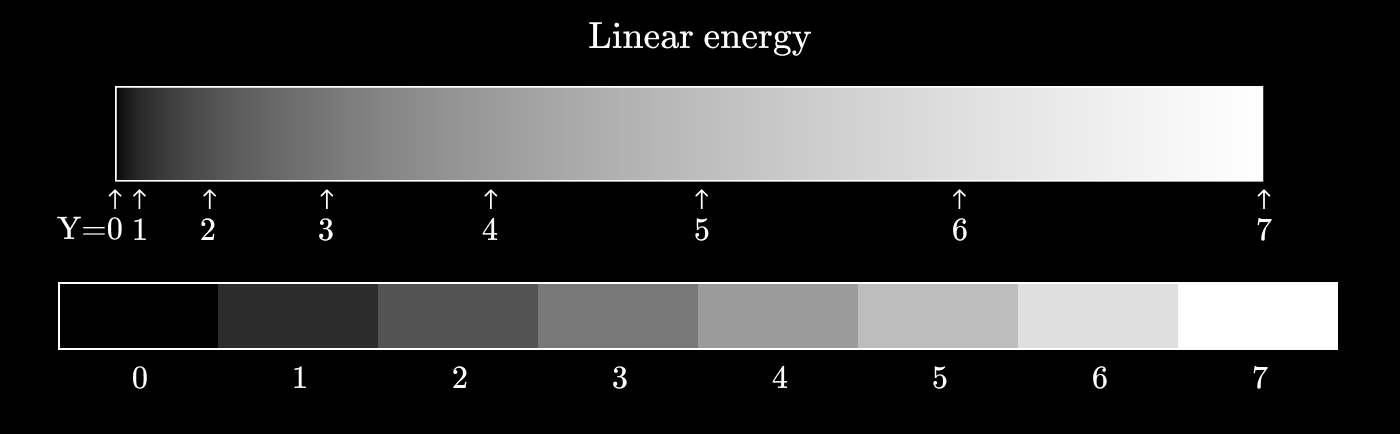
$V_{out} = A V_{in}^\gamma$ 。出展者は、ギリシャ語の文字「ガンマ」、したがって名前で示されます。

sRGBのコーディングとデコードのルールは同様の考えに基づいていますが、式はもう少し複雑です。

C_{l i n e a r} = {\begin{cases} \frac{C_{s R G B}}{12.92}, & C_{s R G B} \leq 0.04045 \\ {(\frac{C_{s R G B} + 0.055}{1.055})}^{2.4}, & C_{s R G B} > 0.04045 \end{cases}

$C_\mathrm{linear}= \begin{cases}\frac{C_\mathrm{sRGB}}{12.92}, & C_\mathrm{sRGB}\le0.04045\\ \left(\frac{C_\mathrm{sRGB}+0.055}{1.055}\right)^{2.4}, & C_\mathrm{sRGB}>0.04045 \end{cases}$

線形値に関してsRGB値を構築すると、次のグラフが得られます。

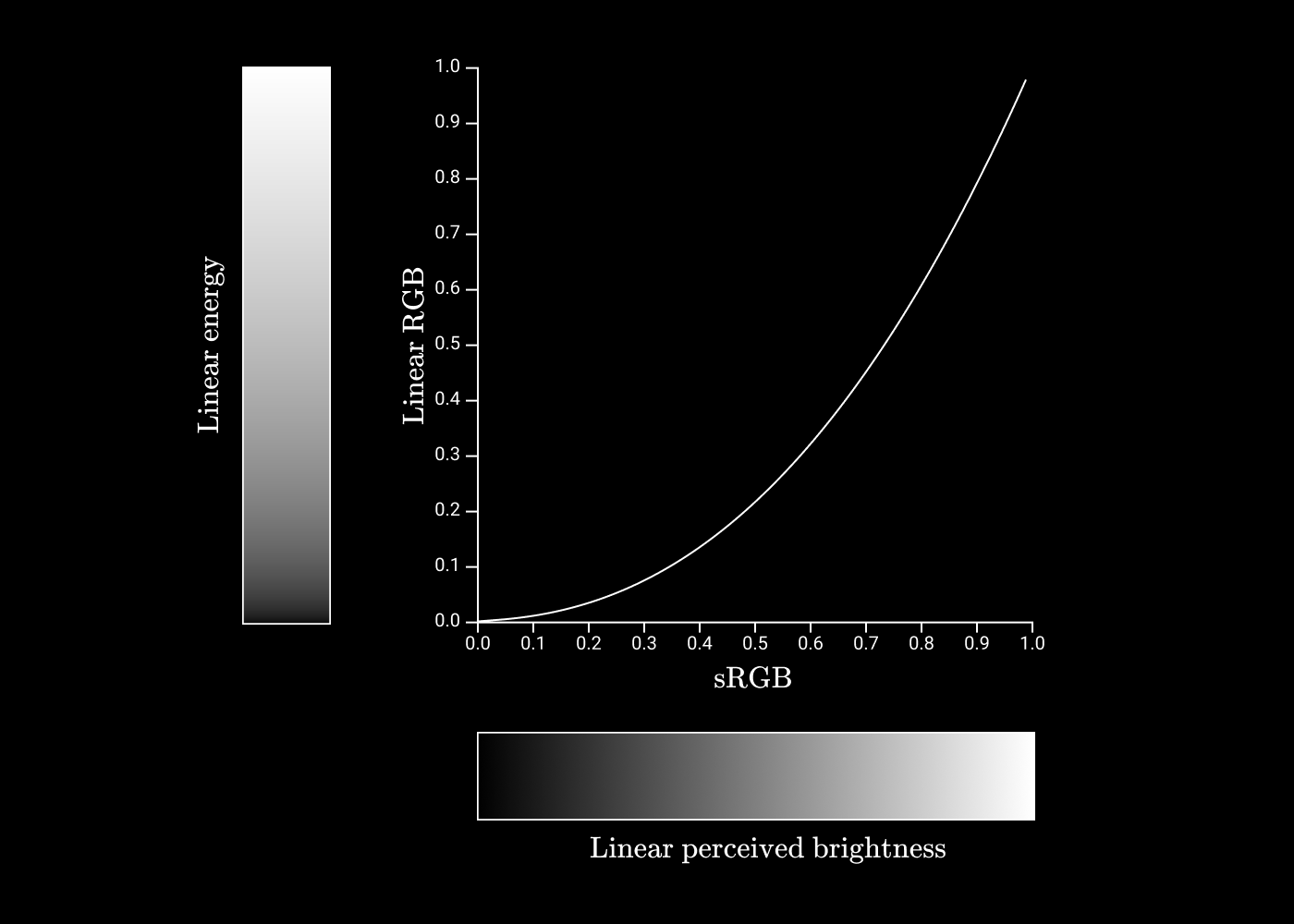
いいね！これは、16進コードから目の知覚に移行する方法を理解する最後のパズルです。ステップバイステップのガイドを作成します。

16進コードから目まで

まず、#9B51E0

コンポーネントR、G、Bに分割し、これらのコンポーネントを範囲内で正規化します

[0, 1]

$[0, 1]$ 。

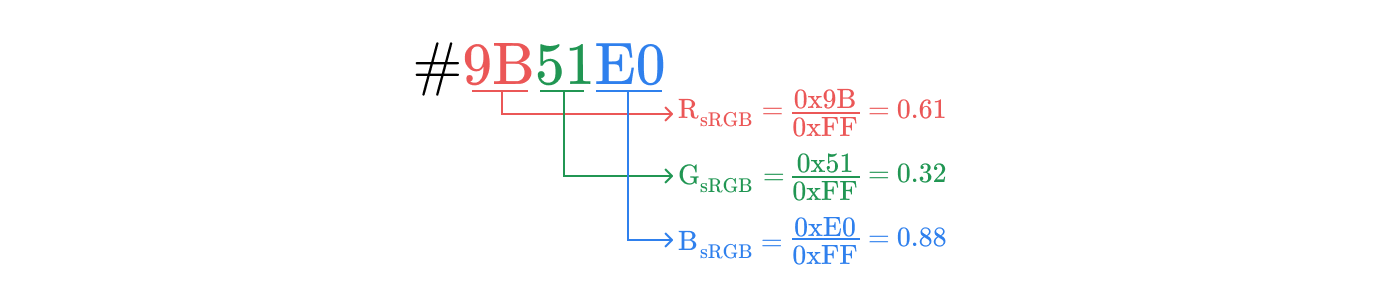
それは私たちに座標を与えます

sRGB空間です。次に、sRGBコンポーネントを取得し、線形値に変換します。それは私たちに座標を与えます

(0.61, 0.32, 0.88)

$(0.61, 0.32, 0.88)$

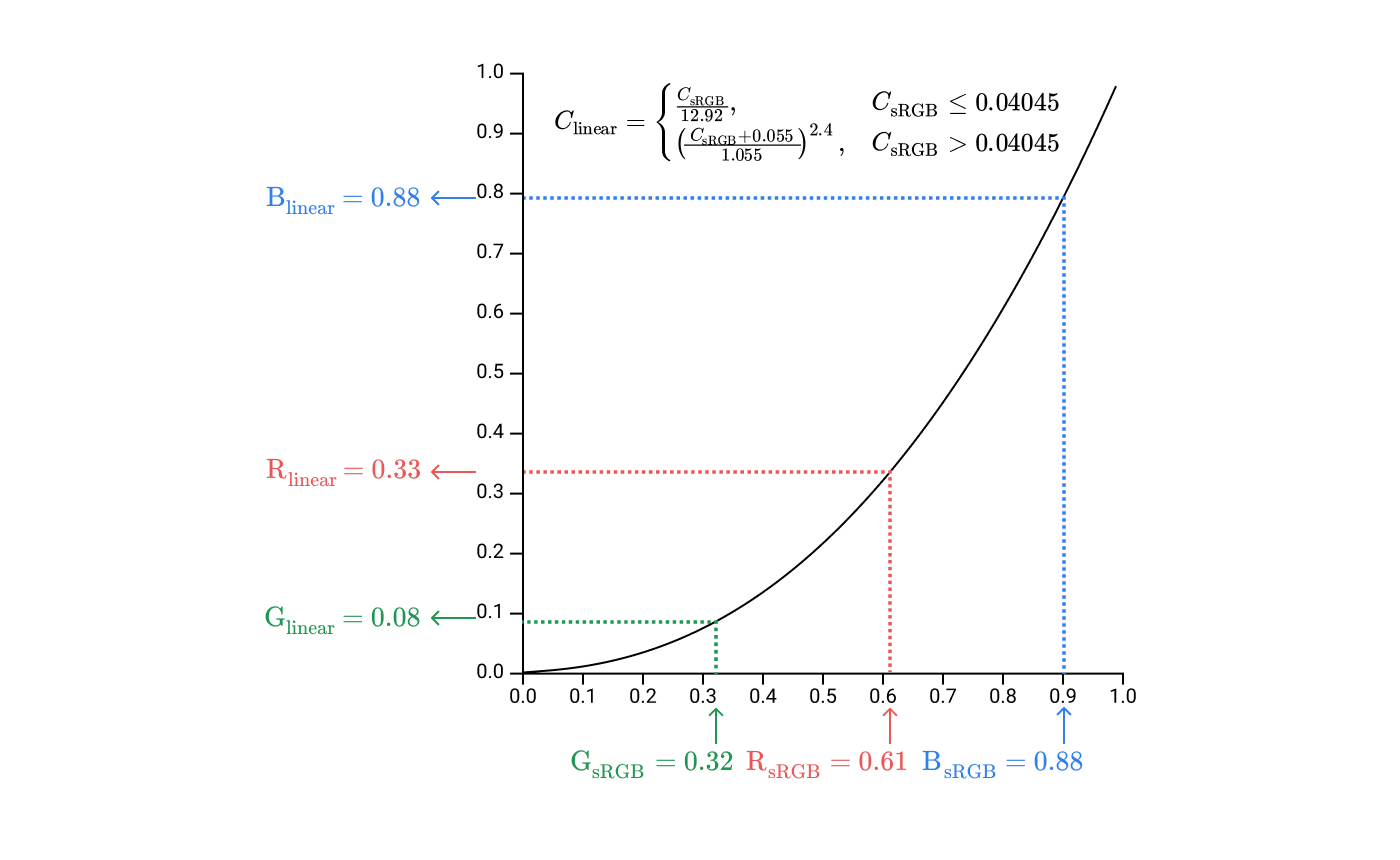
線形RGB空間です。これらの値は、画面上のサブピクセルの明るさを設定するために使用されます。サブピクセルのスペクトル分布は、ピクセル全体の1つのスペクトル分布に結合されます。ピクセルからの電磁放射は角膜を通過して網膜に到達し、3種類の錐体を刺激します。すべてのステージを組み合わせて、記事の最初から画像を取得します！

(0.33, 0.08, 0.10)

$(0.33, 0.08, 0.10)$

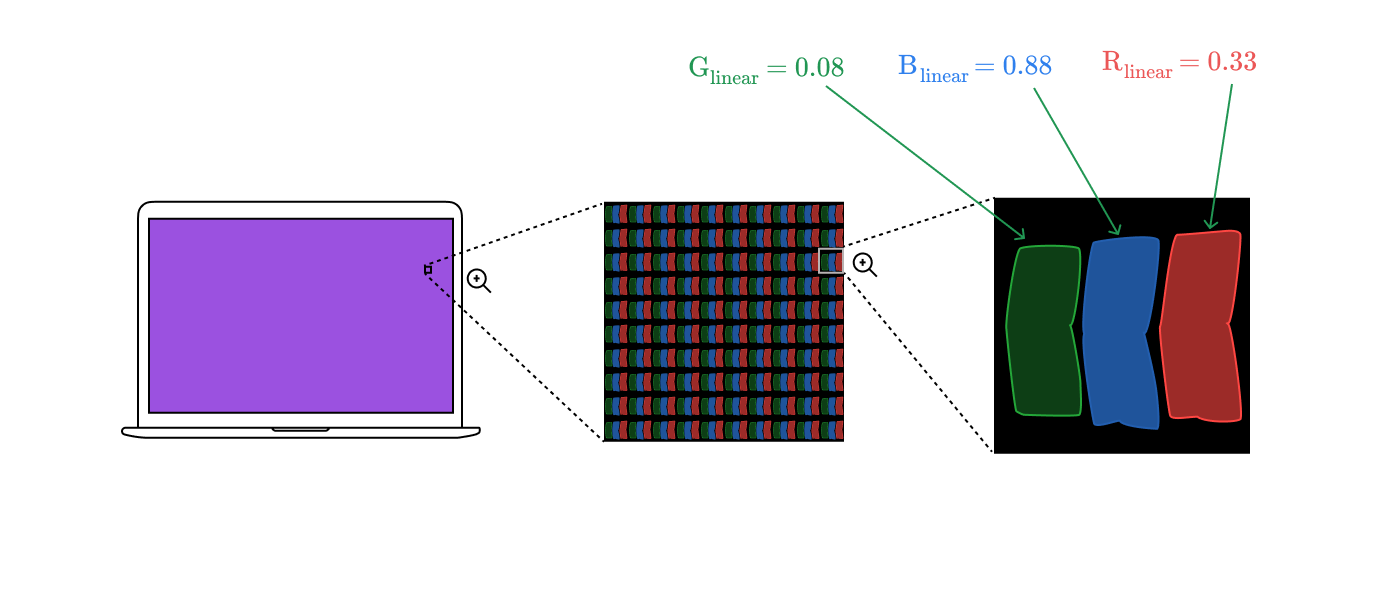
明るさの調整に関する簡単なメモ

sRGB値は、画面のサブピクセルの輝度に変換される前に、デバイスの輝度設定に従って減衰されます。したがって、0xff0000

輝度設定が50％の0x7F0000

画面の色は、輝度が100％の同じ画面の色に対応する場合があります。

完璧な画面で、黒いピクセル

にかかわらず、輝度設定のいずれか発光しません。ただし、ほとんどの携帯電話とラップトップはLCDパネルを使用しており、各サブピクセルは白色光に作用するフィルターです。次のビデオでは、LCDの仕組みが詳しく説明されています。

(0, 0, 0)

$(0, 0, 0)$

フィルターは不完全であるため、明るさが増すと、バックライトがフィルターから漏れると黒いピクセルが発光します。OLED画面（iPhone XやPixel 2の場合）では、バックライトが適用されないため、画面の明るさに関係なく一定の黒が表示されます。

逃したもの

この記事では、色のレンダリングと視覚の多くの側面を特に省略しました。たとえば、彼らは反対の色の理論や色の恒常性の効果で脳の錐体からの情報を処理することについて話しませんでした。加法混合と減法混色については話しませんでした。彼らは色覚異常（色覚異常）について話しませんでした。光束、光の強度、明るさ、照明、光放射の違いについては話しませんでした。ICCデバイスのカラープロファイルと、f.luxなどの色知覚プログラムで何をしているのかについては話しませんでした。

とにかく記事が長すぎることが判明したので、私は括弧から外しました。私の友人が言ったように、人生の多くのものが見た目よりも複雑であることを理解していても、色はあなたが予想したよりもさらに複雑になります。

参照資料

この記事を書いているとき、私は単に文献を読むのに異常に長い時間を費やしました。なぜなら、私はトピックの最も完全な開示に必要なますます新しい情報を見つけ続けたからです。

最も有用なリソースの短いリストを次に示します。

また、グラフを作成するには、データを含む多くのテーブルを処理する必要がありました。

ロンドン大学色と視覚研究所データベース（XYZカラーマッチング機能、コーンの基本）
fluxometer.com（LCD上のRGBサブピクセルの範囲）
CIE 15：テクニカルレポート：測色、第3版（RGBカラーマッチング機能）

この記事の草案に関する貴重なフィードバックをいただいたChris CooperとRyan Kaplanに感謝します。

色：六角目