
サイクルからの記事:
フランシスはインペリアルカレッジロンドンを卒業し、コンピューターテクノロジーの学位を取得しています。 彼女はMicrosoft Researchで働いている間に卒業プロジェクトを書きました。 Francesは現在、マイクロソフトでソフトウェアエンジニアとして働いています。 彼女の活動の主な分野は、機械学習、ビッグデータ、量子コンピューティングです。
記事の内容
- 基本を繰り返す
- 量子ビットを測定する
- 量子バルブ
- 重要なバルブ
- 少数のキュービット
- 別の重要なバルブ
- ベルの状態
- 量子プログラムを書く
- 次は?
- アプリ
- 追加資料
基本を繰り返す
最下位レベルでプログラミングしない場合、実際には、「クラシック」コンピューターに保存されているゼロと1だけを操作するプログラムを忘れてしまう可能性があります。 これらのゼロと1は、物理システムの離散的なバイナリ状態に対応します。 量子コンピューターは、連続した状態範囲で動作します。 部分的にそれらの機能はこれによるものです。
クラシックビットは、通常の白熱灯のように、「オン」または「オフ」の2つの状態のいずれかのみを取ります。 量子コンピューターの基礎であるキュービットは、調光可能なランプに似ています。

量子ビットの2つの状態を記録するには、braとket(Dirac表記)という表記法を使用できます。これらの表記法は、次のベクトルに対応しています。
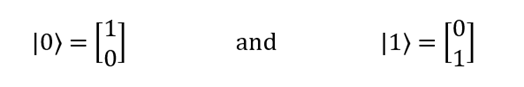
これら2つの状態の線形結合を使用して、ベクトル| 0〉と| 1〉の可能な組み合わせを表現できます。 量子力学では、このような組み合わせは重ね合わせと呼ばれます。 ディラックの表記の対応するエントリは次のようになります。
|ψ⟩=α| 0〉 +β| 1〉
αとβの値は確率に関連しています(わずかな違いがあります-これらの係数は複素数で表現できます)。 それらは実数と考えることができますが、この場合、負の値をとることができることを覚えておいてください。 ただし、それらの平方の合計は常に1です。
量子ビットを測定する
量子状態は奇妙なものです。 測定の結果(または、彼らが言うように、「オブザーバーの存在下で」)、キュービットはすぐに崩壊します。 これを理解する方法は? 量子ビットが重ね合わせ状態にあるとします。 それを測定する場合、1つの特定の値を取ります-| 0〉または| 1〉(両方の測定で一度に両方の結果を示すことはできません!) 量子ビットを測定した後、以前の状態を特徴付けた係数αとβは、実際には失われます。
したがって、確率理論装置を使用して、キュービットの測定値を記述します。 一般的な場合、キュビットの状態を測定すると結果が表示される確率| 0〉は次と等しくなります。
 、状態を取得する確率| 1〉は
、状態を取得する確率| 1〉は 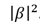 。 例を考えてみましょう。 次のキュービットがあるとします:
。 例を考えてみましょう。 次のキュービットがあるとします:
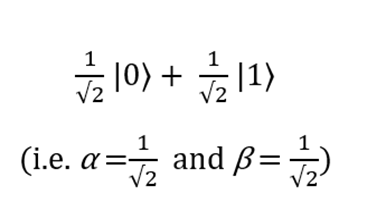
その状態を測定すると、ケースの50%で値0が得られます。
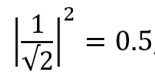
つまり、測定後の状態は| 0〉(つまり、α= 1、β= 0)になります。 同じ理由で、状態1になる確率は50%です。 この場合、測定後、キュービットは状態| 1〉になります(つまり、α= 0、β= 1)。

初めて、これはすべて非常に混乱します(2回目、3回目、および4回目は、何も変わりません)。 ここでの主な考え方は、確率論的な量子状態を計算に使用できることであり、場合によっては、それらの量子「ストレンジネス」により、従来のものよりも高い効率のシステムを得ることができます。 では、これらのキュービットを、古典的なビットのように計算に使用する方法を見てみましょう。
量子バルブ
もっと身近なものに戻りましょう。 古典的な計算理論では、論理ゲートを使用してビットの演算を実行します。 量子ビットを操作するために、同様の設計-量子ゲートが使用されます。 たとえば、NOTゲートは0→1および1→0の変換を実行します。量子NOTゲートはその古典的な祖先に似ています。変換| 0>→| 1〉および| 1〉→| 0〉を実行します。 これは、そのようなゲートを通過した後、状態α| 0〉 +β| 1〉からのキュービットが状態α| 1〉 +β| 0〉になることを意味します。 NOTゲートは、状態マトリックスの0と1を交換するマトリックス(X)として記述できます。
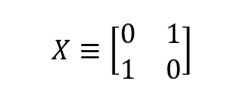
ご覧のとおり、X | 0〉 = | 1〉、X | 1〉 = | 0〉:
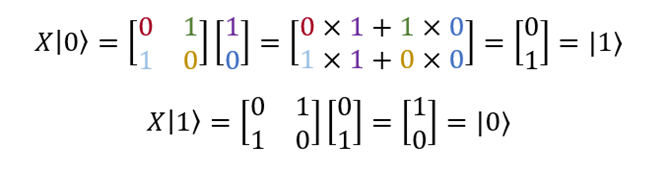
ベクトル形式の| 0〉および| 1〉は、
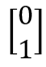 そして
そして  、行列Xの最初の列はベクトルの変換と見なすことができます| 0〉、2番目の-はベクトルの変換と見なします| 1〉。
、行列Xの最初の列はベクトルの変換と見なすことができます| 0〉、2番目の-はベクトルの変換と見なします| 1〉。
古典的な場合との違いはそれほど大きくないようです。 ただし、前のセクションで説明したことを忘れないでください。キュービットの状態の測定は確率的です。 初等確率理論から知られているように、互換性のないイベントの完全なグループの確率の合計は1です。 だから
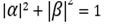 量子状態の場合、α| 0〉 +β| 1〉。
量子状態の場合、α| 0〉 +β| 1〉。
したがって、考えられるすべてのゲートが量子世界に存在するとは限りません。 制限の1つは次のとおりです。キュービットの量子状態を正規化する条件、
 、バルブの通過前と通過後の両方で観察する必要があります。 行列代数に関しては、行列がユニタリの場合、この条件は満たされます。
、バルブの通過前と通過後の両方で観察する必要があります。 行列代数に関しては、行列がユニタリの場合、この条件は満たされます。
ユニタリティの数学的概念が何を意味するかを説明しようとします。 十分に速く読めば、次の文章に簡単に出会えます。 バルブは、ユニタリと呼ばれます
 転置と複素共役によって得られる
転置と複素共役によって得られる  これはランク2の単位行列です。人間の言語で言えば、これは変換がベクトルの長さを変更しないことを意味します。 ベクトルの長さが時間とともに変化しない場合、すべての確率の合計は常にユニティまたは100%(あるべき)に等しくなります。 その結果、すべての確率の合計が200%または25%に等しい計算は無意味になります。 ユニタリ行列は、少なくともそのような狂気から保護します(ただし、量子世界では豊富なままです)。
これはランク2の単位行列です。人間の言語で言えば、これは変換がベクトルの長さを変更しないことを意味します。 ベクトルの長さが時間とともに変化しない場合、すべての確率の合計は常にユニティまたは100%(あるべき)に等しくなります。 その結果、すべての確率の合計が200%または25%に等しい計算は無意味になります。 ユニタリ行列は、少なくともそのような狂気から保護します(ただし、量子世界では豊富なままです)。
良いニュース:この制限は唯一のものです。 この条件により、一部の古典的なゲートには量子アナログがありませんが、一部の量子ゲートには古典的なプロトタイプがありません。 次に、最も重要な量子ゲートを分析します。
重要なバルブ:バルブZおよびアダマールバルブ
以下で説明するゲートは、最初の量子プログラムで使用されるので、覚えておいてください。 ゲートZは非常に簡単に機能します。コンポーネント| 0〉を保存し、コンポーネントの符号を変更します| 1〉。 行列として書くことができます

量子ビット状態を次のように変換します:| 0〉→| 0〉、| 1〉→-| 1〉(行列の最初の列はベクトルの変換を表すことに注意してください| 0〉、2番目-ベクトルの変換| 1〉)。
アダマールバルブは、上記と同様の状態| 0〉と| 1〉の重ね合わせを作成します。 彼のマトリックスエントリは次のようになります。
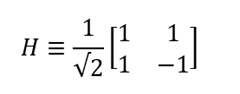
次の量子ビット状態の変換に対応します。
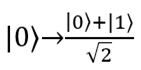 、
、 
ユニタリマトリックスおよびゲートの視覚的表現の方法に関する詳細情報は、「追加資料」セクションに含まれるリソースに記載されています。
少ない量子ビット
もっと身近なものを考えてください。 古典的なビットは、1つずつだけでなく、組み合わせの形式(たとえば、00、01、10、11)でも存在します。量子計算では、同様の組み合わせが使用されます:| 00〉、| 01〉、| 10〉、および11〉。 2つのキュービットの状態は、次のベクトルを使用して説明できます。
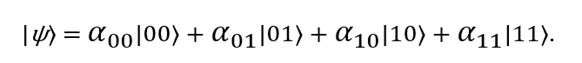
前と同様に、測定の結果として00になる確率は
 、
、
01の場合、確率は
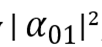 など
など
両方のキュービットではなく、最初のキュービットの状態を測定したいとします。 0になる確率は
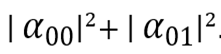 。 私たちが思い出すように、測定は状態を変えるので、その後はベクトルが重要になります
。 私たちが思い出すように、測定は状態を変えるので、その後はベクトルが重要になります

分子に注意してください。最初のビットが1であるすべての項を削除しました(条件により、測定結果は0であるため)。 ベクトルが許容可能な量子状態を記述するためには、振幅の合計の2乗が1に等しいことが必要です(変換の前と後の両方)。 この条件が満たされるように、正規化係数(行列式の平方根に逆の値)を追加します。
別の重要なバルブ
NOTバルブの操作はすでに分解されています。 次に続くのは、CNOT(制御-NOT)バルブです。 2つのキュービットがその入力に供給されます。 最初はマネージャーと呼ばれ、2番目は管理されます。 制御キュービットが| 0〉の場合、制御キュービットの状態は変化しません。 制御キュービットが| 1〉の場合、NOT演算が制御キュービットに適用されます。
CNOT操作はいくつかの方法で解釈できます。 バルブX、Z、Hと同様に、マトリックス形式で記述できます。これは文字Uで示されます。
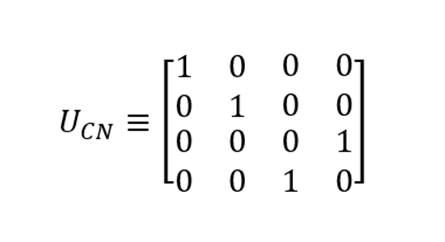
マトリックスの列が次の変換に対応していることがわかります:| 00〉→| 00〉、| 01〉→| 01〉、| 10〉→| 11〉、| 11〉→| 10〉。 分析したマトリックスのように
 、それはユニタリです、つまり
、それはユニタリです、つまり  。
。
次の指定もこのバルブに使用されます(上部は制御キュービットに対応し、下部は制御キュービットに対応します)。

現代美術展の展示のようです。
ベルの幸運
セクション全体をこの重要なトピックに当てる必要があります。 合計で4つのベル状態があります。 それらの1つ(| ϕ +⟩)は、以下の量子プログラムで使用されます。 それを見てみましょう。
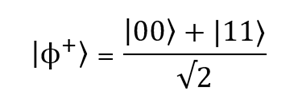
最初のキュービットの状態を測定するとします。 結果| 0〉確率で得る
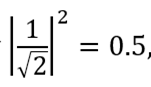 。 これは、同じ確率(0.5)で|ψ '⟩= | 00〉、または| 1〉を測定した後の状態、および|ψ'⟩= | 11〉を測定した後の状態を意味します。 好奇心のために、ベル状態の完全なセットを提示します(量子エンタングルメントの最も単純なケースです):
。 これは、同じ確率(0.5)で|ψ '⟩= | 00〉、または| 1〉を測定した後の状態、および|ψ'⟩= | 11〉を測定した後の状態を意味します。 好奇心のために、ベル状態の完全なセットを提示します(量子エンタングルメントの最も単純なケースです):

次に、2番目のキュービットの状態を測定したとします。 同じ理由によると、蒸気を測定した後の状態は| 00〉または| 11〉になります。 その後、最初のキュービットの状態を測定することにした場合、確率は0.5でなくなります。 測定結果が何であったかに応じて、1または0の確率で| 0〉を取得します。 これらの結果は関連していることを理解することが重要です。 これに最初に気づいたのは、アルバート・アインシュタイン、ボリス・ポドルスキー、ネイサン・ローゼンでした(したがって、これらの州は「EPRペア」と呼ばれることもあります)。 その後、彼らの理論はジョン・ベルによって開発されました。
最後に、アダマールバルブとCNOTバルブを使用してベル状態を生成できます。 私の意見では、これは立派です。 アダマール弁は、最初のキュービットを重ね合わせ状態にします。 この量子ビットは、CNOTバルブの制御入力に送られます。 以下に、回路図を使用してこのプロセスを表す方法を示します。
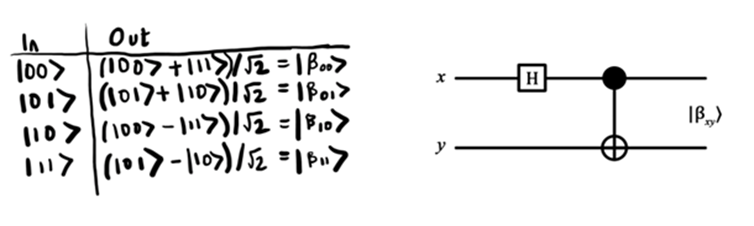
これらの各変換がどのように機能するかの詳細については、追加の資料を参照してください(リストは以下のとおりです)。 量子ビット状態、量子ゲート、ベル状態については、最初の量子ビットプログラムを書くのに十分な知識があります。
量子プログラムを書く
ドキュメントの指示に従います 。
このチュートリアルは、次の手順を実行するのに役立ちます。量子プログラム開発パッケージをインストールし(手順1〜2)、量子ビットを選択していくつかの簡単な操作を実行します。たとえば、特定の状態に設定して測定し(手順3〜5)、翻訳します量子ビットを重ね合わせ状態に変換し(ステップ6)、2つの量子ビットをもつれ状態(ベル状態、またはEPRのペア)に変換します(ステップ7)。
上記のマニュアルの指示に従い、ヒントや追加の説明が必要な場合はこの資料に戻ることをお勧めします。
ステージ1.プロジェクトの作成とソリューション
Q#はこのリストの一番下にあります。

ステージ2(オプション)。 NuGetパッケージの更新
このアドバイスに従いましたが、特にリスクを冒したい場合は、これは必要ありません。
ステップ3. Q#コードを入力します
namespace Quantum.Bell { open Microsoft.Quantum.Primitive; open Microsoft.Quantum.Canon; operation Set (desired: Result, q1: Qubit) : () { body { let current = M(q1); if (desired != current) { X(q1); } } } }
この操作はキュービットを状態(私たちが選択)-0または1に転送します。最初にキュービットを測定し(この操作は文字Mで示されます)、状態0または1に折りたたまれます。 NOT、X。そうでなければ、何もする必要はありません。
operation BellTest (count : Int, initial: Result) : (Int,Int) { body { mutable numOnes = 0; using (qubits = Qubit[1]) { for (test in 1..count) { Set (initial, qubits[0]); let res = M (qubits[0]); // Count the number of ones we saw: if (res == One) { set numOnes = numOnes + 1; } } Set(Zero, qubits[0]); } // Return number of times we saw a |0> and number of times we saw a |1> return (count-numOnes, numOnes); } }
この小さなコードは、先ほど書いた操作をテストするために設計されています。 これは非常に単純なプログラムです。キュービットが必要な状態に転送されたことを確認します。
これを行うために、彼女はループで測定を行い、変数numOnesを使用して結果1の数をカウントします。
「Qubit [1]」という表記は、「1つの要素からキュービットの配列を作成する」ことを意味します。 配列要素のインデックス付けはゼロからです。 2つのキュービットを区別するには(後でこれを行う必要があります)、「Qubit [2]」と書く必要があります。 このような配列のキュービットは、番号0と1に対応します。
forループでは、特定の初期状態に割り当てられたキュービットをOneまたはZeroに設定します( Driver.csファイルで、すぐに取得しますが、これは明示的に行われます)。 この状態を測定し、1の場合、カウンター値を1増やします。 この関数は、1と0の観測された状態の数を返します。 最後に、キュービットはゼロ状態になります(既知の状態のままにするため)。
ステップ4. C#ドライバーコードの入力
using (var sim = new QuantumSimulator()) { // Try initial values Result[] initials = new Result[] { Result.Zero, Result.One }; foreach (Result initial in initials) { var res = BellTest.Run(sim, 1000, initial).Result; var (numZeros, numOnes) = res; System.Console.WriteLine( $"Init:{initial,-4} 0s={numZeros,-4} 1s={numOnes,-4}"); } } System.Console.WriteLine("Press any key to continue..."); System.Console.ReadKey();
このドライバーは、量子シミュレーターとチェックする初期値の配列(ゼロと1)を作成します。 次に、シミュレーションが1000回繰り返され、デバッグの結果がSystem.Console.WriteLine関数を使用して表示されます。
ステージ5.アセンブリと実装
Init:Zero 0s=1000 1s=0
Init:One 0s=0 1s=1000
Press any key to continue...
すべてが正常な場合、画面の出力は上記のようになります。 この結果は、初期キュービットをゼロ状態に転送し、1000回の繰り返しを実行すると、観測結果に応じた状態の数| 0〉は1000になることを意味します。1つの状態についても同様です。
ステップ6.重ね合わせの作成
もっと面白いものを試してみましょう。 ここで、NOTゲートを使用してキュービットの状態を変更します。
X(qubits[0]); let res = M (qubits[0]);
次に、プログラムを再度実行し、結果が逆になることを確認します。
Init:Zero 0s=0 1s=1000
Init:One 0s=1000 1s=0
次に、NOTバルブをアダマールバルブ(H)に交換します。 その結果、私たちが知っているように、キュービットは状態の重ね合わせになり、その測定結果は確率で| 0〉と| 1〉に等しくなります。
H(qubits[0]); let res = M (qubits[0]);
プログラムを再度実行すると、かなり興味深い結果が得られます。
Init:Zero 0s=484 1s=516
Init:One 0s=522 1s=478
測定の数| 0〉と| 1〉はほぼ等しくなります。
ステップ7.もつれた状態の準備
次に、ベル状態を作成します。 以下のコードをご覧ください。 まず、2つのキュービットの配列を作成します(Qubit [2])。 最初のキュービット(回路の前の図ではシンボルxで示されていました)を何らかの初期状態に変換し、2番目(図のy)をゼロに設定します。 これは、Xに応じて| 00〉または| 10〉を入力するのとほぼ同じです。
operation BellTest (count : Int, initial: Result) : (Int,Int) { body { mutable numOnes = 0; using (qubits = Qubit[2]) { for (test in 1..count) { Set (initial, qubits[0]); Set (Zero, qubits[1]); H(qubits[0]); CNOT(qubits[0],qubits[1]); let res = M (qubits[0]); // Count the number of ones we saw: if (res == One) { set numOnes = numOnes + 1; } } Set(Zero, qubits[0]); Set(Zero, qubits[1]); } // Return number of times we saw a |0> and number of times we saw a |1> return (count-numOnes, numOnes); } }
図によると、最初のキュービットであるキュービット[0]は、アダマール弁を通過する必要があります。 その結果、彼は重ね合わせになります。 次に、CNOTバルブにキュービットを渡し(キュービット[0]-制御キュービット、キュービット[1]-制御)、結果を測定します。
結果が予想されるものを理解するために、ベル状態がどのように機能するかをもう一度繰り返しましょう。 最初のキュービットを測定すると、確率| 0〉が得られます
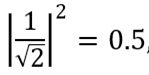 。 これは、同じ確率(0.5)で|ψ '⟩= | 00〉または| 1〉を測定した後の状態、および|ψ'⟩= | 11〉を測定した後の状態を意味します。 したがって、2番目のキュービットの状態を測定した結果は、最初のキュービットが状態| 0〉にある場合は| 0〉、最初のキュービットが状態| 1〉にある場合は| 1〉になります。 2つのキュービットの状態がうまく混同された場合、結果は、最初と2番目のキュービットが同じ状態にあることを示すはずです。
。 これは、同じ確率(0.5)で|ψ '⟩= | 00〉または| 1〉を測定した後の状態、および|ψ'⟩= | 11〉を測定した後の状態を意味します。 したがって、2番目のキュービットの状態を測定した結果は、最初のキュービットが状態| 0〉にある場合は| 0〉、最初のキュービットが状態| 1〉にある場合は| 1〉になります。 2つのキュービットの状態がうまく混同された場合、結果は、最初と2番目のキュービットが同じ状態にあることを示すはずです。
コードでは、ifステートメントを使用して、量子ビット[1]の測定結果が量子ビット[0]の測定結果と等しいかどうかを確認します。
operation BellTest (count : Int, initial: Result) : (Int,Int,Int) { body { mutable numOnes = 0; mutable agree = 0; using (qubits = Qubit[2]) { for (test in 1..count) { Set (initial, qubits[0]); Set (Zero, qubits[1]); H(qubits[0]); CNOT(qubits[0],qubits[1]); let res = M (qubits[0]); if (M (qubits[1]) == res) { set agree = agree + 1; } // Count the number of ones we saw: if (res == One) { set numOnes = numOnes + 1; } } Set(Zero, qubits[0]); Set(Zero, qubits[1]); } // Return number of times we saw a |0> and number of times we saw a |1> return (count-numOnes, numOnes, agree); } }
結果を確認する前に、Driver.csファイルにもう1つ変更を加える必要があります。agree変数を追加します。
using (var sim = new QuantumSimulator()) { // Try initial values Result[] initials = new Result[] { Result.Zero, Result.One }; foreach (Result initial in initials) { var res = BellTest.Run(sim, 1000, initial).Result; var (numZeros, numOnes, agree) = res; System.Console.WriteLine( $"Init:{initial,-4} 0s={numZeros,-4} 1s={numOnes,-4} agree={agree,-4}"); } } System.Console.WriteLine("Press any key to continue..."); System.Console.ReadKey();
これで、プログラムを起動できます。 これらの結果はどういう意味ですか? 最初のキュービットが最初にゼロ状態になった場合(つまり、値| 00〉を入力した場合)、アダマールバルブはキュービットを重ね合わせ状態にし、測定結果は50%の場合は0%、50%の場合は1%になります。 この条件が満たされるかどうかは、ゼロと1の数で推定できます。 最初のビットの状態の測定が2番目のビットの状態に影響しなかった場合、| 0〉に等しくなり、499の場合にのみ一貫性が達成されます。
しかし、ご覧のとおり、1番目と2番目のキュービットの状態は完全に一貫しています。結果の数| 0〉と| 1〉(ほぼ)は一致します。 したがって、結果は1000の各ケースで一貫しています。 それがベルの州の仕組みです。
Init:Zero 0s=499 1s=501 agree=1000
Init:One 0s=490 1s=510 agree=1000
これで終わります。 最初の量子プログラムを作成し、(最後まで到達したので)おそらくそれが何をしていたかを理解したでしょう。 お茶を一杯飲むのは注目に値します。

次は?
GitHubリポジトリには多くの例があります。
次の記事では、量子テレポーテーションの理論について説明し、コード例を検討します。
量子ゲートについては、Anitaのブログで詳しく説明しています(注:Anitaは最高です)。
追加資料
議論されているトピックを掘り下げたい場合、以下は私たちにとって非常に有用なリソースのリストです。 最初の本は「量子コンピューティングと量子情報」(M. Nielsen、I。Chang)です。 2つ目は、Microsoft SDKのドキュメントです。
これが読者にとって興味深い場合(コメントを残してください!)、他のリソースについての別の出版物を書くことができます。
アプリケーション。 ベルの幸運

ベル状態は、アダマールバルブとCNOTバルブを使用して生成できます。 アダマール弁は、最初のキュービットを重ね合わせ状態にします。 この量子ビットは、CNOTバルブの制御入力に送られます。 回路図では、次のようになります。
状態| 00〉のキュービットのペアが入力に供給される最初のケースから始めます。 最初のキュービット| 0〉は、アダマール弁を通過して、
 。 2番目のキュービットは変更されません。 結果:
。 2番目のキュービットは変更されません。 結果:
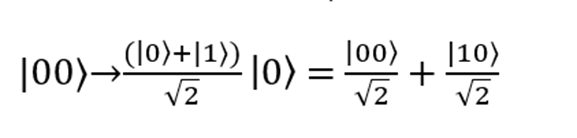
その後、キュービットはCNOTバルブを通過します(変換は| 00〉→| 00〉および| 10〉→| 11〉を実行します)。 今、彼らの状態は式で記述されます

2番目のケース:キュービット| 01〉が入力されます。 アダマールバルブは、最初のキュービット| 0〉を状態に転送します
 。 2番目のキュービットは変更されません。 結果:
。 2番目のキュービットは変更されません。 結果:
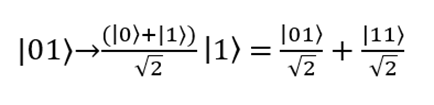
次に、量子ビットがCNOTゲートを通過するようにします。CNOTゲートは、変換| 01〉→| 01〉および| 11〉→| 10〉を実行します。 一対のキュービットの最終状態は次のようになります。

3番目のケース:キュービット| 10〉が入力に送られます。 アダマールゲートは最初のキュービット|1⟩を状態にする
 。 2番目のキュービットは変更されません。 結果:
。 2番目のキュービットは変更されません。 結果:

その後、キュービットはCNOTバルブを通過します(変換は| 00〉→| 00〉および| 10〉→| 11〉を実行します)。 今、彼らの状態は式で記述されます
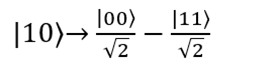
4番目のケース:キュービット| 11〉が入力されます。 アダマールゲートは最初のキュービット|1⟩を状態にする
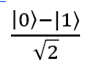 。 2番目のキュービットは変更されません。 結果:
。 2番目のキュービットは変更されません。 結果:

次に、量子ビットがCNOTゲートを通過するようにします。CNOTゲートは、変換| 01〉→| 01〉および| 11〉→| 10〉を実行します。 一対のキュービットの最終状態は次のようになります。

すべてのケースを整理しました。