浴室のモザイクとディオファントス方程式

寝る前の夕方だった。 私は歯を磨き、バスルームのモザイクを疲れて見た。 何らかの理由で、私はそのような単純な事実に興味がありました：2×3セルの長方形が両側のセルで囲まれている場合、ストロークの面積は長方形の面積と同じになります：

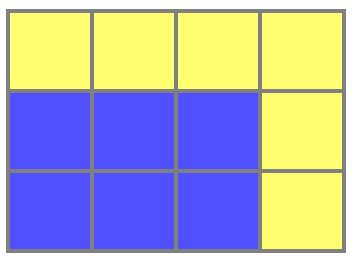
黄色の正方形と同じ数の青い正方形があります。 そして、私は苦しみました。

まだそのような構成があるのだろうかと思いました。 つまり、長方形を作る $$$a \ times b$ 両側に輪郭がある円で、輪郭の面積は長方形の面積と一致します。 もちろん $$$a$ そして $$$b$ 整数でなければなりません：

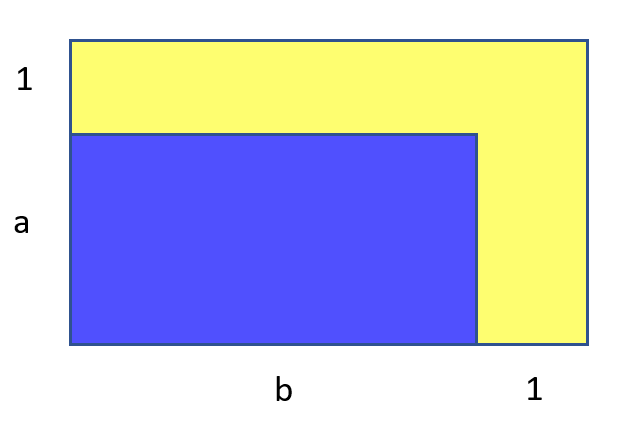
そのような場合はもうないはずです。 青い部分の面積 $$$a \ times b$ と黄色 $$$a + b + 1$ 。 それが見られることができる場合 $$$a$ または $$$b$ ユニットの場合、一致するものはありません。さらに増やすと $$$2 \回3$ その後、青は明らかに速く成長します。 したがって、この構成は1つです。

退屈だと脳は言った。 タスクを弱める必要があります。 これを言ってみましょう：

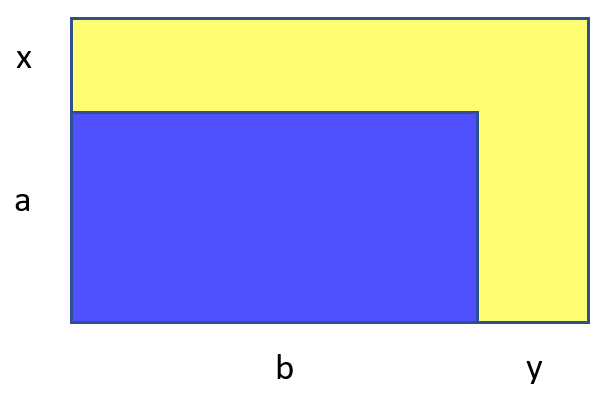
しかし、今はタスクが弱すぎます。 実際、整数の辺を持つ2つの長方形を選択して、それらの面積が半分だけ正確に異なるようにする必要があります。 そして、長方形の制限は、一方を他方に押し込めることだけです。 それらが多すぎて退屈すぎます。 これをやってみましょう：

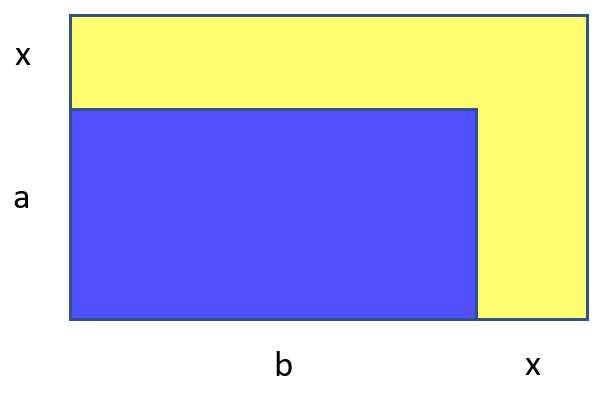
境界線の幅を修正します。 いくつありますか？ ふむ もっと面白そうです。 黄色の広場は $$$（x + a）（x + b）-ab$ 、そして私たちは彼女がちょうど等しくなることを望みます $$$ab$ 。 つまり、私（私とこれに引き込まれた私の脳）は方程式を解く必要があります：

$$

$$（x + a）（x + b）-ab = ab$$

または、同じこと：

$$

$$x ^ 2 + ax + bx-ab = 0$$

この時までに、私は歯で仕上げ、食器洗い機に粉を注ぎ始めました。 うん、脳は言った、悪くない挑戦。 もちろん、整数で解く必要があります。つまり、これはディオファントス方程式です。 私たちは大学でディオファントス方程式を経験しませんでしたが、人気のある記事からそれらについて何かを思い出しました。 すなわち：

• 均一な方程式があれば、幸運です。
• 整数の同次方程式を合理的な方程式に変換し、変数の数を1つ減らすのは簡単です。
• ピアリングの方法を使用して、有理数に関する二次方程式のルートを見つける場合、他のすべてを見つけるのは簡単です。
• 既知のルートを通過する有理係数を持つ直線は、別のルートを通過します。 この線をひねると、すべての有理根を取得できます。

このようにして、たとえば、すべてのピタゴラストリプルの一般式が簡単に見つかります。 ところで、ピタゴラスのトリプルと同様に、私たちの問題では、いくつもの解決策がいくつもあります。 たとえば、長方形 $$$4 \回6$ 2つの小さな正方形の境界線で拡大できます。 もちろん、私たちは複数のソリューションにのみ興味があります。

保湿剤を手に入れて、これをすべて自分の頭の中でできるようになると思いました。 一枚の紙とコンピューターのない代数はやや陰湿なものです。プラスとマイナスを混ぜたり、メンバーを忘れたりして、さらに計算が無駄になります。 プログラマーは、エラーの可能性を減らすために何をすべきかを知っています-ユニットテストに囲まれる必要があります。 幸いなことに、私たちはすでに1つのソリューションを知っています。 $$$x = 1; a = 2; b = 3$ 。 すべてのステップで確認します。

$$

$$1 ^ 2 + 2 \回1 + 3 \回1-2 \回3 = 0$$

これまでのところ、とても良い。 したがって、同次方程式があります-すべての項は2次に含まれます。 方程式を除算する $$$x ^ 2$ （ケース $$$x = 0$ 興味がないので、共有できます）：

$$

$$1 + \ frac a x + \ frac b x-\ frac a x \ times \ frac b x = 0$$

交換の作成： $$$p = a / x; q = b / x$ そして、2つの有理変数を含む方程式を取得します。

$$

$$1 + p + q-pq = 0$$

ユニットテストで $$$p = 2; q = 3$ 、テストに合格しました。 次に、直線を描く必要があります。 原則として、それはちょうど点を通して描くことができます $$$（2; 3）$ しかし、脳内に留めるのは難しいです。 しかし、ピアリングの方法により、方程式を満たす別のポイントを簡単に見つけることができます。 $$$p = -1; q = 0$ 。 これはゼロエリアに対応します $$$a \ times b$ 繰り返しになりますが、解決策としてはあまり面白くありませんが、直接的なものとしては適切です。 すべての行（1つを除く）が通過することに気付くのは非常に簡単です $$$p = -1; q = 0$ 明示的な方程式で記述されている $$$q = \ alpha（p + 1）$ （はい、何らかの理由で脳はギリシア文字を配りましたが、ラテン文字はまだ終わりませんでした）。 不足している行は $$$p = -1$ 彼女は私たちにとってあまり面白くない。 もちろん、合理的な点 $$$（p; q）$ どこで $$$p \ neq -1$ 一貫した合理的 $$$\ alpha$ 。 たとえば、ポイント $$$（2; 3）$ 価値 $$$\ alpha = 1$ 。 線の方程式を方程式に代入して、以下を取得します。

$$

$$1 + p + \ alpha（p + 1）-\ alpha p（p + 1）= 0$$

または

$$

$$1 + p + \ alpha p + \ alpha-\ alpha p ^ 2-\ alpha p = 0$$

または

$$

$$1 + p + \ alpha-\ alpha p ^ 2 = 0$$

または

$$

$$\ alpha p ^ 2-p-（1 + \ alpha）= 0$$

メンバーを頭に入れるのは難しくなります;脳は必死に一枚の紙を求めます。 しかし、私は赤ん坊を腕に抱きしめます。一枚の紙の時間はありません。 単体テストを実行します（ $$$p = 2; \ alpha = 1$ ）：

$$

$$1 \回2 ^ 2-2-（1 + 1）= 0$$

Fuf、これまでのところとても良い。 今、二次方程式があります $$$p$ これは、実際には合理的なルートを合理的に提供する必要があります $$$\ alpha$ 。 これはどのように判別できますか？ さて、試してみましょう：

$$

$$D = b ^ 2-4 a c = 1 ^ 2 + 4 \ alpha（1 + \ alpha）= 1 + 4 \ alpha + 4 \ alpha ^ 2 =（1 + 2 \ alpha）^ 2$$

まあ、まあ、完全な正方形が出てきました。 エンドルフィンは脳に行きました。 異常な常習者である彼はこれを求めたようです。 ここに数学の魔法があります。合理的な数が出てきて、出てきたはずです。 根の式を思い出してください：

$$

$$p_ {1,2} = \ frac {-b \ pm \ sqrt D} {2 a}$$

または表記法で：

$$

$$p_1 = \ frac {1-（1 + 2 \ alpha）} {2 \ alpha} = -1$$

$$

$$p_2 = \ frac {1 +（1 + 2 \ alpha）} {2 \ alpha} = \ frac {1 + \ alpha} \ alpha$$

$$$p_1$ 私たちの基準点です $$$-1$ 面白くないです 私たちのソリューションは $$$p_2$ 。 に置き換える $$$q = \ alpha（p + 1）$ 私たちは答えを得る：

$$

$$p = \ frac {1 + \ alpha} \ alpha; q = 1 + 2 \ alpha$$

つまり、すべての合理的な分数を次のように整理するだけです。 $$$\ alpha$ 、そしてそれらのために、方程式のすべての合理的な解を得る $$$1 + p + q-pq = 0$ （まあ、私たちにとってあまり面白くないものを除いて）。

もちろん、合理的な整数ではなく整数をソートする方が簡単です。 赤ちゃんにシメチコン製剤をはんだ付けし、私は代わりに $$$\ alpha = m / n$ 取得：

$$

$$p = \ frac {1 + \ frac m n} {\ frac m n} = \ frac {n + m} m$$

$$

$$q = 2 + \ frac m n = \ frac {n + 2m} n$$

（神、脳、なぜあなたは正確に選んだのですか $$$m$ そして $$$n$ ？ 彼らは頭でとても簡単に混乱しています！ 文字が少ないですか？）単体テストで、 $$$\ alpha = 1$ その後、フィット $$$m = n = 1$ そして、テストに合格することを確認するのは簡単です。

整数に戻す方法は？ 交換したことを忘れないでください $$$p = a / x; q = b / x$ 。 だから、私たちは $$$x$ 上記の式の共通分母の倍数である任意の数。 特に、ちょうど合う $$$mn$ 。 その結果、次のことができます。

$$

$$x = mn; a = mn + n ^ 2; b = mn + 2m ^ 2$$

それがわかることができます $$$m$ そして $$$n$ 相互に単純ではないため、解はそれらの公約数の倍数になるため、相互に単純なことにのみ関心がある $$$m$ そして $$$n$ 。 次の場合、複数の解も得られます $$$n$ 均等になります。 実際にしましょう $$$n = 2n '$ 。 それから

$$

$$x = 2mn '; a = 2mn '+ 4n' ^ 2; b = 2mn '+ 2m ^ 2$$

すべてを2つに分割すると、

$$

$$x = mn '; a = mn '+ 2n' ^ 2; b = mn '+ m ^ 2$$

この解決策は最初のものと対称的であり、非常に論理的です。問題は以下に関して対称的です。 $$$a$ そして $$$b$ 。 したがって、我々は相互にシンプルに興味があります $$$m$ そして $$$n$ 、そして $$$n$ 奇数。

便利なことに、 $$$x$ とても簡単でした。 したがって、指定されたエッジ幅のすべての非多重解を見つける簡単な方法があります $$$x$ ：これらはそのような長方形です $$$a = x + n ^ 2; b = x + 2（x / n）^ 2$ どこで $$$n$ 奇数の除数 $$$x$ と相互にシンプル $$$x / n$ 。 次の長方形は $$$x = 2; nは1です。 mは2です。 a = 3; b = 10$ ：

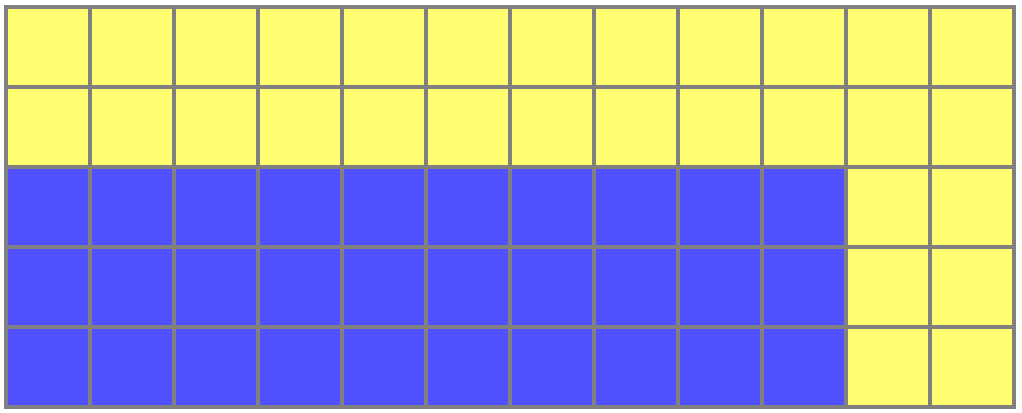
青と黄色の両方の部分には、正確に30個のセルが含まれています！

小さなもののための他のソリューションが何であるか見てみましょう。 $$$x$ （ $$$a$ そして $$$b$ 私は昇順で行くためにいくつかの場所で再配置しました）：

x	n	m	フリンジのない正方形	縁部
1	1	1	2×3 = 6	3×4 = 12
2	1	2	3×10 = 30	5×12 = 60
3	1	3	4×21 = 84	7×24 = 168
3	3	1	5×12 = 60	8×15 = 120
4	1	4	5×36 = 180	9×40 = 360
5	1	5	6×55 = 330	11×60 = 660
5	5	1	7×30 = 210	12×35 = 420
6	1	6	7×78 = 546	13×84 = 1092
6	3	2	14×15 = 210	20×21 = 420

頭の中でこれらの働きを数えることにより、脳は再びエンドルフィンの投与量を達成しました。 ある数字から別の数字へと、どれほど美しく素晴しい除数が流れるのか！ 例を挙げる $$$6 \回55$ ：1つ目は6で除算され、2つ目は11です。両方の数に5を加え、奇跡を加えます。1つ目は11で除算され、2つ目は6で除算されます。 そして、ここで、息子は落ち着いたように見えました。 夕方11時に、寝ることができます。

おそらく、これはすべて簡単に数えることができます。 おそらく私の推論はどこか不正確だった。 おそらく、これらの数字と作品には特別な名前が付いています。 私は知らない-見ていませんでした。 私はこれにもっと興味があります：私は私の意識を占有する唯一のナンセンスです、またはあなたもです 苦しむ 楽しんでいますか 彼らは私たちを治療しますか？