👩🏾‍✈️ 📩 🍨 ジニ係数。経済学から機械学習まで 💎 🏴󠁧󠁢󠁷󠁬󠁳󠁿 👆

興味深い事実：1912年、イタリアの統計学者であり人口統計学者であるCorrado Giniは、有名な作品「キャラクターの可変性と可変性」を書き、同じ年に「タイタニック」は大西洋に沈みました。これら2つのイベントの共通点は何でしょうか？単純で、その結果は機械学習の分野で広く使用されています。タイタニックデータセットに導入が必要ない場合は、イタリアの科学者の研究で最初に公開された1つの注目すべき統計についてさらに詳しく説明します。この記事は、分類問題のパーティションの品質の基準として決定木で使用されるGini不純物係数とは何の関係もないことにすぐに注意したいと思います。これらの係数は相互に関連するものではなく、ブリャンスク州のトラクターとオクラホマ州の芝刈り機の合計とほぼ同じ合計です。

Gini係数は、ターゲット変数のクラスの強い不均衡の条件下でのバイナリ分類問題の予測モデルの評価によく使用される品質メトリックです。銀行の融資、保険、およびターゲットを絞ったマーケティングのタスクで広く使用されているのはそれです。このメトリックを完全に理解するには、まず経済に突入して、そこで使用される理由を把握する必要があります。

経済学

ジニ係数は、先進的な市場経済を持つ国で使用されている経済的特徴（年収、財産、不動産）に対する社会の成層度の統計的指標です。基本的に、年間収入のレベルは計算された指標として採用されます。この係数は、社会における実際の収入の分布と、人口間の絶対的な均等分布との偏差を示し、社会における収入の不均一な分布を非常に正確に評価することができます。 1905年のジニ係数の誕生よりも少し前に、アメリカの経済学者マックス・ローレンツが「富の集中を測定する方法」という仕事で、後に「ローレンツ曲線」と呼ばれる社会の幸福の集中を測定する方法を提案したことは注目に値します。さらに、Gini係数はローレンツ曲線の絶対的に正確な代数的解釈であり、そのグラフィック表現であることがわかります。

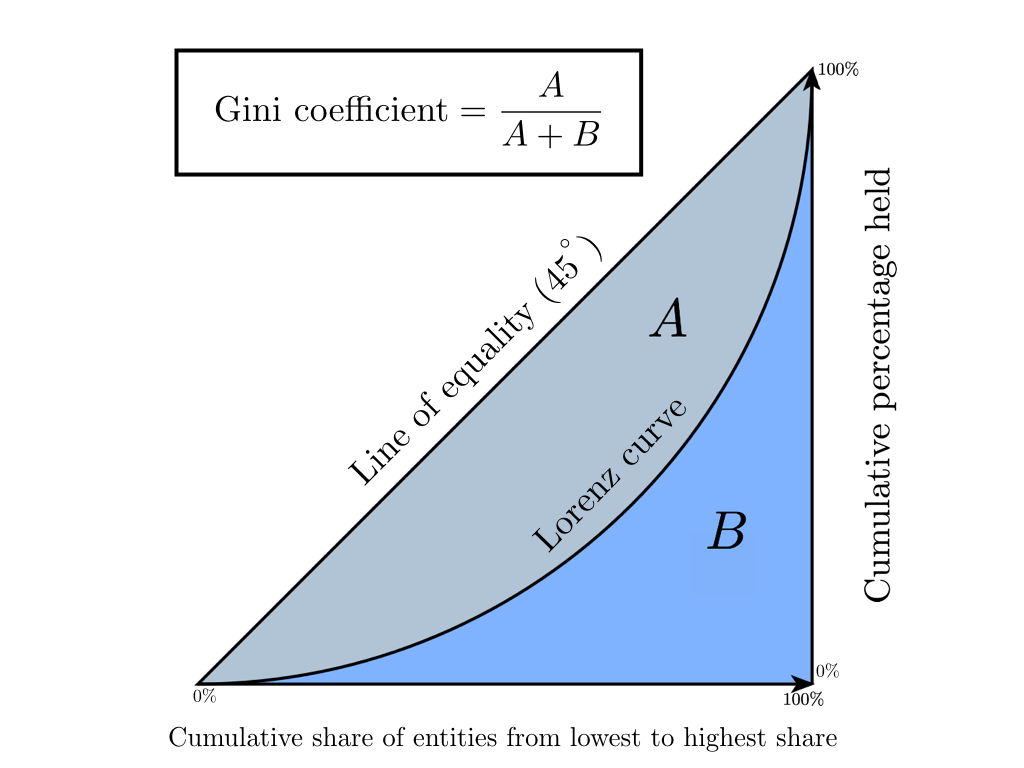
ローレンツ曲線は、各人口グループに帰属する総収入の割合をグラフで表したものです。グラフの対角線は「絶対平等線」に対応しています-人口全体の収入は同じです。

ジニ係数は0から1まで変化します。その値がゼロから外れて1に近づくほど、個々の人口グループの手に集中する収入が多くなり、州の社会的不平等のレベルが高くなります。時々、Giniインデックスと呼ばれるこの係数のパーセンテージ表現が使用されます（値は0％から100％まで変化します）。

経済学では、この係数を計算するいくつかの方法があります。ブラウンの式に焦点を当てます（最初にバリエーションシリーズを作成する必要があります-収入によって人口をランク付けするため）

（ ） （ ）

$G = 1-\ sum_ {k = 1} ^ n（X_k-X_ {k-1}）（Y_k + Y_ {k-1}）$

どこで

$n$ -住民の数

$X_k$ -人口の累積シェア、

$Y_k$ -収入の累積シェア

$X_k$

これらの統計の意味を直感的に理解するために、おもちゃの例で上記を見てみましょう。

3つの村があり、それぞれに10人の住民がいるとします。各村では、人口の年間総収入は100ルーブルです。最初の村では、すべての住民が同じ方法で収入を得ます-年に10ルーブル、2番目の村では収入の分配が異なります：3人が5ルーブル、4人が収入-10ルーブル、3人が15ルーブルです。そして、第3の村では、7人が1年に1ルーブル、1人-10ルーブル、1人-33ルーブル、1人-50ルーブルを受け取ります。各村について、ジニ係数を計算し、ローレンツ曲線を作成します。

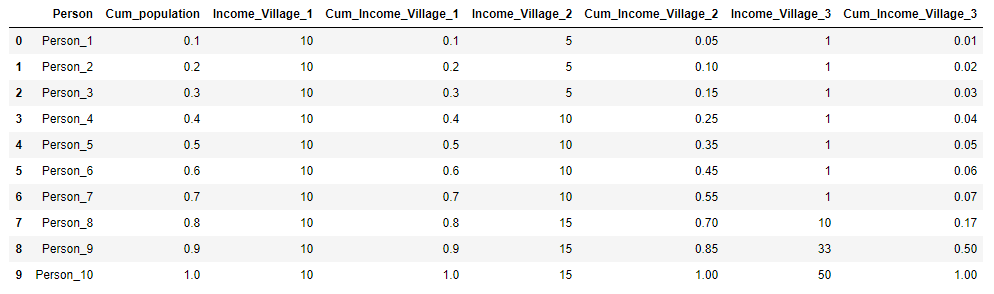
村の初期データを表形式で提示し、すぐに計算します

$X_k$ そして

$Y_k$ 明確にするために：

Pythonコード

import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline import warnings warnings.filterwarnings('ignore') village = pd.DataFrame({'Person':['Person_{}'.format(i) for i in range(1,11)], 'Income_Village_1':[10]*10, 'Income_Village_2':[5,5,5,10,10,10,10,15,15,15], 'Income_Village_3':[1,1,1,1,1,1,1,10,33,50]}) village['Cum_population'] = np.cumsum(np.ones(10)/10) village['Cum_Income_Village_1'] = np.cumsum(village['Income_Village_1']/100) village['Cum_Income_Village_2'] = np.cumsum(village['Income_Village_2']/100) village['Cum_Income_Village_3'] = np.cumsum(village['Income_Village_3']/100) village = village.iloc[:, [3,4,0,5,1,6,2,7]] village

Pythonコード

 plt.figure(figsize = (8,8)) Gini=[] for i in range(1,4): X_k = village['Cum_population'].values X_k_1 = village['Cum_population'].shift().fillna(0).values Y_k = village['Cum_Income_Village_{}'.format(i)].values Y_k_1 = village['Cum_Income_Village_{}'.format(i)].shift().fillna(0).values Gini.append(1 - np.sum((X_k - X_k_1) * (Y_k + Y_k_1))) plt.plot(np.insert(X_k,0,0), np.insert(village['Cum_Income_Village_{}'.format(i)].values,0,0), label=' {} (Gini = {:0.2f})'.format(i, Gini[i-1])) plt.title(' ') plt.xlabel('  ') plt.ylabel('  ') plt.legend(loc="upper left") plt.xlim(0, 1) plt.ylim(0, 1) plt.show()

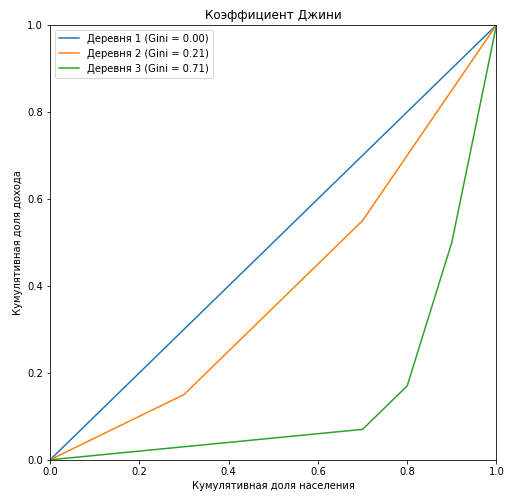
最初の村のジニ係数のローレンツ曲線は、対角線（「絶対平等線」）と完全に一致しており、年収に対する人口の層別化が大きいほど、ローレンツ曲線と対角線によって形成される図の面積が大きくなることがわかります。 3番目の村の例では、この図の面積と絶対等値線によって形成される三角形の面積の比がジニ係数の値と正確に等しいことを示しています。

Pythonコード

 curve_area = np.trapz(np.insert(village['Cum_Income_Village_3'].values,0,0), np.insert(village['Cum_population'].values,0,0)) S = (0.5 - curve_area) / 0.5 plt.figure(figsize = (8,8)) plt.plot([0,1],[0,1],linestyle = '--',lw = 2,color = 'black') plt.plot(np.insert(village['Cum_population'].values,0,0), np.insert(village['Cum_Income_Village_3'].values,0,0), label=' {} (Gini = {:0.2f})'.format(i, Gini[i-1]),lw = 2,color = 'green') plt.fill_between(np.insert(X_k,0,0), np.insert(X_k,0,0), y2=np.insert(village['Cum_Income_Village_3'].values,0,0), alpha=0.5) plt.text(0.45,0.27,'S = {:0.2f}'.format(S),fontsize = 28) plt.title(' ') plt.xlabel('  ') plt.ylabel('  ') plt.legend(loc="upper left") plt.xlim(0, 1) plt.ylim(0, 1) plt.show()

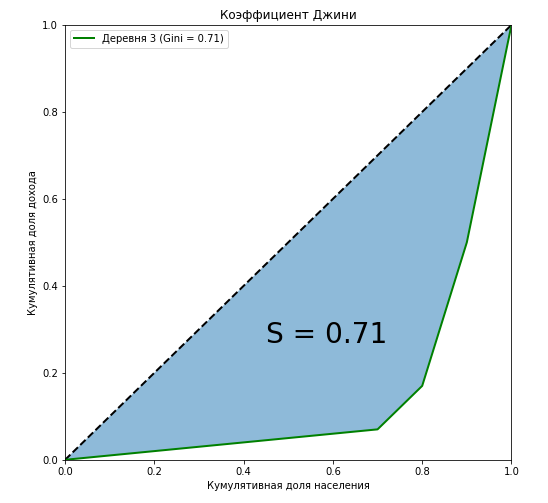
代数的手法とともに、Gini係数を計算する方法の1つは幾何学的であることが示されています-ローレンツ曲線と所得の絶対絶対平等線下の総面積から所得の絶対平等線までの面積割合を計算します。

もう一つの重要なポイント。ポイントで曲線の端を精神的に修正しましょう

（ ）

$（0,0）$ そして

（ ）

$（1,1）$ そしてその形を変え始めます。数字の大きさが変わらないことは明らかですが、そうすることで、階級間の収入の比率を変えることなく、社会の構成員を「中流階級」から貧困層または富裕層に移します。たとえば、次の収入を持つ10人を例に挙げます。

、 、 、 、 、 、 、 、 、 、

$[1、1、1、1、1、1、1、1、1、20、72]$

次に、Sharikovの「Select and Share！」メソッドを収入が「20」の人に適用し、社会の他のメンバー間で収入を比例配分します。この場合、Gini係数は変わらず、0.772のままです。単純に「固定」ローレンツ曲線を横軸に引いて、その形状を変更しました。

、 、 、 、 、 、 、 、 、

$[1 + 11.1 / 20、1 + 11.1 / 20、1 + 11.1 / 20、1 + 11.1 / 20、\\ 1 + 11.1 / 20、1 + 11.1 / 20、1 + 11.1 / 20、1 + 11.1 / 20、1 + 11.1 / 20、72 + 8.9 / 20]$

もう1つの重要な点について考えてみましょう。Gini係数を計算するとき、私たちは人々を金持ちと貧乏人に分類せず、貧乏人またはオリガルヒと考える人に依存しません。しかし、私たちがそのような課題に直面したと仮定します。そのために、私たちが得たいもの、私たちの目標に応じて、人々を金持ちと貧乏人に明確に分ける収入の閾値を設定する必要があります。これで、バイナリ分類問題からのしきい値との類推を見たなら、機械学習に移りましょう。

機械学習

1.一般的な理解

機械学習に来て、Gini係数は大きく変化していることに注意する必要があります。異なる方法で計算され、異なる意味を持っています。係数は、絶対等値線とローレンツ曲線によって形成される図の面積に数値的に等しくなります。また、経済からの相対的な共通の特徴もあります。たとえば、ローレンツ曲線を作成し、数字の面積を計算する必要があります。そして最も重要なことは、曲線を作成するためのアルゴリズムが変更されていないことです。ローレンツ曲線も変化しました。これはリフト曲線と呼ばれ、絶対等値線に対するローレンツ曲線の鏡像です（確率のランキングは増加しないが減少するため）。次のおもちゃの例でこれらすべてを分析します。図形の面積を計算する際のエラーを最小限に抑えるために、関数scipy interp1d （1次元関数の補間）およびquad （特定の積分の計算）を使用します。

15個のオブジェクトのバイナリ分類問題を解決し、次のクラス分布があるとします。

、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、

$[1、1、1、1、1、1、0、0、0、0、0、0、0、0、0、0、0]$

訓練されたアルゴリズムは、これらのオブジェクトのクラス「1」との関係の次の確率を予測します。

2つのモデルのGini係数を計算します：訓練されたアルゴリズムと、100％の確率でクラスを正確に予測する理想的なモデルです。考え方は次のとおりです。人口を収入でランク付けする代わりに、モデルの予測確率を降順にランク付けし、式の予測確率に対応するターゲット変数の真の値の累積割合を代入します。言い換えれば、テーブルを「予測」の行でソートし、収入の累積シェアではなく、クラスの累積シェアを考慮します。

Pythonコード

 from scipy.interpolate import interp1d from scipy.integrate import quad actual = [1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0] predict = [0.9, 0.3, 0.8, 0.75, 0.65, 0.6, 0.78, 0.7, 0.05, 0.4, 0.4, 0.05, 0.5, 0.1, 0.1] data = zip(actual, predict) sorted_data = sorted(data, key=lambda d: d[1], reverse=True) sorted_actual = [d[0] for d in sorted_data] cumulative_actual = np.cumsum(sorted_actual) / sum(actual) cumulative_index = np.arange(1, len(cumulative_actual)+1) / len(predict) cumulative_actual_perfect = np.cumsum(sorted(actual, reverse=True)) / sum(actual) x_values = [0] + list(cumulative_index) y_values = [0] + list(cumulative_actual) y_values_perfect = [0] + list(cumulative_actual_perfect) f1, f2 = interp1d(x_values, y_values), interp1d(x_values, y_values_perfect) S_pred = quad(f1, 0, 1, points=x_values)[0] - 0.5 S_actual = quad(f2, 0, 1, points=x_values)[0] - 0.5 fig, ax = plt.subplots(nrows=1,ncols=2, sharey=True, figsize=(14, 7)) ax[0].plot(x_values, y_values, lw = 2, color = 'blue', marker='x') ax[0].fill_between(x_values, x_values, y_values, color = 'blue', alpha=0.1) ax[0].text(0.4,0.2,'S = {:0.4f}'.format(S_pred),fontsize = 28) ax[1].plot(x_values, y_values_perfect, lw = 2, color = 'green', marker='x') ax[1].fill_between(x_values, x_values, y_values_perfect, color = 'green', alpha=0.1) ax[1].text(0.4,0.2,'S = {:0.4f}'.format(S_actual),fontsize = 28) for i in range(2): ax[i].plot([0,1],[0,1],linestyle = '--',lw = 2,color = 'black') ax[i].set(title=' ', xlabel='  ', ylabel='   ', xlim=(0, 1), ylim=(0, 1)) plt.show();

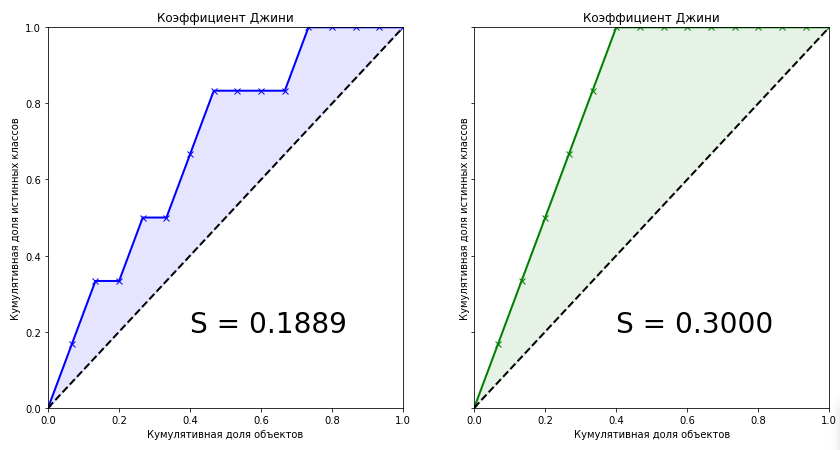
学習済みモデルのジニ係数は0.1889です。それは少しですか、それともたくさんですか？アルゴリズムはどれくらい正確ですか？理想的なアルゴリズムの係数の正確な値がわからなければ、モデルについて何も言えません。したがって、機械学習の品質メトリックは、 正規化されたGini係数であり、これは、訓練されたモデルの係数と理想モデルの係数の比に等しくなります。さらに、「ジニ係数」という用語では、まさにこれを意味します。

（ ）

$Gini_ {normalized} = \ frac {Gini_ {model}} {Gini_ {perfect}}（1）$

これらの2つのグラフを見ると、次の結論を導き出すことができます。

理想的なアルゴリズムの予測は、現在のデータセットの最大Gini係数であり、問題のクラスの真の分布のみに依存します。
理想的なアルゴリズムの図の領域は次のとおりです。

$エンスペースオブジェクトの数クラスのエンスペースエンスペースエンスペースのエンスペース選択$
$S = \ frac {\エンスペースオブジェクトの数\クラスのエンスペース\エンスペース0 \エンスペースの\エンスペース選択} {2}$
訓練されたモデルの予測は、理想的なアルゴリズムの係数値を超えることはできません。
ターゲット変数のクラスが均一に分布している場合、理想的なアルゴリズムのジニ係数は常に0.25になります
理想的なアルゴリズムの場合、リフト曲線と絶対等値線によって形成される図形の形状は常に三角形になります
ランダムアルゴリズムのジニ係数は0で、リフト曲線は絶対等値線と一致します
訓練されたアルゴリズムのジニ係数は、常に理想的なアルゴリズムの係数よりも小さくなります
訓練されたアルゴリズムの正規化されたジニ係数の値は、範囲内にあります $[0、1]$ 。
正規化されたGini係数は、最大化する必要がある品質メトリックです。

2.代数表現。 AUC ROCとの線形関係の証明

最も興味深い、おそらく最も興味深い瞬間、つまりジニ係数の代数的表現に至ります。このメトリックの計算方法は？彼女は経済からの彼女の親類と等しくありません。係数は次の式で計算できることが知られています。

$Gini_ {normalized} = 2 * AUCROC-1 \ hspace {15pt}（2）$

私はこの公式の結論をインターネットで見つけようとしましたが、何も見つかりませんでした。外国の本や科学記事でも。しかし、統計学者の疑わしいWebサイトでは、このフレーズが出てきました。 リフトカーブとROCカーブのグラフを比較するだけで、すべてが一目瞭然になります。」少し後に、彼自身がこれら2つのメトリックの接続の公式を導き出したとき、このフレーズが優れた指標であることに気付きました。あなたがそれを聞いたり読んだ場合、そのフレーズの作者がジニ係数を理解していないことは明らかです。この例のリフト曲線とROC曲線のグラフを見てみましょう。

Pythonコード

 from sklearn.metrics import roc_curve, roc_auc_score aucroc = roc_auc_score(actual, predict) gini = 2*roc_auc_score(actual, predict)-1 fpr, tpr, t = roc_curve(actual, predict) fig, ax = plt.subplots(nrows=1,ncols=3, sharey=True, figsize=(15, 5)) fig.suptitle('Gini = 2 * AUCROC - 1 = {:0.2f}\n\n'.format(gini),fontsize = 18, fontweight='bold') ax[0].plot([0]+fpr.tolist(), [0]+tpr.tolist(), lw = 2, color = 'red') ax[0].fill_between([0]+fpr.tolist(), [0]+tpr.tolist(), color = 'red', alpha=0.1) ax[0].text(0.4,0.2,'S = {:0.2f}'.format(aucroc),fontsize = 28) ax[1].plot(x_values, y_values, lw = 2, color = 'blue') ax[1].fill_between(x_values, x_values, y_values, color = 'blue', alpha=0.1) ax[1].text(0.4,0.2,'S = {:0.2f}'.format(S_pred),fontsize = 28) ax[2].plot(x_values, y_values_perfect, lw = 2, color = 'green') ax[2].fill_between(x_values, x_values, y_values_perfect, color = 'green', alpha=0.1) ax[2].text(0.4,0.2,'S = {:0.2f}'.format(S_actual),fontsize = 28) ax[0].set(title='ROC-AUC', xlabel='False Positive Rate', ylabel='True Positive Rate', xlim=(0, 1), ylim=(0, 1)) for i in range(1,3): ax[i].plot([0,1],[0,1],linestyle = '--',lw = 2,color = 'black') ax[i].set(title=' ', xlabel='  ', ylabel='   ', xlim=(0, 1), ylim=(0, 1)) plt.show();

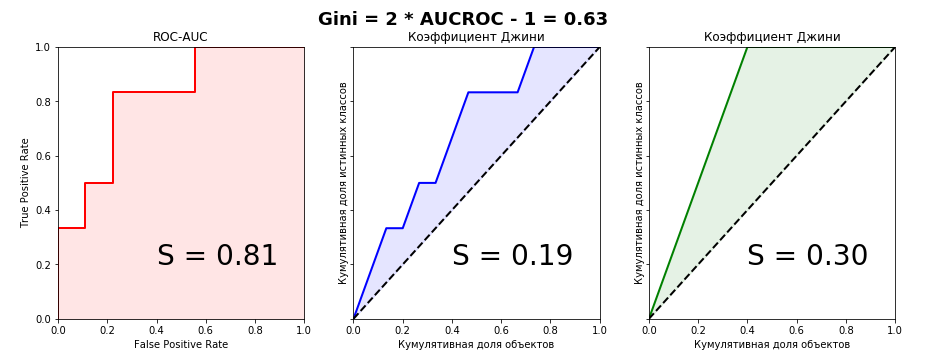
メトリックのグラフィカル表現から接続をキャッチすることは不可能であることが明確にわかるため、代数的同等性を証明します。私はこれを2つの方法で行うことができました-パラメトリック（積分による）とノンパラメトリック（Wilcoxon-Mann-Whitney統計による）。 2番目の方法は、二重積分を含む複数階の分数がなくてもはるかに簡単なので、詳細に説明します。証拠をさらに検討するために、用語を定義します。真のクラスの累積シェアは真の陽性率に他なりません。オブジェクトの累積割合は、ランク付けされた行のオブジェクトの数です（間隔にスケーリングする場合）

$（0、1）$ -それぞれ、オブジェクトの割合）。

証明を理解するには、ROC-AUCメトリックの基本的な理解が必要です。それが一般的に何であるか、グラフがどのように構築されるか、どの軸にあるか。 Alexander Dyakonovのブログの記事「AUC ROC（error curve under area）」をお勧めします

次の表記法を紹介します。

$n$ -サンプル内のオブジェクトの数
$n_0$ -クラス「0」のオブジェクトの数
$n_1$ -クラス「1」のオブジェクトの数
$TP$ -真の正（真のクラスのモデルの正解は、所定のしきい値で「1」です）
$FP$ -偽陽性（所定のしきい値での真のクラス「0」に対するモデルの誤った応答）
$Tpr$ -真の陽性率（比率 $TP$ に $n_1$ ）
$Fpr$ -偽陽性率（比率） $FP$ に $n_0$ ）
$i、j$ -アイテムの現在のインデックス。

パラメトリック法

ROC曲線のパラメトリック方程式は、次のように記述できます。

$AUC = \ int_ {0} ^ {1} TPR \エンスペースdFPR = \ int_ {0} ^ {1} \ frac {TP} {n_1} \エンスペースd \ frac {FP} {n_0} = \ frac {1 } {n_1 * n_0} \ int_ {0} ^ {1} TP \エンスペースdFP \ hspace {35pt}（3）$

リフトカーブを軸にプロットする場合

$X$ 以前に降順でソートされたオブジェクトの割合（その数）を別にします。したがって、Gini係数のパラメトリック方程式は次のようになります。

$AUC = \ int_ {0} ^ {1} TPR \エンスペースd \ frac {TP + FP} {n_1 + n_0}-0.5 \ hspace {35pt}（4）$

両方のモデルの式（4）を式（1）に代入して変換すると、式（3）がパーツの1つに代入できることがわかります。これにより、最終的に正規化されたGini（2）の美しい式が得られます

ノンパラメトリック法

その証明において、私は確率論の基本的な仮定に頼った。 AUC ROC値は、ウィルコクソン-マン-ホイットニーの統計値と等しいことが知られています。

$AUCROC = \ frac {\ sum_ {i = 1} ^ {n_1} \ sum_ {j = 1} ^ {n_0} S（x_i、x_j）} {n_1 * n_0} \ hspace {15pt}（5）$

$S（x_i、x_j）= \ begin {cases} 1、\ enspace x_i> x_j \\ \ frac {1} {2}、\ enspace x_i = x_j \\ 0、\ enspace x_i <x_j \ end {cases}$

どこで

$x_i$ -分布 "1"からのi番目のオブジェクトに対するアルゴリズムの応答、

$x_j$ -分布 "0"からのj番目のオブジェクトに対するアルゴリズムの応答

この式の証明は、たとえばここにあります。

これは非常に直感的に解釈されます。最初のオブジェクトが分布「1」から、2番目が分布「0」からランダムにオブジェクトのペアを抽出した場合、最初のオブジェクトが2番目の予測値以上の予測値を持つ確率オブジェクトはAUC ROCの値と等しい。組み合わせでは、このようなオブジェクトのペアの数は次のように簡単に計算できます。

$n_1 * n_0$ 。

モデルに予測させる

$k$ セットからの可能な値

$S = \ {s_1、\ドット、s_k \}$ どこで

$s_1 <\ enspace ... \ enspace <s_k$ そして

$S$ -ある種の確率分布。その要素は区間で値を取ります

$[0,1]$ 。

させる

$S_ {n_1}$ オブジェクトが取る値のセット

$n_1$ そして

$S_ {n_1} \サブセットeq S$ 。させる

$S_ {n_0}$ オブジェクトが取る値のセット

$n_0$ そして

$S_ {n_0} \サブセットeq S$ 。明らかに、セット

$S_ {n_1}$ そして

$S_ {n_0}$ 交差する可能性があります。

示す

$p_ {n_ {0}} ^ {i}$ オブジェクトの確率として

$n_0$ 問題になります

$s_i$ 、そして

$p_ {n_ {1}} ^ {i}$ オブジェクトの確率として

$n_1$ 問題になります

$s_i$ 。それから

$\ sum_ {i = 1} ^ {k} p_ {n_ {0}} ^ {i} = 1$ そして

$\ sum_ {i = 1} ^ {k} p_ {n_ {1}} ^ {i} = 1$

先験的確率を持つ

$\ pi$ 各サンプルオブジェクトに対して、オブジェクトが値を取る確率を決定する式を書くことができます

$s_i$ ：

$p_ {n} ^ {i} = \ pi p_ {n_ {0}} ^ {i} +（1- \ pi）p_ {n_ {1}} ^ {i}$

3つの分布関数を定義します。

-クラス「1」のオブジェクトの場合

-クラス「0」のオブジェクトの場合

-サンプルのすべてのオブジェクト

$CDF_ {n_ {1}} ^ {i} = \ sum_ {j = 1} ^ {i} p_ {n_ {1}} ^ {i} \ hspace {10pt} i = 1、\ドット、k$

$CDF_ {n_ {0}} ^ {i} = \ sum_ {j = 1} ^ {i} p_ {n_ {0}} ^ {i} \ hspace {10pt} i = 1、\ドット、k$

$CDF_ {n} ^ {i} = \ sum_ {j = 1} ^ {i} p_ {n} ^ {i} \ hspace {10pt} i = 1、\ドット、k$

クレジットスコアリング問題の2つのクラスの分布関数の例は次のようになります。

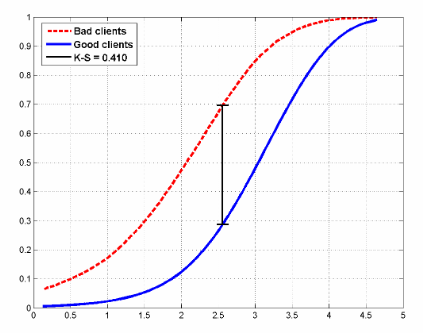
この図は、モデルの評価にも使用されるコルモゴロフ-スミルノフ統計も示しています。

確率的な形でウィルコクソンの式を書き、それを変換します。

$AUCROC = P（S_ {n_1}> S_ {n_1}）+ \ frac {1} {2} P（S_ {n_1} = S_ {n_1}）= \\ \ sum_ {i = 1} ^ {k} P（S_ {n_1} \ geq s_ {i-1}）P（S_ {n_0} = s_ {i}）+ \ frac {1} {2} \ sum_ {i = 1} ^ {k} P（S_ {n_1} = s_ {i}）P（S_ {n_0} = s_ {i}）= \\ \ sum_ {i = 1} ^ {k} \ big（（P（S_ {n_1} \ geq s_ {i -1}）+ \ frac {1} {2} P（S_ {n_1} = s_ {i}）\ big）P（S_ {n_0} = s_ {i}）= \\ \ sum_ {i = 1} ^ {k} \ frac {1} {2} \ big（（P（S_ {n_1} \ geq s_ {i}）+（P（S_ {n_1} \ geq s_ {i-1}）\ big）P （S_ {n_0} = s_ {i}）= \\ \ sum_ {i = 1} ^ {k} \ frac {1} {2}（CDF_ {n_ {1}} ^ {i} + CDF_ {n_ { 1}} ^ {i-1}）（CDF_ {n_ {0}} ^ {i}-CDF_ {n_ {0}} ^ {i-1}）\ hspace {15pt}（6）$

リフト曲線の下の領域に対して同様の式を書くことができます（2つの領域の合計で構成され、そのうちの1つは常に0.5であることに注意してください）。

$AUC Lift = Gini_ {model} + 0.5 = \ sum_ {i = 1} ^ {k} \ frac {1} {2}（CDF_ {n_ {1}} ^ {i} + CDF_ {n_ {1}} ^ {i-1}）（CDF_ {n} ^ {i}-CDF_ {n} ^ {i-1}）\ hspace {15pt}（7）$

そして今、それを変換します：

$AUCリフト= Gini + 0.5 = \ sum_ {i = 1} ^ {k} \ frac {1} {2}（CDF_ {n_ {1}} ^ {i} + CDF_ {n_ {1}} ^ {i -1}）（CDF_ {n} ^ {i}-CDF_ {n} ^ {i-1}）= \\ \ sum_ {i = 1} ^ {k} \ frac {1} {2}（CDF_ { n_ {1}} ^ {i} + CDF_ {n_ {1}} ^ {i-1}）\ big（\ pi（CDF_ {n_ {1}} ^ {i}-CDF_ {n_ {1}} ^ {i-1}）+（1- \ pi）（CDF_ {n_ {0}} ^ {i}-CDF_ {n_ {0}} ^ {i-1}）\ big）= \\（1- \ pi）\ sum_ {i = 1} ^ {k} \ frac {1} {2}（CDF_ {n_ {1}} ^ {i} + CDF_ {n_ {1}} ^ {i-1}）（CDF_ {n_ {0}} ^ {i}-CDF_ {n_ {0}} ^ {i-1}）+ \\ + \ pi \ sum_ {i = 1} ^ {k} \ frac {1} {2} （CDF_ {n_ {1}} ^ {i} + CDF_ {n_ {1}} ^ {i-1}）（CDF_ {n_ {1}} ^ {i}-CDF_ {n_ {1}} ^ {i -1}）= \\（1- \ pi）AUCROC + \ frac {1} {2} \ pi \ sum_ {i = 1} ^ {k} \ big（（CDF_ {n_ {1}} ^ {i }）_ {} ^ {2}-（CDF_ {n_ {0}} ^ {i-1}）_ {} ^ {2} \ big）= \\（1- \ pi）AUCROC + \ frac {1 } {2} \ pi \ hspace {15pt}（8）$

理想的なモデルの場合、式は単純に記述されます。

$Gini_ {perfect} = \ frac {1} {2}（1- \ pi）\ hspace {15pt}（9）$

したがって、（8）および（9）から、以下を取得します。

$Gini_ {normalized} = \ frac {Gini_ {model}} {Gini_ {perfect}} = \ frac {（1- \ pi）AUCROC + \ frac {1} {2}} {\ frac {1} {2} （1- \ pi）} = 2AUCROC-1$

彼らが学校で言ったように、それは証明する必要がありました。

3.実用化

記事の冒頭で述べたように、Gini係数は、銀行融資、保険、ターゲットマーケティングなど、多くの分野でモデルを評価するために使用されます。これには非常に合理的な説明があります。この記事では、特定の分野での統計の実用化について詳しく説明するつもりはありません。このトピックについては多くの本が書かれていますが、このトピックについては簡単に説明します。

クレジットスコアリング

世界中の銀行は、毎日数千件の融資申し込みを受け取っています。もちろん、クライアントが単にローンを返済しないリスクを何らかの方法で評価する必要があるため、クライアントが属性空間によってローンを返済しない確率を評価する予測モデルが開発され、これらのモデルは最初に評価され、モデルが成功した場合、確率の最適なしきい値（しきい値）を選択します。最適なしきい値の選択は、銀行の方針によって決まります。しきい値を選択する際の分析のタスクは、ローン発行の拒否に関連する利益損失のリスクを最小限に抑えることです。ただし、しきい値を選択するには、品質モデルが必要です。銀行セクターの主な品質指標：

ジニ係数
コルモゴロフ-スミルノフ統計（「悪い」借り手と「良い」借り手の累積分布関数の最大差として計算。上の図は、分布とこれらの統計を示しています）
発散係数（これは、「悪い」借り手と「良い」借り手のスコアリングポイントの分布の数学的期待値の差の推定値です。これらの分布の分散によって正規化されます。

私はここに住んでいますが、ロシアの状況はわかりませんが、ヨーロッパでは、ジニ係数が最も広く使用されています。北米では、コルモゴロフ-スミルノフ統計です。

保険

この分野では、すべてが銀行部門に似ていますが、唯一の違いは、顧客を保険請求を提出する人と提出しない人に分ける必要があることです。この領域の実際の例を考えてみましょう。リフト曲線の1つの特徴がはっきりと見えるようになります-ターゲット変数の非常に不均衡なクラスでは、曲線はROC曲線とほぼ完全に一致します。

数か月前、Kaggleはポルトセグーロのセーフドライバー予測コンペティションを開催しました。このコンテストでは、保険請求を予測するだけで、保険請求を提出しました。そして、私は自分自身の愚かさによって、間違った提出を選択することで銀を逃しました。

それは非常に奇妙であると同時に信じられないほど有益な競争でした。記録的な参加者数-5169。競争の勝者Michael JahrerはC ++ / CUDAのみでコードを記述しました。これは賞賛され尊敬されています。

ポルトセグロはブラジルの自動車保険会社です。

データセットは、列車の595,207行、テストの892,816行、および53の匿名標識で構成されていました。ターゲットのクラスの割合は3％と97％です。これは数行で行われるため、単純なベースラインを作成し、グラフを作成します。曲線はほぼ完全に一致することに注意してください。リフト曲線とROC曲線の下の領域の差は0.005です。

Pythonコード

 from sklearn.model_selection import train_test_split import xgboost as xgb from scipy.interpolate import interp1d from scipy.integrate import quad df = pd.read_csv('train.csv', index_col='id') unwanted = df.columns[df.columns.str.startswith('ps_calc_')] df.drop(unwanted,inplace=True,axis=1) df.fillna(-999, inplace=True) train, test = train_test_split(df, stratify=df.target, test_size=0.25, random_state=1) estimator = xgb.XGBClassifier(seed=1, n_jobs=-1) estimator.fit(train.drop('target', axis=1), train.target) pred = estimator.predict_proba(test.drop('target', axis=1))[:, 1] test['predict'] = pred actual = test.target.values predict = test.predict.values data = zip(actual, predict) sorted_data = sorted(data, key=lambda d: d[1], reverse=True) sorted_actual = [d[0] for d in sorted_data] cumulative_actual = np.cumsum(sorted_actual) / sum(actual) cumulative_index = np.arange(1, len(cumulative_actual)+1) / len(predict) cumulative_actual_perfect = np.cumsum(sorted(actual, reverse=True)) / sum(actual) aucroc = roc_auc_score(actual, predict) gini = 2*roc_auc_score(actual, predict)-1 fpr, tpr, t = roc_curve(actual, predict) x_values = [0] + list(cumulative_index) y_values = [0] + list(cumulative_actual) y_values_perfect = [0] + list(cumulative_actual_perfect) fig, ax = plt.subplots(nrows=1,ncols=3, sharey=True, figsize=(18, 6)) fig.suptitle('Gini = {:0.3f}\n\n'.format(gini),fontsize = 26, fontweight='bold') ax[0].plot([0]+fpr.tolist(), [0]+tpr.tolist(), lw=2, color = 'red') ax[0].plot([0]+fpr.tolist(), [0]+tpr.tolist(), lw = 2, color = 'red') ax[0].fill_between([0]+fpr.tolist(), [0]+tpr.tolist(), color = 'red', alpha=0.1) ax[0].text(0.4,0.2,'S = {:0.3f}'.format(aucroc),fontsize = 28) ax[1].plot(x_values, y_values, lw = 2, color = 'blue') ax[1].fill_between(x_values, x_values, y_values, color = 'blue', alpha=0.1) ax[1].text(0.4,0.2,'S = {:0.3f}'.format(S_pred),fontsize = 28) ax[2].plot(x_values, y_values_perfect, lw = 2, color = 'green') ax[2].fill_between(x_values, x_values, y_values_perfect, color = 'green', alpha=0.1) ax[2].text(0.4,0.2,'S = {:0.3f}'.format(S_actual),fontsize = 28) ax[0].set(title='ROC-AUC XGBoost Baseline', xlabel='False Positive Rate', ylabel='True Positive Rate', xlim=(0, 1), ylim=(0, 1)) ax[1].set(title='Gini XGBoost Baseline') ax[2].set(title='Gini Perfect') for i in range(1,3): ax[i].plot([0,1],[0,1],linestyle = '--',lw = 2,color = 'black') ax[i].set(xlabel='Share of clients', ylabel='True Positive Rate', xlim=(0, 1), ylim=(0, 1)) plt.show();

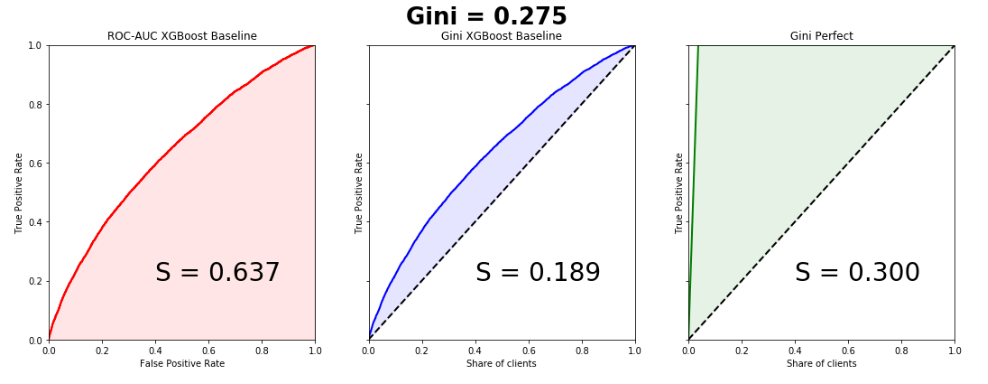
勝者のモデルのジニ係数は0.29698です。

私にとって、ミステリーは、主催者がまだ兆候を認識し、信じられないほどのデータ前処理を行うことで達成したかったものです。これが、勝者を含むすべてのモデルが本質的にゴミであることが判明した理由の1つです。おそらくただのPRであり、ブラジル人を除いて世界中の誰もがポルト・セグーロを知らなかったが、今では多くの人が知っている。

ターゲットマーケティング

この領域では、Gini係数とリフト曲線の真の意味を最もよく理解できます。何らかの理由で、ほとんどすべての書籍や記事に、電子メールマーケティングキャンペーンの例が挙げられていますが、これは時代錯誤と思われます。free2playゲームの領域から人工的なビジネスタスクを作成しましょう。私たちはかつて私たちのゲームをプレイし、何らかの理由で落ちたユーザーのデータベースを持っています。ゲームプロジェクトにそれらを返したいと思います。各ユーザーに対して、モデルの構築に基づいて、特定の属性スペース（プロジェクトの時間、費やしたレベル、到達したレベルなど）があります。 Gini係数によってモデルを評価し、リフト曲線を作成します。

マーケティングキャンペーンの枠組みで、何らかの方法でユーザー（メール、ソーシャルネットワーク）との連絡を確立するとします。1人のユーザーとの連絡の価格は2ルーブルです。Lifetime Valueが5ルーブルであることを知っています。マーケティングキャンペーンの効果を最適化する必要があります。サンプルに100人のユーザーがいて、そのうち30人が戻ってくるとします。したがって、100％のユーザーとの連絡を確立すると、マーケティングキャンペーンに200ルーブルを費やし、150ルーブルの収入を得ます。これはキャンペーンの失敗です。リフト曲線チャートを検討してください。 50％のユーザーと連絡を取り、90％のユーザーが戻ってくることを確認しています。キャンペーン費用-100ルーブル、収入135。私たちは黒人です。したがって、Lift Curveを使用すると、マーケティング会社を最適な方法で最適化できます。

4.バブルソート

Gini係数には、かなり面白いが非常に有用な解釈があり、これを使用して簡単に計算することもできます。数値的には次と等しいことがわかります：

$Gini_{normalized} = \frac{Swaps_{random} - Swaps_{sorted}}{Swaps_{random}}$

どこで

$Swaps_{sorted}$ ターゲット変数の真のリストを取得するためにランク付けされたリストで実行する必要がある順列の数、

$Swaps_{random}$ -ランダムアルゴリズムの予測の順列の数。バブルを使用して基本的なソートを記述し、表示します。

$[1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]\\ [1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0]$

Pythonコード

 actual = [1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0] predict = [0.9, 0.3, 0.8, 0.75, 0.65, 0.6, 0.78, 0.7, 0.05, 0.4, 0.4, 0.05, 0.5, 0.1, 0.1] data = zip(actual, predict) sorted_data = sorted(data, key=lambda d: d[1], reverse=False) sorted_actual = [d[0] for d in sorted_data] swaps=0 n = len(sorted_actual) array = sorted_actual for i in range(1,n): flag = 0 for j in range(ni): if array[j]>array[j+1]: array[j], array[j+1] = array[j+1], array[j] flag = 1 swaps+=1 if flag == 0: break print(" : ", swaps)

順列の数：10

組み合わせでは、ランダムアルゴリズムの順列の数を簡単に計算できます。

$Swaps_{random} = \frac{6*9}{2} = 27$

このように：

$Gini_{normalized} = \frac{27 - 10}{27} = 0.63$

上記のおもちゃの例のように、係数の値を取得したことがわかります。

この記事が参考になり、この品質指標に関するいくつかの神話を払拭したことを願っています。

ジニ係数。 経済学から機械学習まで

経済学

機械学習

1.一般的な理解

2.代数表現。 AUC ROCとの線形関係の証明

パラメトリック法

ノンパラメトリック法

3.実用化

クレジットスコアリング

保険

ターゲットマーケティング

4.バブルソート

More articles:

ジニ係数。経済学から機械学習まで