Clever Geek Handbook

地球のリモートセンシング用のマイクロサテライト





現在、大きな宇宙船の適切な代替品である小さな宇宙船の作成と使用に大きな関心が寄せられています。



これは、マイクロサテライト（MS）の多くの利点によるものです[1]：





マイクロサテライトは、10〜100 kgの質量を持つ宇宙船です。 科学および技術の現代レベルの開発により、このクラスの衛星には、大型宇宙船に固有のほぼすべての搭載システムを搭載することが可能です：方向（パッシブおよびアクティブ）、電源、位置決定、無線通信、および搭載コンピューター複合体。



Fast Companyによると、フィンランドとアメリカの2社は、低コストのマイクロサテライトの星座全体を打ち上げる準備を進めており、これにより追跡機能が大幅に向上します。 低コストは、より多くの顧客層への使用を可能にし、多くの専門家に懸念を抱かせます[2]。



問題の声明



地球のリモートセンシングのためにマイクロサテライトの軌道を修正するために推進システムを使用する可能性の分析。



マイクロサテライト推進システムの供給条件。



ほとんどの宇宙作業に適したマイクロサテライトの質量特性は、20〜70 kg（Lapan TUBSat）の範囲です。



マイクロサテライトのこの質量範囲では、サイズが容易に一貫しており、衛星質量の7〜25％を占める推進システムを使用できます。



この場合、推進システムには、最大3.3 dm3の容量のタンクを備えた独自の電源システム、制御コントローラー、燃料貯蔵および供給サブシステムが必要です。



軌道の高さの増分の衛星の質量への依存



この問題を解決するために、Tsiolkovsky方程式と特性速度の計算式[3]を使用します。







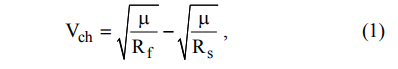
どこで 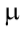-引力中心の重力パラメータ（地球用 ）; Rsは初期軌道の半径、Rs = 6945 km; Rfは最終軌道の半径kmです。



変換の結果、これらの方程式から次の式を取得できます。







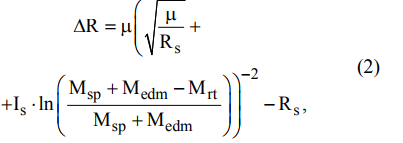
どこで 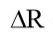-軌道の高さの増分、km; Isはエンジンの特定のインパルスです。Is= 12.750 km / s; Mspは衛星の質量kgです。 Medm-推進システムの質量、Medm = 5.33 kg; Mrtは作動流体の質量、Mrt = 0.73 kg。



プロットしましょう： 
import numpy as np import matplotlib.pyplot as plt mz=3.986*10**5 #      3/2 Rs=6945 #-     . Is=12.750#   / Medm=5.33 #     . Mrt=0.73 #     . # x -    . def dR(x): return mz*(((mz/Rs)**0.5+Is*np.log((x+Medm-Mrt)/(x+Medm)))**-2)-Rs p=np.arange(20,50,1) y=[dR(x) for x in p] plt.title('     \n    ') plt.ylabel('    .') plt.xlabel('   .') plt.plot(p,y, color='r',linewidth=2) plt.grid(True) plt.show()








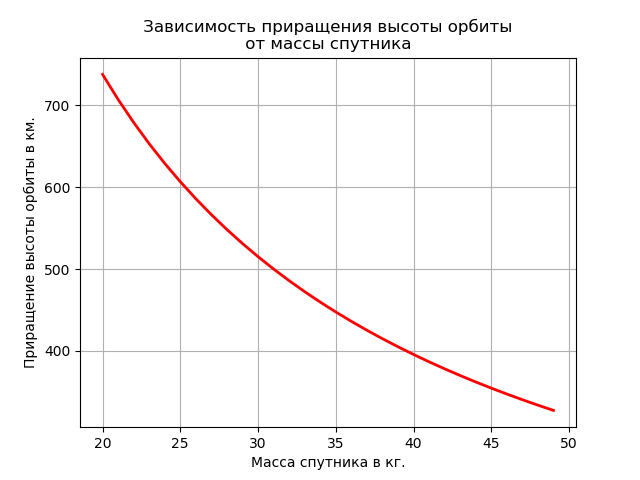
式（2）を使用して、軌道の高さの最大増分を計算できます。これにより、合計時間[3]の推進システムを提供できます。







ここで、Fはエンジンの推力、F = 0.0045 Nです。



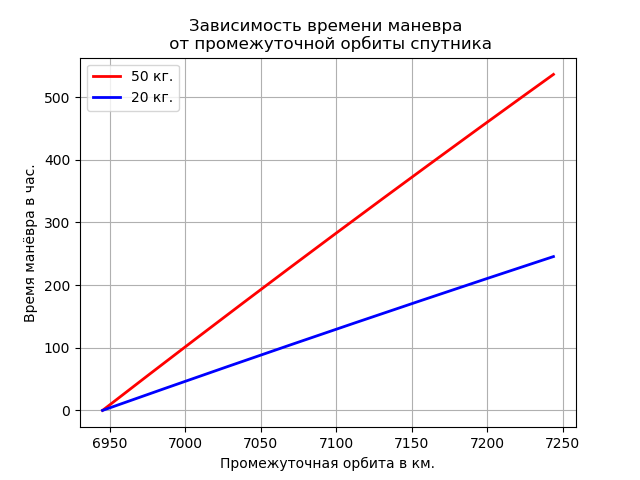
操縦時間と中間軌道



RsからRs +の範囲の衛星を任意の中間軌道（Rp）に持ち上げるのに必要な操縦時間を決定しましょう。 。



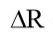操縦時間を計算するには、次の式[3]を使用できます。







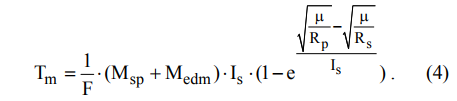
プロットしましょう： 
 import numpy as np import matplotlib.pyplot as plt mz=3.986*10**5 #      3/2 Rs=6945 #-     . Is=12.750#   / Medm=5.33 #     . Mrt=0.73 #     . F =0.0045 #   # xm -    . # Rp -    . def dR(xm,Rp): m=(np.sqrt(mz/Rp)-np.sqrt(mz/Rs))/Is return(1/(F*3600))*(xm+Medm)*Is*1000*(1-np.e**m) p=np.arange(6945,7245,1) y1=[dR(50,Rp) for Rp in p] y2=[dR(20,Rp) for Rp in p] plt.title('   \n    ') plt.ylabel('   .') plt.xlabel('   .') plt.plot(p,y1, color='r',linewidth=2, label='50 .') plt.plot(p,y2, color='b',linewidth=2, label='20 .') plt.legend(loc='best') plt.grid(True) plt.show()








軌道の平面を変更する推進システムの機能。



小型推力エンジンの影響下での軌道の傾きの変化を計算するには、次の式を使用できます[4]。







ここで、Vは軌道速度、m / sです。 iは軌道の傾きです。 uは衛星の緯度の引数です。 この式を整数形式で記述します。







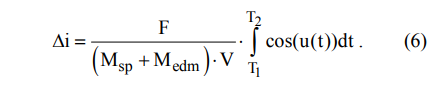
この式から、軌道の傾きを増加または減少させるには、エンジンの推力が 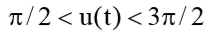一方向に行動し、いつ そして 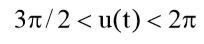方向を反対に変更します。



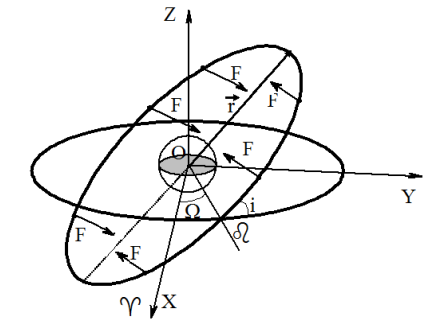
推力は、軌道面に垂直でなければなりません。 この図は、さまざまなポイントでのエンジン推力の必要な方向を示しており、直接移動する軌道の傾きが大きくなっています。







結論



地球のリモートセンシングのマイクロサテライトの軌道を修正するために推進システムを使用する可能性の分析が実行されます。





More articles:


All Articles