はじめに

あらゆる知識分野での数学的モデリングの究極の目標は、研究対象の量的特性を取得することです。 前回モデル化した銃のいくつかのパラメーターは、問題の条件に設定されました：発射体の初期速度、口径、およびそれが作られた材料。 銃身の傾斜角は、さまざまなパラメーターに起因する可能性があります。深刻な銃は、垂直面を含む干渉を許します。







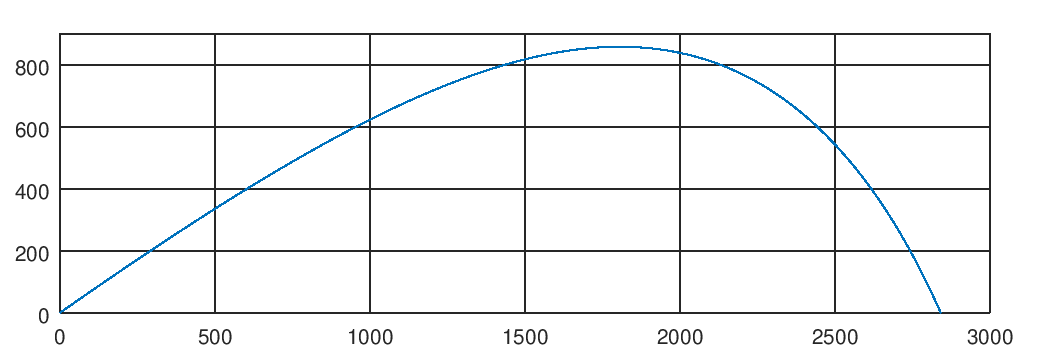
出口で、発射体の飛行経路を取得しました。これにより、銃の特性に関する示唆的なアイデアが得られます：与えられたパラメーターで、射程は2.5 kmを超え、発射体のリフトの高さは800 mを超えました。 グリッド上の鉛筆でチャート上の必要なポイントの座標を決定する場合、より正確に言うことはできません。 しかし、これはご存じのとおり、私たちの方法ではありません。 このデータを、私たちが使用しているツールによって提供される精度で、手作業なしで取得できたらいいと思います。 それが今日お話しすることです。

1.問題の声明

そのため、前回構築した数学的モデルにより、いつでも発射体の座標と速度を決定できます。 実際、次の軌跡パラメーターを計算できる関数がありました。

$$

$$\ begin {align}＆x = x（t）\\＆y = y（t）\\＆v_x = v_x（t）\\＆v_y = v_y（t）\ end {align}$$

時間の関数として。 発射物の高さはy（t）です。 どの時点で高さがゼロに等しくなるかを判断する場合、つまり方程式を解きます

$$

$$y（t）= 0$$

時間を基準にして、ある時点を見つけます $$$t ^ {*}$ そこにシェルが地面に落ちました。 座標 $$$x（t ^ {*}）$ 発射物の範囲があります。



発射物の最大高さを見つける方法は？ 弾道グラフから、発射体が上昇するにつれてその弾道はますます穏やかになり、極値では瞬間の速度が水平になり、さらに発射体が下に移動することがわかります。







数学の言語では、関数の極値を見つける必要があります $$$y = y（t）$ 。 そして、これのために何をする必要がありますか？ その導関数をゼロに等しくします！ この場合、時間微分、つまり方程式を解きます

$$

$$\ドットy（t）= 0$$

または

$$

$$v_y（t）= 0$$

なぜなら、時間の垂直座標の導関数は速度の垂直投影だからです。 この方程式の根、 $$$t ^ {**}$ 発射物が最大の高さに達する時点があります。 したがって、私たちへの関心の高さ

$$

$$h _ {\ max} = y（t ^ {**}）$$

ただ？ 以上。

2.等式ではない

そして、あなたが知っているように、ここで子猫のガバは困っています。 そもそも、方程式が（分析的に）式の形式で与えられたとしても、その解を見つけることが常に可能とは限りません。 ここに例があります

$$

$$x + 2 = e ^ {x}$$

どうですか？ シンプルですが、学校で教えられたすべてを使ってXを見つけてください。 それは同じです...





そのような方程式の解は、特にそのグラフィカルな解が明らかであるため、数値的に求める必要があります





銃のモデルの場合、すべてがやや陰湿です-私たちの方程式は式によってさえ与えられません。 大まかに言えば、ショットの非常に特定のパラメーターに対して取得された位相座標の値の表によって与えられます。 方程式はありません！



さて、この方程式を構築することに誰も気にしません。 しかし、スクリプトを書き始める前に、読者を誤解させてしまったことを謝罪したいと思います。 複数の関数を1つのOctaveスクリプトファイルに配置でき、ファイル名は関数名と必ず一致する必要があります。 スクリプトが関数の定義で始まっていなければ十分です。



ballistics.m、fm、f_air.mファイルと同じディレクトリに新しいスクリプトを作成します。 たとえば、cannon.mという名前を付けましょう。 まず、発射物のパラメーター、初期速度とショットの方向を尋ねましょう

%------------------------------------------------------------------------------- %   %------------------------------------------------------------------------------- %    global gamma = 7800; %    ( ) global c_f = 0.47; %  global d = 0.1; %------------------------------------------------------------------------------- %   %------------------------------------------------------------------------------- %   global v0 = 400; %     ( !) global alpha = 35;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、任意の時点の位相座標の値を計算する関数を作成します

 %------------------------------------------------------------------------------- %         %------------------------------------------------------------------------------- function Y = MotionOdeSolve(v0, alpha, t) %   x0 = 0; y0 = 0; vx0 = v0 * cos(deg2rad(alpha)); vy0 = v0 * sin(deg2rad(alpha)); Y0 = [x0; y0; vx0; vy0]; %    solv = lsode("f_air", Y0, [0; t]); %        t Y = [solv(2,1); solv(2,2); solv(2,3); solv(2,4)]; endfunction
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、方程式の解関数に転送される時点として2つの値のみを取得することに注意してください。初期時点（t = 0）と関心のある時点です。 したがって、solv変数には2つの位相座標ベクトルが含まれます。最初のベクトルと必要なベクトルです。 位相軌跡の終点のすべての成分をベクトルYに収集し、その値を関数から返します。



発射体の高度の時間依存性を判断するのに費用はかかりません

 %------------------------------------------------------------------------------- %         %------------------------------------------------------------------------------- function h = height(t) global v0; global alpha; Y = MotionOdeSolve(v0, alpha, t); h = Y(2); endfunction
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

受信した機能をテストする

 t1 = 10; t2 = 20; printf("h(%f) = %f, h(%f) = %f\n", t1, height(t1), t2, height(t2));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

実行するスクリプトを実行すると、コマンドウィンドウに次の出力が表示されます。

 >> cannon h(10.000000) = 855.013452, h(20.000000) = 500.106649
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

すばらしい、機能は機能します！ 同様に、水平範囲計算関数を定義します

 %------------------------------------------------------------------------------- %         t %------------------------------------------------------------------------------- function d = dist(t) global v0; global alpha; Y = MotionOdeSolve(v0, alpha, t); d = Y(1); endfunction
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

高度と範囲を計算するために、最初から興味のある時点までの運動方程式を統合するたびに見ることができます。 したがって、特定の式で表されない依存関係が得られました。 これはかなりクールです。

3.非線形方程式の数値解の原理

非線形および超越方程式を解くための数値的手法は、次の形式の方程式を解くために研ぎ澄まされています

$$

$$f（x）= 0$$

任意の方程式をこの形式にまとめるのは簡単です。 例えば

$$

$$x + 2 = e ^ {x}$$

になります

$$

$$x + 2-e ^ {x} = 0$$

どこで $$$f（x）= x + 2-e ^ {x}$ 。 この等価方程式の根は、元の根と等しくなります。 関数f（x）をプロットすると、このような画像が表示されます





方程式の根は、グラフがx軸と交差する点での引数の値です。



そのような方程式の数値解法のすべての方法には、2つの段階が含まれます。

1. ルートの初期近似を検索します
2. 与えられたエラーによるルートの改良

最初の近似では、引数f（x）の値を意味します。これは、ルートに可能な限り近いか、妥当な反復回数でメソッドの収束を保証するのに十分近い値です。



最も単純な方法は、単純反復法です。 この方法を適用するために、方程式は

$$

$$x = \ varphi（x）$$

繰り返し式に従って計算を実行します

$$

$$x_ {i + 1} = \ varphi（x_i）$$

この例では

$$

$$x_ {i + 1} = e ^ {x_i}-2$$

チャートを見てみましょう。 方程式には2つのルートがあります。 初期近似として選択して、左端のルートを見つけます $$$x_0 = -2$

$$

$$\ begin {align}＆x_1 = e ^ {x_0}-2 = e ^ {-2}-2 = -1.8647 \\＆x_2 = e ^ {x_1}-2 = e ^ {-1.8647}-2 = -1.8451 \\＆x_3 = e ^ {x_2}-2 = e ^ {-1.8451}-2 = -1.8412 \\＆x_4 = e ^ {x_3}-2 = e ^ {-1.8412}-2 = -1.8415 \\＆x_5 = e ^ {x_4}-2 = e ^ {-1.8415}-2 = -1.8414 \\＆x_6 = e ^ {x_5}-2 = e ^ {-1.8414}-2 = -1.8414 \ end {align}$$

ええ、6回目の反復から、結果の数値の4番目の符号が変化しないことは明らかです。 そのため、6回目の反復で10 ^-4未満の誤差を持つ方程式の根が見つかりました。



すべてはうまくいきますが、単純な反復の方法は常に収束するとは限りません。 任意に近い初期近似を自問自答して、この方程式の2番目のルートを見つけてみてください-何も起こりません。新しい値はそれぞれ、ルートからさらに遠くに行きます。 メソッドの収束は達成できますが、メソッドがありますが、実際にはこれは私たちの生活を著しく複雑にします。 したがって、2番目のルートを見つけるには、別の方法を使用します。 初期近似の近くで、研究中の関数をテイラー級数で展開します

$$

$$f（x）= f（x_0）+ f '（x_0）\、（x-x_0）+ \ frac {1} {2} \、f' '（x_0）\、（x-x_0）^ 2 + ...$$

関数f（x）自体を、ポイントx ₀でのグラフの接線に置き換えて、1次の小ささの項に限定します_。

$$

$$f（x）\およそf（x_0）+ f '（x_0）\、（x-x_0）$$

そして、結果の式をゼロに等しくすると、xに関してそれを解きます

$$

$$x_1 = x_0-\ frac {f（x_0）} {f '（x_0）}$$

反復式を取得します

$$

$$x_ {i + 1} = x_i-\ frac {f（x_i）} {f '（x_i）}$$

この例では

$$

$$\ begin {align}＆f（x）= x + 2-e ^ {x} \\＆f '（x）= 1-e ^ {x} \ end {align}$$

反復式

$$

$$x_ {i + 1} = x_ {i}-\ frac {x_i + 2-e ^ {x_i}} {1-e ^ {x_i}}$$

最初の近似として、 $$$x_0 = 1.0$ 反復しようとしています

$$

$$\ begin {align}＆x_1 = x_0-\ frac {x_0 + 2-e ^ {x_0}} {1-e ^ {x_0}} = 1-\ frac {1 + 2-e} {1-e} = 1.1640 \\＆x_2 = x_1-\ frac {x_1 + 2-e ^ {x_1}} {1-e ^ {x_1}} = 1.1640-\ frac {1.1640 + 2-e ^ {1.1640}} {1-e ^ {1.1640}} = 1.1464 \\＆x_3 = x_2-\ frac {x_2 + 2-e ^ {x_2}} {1-e ^ {x_2}} = 1.1464-\ frac {1.1464 + 2-e ^ {1.1464}} {1-e ^ {1.1464}} = 1.1462 \\＆x_4 = x_3-\ frac {x_3 + 2-e ^ {x_3}} {1-e ^ {x_3}} = 1.1462-\ frac {1.1462 + 2-e ^ {1.1462}} {1-e ^ {1.1462}} = 1.1462 \ end {align}$$

ご覧のとおり、この方法は4文字の精度で4回の反復で収束しました。 この方法は、ニュートン法と呼ばれます。 その利点は、迅速な収束です。 欠点の中には、初期近似の精度に対する感度が高いことと、方程式の左辺の導関数を計算する必要があることです。 方程式の分析式がない場合、数値微分の厄介な操作に頼らなければなりませんが、これは常に便利で可能とは限りません。



これらの例を挙げて、一般的な原理を説明しました。 これらの2つの方法に加えて、さらに多くの方法があります。例えば：

• 二分法 -収束が保証されることを特徴とするが、速度はかなり遅い
• コード法 -微分関数の計算を必要とせず、良好な収束率

これらすべての方法は、ルートの初期近似または分離間隔-引数f（x）の変化の間隔、関数が符号を変更する境界の探索という形で、予備的な準備が必要です。 この場合、（関数が連続的であれば）自信を持って言うことができます。分離間隔内に少なくとも1つのルートがあります。

4.砲弾の軌道のパラメーターを決定します

そのため、シェルが地面に落ちた時点を見つけます。 まず、ルート分離間隔を定義します

 % %      .    % height(t) = 0 %  . % %     t0 = 0; deltaT = 1.0; t = t0; while (height(t) >= 0) t = t + deltaT; endwhile b = t; a = t - deltaT; %    t1 = t - deltaT / 2;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これはタスクの物理的な意味に基づいて行われます。ショット後すぐに、発射物の高度は負ではありません。 高さが負になるまで、ゼロから始めてすべての瞬間をソートします。 各ステップで運動の微分方程式を再統合するため、手順が長すぎないように、十分に大きなステップ（1秒）で整理します。これは計算コストの観点から非常に高価です。 高さが負になるとすぐに、検索を終了します。 方程式h（t）= 0の根は、区間[a、b]内のどこかにあります。 この区間の中間で初期近似を取ります

$$

$$t_1 = \ frac {a + b} {2} = t-\ frac {\ Delta t} {2}$$

次に、オクターブ非線形方程式を解くための手順を実行する方程式を示します。

 %   t_end = fsolve("height", t1);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

入力関数fsolve（）は、方程式f（x）= 0の左側と初期近似値を記述する関数を取ります。 指定された精度で計算されたルート値を返します。 何の精度で？ この質問をしてデフォルト設定を使用するまで、この段階で私たちに適しています。



落下の瞬間の値を受け取ったら、発射位置からの距離を計算します

 %    d_max = dist(t_end); %     printf("Shot distance: %f, m\n", d_max);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

同様に、速度の垂直投影がゼロになる時点を見つけ、この瞬間の発射体の高さを計算します

 %------------------------------------------------------------------------------- %      %------------------------------------------------------------------------------- function v = vy(t) global v0; global alpha; Y = MotionOdeSolve(v0, alpha, t); v = Y(4); endfunction % %       .   %  % % vy(t) = 0 % %     t = t0; while (vy(t) >= 0) t = t + deltaT; endwhile %    t1 = t - deltaT / 2; %   t_hmax = fsolve("vy", t1); %      h_max = height(t_hmax); printf("Maximal height: %f, m\n", h_max);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

コマンドウィンドウで、プログラムの結果を確認できます。

 >> cannon h(10.000000) = 855.013452, h(20.000000) = 500.106649 Shot distance: 2840.991508, m Maximal height: 857.963929, m
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

また、方程式がどの程度正確に解かれたかを確認します

 >> height(t_end) ans = -1.2328e-06 >> vy(t_hmax) ans = 4.5117e-09
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

トレーニング目的では、精度は許容範囲です。

おわりに

今日は、例の単純さにもかかわらず、かなり幅広いタスクを調べました。 これで、プロセスを説明する分析的な依存関係がないことが、その特性の研究に対する障害にならないことがわかりました。 未解決の課題は、この銃で使用可能な最大射程範囲を決定することでしたが、これについては別の時間です。 ご清聴ありがとうございました！