エレキギターの周波数特性の測定と形成

芸術について話しましょう。 たとえば、音楽について。 たとえば、ギターについて。



エレキギターの作成はかなり保守的なものです。 ギター（ JTV89 ）からリアルタイムでサウンドを得ることができる信号処理での大成功にもかかわらず、ギター自体が持つべき「暖かくて真空管の」サウンドは依然として高く評価されています。 一方で、これらすべてのことから、ギターの音は、顧客が望む特性を正確に持つ必要があります。顧客は突然、ギターから特定の音を聞きたいと思ったのです。







ギターの音は、次のものによって形作られます。

1. ピックアップ位置
   
   
2. ピックアップ特性
   
   
3. 文字列型
   
   
4. 住宅と材料の共鳴特性
   
   

人が使用する弦については、もちろんギターの作成者は責任を負いません。 エレクトリックギター（半音響ではない）の音に対する身体部分の影響は、非常に宗教的なものです。 この影響は、一方では否定されませんが、他方では誰もこれを考慮する方法を本当に知りません（そして、彼が知っていると言ったとしても、彼はおそらく何も明白に説明することができないでしょう）。



ピックアップは残ります。 それらの位置と信号伝送特性。 これは、測定、比較、および考慮することができます。 これらの問題については、かなり発展した複雑な理論的根拠があります。

理論部

センサーの位置の影響を評価するための理論的基礎は、 ここにあります 。 ここでセンサーの伝達特性の簡単な理論的説明。 私の側では、あなたが英語を読まないように、このすべてをできるだけ短く語ろうとします。



ギターの弦は、両端で結ばれたロープです。 私たちが彼女をぐいと動かすと、彼女は振動し始めます。なぜなら彼女は愛着があり、どこにも逃げられないからです。 しかし、これがどのように起こるかについての重要な側面があります。 弦はさまざまな周期で振動します。 文字列の長さの倍数の期間：1、½、¼、⅛、...これは、次の図で表すことができます。

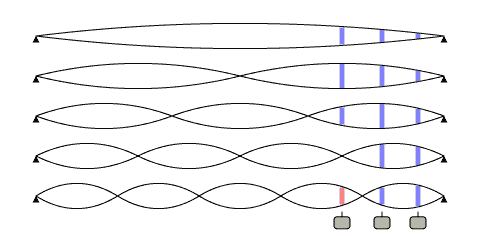
弦の高調波。 www.till.com/articles/PickupResponseからの写真

写真を注意深く見て、自分でギターを試してみることができます。 ひもを引っ張り、ひもの真ん中で指を軽く触れます。 写真からわかるように、このような動きは、少なくともこの場所にあるすべての奇数倍音を消し去り、音は消えませんが、多少変化します。 この手法は、指を真ん中に持って弦を引っ張り、ひもを引っ張ってから指で触るとひらひらと呼ばれる場合、 自然なひらひらと呼ばれます。 しかし、これは歌詞です。 私たちにとって重要なことは、多くの周波数があり、実際、すべてが弦の長さの倍数である期間に限定されないことです。



そしてここで、ピックアップが弦の領域に磁場を生成することを覚えておく必要があります。 このストリングでは、金属ストリングがセンサーの真上で振動し、何らかの方法で摂動します。 このため、ファラデーの法則に従ってセンサー回路に電流が生成されます。 そして、センサーの真上にある弦のあらゆる種類の速度は、私たちにとって興味深いものです。



物理学者は、ストリング内のある場所を移動するストリングの相対（正規化された）速度は、次の式で表されることを発見しました。

$$

$$V = sin（X / L）、\タグ{1}$$

Xはナット（下部）からピックアップまでの距離、 Lは弦の振動部分の長さです（いくつか予約がありますが、省略します）。



距離Xに注意してください。 弦が1つの基本高調波のみで発振した場合、この値の最大値は弦の中心に正確に収まります（正弦と半分は1に等しい）







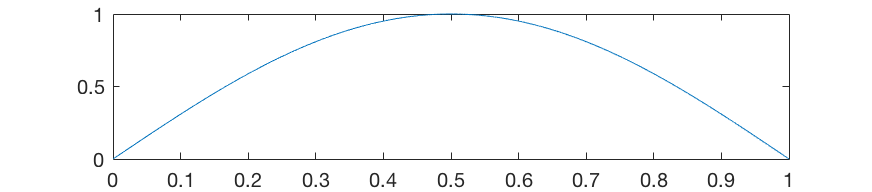
ただし、弦には他の高調波もあり、高調波の強度はそれらの数の2乗に比例して減少し、2番目は4倍、3番目は9などとなります。 2次高調波を追加しても、弦の速度が変化し、その分布が非対称になります。







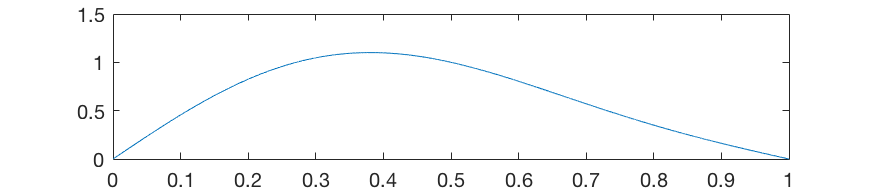
そして、「すべての」高調波を要約すると、最大値はナットから正確に⅓の位置にシフトします。







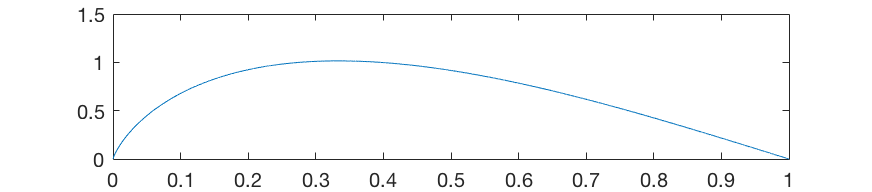
この事実により、ギター本体のセンサーと共振器の穴の位置が決まります。



トピックに戻ります。 各弦には、独自の基本周波数F ₀と、弦の主要な長さL _0があります。 明らかに、サウンディングの「長さ」が変化するときの周波数の変化は、基本周波数に反比例します（長さが長いほど、周波数は低くなります）。

$$

$$F / F_0 = L_0 / L$$

これを式1で代用できます。

$$

$$V = sin（\ pi XF / L_0F_0）、\ tag {2}$$

ここに $$$\ pi X / L_0F_0$ -定数。センサーが弦の1箇所より上にあり、速度が正弦波的に周波数に依存することが判明した場合。 当然、速度の兆候は私たちの興味を引くものではないため、上記の記事のように、この依存関係をデシベルで描くことができます。









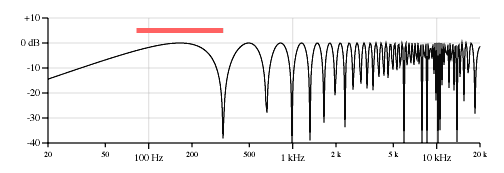
ゼロ幅センサーによる弦の「知覚」の理論的な周波数応答。 ここからの写真



対数周波数スケールでは、サイン振幅のグラフはかなり神秘的で異常に見えます...しかし、式（2）から、 Xが変化すると、この全体像が周波数軸に対して左右に移動することが明らかです。 これは、実際には、 ブリッジセンサーとネックセンサーの特徴的な音を形成します（これがどのように配置されているかを示す図があります） 。 橋の場合、最初のピークは右に、首の場合は左になります。 ブリッジXの場合、非常に小さいため、Fは最初のピークに到達するためにより大きくする必要があります。 したがって、ブリッジは低音が少なく、中音域が多いという特徴があります。



これはセンサーの位置で停止できますが、それだけではありません。



ゲージは、音が出るギターの上の点ではありません。 センサーには幅があります。 つまり センサーはそれ自体の上にあるポイントのセットに音を「収集」して追加し、それぞれの周波数応答がわずかにシフトします。 または巧妙な言葉で-積分はセンサーと文字列の交差の全長に沿って取られます（ ここでは積分を恐れない人のために ）。 この積分から、サインが1つではなく、2つあることがわかります。 両方とも周波数に依存し、1つはXに依存し、もう1つはWセンサーの幅に依存します。









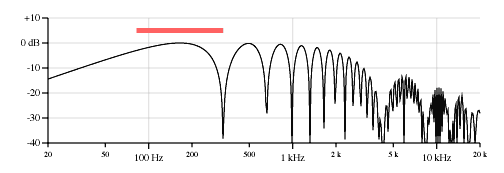
有限幅のセンサーによる弦の「知覚」の理論的周波数応答。 http://www.till.com/articles/PickupResponse/からの写真



このようなものは数学的に見えます：

$$$V = \ frac {1} {kW} sin（\ frac {k} {2} XF）sin（kWF）、\ tag {3}$

ここで、 kは文字列依存の定数です。 2による除算を考慮しても、WはXよりも小さいことがあるため、グラフには別のピークがあり、これは高周波に向かって強くシフトします。



そして、ここで最も不快な場所で周波数応答（CH）にある種の悪い穴があります。 一方、Wを展開すると、周波数応答の穴は消えますが、式（3）の分母のWであるため、信号振幅は減少します。一般に、奇妙なことに、解決される問題があります。自動的に。



センサーの場所について多くのことを話しました。 しかし、彼がどのように信号を伝えるかについてはほとんどありません。 センサーは共振を伴う2次RLC回路であり、その周波数応答は次のようになります。









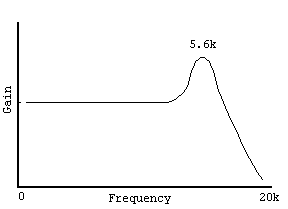
二次共振回路としての典型的なセンサーの周波数応答。 www.muzique.com/lab/pickups.htmからの写真



共鳴ピークは、センサーに幅があるという事実によって形成された穴の一部を優雅にカバーします。 そして、ギターを作成するためのすべての技術は、どの音にも音量の落ち込みがなく、適切な場所にピークがあるようにすることです。 ただし、この記事では、これについて特別なことは言いません。 これは、たとえば次のように測定できます 。



そして今、何が起こっているのかをおおまかに理解したら、実際に測定したものと得たものを説明します。

インストールおよび処理アルゴリズム

ギターから出る音と、弦を引いたときに聞こえる音がどのように異なるかを知りたいと思いました。

設置と測定に関する2つの言葉

これを判断するために、Shure M58マイクを使用しました。 その人気により、おおよその周波数応答はどこにでもあります。 したがって、「実際の音」（弦とボディによって決定されます）を測定できます。 次に、センサーの反対側に（録音に最適な距離に）マイクを配置します。 彼らはひもを引っ張った。 マイクは、最初の部分のポイント（3.4）によって決定されたものを記録し、それらすべてをセンサーに記録しました。 それから、マイクから録音された音をセンサーから録音された音から「減算」し、実際の音、ギターが作られているもの、弦が作られている弦から分離して、センサーが実際に音で行うことを確認します。 このすべてを実行し、あらゆる種類のグラフを作成する方法を知っているプログラムを作成しました。



実際、すべてはそれほど単純ではありませんが、最後にそれについてです。

どのデバイスとソフトウェア、もう一度繰り返しますか？

• サウンドカードEMU 0204
  
  
• マイクShure M58
  
  
• フェンダーストラトキャスターリッチーブラックモア版
  
  
• Music Man JP7のマスターコピー
  
  
• C＃での自動信号処理プログラム（NAudio、MathNet）
  
  
• 追加の分析：Excel、Matlab
  
  

アルゴリズム

1. 左のチャンネルではマイクを録音し、右のチャンネルではギターをオンにします（EMUで許可されています）。
   
   
2. 「同一の」信号がセンサーとマイクに記録されるように、1つのストリングをN回引きます。 音符の間に無音の間隔があることを確認します。
   
   
3. ノイズを除去し、信号を目に少し合わせます（ただし、これは必要ありません）
   
   
4. レコードから、マイクからの音、センサーからの音の2つの配列で個々の音を記録します。
   
   
5. すべての配列をレコードで正規化し、ノートが同じ「単位時間あたりのパワー」を持つようにします
   
   
6. 各配列に対して、 フーリエ変換 N = 32768を実行します（ただし、別の16384も実行できます）
   
   
7. アレイのスペクトルで、実際に音の音に対応するピークを選択し、滑らかにします（奇妙なことに、実際には評価に役立たないのは音そのものです）
   
   
8. センサーの各スペクトルからマイクの各スペクトルを減算します（マイクの独自の周波数応答がある場合）。
   
   
9. すべての周波数の結果を平均し、センサーからの音とマイクに録音された音の違いを特徴付けるスペクトルを取得します。
   
   

プロセスの一部を少し見てみましょう。

レコードから重要な部分を強調する

分離は、非常に単純な原則に従って行われます。かなり長い時間、平均してある境界値を超える信号がある場合、注意が必要です。



これを行うには、次のことを行います。

1. センサー信号の絶対値を取得します。
   
   
2. 定数Cを追加します（ゼロにならないように、対数をとる必要があるため）。
   
   
3. デシベル単位で翻訳します。
   
   
4. 移動平均で滑らか。
   
   
5. 配列全体を調べて、信号がLim定数よりも大きい部分を選択します。
   
   
6. 傾きが短すぎる。
   
   
7. センサーからの信号はマイクと同じ場所にあるため、同じ境界でマイクの信号を遮断します。
   
   
8. ノートの「スライス」を含む2つの配列を返します。
   
   

正規化

すべてのノートは異なる音量で録音され、マイクとセンサーからの音量は異なります。 したがって、比較できるようにするには、すべてを揃える必要があります。 これを行うには、次のことを行います。

1. 参照「トリム」を使用し、それについて「単位時間あたりの電力」を考慮します。
   
   

$$

$$P_i = \ frac {1} {N} \ sum | r |$$

ここで、 Nはi番目の配列のサイズ、 rはi番目の配列の値です。

1. 次に、i番目の「トリミング」ごとに、配列値を再計算します。
   
   

$$

$$r_i = r_i \ frac {P_ {ref}} {P_i}$$

高調波

各スクラップが正規化された後、そのスクラップからフーリエが取得され、そのスペクトルが計算されます。 廃棄する必要があるスペクトルには多くの余分なものがあります。 たとえば、実際には、大きくはあるが非常に可変的な振幅を持つ演奏ノートです。 これを行うには、まずこれらすべてのピークを見つけます。 どうやって？

1. スペクトル全体に対して、係数が0.05の移動平均で二重平滑化を行います。
   
   
2. 移動平均では、任意のポイントの「先史時代」が大きな役割を果たし始めるため、スムージングによりシリーズがオリジナルに遅れをとることになります。 これを回避するために、元の系列と平滑化された系列の相関をチェックすることによりオフセットが検出されます。 この相関を最大にするオフセットが選択されます。
   
   
3. その後、元の系列の標準偏差の 1.5 標準偏差だけ平滑化およびシフトされたグラフを超えるポイントの連続配列があり、それらから最大値が取得されます。 次のようになります。
   
   

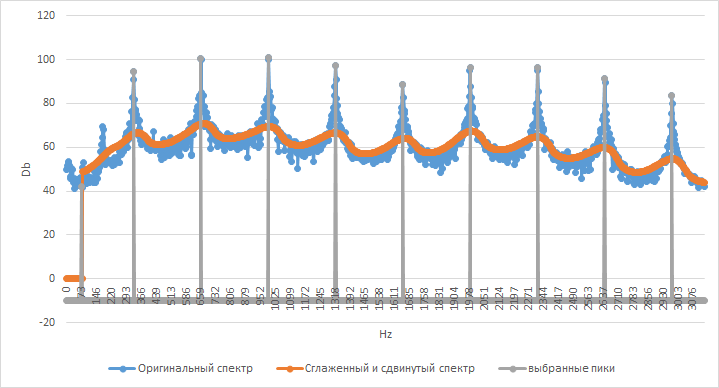
最初のオクターブのMi音のスペクトルとそれがどのように平滑化されるか



さらに、各ピークに関して、元のシリーズの±Mポイントを、平滑化されてシフトされたシリーズのポイントに置き換えます。 原則として、スムースなものをすぐに取ることができましたが、重要なものを見逃すことはありませんでした。



したがって、マイクとセンサーの両方でピークのない行を取得します。

周波数応答を取得する

取得したセンサーとマイクの行を互いに減算し、平均化すると、次のようになります。





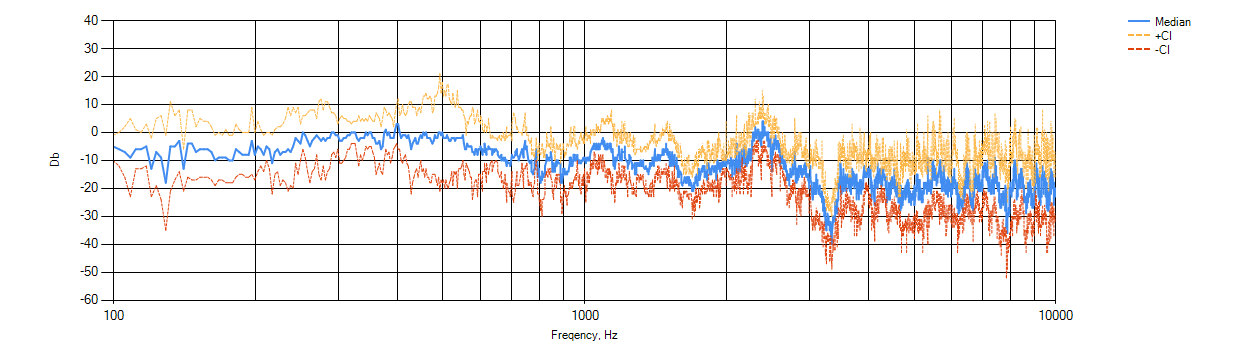
JP7のChXネックセンサーコピー（ある意味、センサーの伝達関数）。



CI +、CIは、平均化されたシリーズのプラス/最小信頼区間です。 ここでの特定のデシベル値は、相対的な場所ほど重要ではないことを理解することが重要です。 弦のボリュームが「本当に」何であるかはわかりません。 マイクを立てることができ、近くに置くことができます。 ボリュームを正規化すると、ボリュームは完全に似たものになりましたが、実際にボリュームが似ているかどうかはわかりません。 したがって、Y軸の署名は、軸に署名しないと見苦しいため、ほとんど単純です。 Y軸には秘跡的な意味はありません。 ただし、マイクとセンサーの信号が別々に描かれているとき、それらがどのように関係しているかを見るのは興味深いことがあります。





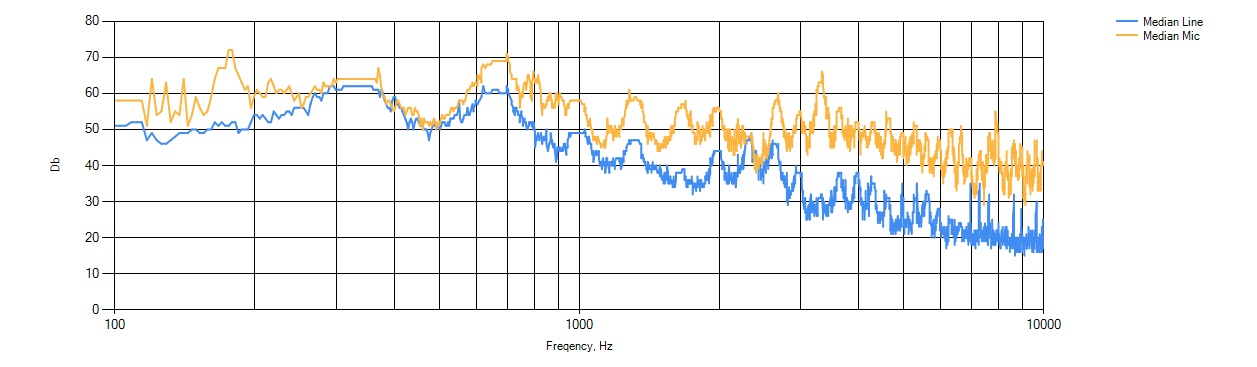
ネックセンサーコピーJP7の平滑化スペクトル。 スペクトルは平均化されて平滑化されて描画されます。



しかし、ここでも、これらのグラフは上下に安全に移動できることを覚えておく必要があります。

理論に戻る

そして、なぜ、グラフの前にこの理論全体が必要だったのですか？ これらのことはどのように関係していますか？ ここが最も興味深い部分です。



JP7の周波数応答と、650 mmのネック長、下部ナットからのセンサーの距離130 mm（ネック）、センサーの幅2インチ（51 mm）、および最初のオクターブMi 328 328 Hzについて計算された同じ理論的な応答を考えてみましょう。







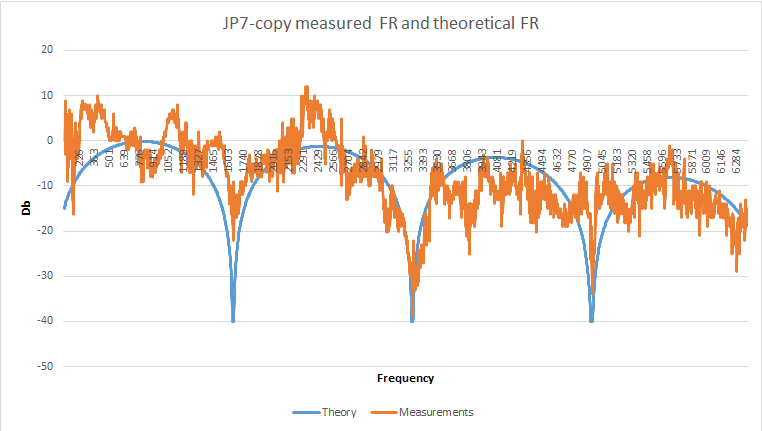
センサーの位置に関連する障害が理論上の障害とどのように一致するかが明確にわかります。 sin（pi * 129.5 * 1620 /（640 * 328））は約0であり、これはグラフのとおり正確に半周期です。 4800 Hzの領域では、センサーの電気部品の伝達関数の共振が位置する可能性が最も高いため、ディップは小さくなります。



それは必ずしもそれほど明白ではありません。



別のギターを取ります。 フェンダーストラトキャスターリッチーブラックモア版。 Seymour Duncan Quarter Pound Flat SSL-4シングルコイルStratピックアップという複雑な名前を持つ特定のプロパティとセンサーを備えたかなり特徴的なギター。 得られた周波数応答を考慮してください。 ネックの長さは655 mm、下のナットからのセンサーの距離は150 mm（ネック）、センサーの幅は2インチ（50 mm）です（実際、非常に強力なシングルがあり、 ハムバッカーのパラメーターはそれよりも優れています）。オクターブ328 Hz：







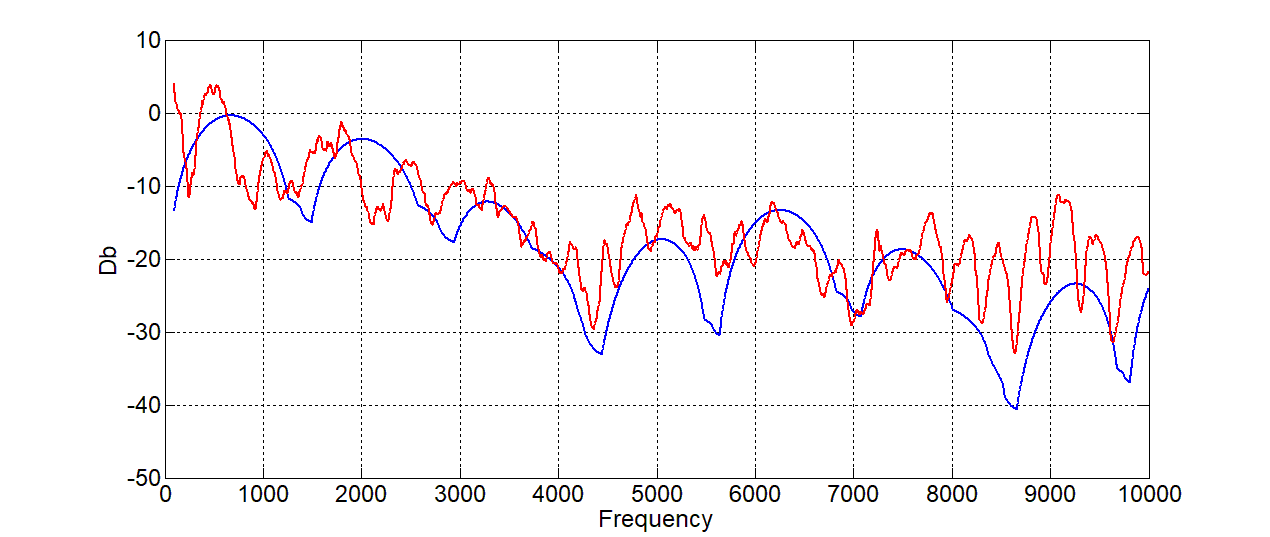
これはすぐには発生しなかったが、理論にローパスフィルターが適用されたと言う必要があります。 そして一般的に、いくつかの他の奇妙なものの影響が見えます。

他に何を比較できますか？

同じフェンダーを見てみましょう。 たとえば、ネック（150 mm）センサーとブリッジ（50 mm）センサーを比較することもできます。 最初の特性を測定し、2番目の特性を測定してから、別のグラフを調べます（少しフィルタリングした後）。



チャート上の緑は橋、オレンジは首です。 グラフから、誰もが知っているように見えるものを正確に見ることができます。 ネックは非常に低い周波数を引き出し、ブリッジはミッドハイです。 ここでの質問は、いつものように、音楽とこれすべての偉大な愛好家だけに興味がある詳細に生じます。 たとえば、ネックのピークは9000 Hz付近です。

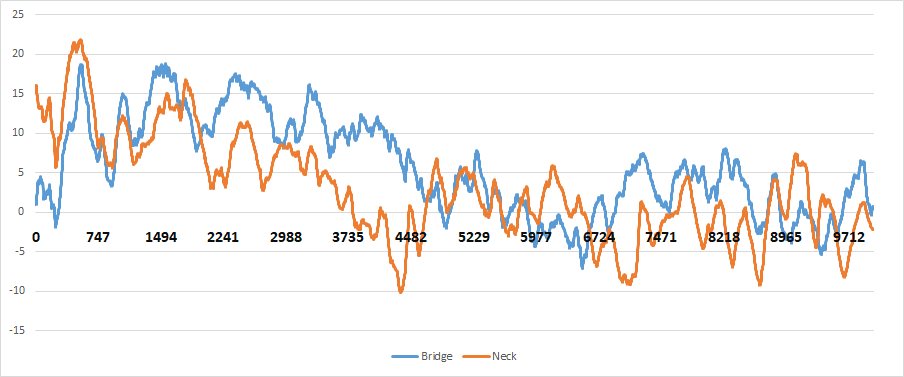
ご予約

では、 「実際、すべてがそれほど単純ではない」理由について。

マイク、特に指向性マイクも弦の一部のみを取ります。これは、マイクの位置とサウンドキャプチャの「幅」に応じて、センサーがそれぞれ同様の周波数応答を持っているためです。 ただし、マイクに「より広い」センサーがあることは明らかです。したがって、すべての正弦波周波数ははるかに大きく、マイクの周波数応答は、スペクトルで「ノイズを発生させる」高周波振動として主に表されます。



たとえば、センサーの首の位置を測定したFender Stratocaster Ritchie Blackmore Editionの周波数応答を考えてみましょう。 周波数応答は正弦で記述されているため（理論からわかるように）、割り当てられた周波数を推定するために再びスペクトルからフーリエ変換を行うことができます（ちなみに、スペクトルからフーリエを取得することは非常に疑わしい娯楽です）。 結果は写真に示されています。





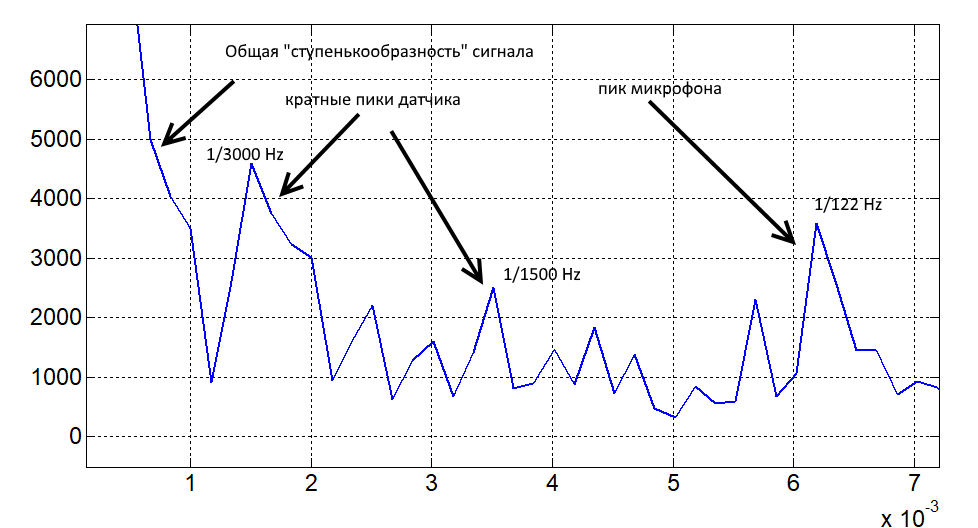
フーリエ変換スペクトラムフェンダーストラトキャスターリッチーブラックモア版（首）



「センサーの位置」、「センサーの幅」、および「マイクの幅」プロパティによって定義されるピークは明確に区別されます。 マイクがセンサーの真向かいにあるため、「マイク位置」のはっきりと区別できるピークがない可能性があります...

結論が好きな人のための結論

1. センサーの位置は、それ自体の周波数応答に影響します。 または多分さらに;
   
   
2. 式（3）に基づくセンサーの幅は、図に示されているとおりに影響します。
   
   

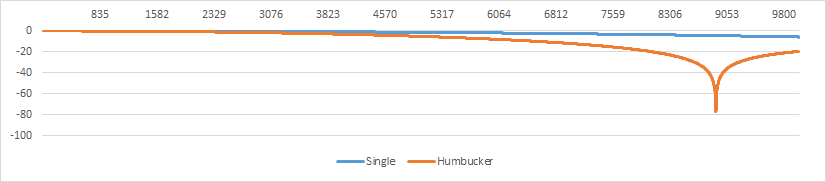
単一の場合、それはまったく影響しません。 ハムバッカーの場合、9000の領域で障害が発生するようにすべてが行われます。 そしてこれは、そのようなピックアップの企業の「明るくない」サウンドも形成します。 もちろん、このようなセンサーの音に影響を与えるのはこれだけではありません。

1. センサーを周波数を殺さないような方法で（または、幅を広げて）配置することは不可能です。 実際、これらの殺された周波数は、ギターの特徴的な音を設定します。
   
   
2. 注文したギターの特定のサウンドが必要な場合は、このサウンドを聞いた人を見つけることが重要です。そうすると、その楽器のセンサーの位置に焦点を当てやすくなります。
   
   
3. 原則として、センサーの位置、幅、電気回路の組み合わせからフィルターのいくつかを簡単に敢えて構築することができます。 これらのフィルターをマイクで録音されたいくつかのサウンドに適用し、視聴しますか？ ギターをそのように鳴らしたいですか？ そのような完璧なサウンドを探す準備はできていますか？
   
   

共著者： A.A. Gorodetsky、Imperial College London。



PS私たちはいくつかのrunetサイトに記事を公開しています。 VK 、 FB、または電報チャネルのページを購読して、すべての出版物およびその他のMaxilectニュースについて学びます。