算術級数の合計

一定数のセルを用意します。そのうちのいくつかは「ビジー」とマークできます。









占有されたセルの場所の選択肢がいくつあるかを調べる必要があります。

多くのタスクがこのスキームに帰着します。 たとえば、N + 1暦日の期間をl + 1連続するより小さい期間に分割します。 最適なオプションを選択するために、「ブルートフォース」法を使用して最適化計算を実行し、期間分割の可能性のある各バリアントの目的関数を計算するとします。 事前に計算時間を見積もるには、オプションの数を決定する必要があります。 これは、計算を開始するかどうかを決定するのに役立ちます。 同意する-プログラムのユーザーに、設定したパラメーターでは計算に10,000年かかることを事前に警告しておくと便利です。



任意のNとlが占有セルの位置のすべての可能なオプションの数を取得できるようにする簡単な式があります。

$$

$$S_l（n）= \ prod_ {i = 1} ^ l \ frac {n + i-1} {i}$$

$$

$$S_0（n）= 1$$

、ここでn = N-l + 1、n≠0。



これは、合計の合計の式です... 1 + 2 + 3 + ... + nの形式の算術的進行の合計。 このフレーズのさまざまな曲用の「合計」という単語は、l-1回だけ繰り返されます。 つまり、この式を使用すると、これらの金額をすばやく計算できます。

$$

$$S_l（n）= \ sum_ {i = 1} ^ nS_ {l-1}（i）$$

$$

$$S_0（n）= 1$$

通常のデスクトップPCでは、これらの金額を「正面から」計算するのに時間がかかりすぎます（特に長い計算を使用します-これなしではできません）。



この問題を解決し始めたばかりで（この式はまだ知りませんでした）、「算術的進行の合計」というフレーズを検索エンジンに記録しましたが、何も見つかりませんでした。 それがまさに私の記事と呼んでいるものです-この式の次の探求者がここですぐにそれを見つけることができると期待して。



この式に関する信頼できる情報源へのリンクはありません。 4000回以上のテストを実施し、分析的に推定し、数値的に確認しました。 興味がある場合は、記事の最後にその結論を示します。



算術の進行がセルレイアウトオプションのカウントにどのように関連するかをすぐに説明しますが、ここでは、より多くの既製の数式を紹介します。



追加の条件を導入します。どのシナリオでも、隣接する非占有セルのグループが少なくとも1つ存在する必要があるとします。 この場合、オプションの数は次のように決定されます。

$$

$$S_l ^ r（n）=（l + 1）\ cdot S_l（nr）-\ sum_ {j = 0} ^ {l-1} \ sum_ {i = r} ^ {nr-1} \ left [S_j ^ r（i + 1）\ cdot S_ {lj-1}（nri）\ right]$$

$$

$$S_l ^ r（n）= S_l（n）、\; \; \; \; \; \; \; n + l-1 \ geq r（l + 1）$$

$$

$$S_l ^ 0（n）= S_l（n）$$

$$

$$S_l ^ 1（n）= \ begin {cases} 0＆\ text {、for n = 1} \\ S_l（n）＆\ text {、for n> 1} \ end {cases}$$

$$

$$S_l ^ r（n）= 0、\; \; \; \; \; \; \; n \ leq r$$

$$

$$S_0 ^ r（n）= \ begin {cases} 1＆\ text {、for n> r} \\ 0＆\ text {、for n≤r} \ end {cases}$$

この式の結論は、記事の最後に続きます。



プログラムが各セルレイアウトオプションの計算を実行する場合、異なるオプションの計算はおそらく同じです。 これは、それらが複数のスレッドに簡単に分散されることを意味します。 この記事では、各スレッドが同じ数のオプションを取得できるように、オプションの繰り返しを整理する方法を説明します。

1.そして、進行はどこにありますか？

これが最も簡単な質問です。 セルの行の左端で、占有されているすべてのセルをグループ化します。つまり、行の左端のセルから順番にセルが続くようにします。









残りのセルがその場所に残っている場合、占有セルの右端の位置（最後に占有されたセルと呼びます）のオプションはいくつありますか？ 正確にn。 次に、PASTLAST-SIZED CELLを右に1ポジション移動します。 最後のセルにいくつのポジションが残っていますか？ n-1。最後から2番目のセルを右にn回シフトできます。 したがって、最後の2つの占有セルの場所には、S ₂ （n）= 1 + 2 + 3 + ... + nという非常に多くのオプションがあります。 3番目に占有されたセルを1ポジションだけ右に移動し、最後と最後から2番目のセルの場所のオプションの数を再度カウントします。 S ₂ （n-1）になります。 3番目のセルもn回だけ右にシフトでき、最後の3つのセルの合計ロケーションオプションはS ₃ （n）= S ₂ （1）+ S ₂ （2）+ ... + S ₂ （n）になります。



このように推論して、最終的にl個の占有セルすべての位置オプションの数に到達します。

$$

$$S_l（n）= \ sum_ {i = 1} ^ nS_ {l-1}（i）$$

$$

$$S_0（n）= 1$$

2.追加条件：r個の非占有隣接セルの少なくとも1つのグループ

まず、特殊なケースを検討します。 n + l-1≥r（l + 1）の場合、r個の未使用セルのグループが少なくとも1つあるバリアントはありません。 最悪の場合でも、行内の占有セルが均等に分布しているため、それらと行の端との間の距離がr-1である場合、占有セルの数はこれらの距離のすべてがr-1以下になるには不十分です。 1つは少なくともrに等しくなります。 したがって：

$$

$$S_l ^ r（n）= S_l（n）、\; \; \; \; \; \; \; n + l-1 \ geq r（l + 1）$$

r = 0は、セルの配置に満足していることを意味します。 この場合の条件「n + l-1≥r（l + 1）」は、nおよびlについて満たされます。

$$

$$S_l ^ 0（n）= S_l（n）$$

r = 1の場合、条件「n + l-1≥r（l + 1）」はn> 1の場合にのみ満たされます。

$$

$$S_l ^ 1（n）= \ begin {cases} 0＆\ text {、for n = 1} \\ S_l（n）＆\ text {、for n> 1} \ end {cases}$$

n≤rは、占有されていないセルの数がrより少ないことを意味し、隣接しているかどうかに関係なくrの占有されていないセルを取得する方法はありません。 したがって、前の式では、n = 1の場合に0がかかります。

$$

$$S_l ^ r（n）= 0、\; \; \; \; \; \; \; n \ leq r$$

占有されたセルがない場合、それらの場所には1つのオプションしかありません。

$$

$$S_0 ^ r（n）= \ begin {cases} 1＆\ text {、for n> r} \\ 0＆\ text {、for n≤r} \ end {cases}$$

今-他のすべてのケースのための一般化された式。



左端の占有セルを左端の位置に固定すると、他のすべてのセルのロケーションオプションはS ^r _（l-1） （n）になります。 右に1ポジション移動すると、オプションはS ^r _（l-1） （n-1）になります。 位置r + 1から開始して、行の左端に少なくともrのギャップが常にあるため、残りのオプションは再帰なしで計算できます：S _l （n-r）。 これは次のとおりです。

$$

$$S_l ^ r（n）= \ sum_ {i = 1} ^ {r} S_ {l-1} ^ r（n-i + 1）+ S_l（n-r）$$

式は正しいですが、私はこれを使用することを好みます：

$$

$$S_l ^ r（n）=（l + 1）\ cdot S_l（nr）-\ sum_ {j = 0} ^ {l-1} \ sum_ {i = r} ^ {nr-1} \ left [S_j ^ r（i + 1）\ cdot S_ {lj-1}（nri）\ right]$$

私の測定によると、それは前のものより10倍高速です。 それを導き出すことは難しくありませんが、長い間結論を述べることは困難です。 記事の終わりに私が伝えます。



これで、フロー全体に反復を分散させることができます。 これを理解するには、最初の式S ^r _l （n）がどのように導出されたかを明確に理解する必要があります。 この結論には、占有セルのロケーションオプションの特定の反復順序が含まれています。

3.複数のスレッドで反復を編成する方法

反復順序はすべてのスレッドに共通です。 最初は、すべてのl個のセルが行の左端にあり、位置1からlまでを占めます。 これが最初の反復です。 各反復での右端のセルは、行の最後になるまで1ポジション右にシフトされ、次にその左のセルは右に1ポジションシフトされ、極値セルは再びセルの左端と右端の間のすべての可能な位置を通過します。 両方のセルが右端の位置にある場合、それらの左のセルは右に1つ移動します。 すべてのセルが行の右端に来るまで続きます。 反復では、r個の隣接する非占有セルの単一グループがないオプションをスキップします。



この反復順序に従って、最初のkオプションを選択して最初のスレッドに割り当て、次に次のkオプションを2番目のスレッドに割り当てます。 n _t個のフローを使用することに決めたと仮定します。各フローの反復回数は、k _i 、i = 1、...、n _tとして決定します。



各ストリームの最初の反復のシーケンス番号はh _iと呼ばれます：

$$

$$h_i = 1 + \ sum_ {j = 1} ^ {i-1} k_j$$

番号がh _iのバリアントのセルの初期位置があれば、このバリアントからk _i回の反復を実行することは難しくありません（これがどのように行われるかは説明しません）。 ただし、オプションのシーケンス番号によって占有セルの位置を計算する関数が必要です。

using Anylong = boost::multiprecision::cpp_int; using Opt_UVec = boost::optional<std::vector<unsigned> >; Opt_UVec arrangement(Anylong index, unsigned n, unsigned l, unsigned r = 0);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

配置関数は、インデックスバリアント番号と行パラメーターを受け入れます。n= N-l + 1、lとr、-は、行内の占有セルの位置を含むベクトルを返します。 占有セル位置は、1〜Nの整数です。



オプションの数は、パラメータlおよびnの増加とともに非常に急速に増加するため、この数を表すには長い計算が必要です。 任意の長さの整数を表現できるboost :: multiprecision :: cpp_intクラスを使用しました。



インデックスパラメータが可能なセル位置の数を超える場合、関数は空のboost ::オプションオブジェクトを返します。 indexパラメーターまたはnパラメーターが0の場合、これはプログラマーエラーとして扱われ、関数は例外をスローします。



最初に、C ++数式に変換してオプションの数を決定します。

 struct Exception { enum class Code { INVALID_INPUT = 1 } code; Exception(Code c) : code(c) {} static Exception InvalidInput() { return Exception(Code::INVALID_INPUT); } }; Anylong S(unsigned n, unsigned l) { if (!n) throw Exception::InvalidInput(); if (l == 1) return n; if (n == 1 || l == 0) return 1; Anylong res = 1; for (unsigned i = 1; i <= l; ++i) { res = res * (n + i - 1) / i; //   ! } return res; } Anylong S(unsigned n, unsigned l, unsigned r) { if (!n) throw Exception::InvalidInput(); if (r == 0) return S(n, l); if (r == 1) if (n == 1) return 0; else return S(n, l); if (n + l - 1 >= r * (l + 1)) return S(n, l); if (n <= r) return 0; else if (l == 0) return 1; Anylong res = (l + 1) * S(n - r, l); for (unsigned j = 0; j <= l - 1; ++j) for (unsigned i = r; i <= n - r - 1; ++i) res -= S(i + 1, j, r) * S(n - r - i, l - j - 1); return res; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この行に注意してください：

  res = res * (n + i - 1) / i;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここでは手順が重要です。 因子resと（n + i-1）の積は、 常に完全にiで除算されますが、それぞれは個別に除算されません。 手順に違反すると、結果に歪みが生じます。



さて、100件の質問、インデックスによるロケーションオプションの決定方法。



採用した反復順序を思い出してください。 左端のセル1の位置を右にシフトするには、X ₁ = S ^r _l-1 （n）回の反復が必要です。 X ₂ = S ^r _l-1 （n-1）回の繰り返しで、さらに1セル分右に移動できます。 ある時点でX ₁ + X ₂ + ... + X _i + X _{i + 1}がインデックスよりも大きいことが判明した場合、最初に占有されたセルの位置を決定しました。 i番目の位置にあるはずです。 次に、2番目のセルを右に移動するために必要な反復回数を計算します：X ₁ = S ^r _l-2 （n-i + 1）。 これは、オプション番号のインデックスに到達するまで続きます。 少なくとも1回iがrより大きい場合、現在のセルの左側に少なくともrのギャップが少なくとも1つあるため、S ^r _l （n）へのすべての後続の呼び出しはS _l （n）に置き換えられます。



言葉で説明するよりもコードを書く方が短くなります。

 Opt_UVec arrangement(Anylong index, unsigned n, unsigned l, unsigned r = 0) { if (index == 0) throw Exception::InvalidInput(); if (index > S(n, l, r)) return {}; std::vector<unsigned> oci(l); /* occupied cells indices -      (  1  N) */ if (l == 0) return oci; if (l == 1) { assert(index <= std::numeric_limits<unsigned>::max()); oci[0] = (unsigned)index; return oci; } oci[0] = 1; unsigned N = n + l - 1; unsigned prev = 1; Anylong i = 0; auto it = oci.begin(); while (true) { auto s = S(n, --l, r); while (i + s <= index) { if ((i += s) == index) { auto it1 = --oci.end(); if (it1 == it) return oci; *it1 = N; for (it1--; it1 != it; it1--) *it1 = *(it1 + 1) - 1; return oci; } s = S(--n, l, r); assert(n); (*it)++; if (r && (*it) > prev + r - 1) r = 0; } prev = *it++; assert(it != oci.end()); *it = prev + 1; } assert(false); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

4.式の導出

学校代数のファンを別のセクションで喜ばせます。



算術級数の合計から始めましょう：

$$

$$S_l（n）= \ sum_ {i = 1} ^ nS_ {l-1}（i）$$

$$

$$S_0（n）= 1$$

ご覧のとおり、l = 0の場合、S ₀ （n）= 1は次数0の多項式です。 l = 1の場合、S ₁ （n）= nは1次の多項式です。 l = 2の場合、算術級数S ₂ （n）= n（n + 1）/ 2の合計の公式が使用されます。 そして、これは2次の多項式です。 l = 3の場合、次数3の多項式になると仮定できます。 n = 1、2、3、および4のS ₃ （n）の値を手動で計算し、線形方程式系を構成し、この多項式の係数を見つけます。 結果を因数分解してこれを取得します。

$$

$$S_3（n）= \ frac {n（n + 1）（n + 2）} {6}$$

ここには明らかなパターンがあります。 次の式を書きます。

$$

$$S_l（n）= \ prod_ {i = 1} ^ l \ frac {n + i-1} {i}$$

l = 3についてはまだ証明されていませんが、l = 1およびl = 2についてはすでに証明されています。数学的帰納法を使用します。 式S _l-1 （n）が任意のnについて真であると仮定し、この場合、式S _l （n）も真であることを証明します。

$$

$$S_l（n）= S_ {l-1}（n）+ S_ {l-1}（n-1）+ ... + S_ {l-1}（1）= \ prod_ {i = 1} ^ {l} \ frac {n + i-1} {i}$$

マットの方法を適用します。 繰り返しますが、lではなくパラメータnに関してです。 式がn = 1に対して有効であることは明らかです。n-1に対して有効であるとします。

$$

$$S_l（n-1）= S_ {l-1}（n-1）+ S_ {l-1}（n-2）+ ... + S_ {l-1}（1）= \ prod_ {i = 1} ^ {l} \ frac {n + i-2} {i}$$

前の式からこれを引きます：

$$

$$S_ {l-1}（n）= \ frac {\ prod_ {i = 1} ^ {l}（n + i-1）} {l！}-\ frac {\ prod_ {i = 0} ^ { l-1}（n + i-1）} {l！}$$

$$

$$S_ {l-1}（n）= \ left [\ prod_ {i = 1} ^ {l-1} \ frac {n + i-1} {i} \ right] \ times \ frac {（n + l-1）-（n + 0-1）} {l}$$

$$

$$S_ {l-1}（n）= \ prod_ {i = 1} ^ {l-1} \ frac {n + i-1} {i}$$

結果は真のアイデンティティです。



r≠0のオプションを計算する式に戻ります。

$$

$$S_l ^ r（n）=（l + 1）\ cdot S_l（nr）-\ sum_ {j = 0} ^ {l-1} \ sum_ {i = r} ^ {nr-1} \ left [S_j ^ r（i + 1）\ cdot S_ {lj-1}（nri）\ right]$$

以下のように表示されます。



最後に占有されたセルと行の右端との間のギャップがr以上の場合、オプションの数を計算します。 最後の占有セルのサイズがr + 1に成長したように見えますが、行の寸法は同じままです。











このオプションの数は、S _l （n-r）と同じです。



次に、最後の占有セルと最後から2番目の占有セルの間のギャップがr以上であるオプションの数を追加します。 このオプションの数は再びS _l （n-r）に等しくなります。 しかし、以前のS _l （n-r）を計算したときに、これらのオプションのいくつかを既に数えていました。 つまり、最後に占有されたセルと行の右端の間のギャップがr以上であるバリアント。 したがって、最初のS _l （n-r）オプションには、S _l （n-r）ではなく、S _l （n-r）-Xを追加する必要があります。Xは、最後のセルと最後から2番目の占有セルのギャップが大きいオプションの数ですまたは、rに等しく、最後に占有されたセルと行の右端との間のギャップ。



j番目に占有されているセルごとにまったく同じことを行う必要があります-S _l （n-r）から、j番目のセルとその左側のセルとのギャップ（左端のセルの場合-それと行の左端との間のギャップ、およびj番目のセルの右側の少なくとも1つのギャップはr以上です。



合計で、占有セル間にl-1個のギャップがあり、さらにビジーセルと行の終わりに2個のギャップがあります。 したがって、S _l （n-r）という用語は、式l + 1回に含まれます。 ただし、X _jは 、右端の占有セルと行の右端の間のギャップについては計算されません。 したがって、これらの用語はlのみになります。

$$

$$S_l ^ r（n）=（l + 1）S_l（n-r）-\ sum_ {j = 0} ^ {l-1} X_j$$

jの範囲は0〜l-1です。このようなインデックスの順序は既に採用しています。 次に、j番目のセルの右側にある占有セルの数はjです。



この写真を見てください：









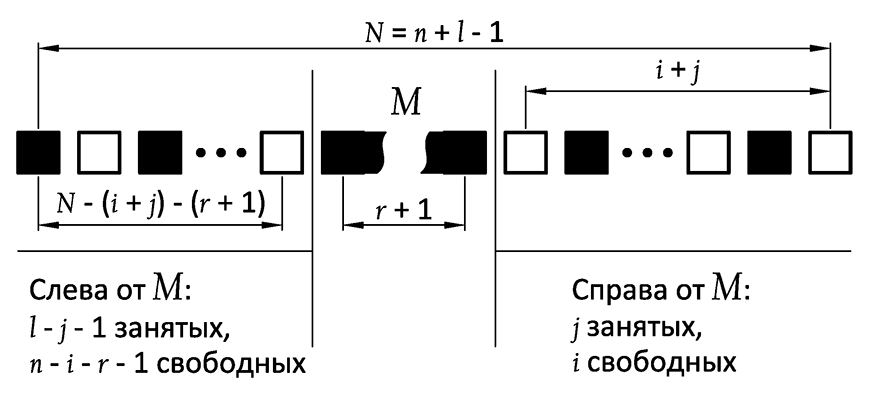
j番目のセル（jを反復するときにサイズr + 1に成長するセル）はMと表示されます。n-rの可能な位置にあり、パラメータiによって決定されます（i∈[0、n-r-1]） 。 i <rの場合、Mの右側のすべての間隔はrより小さいため、最初のr位置は考慮できません。 したがって、i∈[r、n-r-1]。



少なくとも1つのギャップがr以上であるMの右側のセル位置オプションの数は、S ^r _j （i + 1）です。 Mの左側のセル位置オプションの数は、S _l-j-1 （n-i-r）です。 合計で、すべてのi∈[r、n-r-1]およびすべてのj∈[0、l-1]についてS ^r _j （i + 1） ∙ S _l-j-1 （n-i-r）を取得します。

$$

$$S_l ^ r（n）=（l + 1）\ cdot S_l（nr）-\ sum_ {j = 0} ^ {l-1} \ sum_ {i = r} ^ {nr-1} \ left [S_j ^ r（i + 1）\ cdot S_ {lj-1}（nri）\ right]$$

これが私たちの公式です。