たたみ込みニューラルネットワークトレーニング
初期段階では、ニューラルネットワークは訓練されていません（構成されていません）。 一般的な意味では、学習は、トレーニングセットからニューラルネットワークの入力への画像の連続的な提示として理解され、受信された回答は目的の出力と比較されます。この場合、1-画像は顔を表し、-1-画像は背景（顔ではない）を表し、予想される差回答と受信は、エラー関数の結果（エラーデルタ）です。 次に、このエラーデルタをネットワーク内のすべての接続ニューロンに伝播する必要があります。
したがって、ニューラルネットワークのトレーニングは、ニューロン間のシナプス接続の重み係数を調整することにより、誤差関数を最小化するために削減されます。 エラー関数は、受信した回答と目的の回答の違いとして理解されます。 たとえば、顔画像が入力に送信され、ニューラルネットワークの出力が0.73であり、望ましい結果が1（顔画像のため）であると仮定すると、ネットワークエラーは差、つまり0.27であることがわかります。 次に、ニューロンの出力層の重みがエラーに応じて調整されます。 出力層ニューロンの場合、実際の出力値と目的の出力値は既知です。 したがって、そのようなニューロンの結合重みの設定は比較的簡単です。 ただし、前の層のニューロンの場合、設定はそれほど明確ではありません。 長い間、隠れ層にエラーを拡散するための既知のアルゴリズムはありませんでした。
エラー伝播アルゴリズム
記述されたニューラルネットワークをトレーニングするために、逆伝播アルゴリズムが使用されました。 多層ニューラルネットワークをトレーニングするこの方法は、一般化デルタルールと呼ばれます。 この方法は、1986年にRumelhart、McClelland、およびWilliamsによって提案されました。 これは、70年代初頭に衰退し始めたニューラルネットワークへの関心の復活を示しました。 このアルゴリズムは、多層ニューラルネットワークのトレーニングに実際に適用できる最初で主要なものです。
出力層の場合、重みの調整は直感的ですが、隠れ層の場合、アルゴリズムは長い間知られていませんでした。 非表示のニューロンの重みは、特定のニューロンが関連付けられているニューロンのエラーに正比例して変化する必要があります。 そのため、ネットワークを介したこれらのエラーの逆伝播により、すべてのレイヤー間の結合の重みを正しく構成できます。 この場合、エラー関数の大きさが減少し、ネットワークが学習します。
エラーの逆伝播法の主な関係は、次の表記法で取得されます。
エラー値は、式2.8の二乗平均平方根誤差によって決定されます。
画像pの各ニューロンjの非アクティブ状態は、式2.9に従って加重和として書き込まれます。
各ニューロンjの出力は、活性化関数の値です
これにより、ニューロンが活性化状態になります。 活性化関数として、連続微分可能な単調関数を使用できます。 ニューロンの活性化状態は、式2.10によって計算されます。
勾配降下法は、誤差を最小化する方法として使用されます;この方法の本質は、勾配ベクトルに沿った動きによる関数の最小（または最大）を見つけることです。 最小値を見つけるには、動きが反勾配の方向にある必要があります。 図2.7に従った勾配降下法。
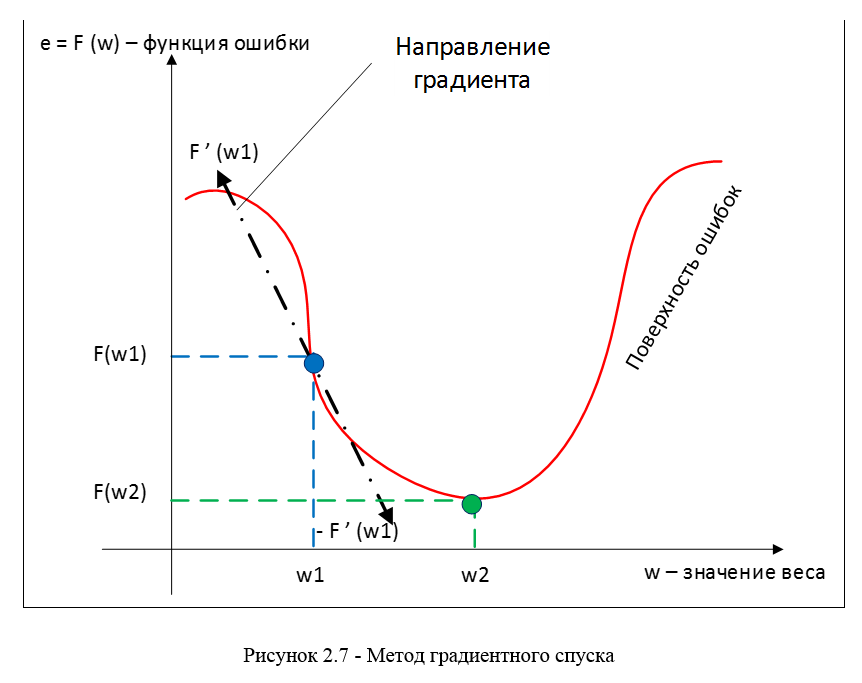
損失関数の勾配は、式2.11で計算される偏微分ベクトルです。
特定の画像の誤差関数の導関数は、チェーンルール、式2.12に従って記述できます。
ニューロンエラー
通常、δ（デルタ）として記述されます。 出力層の場合、エラーは明示的に定義されます。式2.8の導関数を使用すると、 tマイナスy 、つまり目的の出力と結果の出力の差が得られます。 しかし、非表示レイヤーのエラーを計算する方法は？ この問題を解決するために、エラーの逆伝播アルゴリズムが発明されました。 その本質は、出力レイヤーのエラー値を使用して、隠れレイヤーのエラーを順次計算することです。 エラー値は、出力から入力へと反対方向にネットワーク全体に伝播します。
隠れ層の誤差δは、式2.13によって計算されます。
エラー伝播アルゴリズムは、次の手順に縮小されます。
- ネットワークを介した直接信号伝搬、ニューロンの状態の計算。
- 出力層のエラー値δの計算。
- バックプロパゲーション：すべての隠されたレイヤーの最後から最初まで順番に、式2.13でδを計算します。
- ネットワークの重みを以前に計算されたδエラーに更新します。
多層パーセプトロンの逆伝播アルゴリズムを以下に示します。
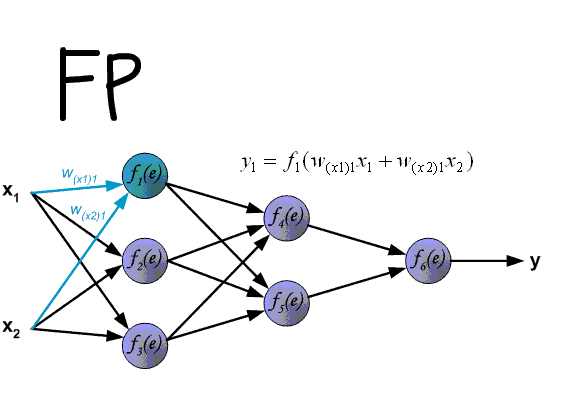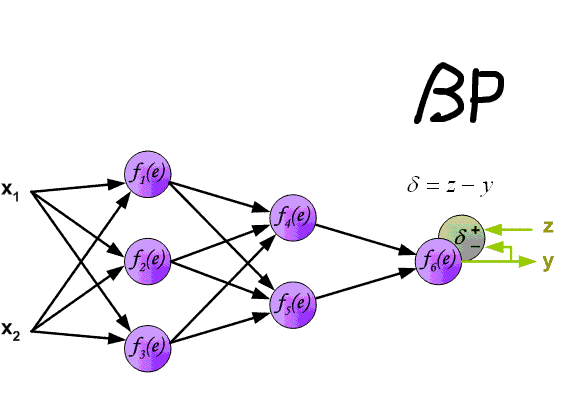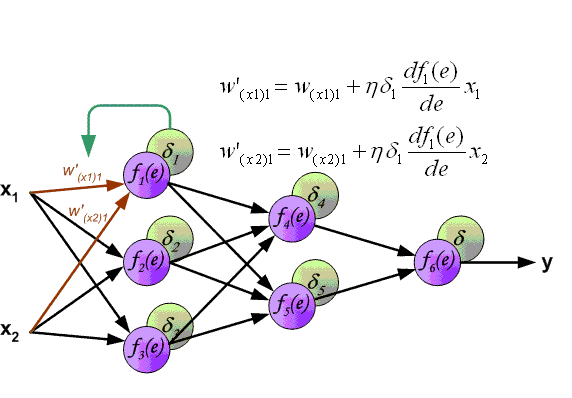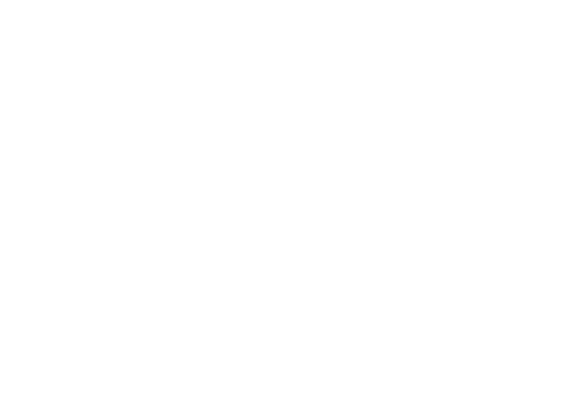
これまで、パーセプトロン層を介した、つまり出力に沿った隠れたエラー伝搬のケースが検討されてきましたが、それらに加えて、畳み込みニューラルネットワークにはサブサンプルと畳み込みがあります。
サブサンプルレイヤーの誤差の計算
サブサンプルレイヤーのエラーの計算は、いくつかの方法で表示されます。 最初のケースでは、サブサンプル層が完全に接続された層の前にある場合、それはそれぞれ完全に接続された層と同じタイプのニューロンと接続を持ち、δ誤差の計算はδ隠れ層の計算と変わりません。 2番目の場合、サブサンプル層が畳み込み層の前にある場合、δの計算は逆畳み込みによって行われます。 コンボリューションバックを理解するには、まず通常のコンボリューションと、フィーチャマップ上のスライディングウィンドウ（直接信号伝搬中）がニューロン間の接続を持つ通常の隠れ層として解釈できることを理解する必要がありますが、主な違いはこれらの接続が分離可能であることです。つまり、1つだけでなく複数のニューロンのペアが特定の重み値を持つ1つの接続を持つことができます。 図2.8による通常の多層形式での畳み込み演算の解釈。
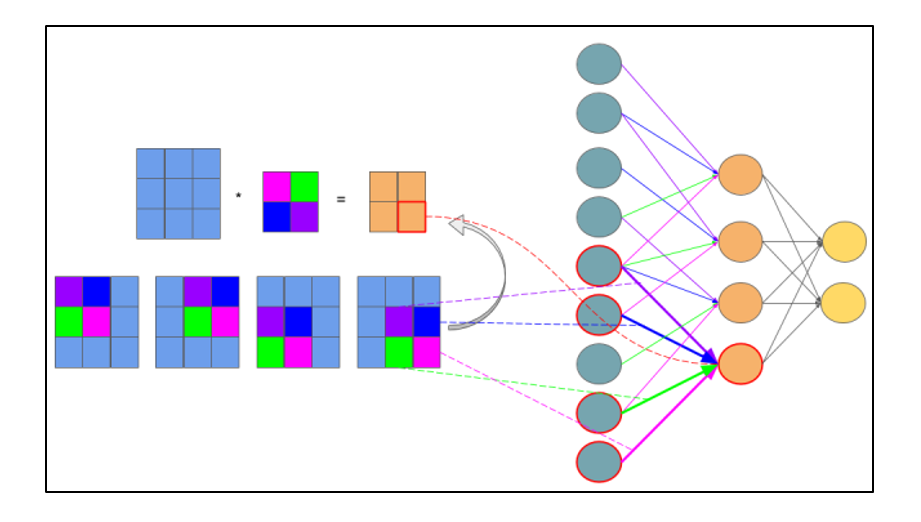
図2.8-同じ色の関係の重みが同じである多層形式での畳み込み演算の解釈。 サブサンプルマップは青で、シナプスコアは多色で、結果の畳み込みはオレンジで示されます。
畳み込み演算が通常のマルチレイヤー形式で表示されるようになったため、デルタの計算が完全に接続されたネットワークの隠れ層と同じ方法で行われることを直感的に理解できます。 したがって、畳み込み層のデルタを事前に計算しておくと、図2.9に従ってサブサンプルデルタを計算できます。
図2.9-δ畳み込み層とコアによるδサブサンプル層の計算
逆たたみ込みは、わずかにトリッキーな方法でのみデルタを計算する同じ方法で、コアを180度回転させ、修正されたエッジ効果でデルタのたたみ込みマップをスキャンするスライディングプロセスで構成されます。 簡単に言えば、（サブサンプルレイヤーに続く）畳み込みカードのコアを取得して180度回転し、以前に計算された畳み込みデルタを使用して通常の畳み込みを行う必要がありますが、スキャンウィンドウはマップを超えます。 図2.10に従った逆たたみ込み演算の結果、図2.11に従った逆たたみ込みのパスサイクル
図2.10-逆畳み込み演算の結果
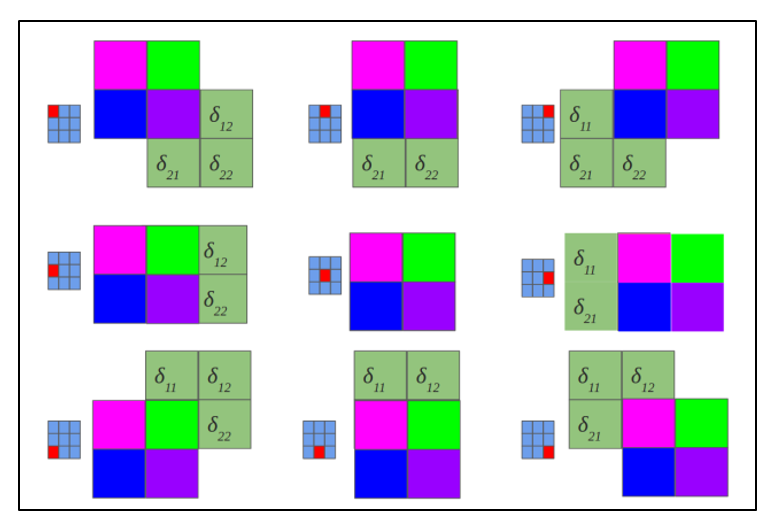
図2.11-180度回転したコアが畳み込みカードをスキャンする
畳み込み誤差の計算
通常、畳み込み層の後の先頭の層はサブサンプルであるため、サブサンプル層のデルタに関する知識により、現在の層のデルタ（畳み込み）を計算することがタスクです。 実際、デルタエラーは計算されず、コピーされます。 直接信号伝播では、サブサンプル層ニューロンは、最大値を持つニューロンが選択された畳み込み層に沿った非重複スキャンウィンドウにより形成され、逆伝播では、誤差デルタを以前に選択された最大ニューロンに返し、残りはゼロ誤差デルタを受け取ります。
おわりに
コンボリューション操作を通常のマルチレイヤー形式（図2.8）で示したので、デルタの計算は完全に接続されたネットワークの隠れ層と同じ方法で行われることを直感的に理解できます。
ソース
畳み込みニューラルネットワークのエラー伝播アルゴリズム
畳み込み層でのエラー伝播
1と2
パーセプトロン逆伝播
RSLでマカレンコの論文を読むことができます：アルゴリズムと分類ソフトウェア