はじめに
1934年、Stodolaの理論的研究に基づいたスイスの企業Brown-Boveriは、84％の効率で多段軸流圧縮機を最初に作成しました。 まもなく、この会社は軸流コンプレッサーをガスタービンプラントに使用することに成功しました。
多段軸流コンプレッサー[1]
アキシャル多段圧縮機の概略図を図に示します：
軸方向多段圧縮機は、ハウジング7に連続して取り付けられた一連のガイドベーン6と、ドラムローター11に配置されたローターブレード5で構成されます。
回転することにより、ローターブレードは運動エネルギーをガスに与えます。 作業ブレードの膨張チャネルに沿って移動すると、相対空気速度が低下し、流れの運動エネルギーが減少し、それに応じて圧力が増加します。
作動中のブレードのチャネル内の相対流量の変化は、コンプレッサーに供給されるエネルギーの消費に関連しています。
ガイドベーンの拡大チャネルでは、空気圧のさらなる増加とその移動速度の減少が観察されます。 空気は、入口パイプ１およびガイド装置４を通って圧縮機の流れ部分に入り、そこから、作動ブレード５およびガイドブレード６のチャネルを通過した後、矯正装置８に入る。
誘導装置は、第１段階に入る前に空気流の必要な方向を提供し、矯正装置は、ディフューザ９に、そして次に出力パイプ１０に軸方向出力を提供する。
この設計における圧縮段の数は、ドラムローター11にある作動ブレード5の数によって決まります。
多段レシプロコンプレッサー[2]
高圧（0.1〜2 MPa以上）の圧縮ガスを得るには、各段階の後に中間ガス冷却を備えた多段圧縮機を使用します。
多段圧縮の本質は、2段圧縮機の例で説明できます。そのスキームと理想的な（Vo = 0の）インジケータ図を図に示します。
第1段階1では、ガスはポリトロープ1-2に沿って圧力P2まで圧縮され、中間冷却器3に入り、そこで初期温度T1まで冷却されます。 空気経路を通る冷蔵庫の油圧抵抗が小さくなります。 これにより、2〜3等圧の冷却プロセスを検討できます。
冷蔵庫の後、ガスは第2ステージ2に入り、そこでポリトロープ3-4に沿って圧力P3に圧縮されます。 圧力P3への圧縮が理想的な1段圧縮機で実行された場合（ライン1〜2 '）、サイクルごとに費やされる作業量は、エリア012'b0によって決まります。
中間冷却による2段階圧縮では、この仕事は01234b0の面積に等しくなります。 ハッチングされた領域は、2段階圧縮でサイクルごとの作業を節約することに対応しています。
多段ガス圧縮[3]
初期圧力Poから最終圧力Pnまでのガスの多段階等エントロピー圧縮では、圧縮で消費される全エネルギーが最小になるような中間圧力を確立することが望ましい。
断熱圧縮が行われるたびに、気体はその初期温度Tに等圧に冷却されます。 n段階でのエネルギーコストは、次の式から決定されます。
ここで、mは圧縮性ガスのキロモル数、Rはユニバーサルガス定数、
;
Tは初期ガス温度Kです。 γは、一定の圧力と一定の体積でのガスの比熱容量の比であり、作業では、γ= 1.4。 xnは、n段階での圧縮後のガス圧です。
問題の声明
1.断熱圧縮段の出口でそのような圧力分布を見つける
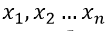圧縮で消費されたエネルギー 
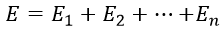最小限になります。
2.同じ初期圧力と最終圧力での最小圧縮エネルギーに対する圧縮比の数の効果を決定する。
scipyライブラリを使用した問題の解決策。 最適化する
最初に、図に示されている設計スキームに従って5段階の圧縮を検討します。
プログラムリスト
#!/usr/bin/env python #coding=utf8 import numpy as np# from scipy.optimize import minimize# import matplotlib.pyplot as plt# import time# Po=1# Pzad=64# g=1.4# m=10# R=8.314# a=(g-1)/g T=293# a=0.286 " :" def E1(x1): return m*R*T*a*((x1/Po)**2-1) def E2(x1,x2): return m*R*T*a*((x2/x1)**2-1) def E3(x2,x3): return m*R*T*a*((x3/x2)**2-1) def E4(x3,x4): return m*R*T*a*((x4/x3)**2-1) def E5(x4): return m*R*T*a*((Pzad/x4)**2-1) start = time.time() def E(x1,x2,x3,x4):# return E1(x1)+E2(x1,x2)+E3(x2,x3)+E4(x3,x4)+E5(x4) def fun2(x): return E(*x) x0 =[4,15,24,40] # res = minimize(fun2, x0)# stop = time.time() print (" :",round(stop-start,3)) x1=round(res['x'][0],3)# I x2=round(res['x'][1],3)# II x3=round(res['x'][2],3)# III x4=round(res['x'][3],3)# IV x5=Pzad " :" x=[] x.append(x1) x.append(x2) x.append(x3) x.append(x4) x.append(x5) z1=E1(x1)# I z2=E2(x1,x2)+z1# I+II z3=E3(x2,x3)+z2# I+II +III z4=E4(x3,x4)+z3# I+II +III +IV z5=E5(x4)+z4# I+II +III +IV+V " :" y=[] y.append(z1) y.append(z2) y.append(z3) y.append(z4) y.append(z5) plt.title(' - %s %s \n\ %s %s '%(int(z5),len(y),Po,Pzad)) plt.ylabel(' ') plt.xlabel(' ') plt.plot(x[0],y[0],'o', label='I , - %s'%x1) plt.plot(x[1],y[1],'o', label='II , - %s'%x2) plt.plot(x[2],y[2],'o', label='III , - %s'%x3) plt.plot(x[3],y[3],'o', label='IV , - %s'%x4) plt.plot(x[4],y[4],'o', label='V , - %s'%x5) plt.plot(x,y,'r') plt.legend(loc='best') plt.grid(True) plt.show()
取得するもの：
オプティマイザーの実行時間：0.0
次のリストに従って、圧縮ステップの数を1つ増やします。
プログラムリスト
#!/usr/bin/env python #coding=utf8 import numpy as np# from scipy.optimize import minimize# import matplotlib.pyplot as plt# import time# Po=1# Pzad=64# g=1.4# m=10# R=8.314# a=(g-1)/g T=293# a=0.286 " :" def E1(x1): return m*R*T*a*((x1/Po)**2-1) def E2(x1,x2): return m*R*T*a*((x2/x1)**2-1) def E3(x2,x3): return m*R*T*a*((x3/x2)**2-1) def E4(x3,x4): return m*R*T*a*((x4/x3)**2-1) def E5(x4,x5): return m*R*T*a*((x5/x4)**2-1) def E6(x5): return m*R*T*a*((Pzad/x5)**2-1) start = time.time() def E(x1,x2,x3,x4,x5): return E1(x1)+E2(x1,x2)+E3(x2,x3)+E4(x3,x4)+E5(x4,x5)+E6(x5) def fun2(x): return E(*x) x0 =[4,15,20,30,40]# res = minimize(fun2, x0)# stop = time.time() print (" :",round(stop-start,3)) x1=round(res['x'][0],3)# I x2=round(res['x'][1],3)# II x3=round(res['x'][2],3)# III x4=round(res['x'][3],3)# IV x5=round(res['x'][4],3)# V x6=Pzad# VI " :" x=[] x.append(x1) x.append(x2) x.append(x3) x.append(x4) x.append(x5) x.append(x6) z1=E1(x1)# I z2=E2(x1,x2)+z1# I+II z3=E3(x2,x3)+z2# I+II+III z4=E4(x3,x4)+z3# I+II+III+IV z5=E5(x4,x5)+z4# I+II+III+IV+V z6=E6(x5)+z5# I+II+III+IV+V +VI " :" y=[] y.append(z1) y.append(z2) y.append(z3) y.append(z4) y.append(z5) y.append(z6) plt.title(' - %s %s \n\ %s %s '%(int(z6),len(y),Po,Pzad)) plt.ylabel(' ') plt.xlabel(' ') plt.plot(x[0],y[0],'o', label='I , - %s'%x1) plt.plot(x[1],y[1],'o', label='II , - %s'%x2) plt.plot(x[2],y[2],'o', label='III , - %s'%x3) plt.plot(x[3],y[3],'o', label='IV , - %s'%x4) plt.plot(x[4],y[4],'o', label='V , - %s'%x5) plt.plot(x[5],y[5],'o', label='VI , - %s'%x6) plt.plot(x,y,'r') plt.legend(loc='best') plt.grid(True) plt.show()
取得するもの：
オプティマイザーランタイム：0.005
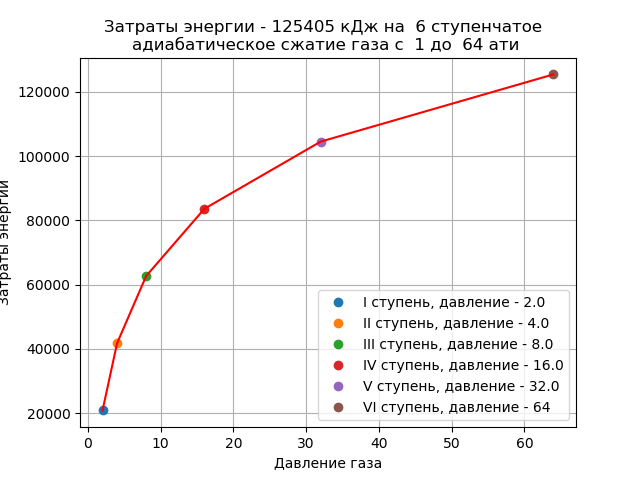
これらのグラフを比較すると、断熱ガス圧縮のエネルギー消費の削減を判断できます。
（149024 -125405）* 100/149024 = 15、85％
結論：圧縮段数を1ユニットだけ増やすと、多段圧縮機での断熱ガス圧縮に費やされるエネルギーのほぼ16％を節約できます。
ただし、これは消費されるエネルギーの1つのタイプにすぎません。 追加のステージを導入すると、製造コストが増加するだけでなく、エンジン出力と冷却システムのセクションが増加するため、運用コストも増加することは明らかです。
あらゆる種類のコストを考慮して最適なオプションを選択する必要がありますが、これはまったく別のタスクです。
結論：
1.断熱圧縮段の出口での圧力分布が見つかりました
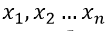断熱圧縮で消費されるエネルギー 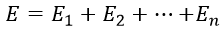最小限です。
2. 1ユニットだけ圧縮ステップ数を増やすと、多段圧縮機での断熱ガス圧縮に費やされるエネルギーのほぼ16％を節約できます。
参照：
1. ガスタービンユニット（GTU）のコンプレッサー。
2. 多段コンプレッサー。
3.ファン-リエン-セン、ワン、チュー-セン。 離散最大原理。 -M、ミール、1967.-176 p。